轮转数组[中等]
优质博文:IT-BLOG-CN
一、题目
给定一个整数数组nums,将数组中的元素向右轮转k个位置,其中k是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105
进阶: 尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。你可以使用空间复杂度为O(1)的原地算法解决这个问题。
二、代码
【1】使用额外的数组: 我们可以使用额外的数组来将每个元素放至正确的位置。我们遍历原数组,将原数组下标为i的元素放至新数组下标为(i+k) mod nums.length的位置,最后将新数组拷贝至原数组即可。
class Solution {public void rotate(int[] nums, int k) {// 使用一个等长的数组int[] newArray = new int[nums.length];for (int i = 0; i < nums.length; i++) {newArray[(i + k) % nums.length] = nums[i];}System.arraycopy(newArray, 0, nums, 0, nums.length);}
}
时间复杂度: O(n)其中n为数组的长度。
空间复杂度: O(n)
【2】数组翻转: 该方法基于如下的事实:当我们将数组的元素向右移动k次后,尾部k mod n个元素会移动至数组头部,其余元素向后移动k mod n个位置。
该方法为数组的翻转: 我们可以先将所有元素翻转,这样尾部的k mod n个元素就被移至数组头部,然后我们再翻转[0,k mod n−1]区间的元素和[k mod n,n−1]区间的元素即能得到最后的答案。
我们以n=7,k=3为例进行如下展示:
| 操作 | 结果 |
|---|---|
| 原始数组 | 1 2 3 4 5 6 7 |
| 翻转所有元素 | 7 6 5 4 3 2 1 |
翻转[0,k mod n−1]区间的元素 | 5 6 7 4 3 2 1 |
翻转 [k mod n,n−1]区间的元素 | 5 6 7 1 2 3 4 |
class Solution {public void rotate(int[] nums, int k) {// 放置下表越界k %= nums.length;// 数组反转reverse(nums, 0 , nums.length - 1);reverse(nums, 0, k - 1);reverse(nums, k, nums.length - 1);}private void reverse(int[] nums, int start, int end) {while(start < end) {int temp = nums[start];nums[start] = nums[end];nums[end] = temp;++start;--end;}}
}
【3】环状替换: 方法一中使用额外数组的原因在于如果我们直接将每个数字放至它最后的位置,这样被放置位置的元素会被覆盖从而丢失。因此,从另一个角度,我们可以将被替换的元素保存在变量temp中,从而避免了额外数组的开销。
我们从位置0开始,最初令temp=nums[0]。根据规则,位置0的元素会放至(0+k) mod n的位置,令x=(0+k) mod n,此时交换temp和nums[x],完成位置x的更新。然后,我们考察位置x,并交换temp和nums[(x+k) mod n],从而完成下一个位置的更新。不断进行上述过程,直至回到初始位置0。
容易发现,当回到初始位置0时,有些数字可能还没有遍历到,此时我们应该从下一个数字开始重复的过程,可是这个时候怎么才算遍历结束呢?我们不妨先考虑这样一个问题:从0开始不断遍历,最终回到起点0的过程中,我们遍历了多少个元素?由于最终回到了起点,故该过程恰好走了整数数量的圈,不妨设为a圈;再设该过程总共遍历了b个元素。因此,我们有an=bk,即an一定为n,k的公倍数。又因为我们在第一次回到起点时就结束,因此a要尽可能小,故an就是n,k的最小公倍数lcm(n,k),因此b就为lcm(n,k)/k。
这说明单次遍历会访问到lcm(n,k)/k个元素。为了访问到所有的元素,我们需要进行遍历的次数为n/(lcm(n,k)/k)=nk/(lcm(n,k))=gcd(n,k)
其中
gcd指的是最大公约数。
我们用下面的例子更具体地说明这个过程:
nums = [1, 2, 3, 4, 5, 6]
k = 2
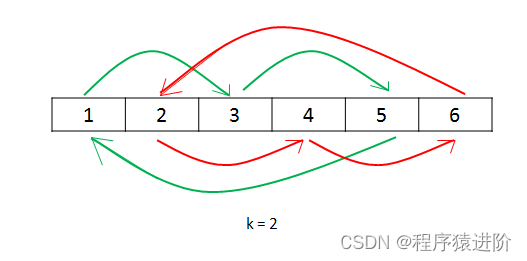
如果读者对上面的数学推导的理解有一定困难,也可以使用另外一种方式完成代码:使用单独的变量count跟踪当前已经访问的元素数量,当count=n时,结束遍历过程。
class Solution {public void rotate(int[] nums, int k) {int n = nums.length;k = k % n;int count = gcd(k, n);for (int start = 0; start < count; ++start) {int current = start;int prev = nums[start];do {int next = (current + k) % n;int temp = nums[next];nums[next] = prev;prev = temp;current = next;} while (start != current);}}public int gcd(int x, int y) {return y > 0 ? gcd(y, x % y) : x;}
}
时间复杂度: O(n)其中n为数组的长度。每个元素只会被遍历一次。
空间复杂度: O(1)我们只需常数空间存放若干变量。
相关文章:

轮转数组[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个整数数组nums,将数组中的元素向右轮转k个位置,其中k是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,…...
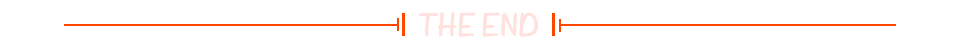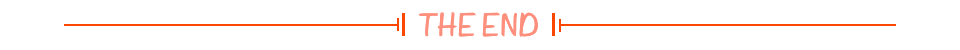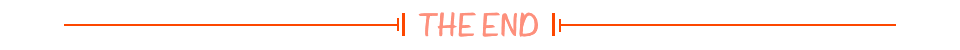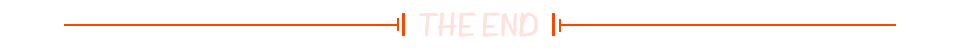
【SpringBoot系列】自动装配的魅力:Spring Boot vs 传统Spring
IT行业有哪些证书含金量高? 文章目录 IT行业有哪些证书含金量高?强烈推荐前言区别项目配置:依赖管理:内嵌服务器:开发体验: 实例Spring项目示例:Spring Boot项目示例: 总结强烈推荐专栏集锦写在最后 强烈…...

idea自动生成实体类
第一步:idea连接数据库 出现这个就连接成功 第二步:选择数据库 第三步:创建实体类 也可以点击数据库一下子全部创建 选择创建实体类所放位置 这样就完成了,点击看看对其做相应修改...

uniapp -- picker民族选择器
目录 一、实现思路 二、实现步骤 ①view部分展示 ② JavaScript 内容 ③css中样式展示 三、效果展示...
)
生信学习笔记1:学习如何用OPLS-DA分析代谢组数据(从入门到掌握)
偏最小二乘法(PLS)和正交偏最小二乘法(OPLS)是统计模型,用于寻找两组数据矩阵之间的关系。它们广泛应用于化学计量学、生物信息学、经济预测等领域。 偏最小二乘法(PLS) 偏最小二乘法是一种多变量分析方法,主要用于找到两组数据(通常是预测变量集和响应变量集)之间…...

CDR2024最新版本怎么下载?Coreldraw相关快捷键教程分享
想必从事平面设计的大咖们都知道,Coreldraw是一款优秀的图形设计软件,被广泛地运用在平面设计、包装设计、服装设计各个生活领域,因此了解一些关于CorelDRAW快捷键的知识是很有必要的。因为使用快捷键不仅使用起来方便快捷,而且提…...

C语言实战项目<贪吃蛇>
我们这篇会使用C语言在Windows环境的控制台中模拟实现经典小游戏贪吃蛇 实现基本的功能: 结果如下: 1.一些Win32 API知识 本次实现呢我们会用到一些Win32 API的知识(WIN32 API也就是Microsoft Windows 32位平台的应用程序编程接口): 1)控制窗口大小 我们可以使用…...

人工智能时代:AI提示工程的奥秘 —— 驾驭大语言模型的秘密武器
文章目录 一、引言二、提示工程与大语言模型三、大语言模型的应用实践四、策略与技巧五、结语《AI提示工程实战:从零开始利用提示工程学习应用大语言模型》亮点内容简介作者简介目录获取方式 一、引言 随着人工智能技术的飞速发展,大语言模型作为一种新…...
Idea编写mapper.xml文件提示表名和字段
一、连接database 二、setting- > language -> sql Dialects中 的选项设为 mysql就可以了 三、测试...

解密人工智能:探索机器学习奥秘
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. 机器学习的定义二. 机器学习的发展历程三. 机器学习的原理四. 机器学习的分类…...
C语言第十四弹---函数递归
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 函数递归 1、递归是什么? 1.1、递归的思想 1.2、递归的限制条件 2、递归举例 2.1、举例1:求n的阶乘 2.1.1、分析和代码实现 2.1.2、…...
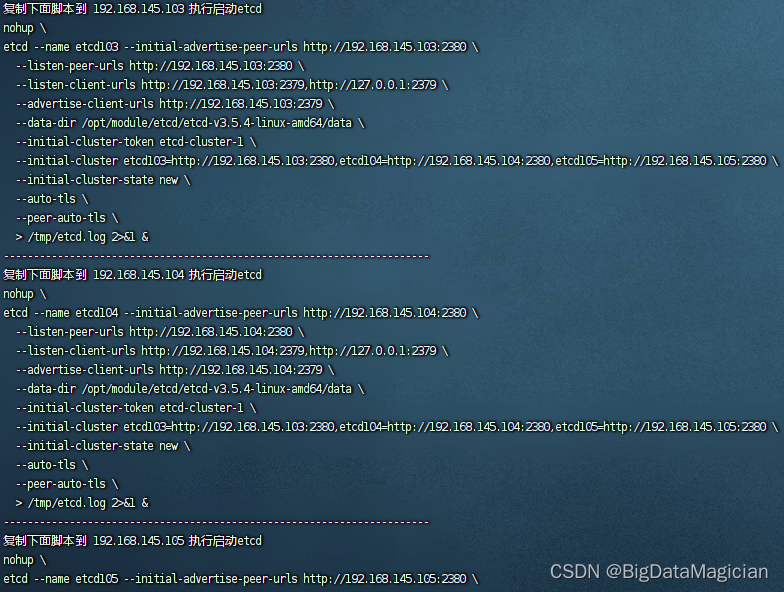
etcd自动化安装配置教程
文章目录 前言一、简介1. 简介2. 特点3. 端口介绍 二、etcd安装教程(单机版)1. 复制脚本2. 增加执行权限3. 执行脚本4. 查看启动状态5. 卸载etcd 三、etcd安装教程(集群版)1. 复制脚本2. 增加执行权限3. 分发脚本4. 执行脚本5. 启…...
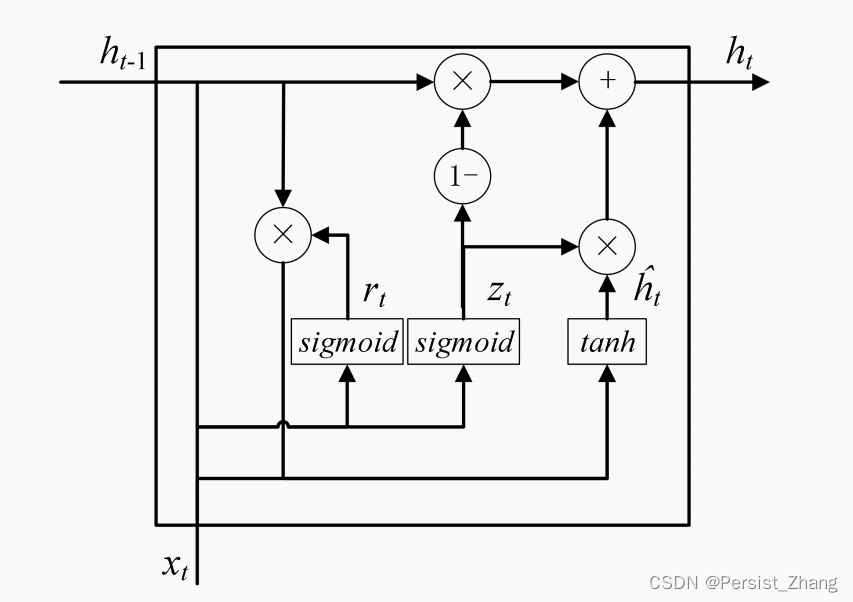
时间序列预测——GRU模型
时间序列预测——GRU模型 在深度学习领域,循环神经网络(RNN)是处理时间序列数据的一种常见选择。上期已介绍了LSTM的单步和多步预测。本文将深入介绍一种LSTM变体——门控循环单元(GRU)模型,包括其理论基础…...
通用CI/CD软件平台TeamCity全新发布v2023.11——增强Git托管平台的集成
TeamCity是一个通用的 CI/CD 软件平台,可以实现灵活的工作流、协作和开发做法。我们的解决方案将帮助在您的 DevOps 流程中成功实现持续集成、持续交付和持续部署。 TeamCity 2023.11正式版下载 TeamCity 2023.11 带来了矩阵构建和构建缓存等多项备受期待的功能&a…...

C语言:register类型变量
register—— 寄存器存储 register 是 C 语言中的一种存储类别(Storage Class),它用于告诉编译器将变量存储在寄存器中。在 C 语言中,变量的存储位置可以是寄存器、堆栈或静态存储区,使用 register 存储类别可以帮助我…...
android 自定义下拉框
一、 简介: 原生Android 提供的spinner下拉框不怎么方便,样式有点丑。修改起来麻烦,于是就自己动手写了一下拉列表。 实现原理使用的是,popwindow弹框,可实现宽高自定义,下拉列表使用listview. 二、pop弹框…...
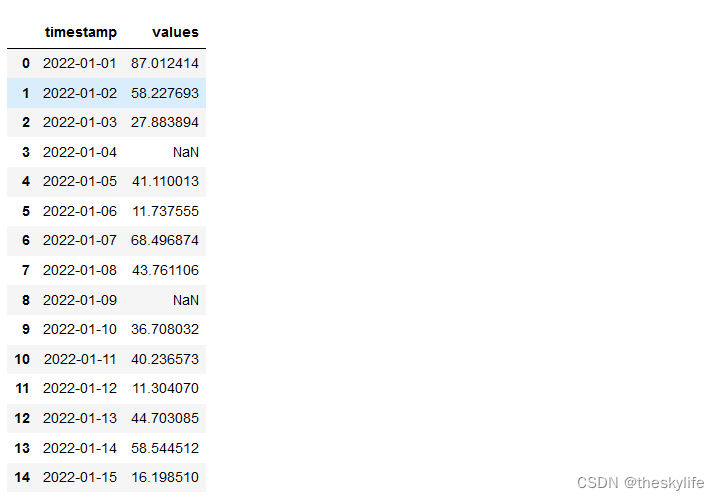
揭开时间序列的神秘面纱:特征工程的力量
目录 写在开头1. 什么是特征工程?1.1 特征工程的定义和基本概念1.2 特征工程在传统机器学习中的应用1.3 时间序列领域中特征工程的独特挑战和需求3. 时间序列数据的特征工程技术2.1 数据清洗和预处理2.1.1 缺失值处理2.1.2 异常值检测与处理2.2 时间特征的提取2.2.1 时间戳解析…...

vue3 源码解析(5)— patch 函数源码的实现
什么是 patch 在 vue 中 patch 函数的作用是在渲染的过程中,比较新旧节点的变化,通过打补丁的形式,进行新增、删除、移动或替换操作,此过程避免了大量的 dom 操作,提升了运行的性能。 patch 执行流程 patch 函数整体…...
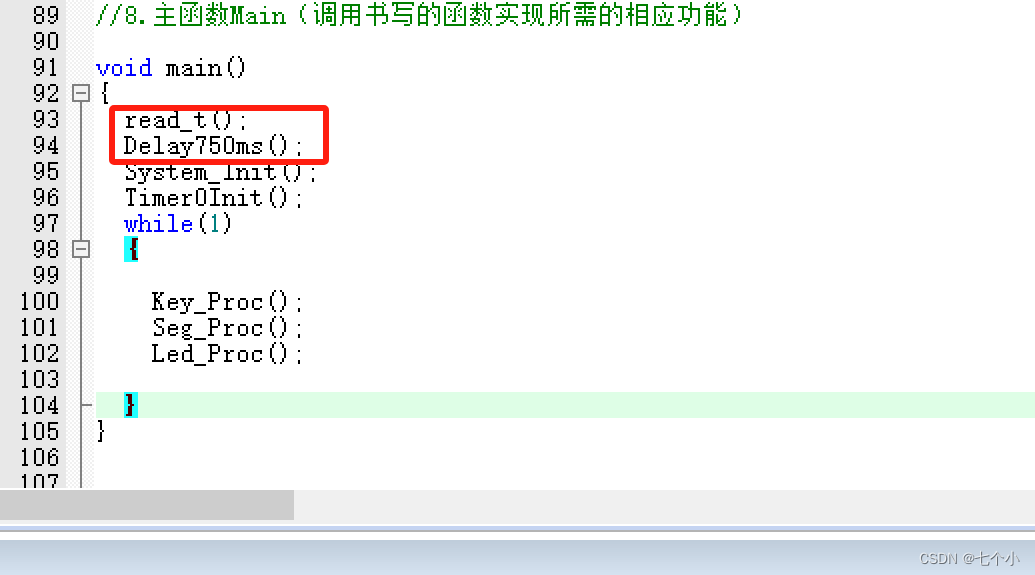
蓝桥杯2024/1/28----十二届省赛题笔记
题目要求: 2、 竞赛板配置要求 2.1将 IAP15F2K61S2 单片机内部振荡器频率设定为 12MHz。 2.2键盘工作模式跳线 J5 配置为 KBD 键盘模式。 2.3扩展方式跳线 J13 配置为 IO 模式。 2.4 请注意 : 选手需严格按照以上要求配置竞赛板,编写和调…...
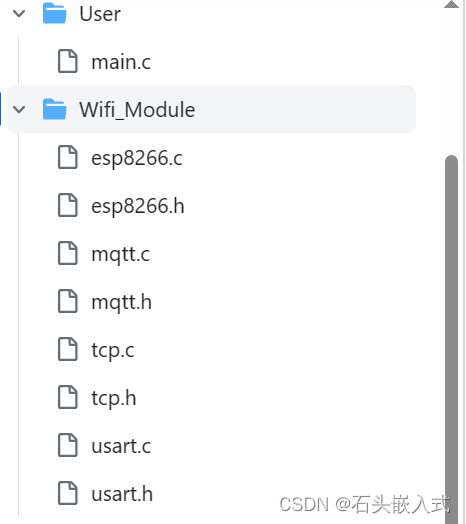
STM32+ESP8266 实现物联网设备节点
目录 一、硬件准备 二、编译环境 三、源代码地址 四、说明 五、测试方法 六、所有测试工具和文档 本项目使用stm32F103ZEesp8266实现一个物联网的通信节点,目前支持的协议有mqtt,tcp。后续会持续更新,增加JSON,传感器&#…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
