【Leetcode】2670. 找出不同元素数目差数组
文章目录
- 题目
- 思路
- 代码
- 结果
题目
题目链接
给你一个下标从 0 开始的数组 nums ,数组长度为 n 。
nums 的 不同元素数目差 数组可以用一个长度为 n 的数组 diff 表示,其中 diff[i] 等于前缀 nums[0, …, i] 中不同元素的数目 减去 后缀 nums[i + 1, …, n - 1] 中不同元素的数目。
返回 nums 的 不同元素数目差 数组。
注意 nums[i, …, j] 表示 nums 的一个从下标 i 开始到下标 j 结束的子数组(包含下标 i 和 j 对应元素)。特别需要说明的是,如果 i > j ,则 nums[i, …, j] 表示一个空子数组。
示例1:
输入:nums = [1,2,3,4,5]
输出:[-3,-1,1,3,5]
解释:
对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 4 个不同的元素。因此,diff[0] = 1 - 4 = -3 。
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
对于 i = 2,前缀中有 3 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 3 - 2 = 1 。
对于 i = 3,前缀中有 4 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 4 - 1 = 3 。
对于 i = 4,前缀中有 5 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 5 - 0 = 5 。
示例2:
输入:nums = [3,2,3,4,2]
输出:[-2,-1,0,2,3]
解释:
对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[0] = 1 - 3 = -2 。
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
对于 i = 2,前缀中有 2 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 2 - 2 = 0 。
对于 i = 3,前缀中有 3 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 3 - 1 = 2 。
对于 i = 4,前缀中有 3 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 3 - 0 = 3 。
提示:
- 1 <= n == nums.length <= 50
- 1 <= nums[i] <= 50
思路
这道题是一个简单的模拟题,需要维护不同的元素,那就可以直接想到使用set或者unordered_set,这里直接用unordered_set,遍历所有可能的前缀大小。然后,使用嵌套循环将前缀的元素添加到集合中,使用另一个嵌套循环将后缀的元素添加到另一个集合中。然后把两个集合中的元素作差存储。
代码
class Solution {
public:vector<int> distinctDifferenceArray(vector<int>& nums) {int n = nums.size();vector<int> ans;for(int i = 0; i < n; i ++){unordered_set<int> s1, s2;for(int j = 0; j <= i; j ++) s1.insert(nums[j]);for(int k = i + 1; k < n; k ++) s2.insert(nums[k]);ans.push_back(s1.size() - s2.size());}return ans;}
};
结果

相关文章:

【Leetcode】2670. 找出不同元素数目差数组
文章目录 题目思路代码结果 题目 题目链接 给你一个下标从 0 开始的数组 nums ,数组长度为 n 。 nums 的 不同元素数目差 数组可以用一个长度为 n 的数组 diff 表示,其中 diff[i] 等于前缀 nums[0, …, i] 中不同元素的数目 减去 后缀 nums[i 1, …, …...
༺༽༾ཊ—Unity之-01-工厂方法模式—ཏ༿༼༻
首先创建一个项目, 在这个初始界面我们需要做一些准备工作, 建基础通用文件夹, 创建一个Plane 重置后 缩放100倍 加一个颜色, 任务:使用工厂方法模式 创建 飞船模型, 首先资源商店下载飞船模型,…...

QT仪表盘小工具
头文件: /**************************************************************************** ** ** Copyright (C) 2016 The Qt Company Ltd. ** Contact: https://www.qt.io/licensing/ ** ** This file is part of the examples of the Qt Toolkit. ** ** $QT_BEGIN_LICENSE…...

【2024】大三寒假再回首:缺乏自我意识是毒药,反思和回顾是解药
2024年初,学习状态回顾 开稿时间:2024-1-23 归家百里去,飘雪送客迟。 搁笔日又久,一顾迷惘时。 我们饱含着过去的习惯,缺乏自我意识是毒药,反思和回顾是解药。 文章目录 2024年初,学习状态回顾一…...

计算机网络——网络层(3)
计算机网络——网络层(3) 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU)1 网络层——控制平面因特网中自治系统内部的路由选择总括考虑因素总结 ISP之间的路由选择:BGP考虑因素总结 SDN控制层面重要组件和功能总结 ICMP主要功能和特点…...

ROS2 学习笔记12:使用 colcon 构建软件包
ROS2 学习笔记12:使用 colcon 构建软件包 Background 背景Prerequisites 前提1 Install colcon2 Install ROS 2 Basics 基础1 Create a workspace2 Add some sources3 Source an underlay4 Build the workspace5 Run tests6 Source the environment7 Try a demo Cre…...
基于JAVA+SpringBoot+Vue的前后端分离的医院管理系统
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 随着计算机科学的迅猛…...

npm淘宝镜像过期解决办法
npm淘宝镜像过期解决办法 因为npm 官方镜像(registry.npmjs.org)在国内访问很慢,我们基本上都会选择切换到国内的一些 npm 镜像(淘宝镜像、腾讯云镜像等)。由于淘宝原来的镜像(registry.npm.taobao.org&am…...

Arduino 官网上下载和使用开发板
在 Arduino 官网上下载和使用开发板可以按照以下步骤进行: 打开浏览器,访问 Arduino 官网(https://www.arduino.cc/)。在官网首页,可以看到各种型号的 Arduino 开发板和相关产品。根据自己的需求选 择合适的开发板型号…...

k8s学习-DaemonSet和Job
1.1DaemonSet是什么 Deployment部署的副本Pod会分布在各个Node上,每个Node都可能运行好几个副本。DaemonSet的不同之处在于:每个Node上最多只能运行⼀个副本。DaemonSet的典型应用场景有: (1)在集群的每个节点上运⾏存…...

【开源】SpringBoot框架开发海南旅游景点推荐系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用户端2.2 管理员端 三、系统展示四、核心代码4.1 随机景点推荐4.2 景点评价4.3 协同推荐算法4.4 网站登录4.5 查询景点美食 五、免责说明 一、摘要 1.1 项目介绍 基于VueSpringBootMySQL的海南旅游推荐系统ÿ…...
Windows10更新失败 错误 0x80070643、KB5034441的解决方法之二
Windows10更新失败 错误 0x80070643、KB5034441 在知乎Windows10更新失败 错误 0x80070643、KB5034441的原因分析和几个解决方法 - 知乎 参考文章进行操作,更详细信息自己看上面链接。 我电脑的硬盘是mbr格式,而且没有划分恢复分区。 Microsoft Windo…...

SQL中LIMIT的简单用法
在SQL的世界里,有一位神秘而强大的限制者,它就是 LIMIT。今天,我们将深入探讨这个神秘的SQL关键字,揭开它的神秘面纱,让你能够更好地使用它来操控你的数据。 背景 首先,让我们了解一下为什么我们需要 LIM…...

canvas自定义扩展方法:文字自动换行
查看专栏目录 canvas实例应用100专栏,提供canvas的基础知识,高级动画,相关应用扩展等信息。canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重…...
【2024全网最详细】Google 搜索命令终极指南
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 你是否尝试过使用 Google 搜索作为免费的 SEO …...
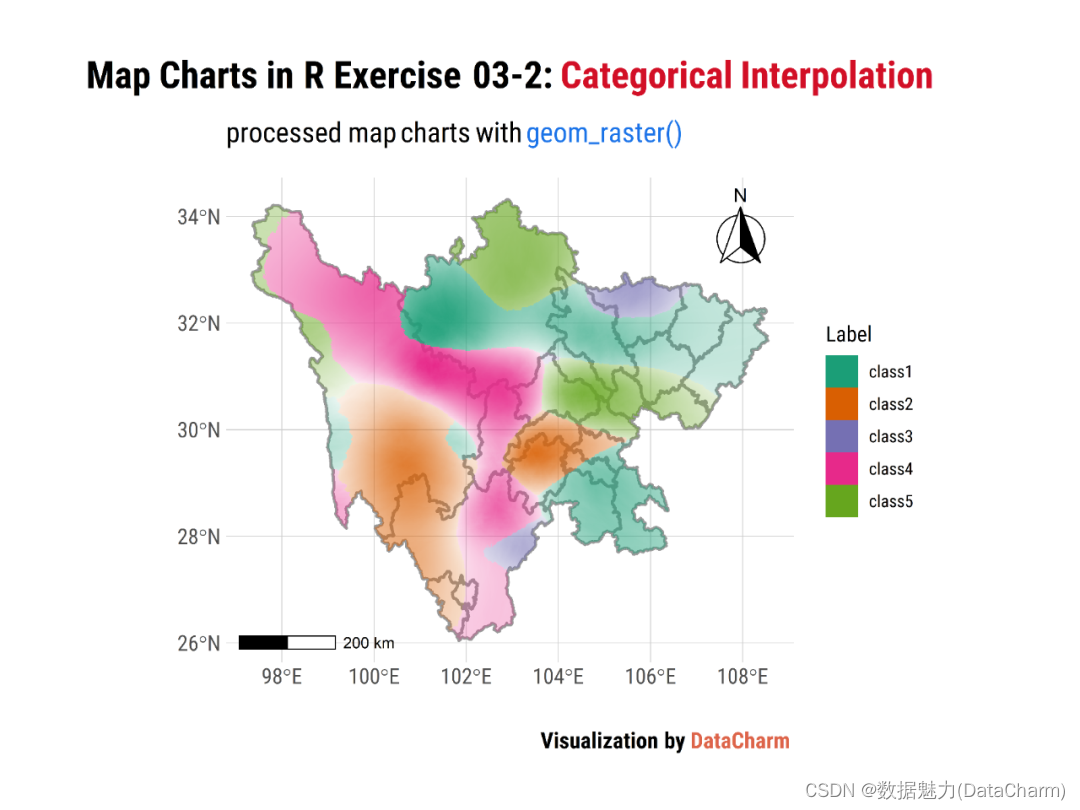
R-kknn包-类别插值可视化绘制
前面的推文我们介绍了使用scikit-learn结合分类散点数据,构建机器学习分类模型并将模型结果可视化展示,具体链接如下: 机器学习和可视化还能一起这样用?Python教你全搞定。今天这篇推文,我们就使用R语言的kknn包进行类…...
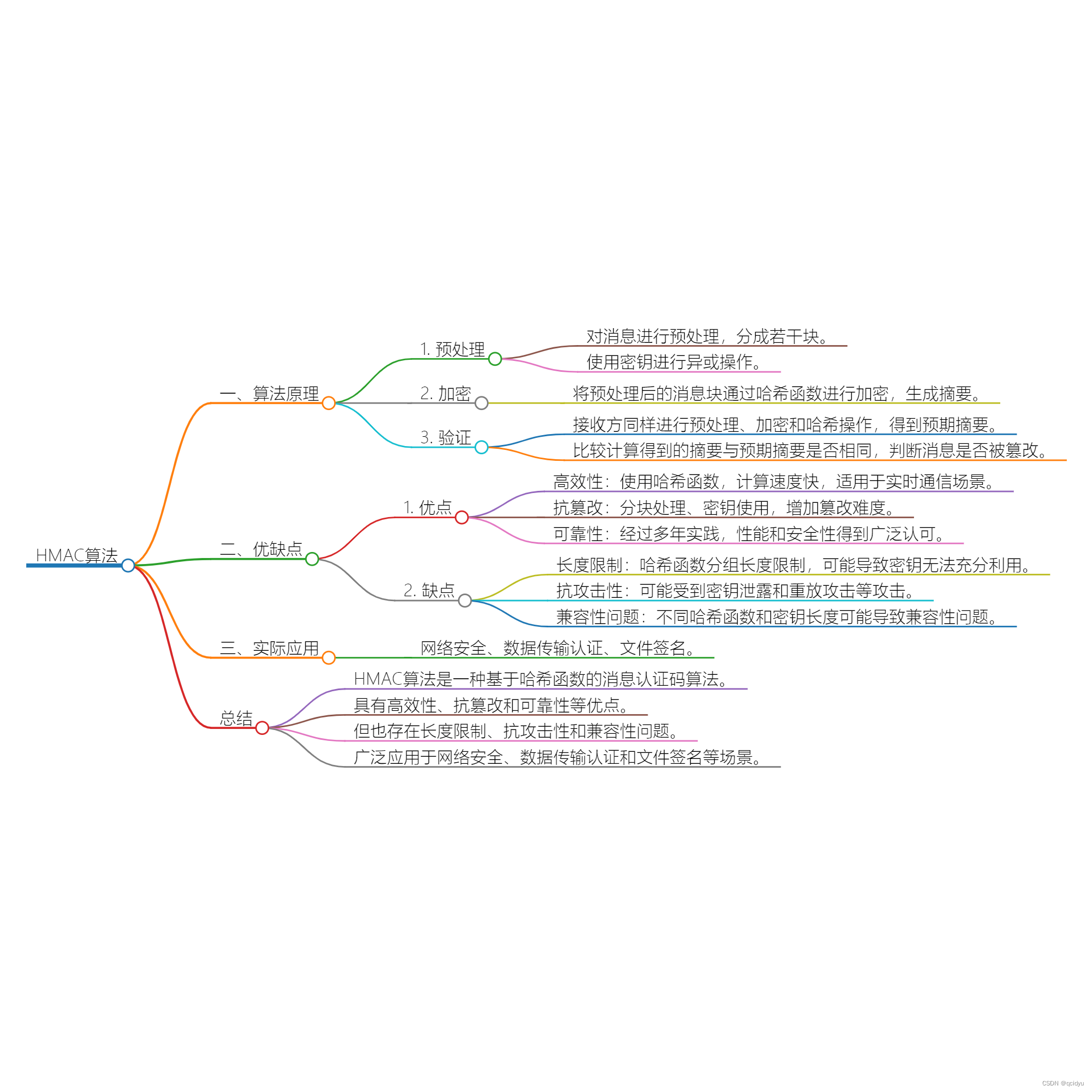
探究HMAC算法:消息认证与数据完整性的完美结合
Hash-based Message Authentication Code(基于哈希的消息认证码,简称HMAC)算法作为一种广泛应用的消息认证码(MAC)算法,在现代信息安全领域起着至关重要的作用。本文将从算法原理、优缺点、实际应用等方面&…...

10s 内得到一个干净、开箱即用的 Linux 系统
安装 使用官方脚本安装我的服务器不行 官方脚本 mkdir instantbox && cd $_ bash <(curl -sSL https://raw.githubusercontent.com/instantbox/instantbox/master/init.sh) 下面是我的完整安装过程 mkdir /opt/instantbox cd /opt/instantbox 1.脚本文件 (这个没…...
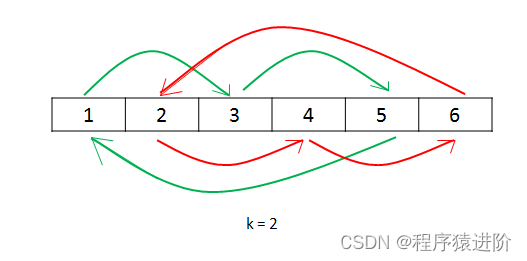
轮转数组[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个整数数组nums,将数组中的元素向右轮转k个位置,其中k是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,…...
【SpringBoot系列】自动装配的魅力:Spring Boot vs 传统Spring
IT行业有哪些证书含金量高? 文章目录 IT行业有哪些证书含金量高?强烈推荐前言区别项目配置:依赖管理:内嵌服务器:开发体验: 实例Spring项目示例:Spring Boot项目示例: 总结强烈推荐专栏集锦写在最后 强烈…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
