坚持刷题 | 完全二叉树的节点个数
Hello,大家好,我是阿月!坚持刷题,老年痴呆追不上我,今天刷:完全二叉树的节点个数
题目
222.完全二叉树的节点个数
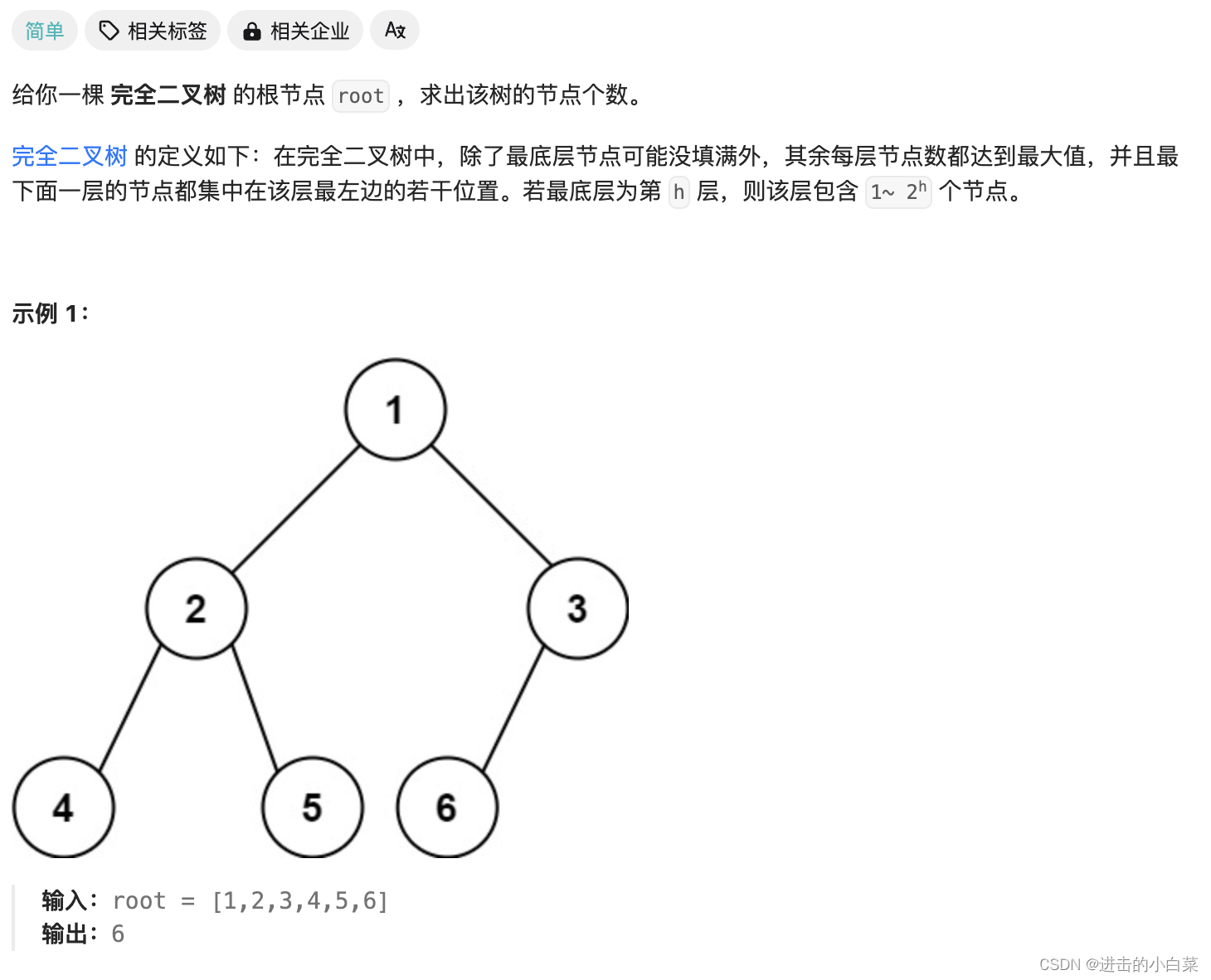
代码实现
class TreeNode {int val;TreeNode left, right;public TreeNode(int val) {this.val = val;this.left = this.right = null;}
}public class CompleteBinaryTreeCount {// 计算完全二叉树的节点个数public int countNodes(TreeNode root) {if (root == null) {return 0;}int leftHeight = leftHeight(root);int rightHeight = rightHeight(root);if (leftHeight == rightHeight) {// 左子树是满二叉树return (1 << leftHeight) - 1;} else {// 左子树不是满二叉树,递归计算左右子树的节点数return 1 + countNodes(root.left) + countNodes(root.right);}}// 计算左子树的高度private int leftHeight(TreeNode root) {int height = 0;while (root != null) {height++;root = root.left;}return height;}// 计算右子树的高度private int rightHeight(TreeNode root) {int height = 0;while (root != null) {height++;root = root.right;}return height;}public static void main(String[] args) {// 创建一个完全二叉树示例TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);root.right.left = new TreeNode(6);CompleteBinaryTreeCount solution = new CompleteBinaryTreeCount();int nodeCount = solution.countNodes(root);System.out.println("完全二叉树的节点个数: " + nodeCount);}
}
实现总结
- 完全二叉树:完全二叉树的定义是除了最后一层外,其它各层的节点数都达到最大值,且最后一层的节点依次从左到右排列。这一特性对计算节点数有重要影响。
- 确定解题方法:常见的方法包括递归和迭代。在了解完全二叉树的性质后,可以选择合适的方法求解节点数,上面实现就采用了递归的方式实现。
- 确定节点数计算方式:针对完全二叉树的特性,可以通过一些方法,如树的高度、子树的特性等来计算节点数。上面实现通过计算左子树和右子树的高度来确定完全二叉树的结构,如果左右子树高度相等,则左子树是满二叉树,节点个数可以通过2的幂次方计算。如果左右子树高度不等,则递归计算左右子树的节点数。
- 考虑边界情况:对于空树或者只有根节点的情况,需要特殊处理。
- 时间复杂度:
O(log^2 N)。递归的深度为树的高度,每次递归中需要计算左右子树的高度,因此时间复杂度为O(log N),其中 N 为节点个数。在每层递归中,都需要进行一次高度计算,高度计算的时间复杂度也为O(log N),因此总体时间复杂度为O(log^2 N)。
相关文章:

坚持刷题 | 完全二叉树的节点个数
Hello,大家好,我是阿月!坚持刷题,老年痴呆追不上我,今天刷:完全二叉树的节点个数 题目 222.完全二叉树的节点个数 代码实现 class TreeNode {int val;TreeNode left, right;public TreeNode(int val) …...

K8S网络
一、介绍 k8s不提供网络通信,提供了CNI接口(Container Network Interface,容器网络接口),由CNI插件实现完成。 1.1 Pod通信 1.1.1 同一节点Pod通信 Pod通过虚拟Ethernet接口对(Veth Pair)与外部通信,Veth…...

【蓝桥杯51单片机入门记录】LED
目录 一、基础 (1)新建工程 (2)编写前准备 二、LED (1)点亮LED灯 (2)LED闪烁 延时函数的生成(stc-isp中生成) 实现 (3)流水灯…...
)
轻松使用python将PDF转换为图片(成功)
使用PyMuPDF(fitz)将PDF转换为图片 在处理PDF文件时,我们经常需要将PDF页面转换为图片格式,以便于在网页、文档或应用程序中显示。Python提供了多种方式来实现这一需求,本文将介绍如何使用PyMuPDF(也称为f…...

【目标检测】对DETR的简单理解
【目标检测】对DETR的简单理解 文章目录 【目标检测】对DETR的简单理解1. Abs2. Intro3. Method3.1 模型结构3.2 Loss 4. Exp5. Discussion5.1 二分匹配5.2 注意力机制5.3 方法存在的问题 6. Conclusion参考 1. Abs 两句话概括: 第一个真正意义上的端到端检测器最…...

[工具探索]Safari 和 Google Chrome 浏览器内核差异
最近有些Vue3的项目,使用了safari进行测试环境搞开发,发现页面存在不同程序的页面乱码情况,反而google浏览器没问题,下面我们就对比下他们之间的差异点: 日常开发google chrome占多数;现在主流浏览器 Goog…...

文本生成高清、连贯视频,谷歌推出时空扩散模型
谷歌研究人员推出了创新性文本生成视频模型——Lumiere。 与传统模型不同的是,Lumiere采用了一种时空扩散(Space-time)U-Net架构,可以在单次推理中生成整个视频的所有时间段,能明显增强生成视频的动作连贯性ÿ…...

时隔3年 | 微软 | Windows Server 2025 重磅发布
最新功能 以下是微软产品团队正在努力的方向: Windows Server 2025 为所有人提供的热补丁下一代 AD 活动目录和 SMB数据与存储Hyper-V 和人工智能还有更多… Ignite 发布视频 Windows Server 2025 Ignite Video 介绍 Windows Server 2022 正式发布日期是2021年…...

有趣的css - 动态的毛玻璃背景
页面效果 此效果主要使用 backdrop-filter 属性,以及配合 animation 属性来实现毛玻璃模糊和一些动效。 此效果可适用于登录窗口,网站背景或者一些卡片列表中,使网页更具科技感和空间感。 核心代码部分,简要说明了写法思路&#x…...

桥接模式解析
回调设计模式 意图 回调是指一段可以执行的代码,该代码会被作为参数传递给其他代码,在适当的时候,预期这部分代码将会被调用执行。 解释 案例:我们需要在执行完任务后得到通知。为此,我们会向执行器传递一个回调方法…...
MySQL数据库基础第一篇(SQL通用语法与分类)
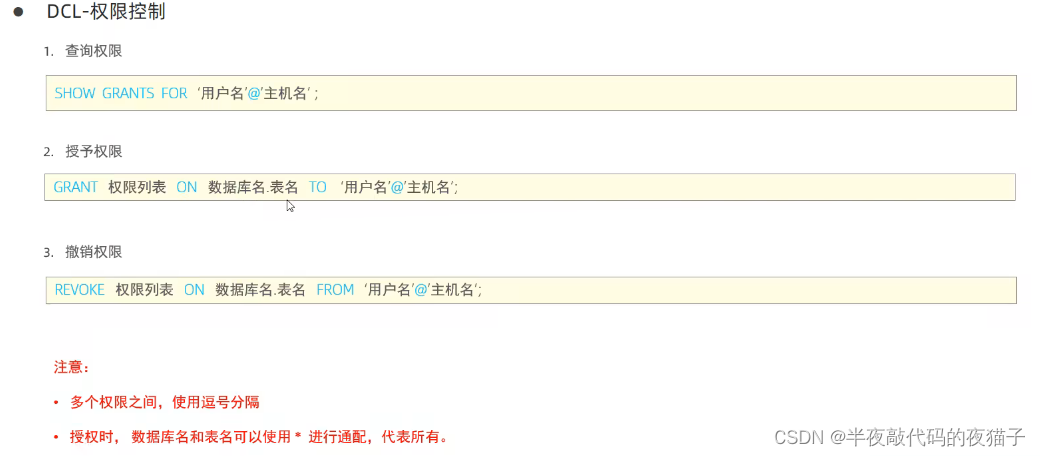
文章目录 一、SQL通用语法二、SQL分类三、DDL语句四、DML语句1.案例代码2.读出结果 五、DQL语句1.DQL-基本查询2.DQL-条件查询3.DQL-聚合函数4.DQL-分组查询5.DQL-排序查询6.DQL-分页查询7.DQL语句-执行顺序1.案例代码2.读出结果 六、DCL语句1.DCL-管理用户2.DCL-权限控制1.案例…...
【Qt学习笔记】(一)初识Qt
Qt学习笔记 1 使用Qt Creator 新建项目2 项目代码解释3 创建第一个 Hello World 程序4 关于内存泄漏问题5 Qt 中的对象树6 关于 qDebug()的使用7 使用其他方式创建一个 Hello World 程序(编辑框和按钮方式)8 关于 Qt 中的命名规范…...
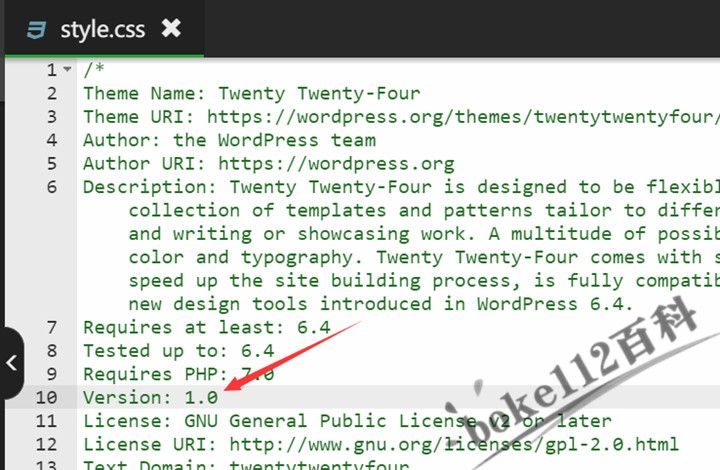
YIA主题如何关闭新版本升级提示?WordPress主题怎么取消升级提醒?
前两天YIA主题发布了升级到2.8版本,新增了一些功能,优化调整修复了一些功能,但是这些功能调整幅度不大,加上boke112百科使用的YIA主题已经进行了很多方面的个性化修改,所以就懒得升级了,但是每次进入WordPr…...
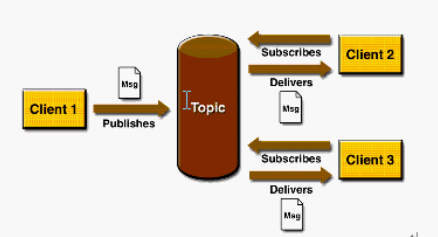
消息队列的应用场景
消息队列的应用场景 消息队列中间件是分布式系统中重要的组件,主要解决应用耦合,异步消息,流量削锋等问题实现高性能,高可用,可伸缩和最终一致性架构使用较多的消息队列有ActiveMQ,RabbitMQ,Ze…...
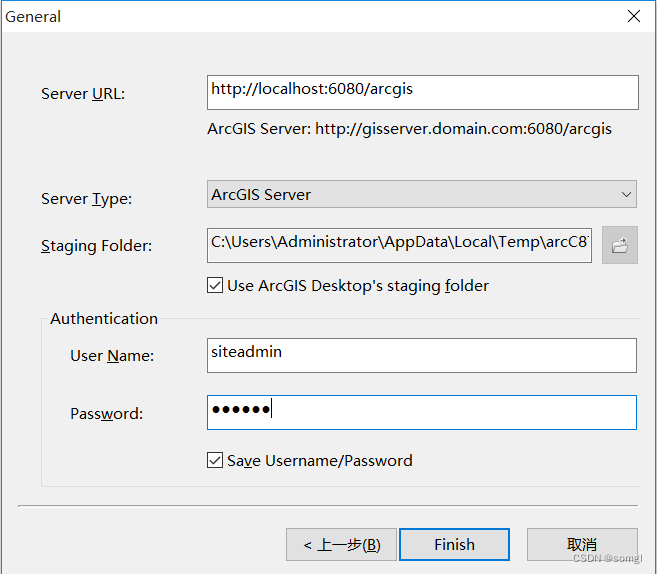
Arcgis10.3安装
所需软件地址 链接:https://pan.baidu.com/s/1aAykUDjkaXjdwFjDvAR83Q?pwdbs2i 提取码:bs2i 1、安装License Manager 点击License Manager.exe,默认下一步。 安装完,点击License Server Administrator,停止服务。…...
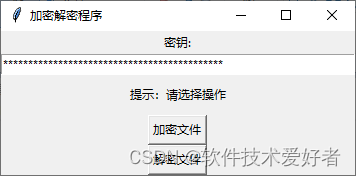
用Python和 Cryptography库给你的文件加密解密
用Python和 Cryptography库给你的文件加密解密 用Python和 Cryptography库给你的文件加把安全锁。 先介绍与加密解密有关的几个基本概念。 加密(Encryption):加密是将明文转换为密文的过程,使得未经授权的人无法读懂。 解密&a…...
element-ui button 仿写 demo
基于上篇 button 源码分享写了一个简单 demo,在写 demo 的过程中,又发现了一个小细节,分享一下: 1、组件部分: <template><buttonclass"yss-button"click"handleClick":class"[ty…...
Maya------创建多边形工具
配合导入图像使用 Tab键可以删除一个点! 模型不能超过4边面!多切割工具进行连接! 15.maya常用命令5.创建多边形工具 反转 双显 挤出_哔哩哔哩_bilibili...
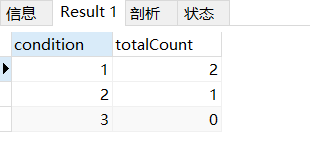
SQL分组统计条数时,不存在组类型,如何显示条数为0
首先有张表 CREATE TABLE person (id int NOT NULL AUTO_INCREMENT,name varchar(255) DEFAULT NULL,type int DEFAULT NULL,PRIMARY KEY (id) ) ENGINEInnoDB AUTO_INCREMENT2 DEFAULT CHARSETutf8mb4 COLLATEutf8mb4_0900_ai_ci;表里很简单三条数据: INSERT INT…...
)
通过日期计算星期函数(C语言版)
测试源代码: #include <stdio.h>int getDayOfWeek(int year, int month, int day) {if (month < 3) {month 12;year--;}int q day;int m month;int K year % 100;int J year / 100;int dayOfWeek (q 13 * (m 1) / 5 K K / 4 J / 4 - 2 * J) % …...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

SOC-ESP32S3部分:30-I2S音频-麦克风扬声器驱动
飞书文档https://x509p6c8to.feishu.cn/wiki/SKZzwIRH3i7lsckUOlzcuJsdnVf I2S简介 I2S(Inter-Integrated Circuit Sound)是一种用于传输数字音频数据的通信协议,广泛应用于音频设备中。 ESP32-S3 包含 2 个 I2S 外设,通过配置…...

[C++错误经验]case语句跳过变量初始化
标题:[C错误经验]case语句跳过变量初始化 水墨不写bug 文章目录 一、错误信息复现二、错误分析三、解决方法 一、错误信息复现 write.cc:80:14: error: jump to case label80 | case 2:| ^ write.cc:76:20: note: crosses initialization…...

Angular中Webpack与ngx-build-plus 浅学
Webpack 在 Angular 中的概念 Webpack 是一个模块打包工具,用于将多个模块和资源打包成一个或多个文件。在 Angular 项目中,Webpack 负责将 TypeScript、HTML、CSS 等文件打包成浏览器可以理解的 JavaScript 文件。Angular CLI 默认使用 Webpack 进行项目…...

Flask+LayUI开发手记(八):通用封面缩略图上传实现
前一节做了头像上传的程序,应该说,这个程序编写和操作都相当繁琐,实际上,头像这种缩略图在很多功能中都会用到,屏幕界面有限,绝不会给那么大空间摆开那么大一个界面,更可能的处理,就…...
