代码随想录算法训练营第三十三天|509. 斐波那契数 ,● 70. 爬楼梯 , 746. 使用最小花费爬楼梯
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
代码随想录
视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩_bilibili
509. 斐波那契数
代码随想录
视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili
class Solution {public int fib(int n) {if (n <= 1) {return n;}int arr[] = new int[n + 1];arr[0] = 0;arr[1] = 1;for (int i = 2; i <= n; i++) {arr[i] = arr[i - 1] + arr[i - 2];}return arr[n];}
}70. 爬楼梯
代码随想录
视频:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目_哔哩哔哩_bilibili
class Solution {public int climbStairs(int n) {//1.确定dp数组(dp table)以及下标的含义: dp[i]达到i阶有dp[i]种方法//2.确定递推公式:dp[i] = dp[i - 1] + dp[i - 2]//3.dp数组如何初始化: dp[0] = 1,(意义上说不通,代码跑的通) 所以,dp[1] = 1, dp[2] = 2//4.确定遍历顺序: 从前往后,因为后面要依赖前面的//5.举例推导dp数组: 查错int arr[] = new int[n];int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}746. 使用最小花费爬楼梯
代码随想录
视频讲解:动态规划开更了!| LeetCode:746. 使用最小花费爬楼梯_哔哩哔哩_bilibili
class Solution {public int minCostClimbingStairs(int[] cost) {//(站上面不花钱,开始跳才花钱)// 确定dp数组(dp table)以及下标的含义: 到达i的位置所需要的花费dp[i]// 确定递推公式: dp[i] = dp[i - 1] + cost[i - 1] / dp[i - 2] + cost[i - 2]// dp数组如何初始化: dp[1] dp[0]// 确定遍历顺序: 从前到后,后面的元素是依据前面的元素推导的// 举例推导dp数组int arr[] = new int[cost.length + 1];arr[0] = 0;arr[1] = 0;for (int i = 2; i < arr.length; i++) {arr[i] = Math.min(arr[i - 1] + cost[i - 1], arr[i - 2] + cost[i - 2]);}return arr[cost.length]; }
}解释cost.length + 1
- 数组长度为
cost.length:表示楼梯的每一步都有一个上升的成本。但是,这个数组不直接提供到达楼梯顶部(即最后一个台阶之后的位置)的成本。 - 额外的
+ 1位置:用于代表楼梯顶端的位置。这不是一个实际的台阶,而是一个达到所有台阶之后的终点位置。通过为这个终点位置分配一个状态,我们可以更简单地计算出达到这一点的最小成本。
相关文章:

代码随想录算法训练营第三十三天|509. 斐波那契数 ,● 70. 爬楼梯 , 746. 使用最小花费爬楼梯
确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 代码随想录 视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩…...

Node.js 文件系统操作指南
文章目录 Node.js 文件系统操作完全指南一、引言二、基本文件操作2.1 读取文件2.2 写入文件2.3 追加内容到文件 三、文件与目录的创建与删除3.1 创建文件3.2 创建目录3.3 删除文件3.4 删除目录 四、文件与目录的信息查询4.1 检查文件或目录是否存在4.2 获取文件信息4.3 获取目录…...

Kotlin 协程1:深入理解withContext
Kotlin 协程1:深入理解withContext 引言 在现代编程中,异步编程已经变得非常重要。在 Kotlin 中,协程提供了一种优雅和高效的方式来处理异步编程和并发。在这篇文章中,我们将深入探讨 Kotlin 协程中的一个重要函数:wi…...
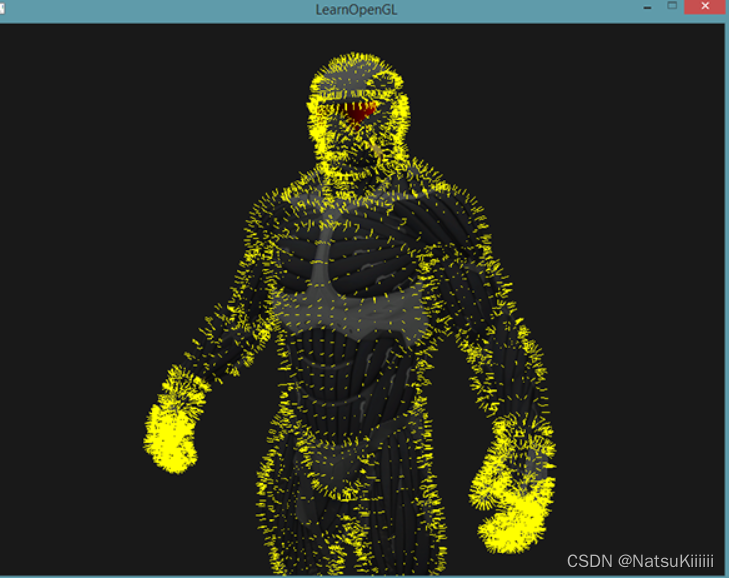
(自用)learnOpenGL学习总结-高级OpenGL-几何着色器
在顶点着色器和片段着色器中间还有一个几何着色器。 几何着色器的输入是一个图元的一组顶点,在几何着色器中进行任意变换之后再给片段着色器,可以变成完全不一样的图元、可以生成更多的顶点。 #version 330 core layout (points) in; layout (line_str…...
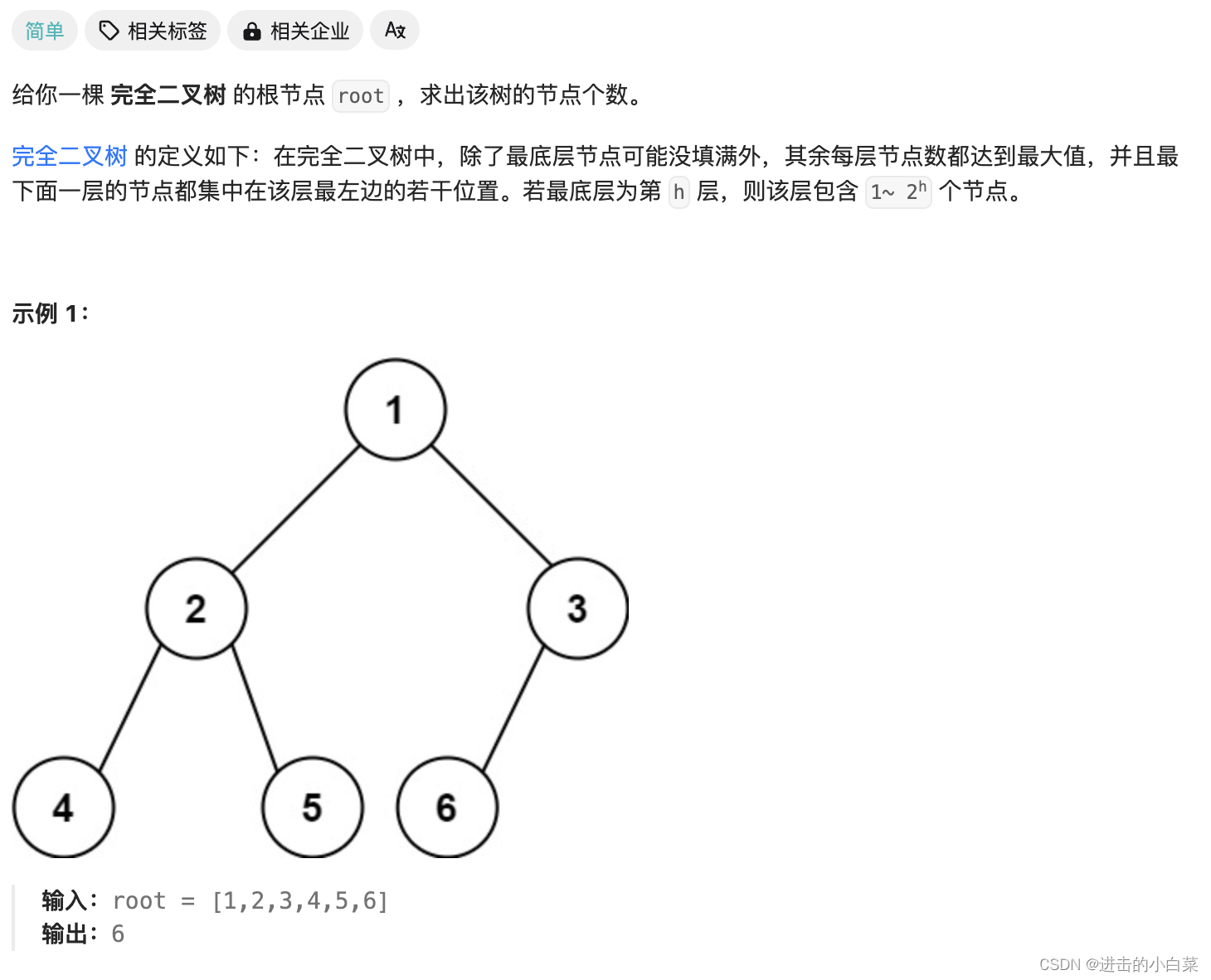
坚持刷题 | 完全二叉树的节点个数
Hello,大家好,我是阿月!坚持刷题,老年痴呆追不上我,今天刷:完全二叉树的节点个数 题目 222.完全二叉树的节点个数 代码实现 class TreeNode {int val;TreeNode left, right;public TreeNode(int val) …...

K8S网络
一、介绍 k8s不提供网络通信,提供了CNI接口(Container Network Interface,容器网络接口),由CNI插件实现完成。 1.1 Pod通信 1.1.1 同一节点Pod通信 Pod通过虚拟Ethernet接口对(Veth Pair)与外部通信,Veth…...

【蓝桥杯51单片机入门记录】LED
目录 一、基础 (1)新建工程 (2)编写前准备 二、LED (1)点亮LED灯 (2)LED闪烁 延时函数的生成(stc-isp中生成) 实现 (3)流水灯…...
)
轻松使用python将PDF转换为图片(成功)
使用PyMuPDF(fitz)将PDF转换为图片 在处理PDF文件时,我们经常需要将PDF页面转换为图片格式,以便于在网页、文档或应用程序中显示。Python提供了多种方式来实现这一需求,本文将介绍如何使用PyMuPDF(也称为f…...

【目标检测】对DETR的简单理解
【目标检测】对DETR的简单理解 文章目录 【目标检测】对DETR的简单理解1. Abs2. Intro3. Method3.1 模型结构3.2 Loss 4. Exp5. Discussion5.1 二分匹配5.2 注意力机制5.3 方法存在的问题 6. Conclusion参考 1. Abs 两句话概括: 第一个真正意义上的端到端检测器最…...

[工具探索]Safari 和 Google Chrome 浏览器内核差异
最近有些Vue3的项目,使用了safari进行测试环境搞开发,发现页面存在不同程序的页面乱码情况,反而google浏览器没问题,下面我们就对比下他们之间的差异点: 日常开发google chrome占多数;现在主流浏览器 Goog…...

文本生成高清、连贯视频,谷歌推出时空扩散模型
谷歌研究人员推出了创新性文本生成视频模型——Lumiere。 与传统模型不同的是,Lumiere采用了一种时空扩散(Space-time)U-Net架构,可以在单次推理中生成整个视频的所有时间段,能明显增强生成视频的动作连贯性ÿ…...

时隔3年 | 微软 | Windows Server 2025 重磅发布
最新功能 以下是微软产品团队正在努力的方向: Windows Server 2025 为所有人提供的热补丁下一代 AD 活动目录和 SMB数据与存储Hyper-V 和人工智能还有更多… Ignite 发布视频 Windows Server 2025 Ignite Video 介绍 Windows Server 2022 正式发布日期是2021年…...

有趣的css - 动态的毛玻璃背景
页面效果 此效果主要使用 backdrop-filter 属性,以及配合 animation 属性来实现毛玻璃模糊和一些动效。 此效果可适用于登录窗口,网站背景或者一些卡片列表中,使网页更具科技感和空间感。 核心代码部分,简要说明了写法思路&#x…...

桥接模式解析
回调设计模式 意图 回调是指一段可以执行的代码,该代码会被作为参数传递给其他代码,在适当的时候,预期这部分代码将会被调用执行。 解释 案例:我们需要在执行完任务后得到通知。为此,我们会向执行器传递一个回调方法…...
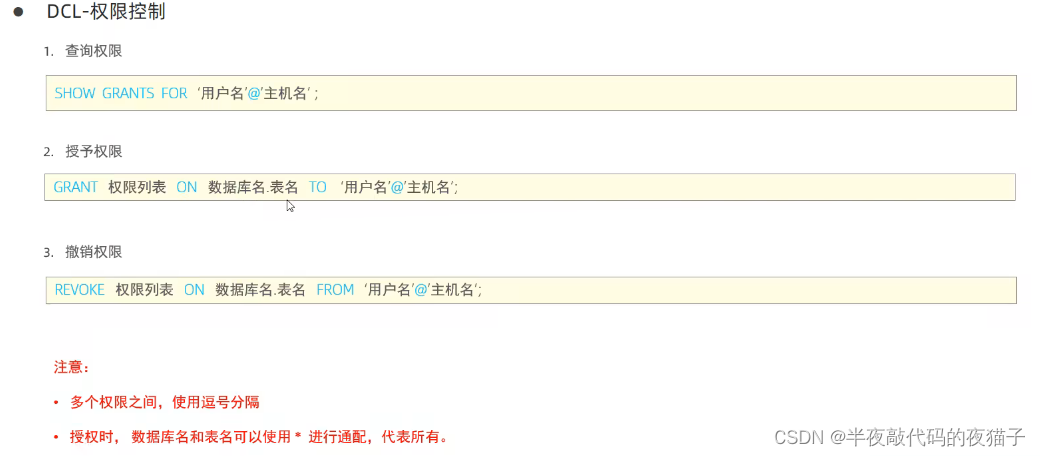
MySQL数据库基础第一篇(SQL通用语法与分类)
文章目录 一、SQL通用语法二、SQL分类三、DDL语句四、DML语句1.案例代码2.读出结果 五、DQL语句1.DQL-基本查询2.DQL-条件查询3.DQL-聚合函数4.DQL-分组查询5.DQL-排序查询6.DQL-分页查询7.DQL语句-执行顺序1.案例代码2.读出结果 六、DCL语句1.DCL-管理用户2.DCL-权限控制1.案例…...
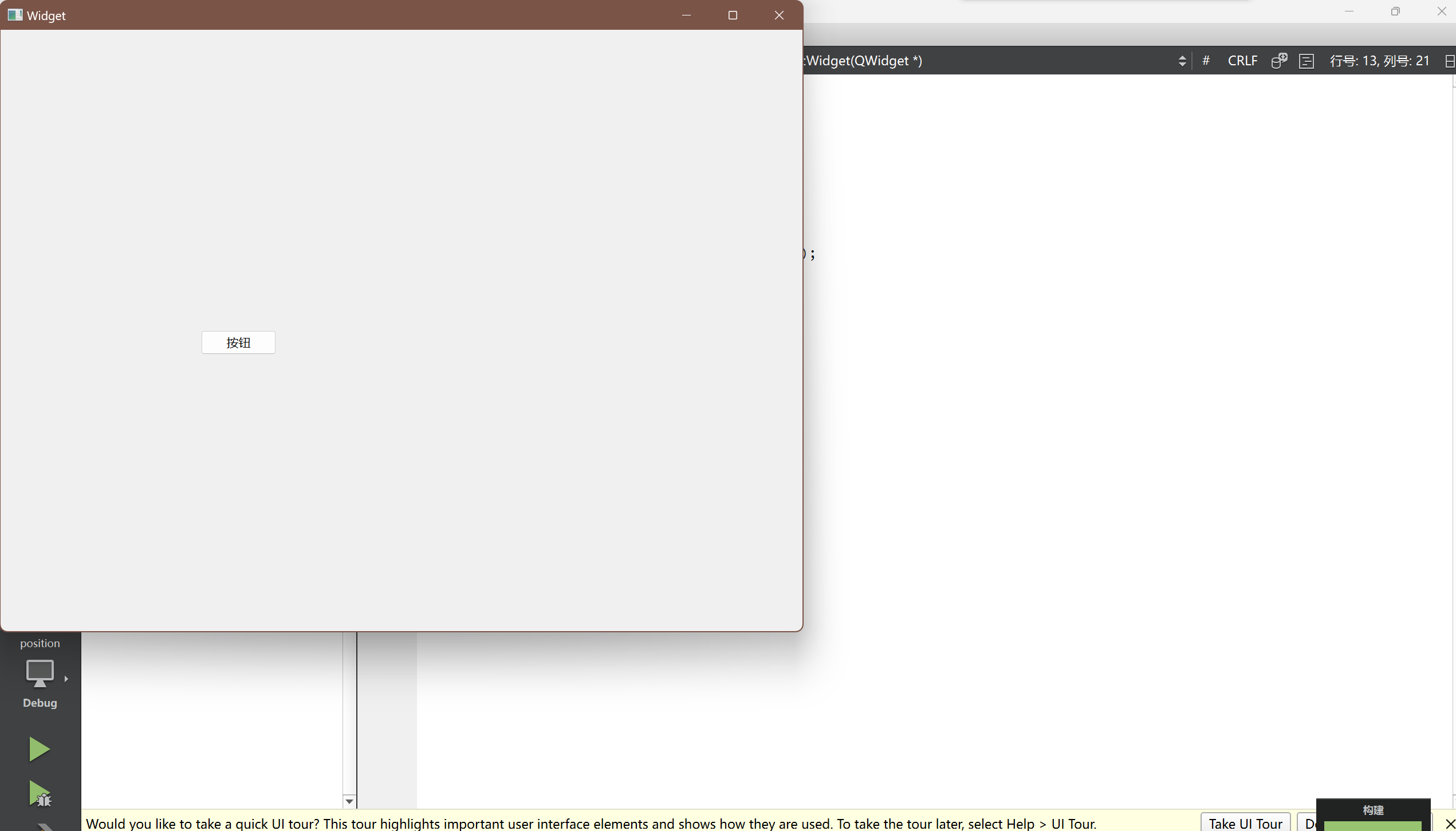
【Qt学习笔记】(一)初识Qt
Qt学习笔记 1 使用Qt Creator 新建项目2 项目代码解释3 创建第一个 Hello World 程序4 关于内存泄漏问题5 Qt 中的对象树6 关于 qDebug()的使用7 使用其他方式创建一个 Hello World 程序(编辑框和按钮方式)8 关于 Qt 中的命名规范…...
YIA主题如何关闭新版本升级提示?WordPress主题怎么取消升级提醒?
前两天YIA主题发布了升级到2.8版本,新增了一些功能,优化调整修复了一些功能,但是这些功能调整幅度不大,加上boke112百科使用的YIA主题已经进行了很多方面的个性化修改,所以就懒得升级了,但是每次进入WordPr…...
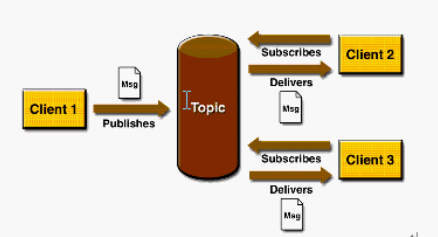
消息队列的应用场景
消息队列的应用场景 消息队列中间件是分布式系统中重要的组件,主要解决应用耦合,异步消息,流量削锋等问题实现高性能,高可用,可伸缩和最终一致性架构使用较多的消息队列有ActiveMQ,RabbitMQ,Ze…...
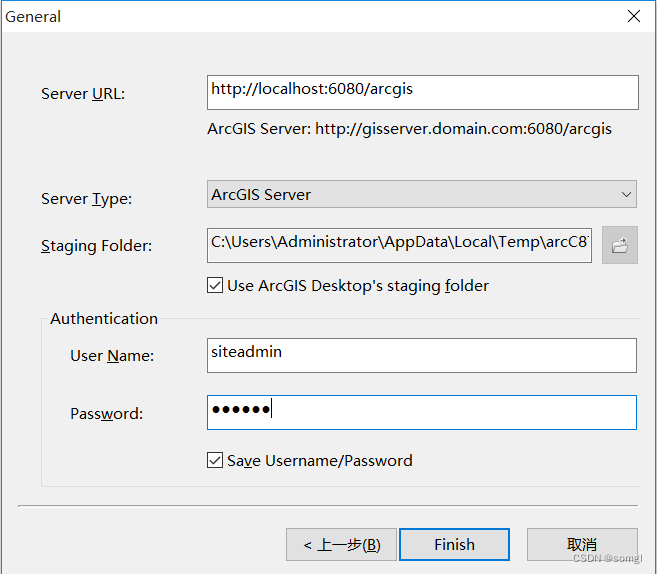
Arcgis10.3安装
所需软件地址 链接:https://pan.baidu.com/s/1aAykUDjkaXjdwFjDvAR83Q?pwdbs2i 提取码:bs2i 1、安装License Manager 点击License Manager.exe,默认下一步。 安装完,点击License Server Administrator,停止服务。…...
用Python和 Cryptography库给你的文件加密解密
用Python和 Cryptography库给你的文件加密解密 用Python和 Cryptography库给你的文件加把安全锁。 先介绍与加密解密有关的几个基本概念。 加密(Encryption):加密是将明文转换为密文的过程,使得未经授权的人无法读懂。 解密&a…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
