Java 数据结构篇-实现二叉搜索树的核心方法
🔥博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍


文章目录
1.0 二叉搜索树的概述
2.0 二叉搜索树的成员变量及其构造方法
3.0 实现二叉树的核心接口
3.1 实现二叉搜索树 - 获取值 get(int key)
3.2 实现二叉搜索树 - 获取最小的关键字 min(BinaryNode node)
3.3 实现二叉搜索树 - 获取最大的关键字 max(BinaryNode node)
3.4 实现二叉搜索树 - 增、更新 put( int key, Object value)
3.5 实现二叉搜索树 - 查找关键字的后驱节点 successor(int key)
3.6 实现二叉搜索树 - 查找关键字的前驱节点 predecessor(int key)
3.7 实现二叉搜索树 - 删除关键字节点 delete(int key)
3.8 实现二叉搜索树 - 查找范围小于关键字的节点值 less(int key)
3.9 实现二叉搜索树 - 查找范围大于关键字的节点值 greater(int key)
4.0 实现二叉搜索树 - 查找范围大于 k1 且小于 k2 关键字的节点值 between(int k1, int k2)
5.0 实现二叉搜索树核心方法的完整代码
1.0 二叉搜索树的概述
二叉搜索树是一种数据结构,用于存储数据并支持快速的插入、删除和搜索操作。它是一种树形结构。
它具有以下特点:
- 每个节点最多有两个子节点,分别称为左子节点和右子节点。
- 对于每个节点,其左子节点的值小于该节点的值,右子节点的值大于该节点的值。
- 中序遍历二叉搜索树可以得到有序的元素序列。
由于其特性,二叉搜索树在插入、删除和搜索操作上具有较高的效率。在平均情况下,这些操作的时间复杂度为 O(log n),其中 n 为树中节点的数量。然而,如果树的结构不平衡,最坏情况下这些操作的时间复杂度可能会达到 O(n)。由于其高效的搜索特性,二叉搜索树常被用于实现关联数组和集合等数据结构。然而,为了避免树的结构不平衡导致性能下降,人们也发展了平衡二叉搜索树(如红黑树、AVL树)等变种。
2.0 二叉搜索树的成员变量及其构造方法
外部类成员变量有:根节点、节点类(内部类)。
外部类构造方法:默认的构造方法,对外公开二叉搜索树的核心方法。
节点类的成员变量有:
- key 关键字:相对比一般的二叉树,二叉搜索树可以明显提高增删查改的效率原因在于关键字,可以根据比较两个关键字的大小进行操作。
- value 值:作用则为存放值。
- left :链接左节点。
- right:链接右节点。
节点类的构造方法:
带两个参数的构造方法:参数为 key 、value
带四个参数的构造方法:参数为 key 、value 、left 、right
代码如下:
public class BinaryTree {BinaryNode root = null;static class BinaryNode {int key;Object value;BinaryNode left;BinaryNode right;public BinaryNode(int kty, Object value) {this.key = kty;this.value = value;}public BinaryNode(int key, Object value, BinaryNode left, BinaryNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}}
补充二叉搜索树在增、删、查、改的效率高的原因:
二叉搜索树的高效性与其关键字的特性密切相关。二叉搜索树的关键特性是,对于每个节点,其左子节点的值小于该节点的值,右子节点的值大于该节点的值。这种特性使得在二叉搜索树中进行搜索、插入和删除操作时,可以通过比较关键字的大小来快速定位目标节点,从而实现高效的操作。在平均情况下,这些操作的时间复杂度为 O(log n),其中 n 为树中节点的数量。因此,关键字的有序性是二叉搜索树能够实现高效操作的关键原因之一。
3.0 实现二叉树的核心接口
public interface BinarySearchTreeInterface {/***查找 key 对应的 value*/Object get(int key);/*** 查找最小关键字对应值*/Object min();/*** 查找最大关键字对应值*/Object max();/*** 存储关键字与对应值*/void put(int key, Object value);/*** 查找关键字的后驱*/Object successor(int key);/*** 查找关键字的前驱*/Object predecessor(int key);/*** 根据关键字删除*/Object delete(int key); }
3.1 实现二叉搜索树 - 获取值 get(int key)
实现思路为:从根节点开始,先判断当前的节点 p.key 与 key 进行比较,若 p.key > key,则向左子树下潜 p = p.left ;若 p.key < key ,则向右子树下潜 p = p.right ;若 p.key == key ,则找到到了关键字,返回该节点的值 p.value 。按这样的规则一直循环下去,直到 p == null 退出循环,则说明没有找到对应的节点,则返回 null 。
代码如下:
@Overridepublic Object get(int key) {if (root == null) {return null;}BinaryNode p = root;while(p != null) {if (p.key > key) {p = p.left;}else if (p.key < key) {p = p.right;}else {return p.value;}}return null;}若 root 为 null ,则不需要再进行下去了,直接结束。
3.2 实现二叉搜索树 - 获取最小的关键字 min(BinaryNode node)
实现思路:在某一个树中,需要得到最小的关键字,由根据数据结构的特点,最小的关键字在数的最左边,简单来说:一直向左子树遍历下去,直到 p.left == null 时,则该 p 节点就是最小的关键字了。然后找到了最小的节点,返回该节点的值即可。
代码如下:
非递归实现:
@Overridepublic Object min() {if (root == null) {return null;}BinaryNode p = root;while(p.left != null) {p = p.left;}return p.value;}//重载了一个方法,带参数的方法。public Object min(BinaryNode node) {if (node == null) {return null;}BinaryNode p = node;while (p.left != null) {p = p.left;}return p.value;}递归实现:
//使用递归实现找最小关键字public Object minRecursion() {return doMin(root);}private Object doMin(BinaryNode node) {if (node == null) {return null;}if (node.left == null) {return node.value;}return doMin(node.left);}
3.3 实现二叉搜索树 - 获取最大的关键字 max(BinaryNode node)
实现思路为:在某一个树中,需要得到最大的关键字,由根据数据结构的特点,最大的关键字在数的最右边,简单来说:一直向右子树遍历下去,直到 p.right == null 时,则该 p 节点就是最大的关键字了。然后找到了最大的节点,返回该节点的值即可。
代码如下:
非递归实现:
@Overridepublic Object max() {if (root == null) {return null;}BinaryNode p = root;while(p.right != null) {p = p.right;}return p.value;}//重载了一个带参数的方法public Object max(BinaryNode node) {if (node == null) {return null;}BinaryNode p = node;while (p.right != null) {p = p.right;}return p.value;}递归实现:
//使用递归实现找最大关键字public Object maxRecursion() {return doMax(root);}private Object doMax(BinaryNode node) {if (node == null) {return null;}if (node.right == null) {return node.value;}return doMax(node.right);}
3.4 实现二叉搜索树 - 增、更新 put( int key, Object value)
实现思路为:在二叉搜索树中先试着查找是否存在与 key 对应的节点 p.key 。若找到了,则为更新该值 p.value = value 即可。若找不到,则需要新增该关键字节点。
具体来分析如何新增关键字,先定义 BinaryNode parent 、 BinaryNode p,p 指针在去比较 key 之前,先让 parent 指向 p 。最后循环结束后, p == null ,对于 parent 来说,此时正指着 p 节点的双亲节点。 接着创建一个新的节点,BinaryNode newNode = new BinaryNode(key, value) ,则此时还需要考虑的是,该新的节点该连接到 parent 的左孩子还是右孩子 ?需要比较 parent.key 与 newNode.key 的大小即可,若 parent.key > newNode.key,则链接到 parent.left 处;若 prent.key < newNode.key ,则连接到 parent.right 处。
代码如下:
@Overridepublic void put(int key, Object value) {if (root == null) {root = new BinaryNode(key,value);return;}BinaryNode p = root;BinaryNode parent = null;while (p != null) {parent = p;if (p.key > key) {p = p.left;} else if (p.key < key) {p = p.right;}else {p.value = value;return;}}//该树没有该关键字,因此需要新建节点对象BinaryNode newNode = new BinaryNode(key,value);if (newNode.key < parent.key) {parent.left = newNode;}else {parent.right = newNode;}}
3.5 实现二叉搜索树 - 查找关键字的后驱节点 successor(int key)
具体实现思路为:先遍历找到该关键字的节点,若找不到,则返回 null ;若找到了,判断以下的两种情况,第一种情况:该节点有右子树,则该关键字的后驱为右子树的最小关键字;第二种情况:该节点没有右子树,则该关键字的后驱为从右向左而来的祖宗节点。最后返回该后驱节点的值
代码如下:
@Overridepublic Object successor(int key) {if (root == null) {return null;}//先找到该关键字节点BinaryNode p = root;BinaryNode sParent = null;while (p != null) {if (p.key > key) {sParent = p;p = p.left;} else if (p.key < key) {p = p.right;}else {break;}}//没有找到关键字的情况if (p == null) {return null;}//情况一:该节点存在右子树,则该后继为右子树的最小关键字if (p.right != null) {return min(p.right);}//情况二:该节点不存在右子树,那么该后继就需要到祖宗从右向左的节点if (sParent == null) {//可能不存在后继节点,比如最大关键字的节点就没有后继节点了return null;}return sParent.value;}
3.6 实现二叉搜索树 - 查找关键字的前驱节点 predecessor(int key)
具体实现思路为:先对该二叉树进行遍历寻找 key 的节点,若遍历结束还没找到,则返回 null ;若找到了,需要判断以下两种情况:
第一种情况:该节点有左子树,则该前驱节点为该左子树的最大关键字节点。
第二种情况:该节点没有左子树,则该前驱节点为从左向右而来的祖宗节点。
最后返回该前驱节点的值。
代码如下:
@Overridepublic Object predecessor(int key) {if (root == null) {return null;}BinaryNode p = root;BinaryNode sParent = null;while (p != null) {if (p.key > key) {p = p.left;} else if (p.key < key) {sParent = p;p = p.right;}else {break;}}if (p == null) {return null;}//情况一:存在左子树,则该前任就为左子树的最大关键字节点if (p.left != null) {return max(p.left);}//情况二:不存在左子树,则该前任为从祖宗自左向右而来的节点if (sParent == null) {return null;}return sParent.value;}
3.7 实现二叉搜索树 - 删除关键字节点 delete(int key)
具体实现思路为:先遍历二叉树,查找该关键字节点。若遍历结束了还没有找到,则返回 null ;若找到了,则需要以下四种情况:
第一种情况:找到该删除的节点只有左子树。则直接让该左子树 "托付" 给删除节点的双亲节点,这就删除了该节点了。至于左子树是链接到双亲节点的左边还有右边这个问题,根据该数据结构的特点,由该删除节点来决定。若删除的节点之前是链接该双亲节点的左边,则左子树也是链接到该双亲节点的左边;若删除的节点之前是链接该双亲节点的右边,则左子树也是链接到该双亲节点的右边。
第二种情况:找到该删除的节点只有右子树。则直接让该右子树 "托付" 给删除节点的双亲节点,这就删除了该节点了。至于右子树是链接到双亲节点的左边还有右边这个问题,根据该数据结构的特点,由该删除节点来决定。若删除的节点之前是链接该双亲节点的左边,则右子树也是链接到该双亲节点的左边;若删除的节点之前是链接该双亲节点的右边,则右子树也是链接到该双亲节点的右边。
第三种情况:找到该删除节点都没有左右子树。该情况可以归并到以上两种情况的任意一种处理均可。
第四种情况:找到该删除节点都有左右子树。分两步:第一步,先找后继节点来替换删除节点,找该后继节点直接到删除节点的右子树中找最小的关键字节点即可。第二步,需要先将后继节点的右子树处理好,需要将该右子树交给替换节点的双亲节点链接。还需要判断两种情况:第一种情况,若删除节点与替换节点是紧挨着的,对替换节点的右子树无需要求,只对左子树重新赋值;若删除节点与替换节点不是紧挨着的关系,对替换节点的左右子树都要重新赋值。
代码如下:
@Overridepublic Object delete(int key) {if (root == null) {return null;}BinaryNode p = root;BinaryNode parent = null;while (p != null) {if (p.key > key) {parent = p;p = p.left;} else if (p.key < key) {parent = p;p = p.right;}else {break;}}//没有找到该关键字的节点if (p == null) {return null;}//情况一、二、三:只有左子树或者右子树或者都没有if (p.right == null) {shift(parent,p,p.left);} else if (p.left == null) {shift(parent,p,p.right);}else {//情况四:有左右子树//替换节点采用删除节点的后继节点//先看被删的节点与替换的节点是否为紧挨在一起BinaryNode s = p.right;BinaryNode sParent = p;while (s.left != null) {sParent = s;s = s.left;}if (sParent != p) {//说明没有紧挨在一起,则需要将替换节点的右子树进行处理shift(sParent,s,s.right);s.right = p.right;}shift(parent,p,s);s.left = p.left;}return p.value;}private void shift(BinaryNode parent, BinaryNode delete, BinaryNode next) {if (parent == null) {root = next;} else if (parent.left == delete) {parent.left = next;}else if (parent.right == delete){parent.right = next;}}为了方便,将删除节点与替换节点之间的替换操作单独成一个方法出来。
递归实现删除关键字 key 节点,同理,也是细分为以上描述的四种情况。
代码如下:
//使用递归实现删除关键字节点public BinaryNode deleteRecursion(BinaryNode node , int key) {if (node == null) {return null;}if (node.key > key) {node.left = deleteRecursion(node.left,key);return node;} else if (node.key < key) {node.right = deleteRecursion(node.right,key);return node;}else {if (node.right == null) {return node.left;} else if (node.left == null) {return node.right;}else {BinaryNode s = node.right;while (s.left != null) {s = s.left;}s.right = deleteRecursion(node.right,s.key);s.left = node.left;return s;}}}
3.8 实现二叉搜索树 - 查找范围小于关键字的节点值 less(int key)
具体实现思路为:利用中序遍历,来遍历每一个节点的 key ,若小于 key 的节点,直接放到数组容器中;若大于 key 的,可以直接退出循环。最后返回该数组容器即可。
代码如下:
//找 < key 的所有 valuepublic List<Object> less(int key) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();BinaryNode p = root;Stack<BinaryNode> stack = new Stack<>();while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;}else {BinaryNode pop = stack.pop();if (pop.key < key) {result.add(pop.value);}else {break;}p = pop.right;}}return result;}
3.9 实现二叉搜索树 - 查找范围大于关键字的节点值 greater(int key)
具体实现思路:利用中序遍历,来遍历每一个节点的 key ,若大于 key 的节点,直接放到数组容器中。
代码如下:
//找 > key 的所有 valuepublic List<Object> greater(int key) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();Stack<BinaryNode> stack = new Stack<>();BinaryNode p = root;while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;}else {BinaryNode pop = stack.pop();if (pop.key > key) {result.add(pop.value);}p = pop.right;}}return result;}
该方法的改进:遍历方向进行调整,先从右子树开始,再访问根节点,最后才到左子树。因此只要小于 key 的关键字节点,直接退出循环。
代码如下:
//改进思路:遍历方向进行调整,先从右子树开始,再访问根节点,最后才到左子树public List<Object> greater1(int key) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();Stack<BinaryNode> stack = new Stack<>();BinaryNode p = root;while (p != null || !stack.isEmpty()) {if (p != null ) {stack.push(p);p = p.right;}else {BinaryNode pop = stack.pop();if (pop.key > key) {result.add(pop.value);}else {break;}p = pop.left;}}return result;}
4.0 实现二叉搜索树 - 查找范围大于 k1 且小于 k2 关键字的节点值 between(int k1, int k2)
实现思路跟以上的思路没有什么区别,唯一需要注意的是,当前节点的 key > k2 则可以退出循环了。
代码如下:
//找到 >= k1 且 =< k2 的所有valuepublic List<Object> between(int k1, int k2) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();Stack<BinaryNode> stack = new Stack<>();BinaryNode p = root;while(p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;}else {BinaryNode pop = stack.pop();if (pop.key >= k1 && pop.key <= k2) {result.add(pop.value);} else if (pop.key > k2) {break;}p = pop.right;}}return result;}
5.0 实现二叉搜索树核心方法的完整代码
实现接口代码:
import java.util.ArrayList;import java.util.List; import java.util.Stack;public class BinaryTree implements BinarySearchTreeInterface{BinaryNode root = null;static class BinaryNode {int key;Object value;BinaryNode left;BinaryNode right;public BinaryNode(int kty, Object value) {this.key = kty;this.value = value;}public BinaryNode(int key, Object value, BinaryNode left, BinaryNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}@Overridepublic Object get(int key) {if (root == null) {return null;}BinaryNode p = root;while(p != null) {if (p.key > key) {p = p.left;}else if (p.key < key) {p = p.right;}else {return p.value;}}return null;}@Overridepublic Object min() {if (root == null) {return null;}BinaryNode p = root;while(p.left != null) {p = p.left;}return p.value;}public Object min(BinaryNode node) {if (node == null) {return null;}BinaryNode p = node;while (p.left != null) {p = p.left;}return p.value;}//使用递归实现找最小关键字public Object minRecursion() {return doMin(root);}private Object doMin(BinaryNode node) {if (node == null) {return null;}if (node.left == null) {return node.value;}return doMin(node.left);}@Overridepublic Object max() {if (root == null) {return null;}BinaryNode p = root;while(p.right != null) {p = p.right;}return p.value;}public Object max(BinaryNode node) {if (node == null) {return null;}BinaryNode p = node;while (p.right != null) {p = p.right;}return p.value;}//使用递归实现找最大关键字public Object maxRecursion() {return doMax(root);}private Object doMax(BinaryNode node) {if (node == null) {return null;}if (node.right == null) {return node.value;}return doMax(node.right);}@Overridepublic void put(int key, Object value) {if (root == null) {root = new BinaryNode(key,value);return;}BinaryNode p = root;BinaryNode parent = null;while (p != null) {parent = p;if (p.key > key) {p = p.left;} else if (p.key < key) {p = p.right;}else {p.value = value;return;}}//该树没有该关键字,因此需要新建节点对象BinaryNode newNode = new BinaryNode(key,value);if (newNode.key < parent.key) {parent.left = newNode;}else {parent.right = newNode;}}@Overridepublic Object successor(int key) {if (root == null) {return null;}//先找到该关键字节点BinaryNode p = root;BinaryNode sParent = null;while (p != null) {if (p.key > key) {sParent = p;p = p.left;} else if (p.key < key) {p = p.right;}else {break;}}//没有找到关键字的情况if (p == null) {return null;}//情况一:该节点存在右子树,则该后继为右子树的最小关键字if (p.right != null) {return min(p.right);}//情况二:该节点不存在右子树,那么该后继就需要到祖宗从右向左的节点if (sParent == null) {//可能不存在后继节点,比如最大关键字的节点就没有后继节点了return null;}return sParent.value;}@Overridepublic Object predecessor(int key) {if (root == null) {return null;}BinaryNode p = root;BinaryNode sParent = null;while (p != null) {if (p.key > key) {p = p.left;} else if (p.key < key) {sParent = p;p = p.right;}else {break;}}if (p == null) {return null;}//情况一:存在左子树,则该前任就为左子树的最大关键字节点if (p.left != null) {return max(p.left);}//情况二:不存在左子树,则该前任为从祖宗自左向右而来的节点if (sParent == null) {return null;}return sParent.value;}@Overridepublic Object delete(int key) {if (root == null) {return null;}BinaryNode p = root;BinaryNode parent = null;while (p != null) {if (p.key > key) {parent = p;p = p.left;} else if (p.key < key) {parent = p;p = p.right;}else {break;}}//没有找到该关键字的节点if (p == null) {return null;}//情况一、二、三:只有左子树或者右子树或者都没有if (p.right == null) {shift(parent,p,p.left);} else if (p.left == null) {shift(parent,p,p.right);}else {//情况四:有左右子树//替换节点采用删除节点的后继节点//先看被删的节点与替换的节点是否为紧挨在一起BinaryNode s = p.right;BinaryNode sParent = p;while (s.left != null) {sParent = s;s = s.left;}if (sParent != p) {//说明没有紧挨在一起,则需要将替换节点的右子树进行处理shift(sParent,s,s.right);s.right = p.right;}shift(parent,p,s);s.left = p.left;}return p.value;}private void shift(BinaryNode parent, BinaryNode delete, BinaryNode next) {if (parent == null) {root = next;} else if (parent.left == delete) {parent.left = next;}else if (parent.right == delete){parent.right = next;}}//使用递归实现删除关键字节点public BinaryNode deleteRecursion(BinaryNode node , int key) {if (node == null) {return null;}if (node.key > key) {node.left = deleteRecursion(node.left,key);return node;} else if (node.key < key) {node.right = deleteRecursion(node.right,key);return node;}else {if (node.right == null) {return node.left;} else if (node.left == null) {return node.right;}else {BinaryNode s = node.right;while (s.left != null) {s = s.left;}s.right = deleteRecursion(node.right,s.key);s.left = node.left;return s;}}}//找 < key 的所有 valuepublic List<Object> less(int key) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();BinaryNode p = root;Stack<BinaryNode> stack = new Stack<>();while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;}else {BinaryNode pop = stack.pop();if (pop.key < key) {result.add(pop.value);}else {break;}p = pop.right;}}return result;}//找 > key 的所有 valuepublic List<Object> greater(int key) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();Stack<BinaryNode> stack = new Stack<>();BinaryNode p = root;while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;}else {BinaryNode pop = stack.pop();if (pop.key > key) {result.add(pop.value);}p = pop.right;}}return result;}//改进思路:遍历方向进行调整,先从右子树开始,再访问根节点,最后才到左子树public List<Object> greater1(int key) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();Stack<BinaryNode> stack = new Stack<>();BinaryNode p = root;while (p != null || !stack.isEmpty()) {if (p != null ) {stack.push(p);p = p.right;}else {BinaryNode pop = stack.pop();if (pop.key > key) {result.add(pop.value);}else {break;}p = pop.left;}}return result;}//找到 >= k1 且 =< k2 的所有valuepublic List<Object> between(int k1, int k2) {if (root == null) {return null;}ArrayList<Object> result = new ArrayList<>();Stack<BinaryNode> stack = new Stack<>();BinaryNode p = root;while(p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;}else {BinaryNode pop = stack.pop();if (pop.key >= k1 && pop.key <= k2) {result.add(pop.value);} else if (pop.key > k2) {break;}p = pop.right;}}return result;}}
相关文章:
Java 数据结构篇-实现二叉搜索树的核心方法
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 二叉搜索树的概述 2.0 二叉搜索树的成员变量及其构造方法 3.0 实现二叉树的核心接口 3.1 实现二叉搜索树 - 获取值 get(int key) 3.2 实现二叉搜索树 - 获取最小…...
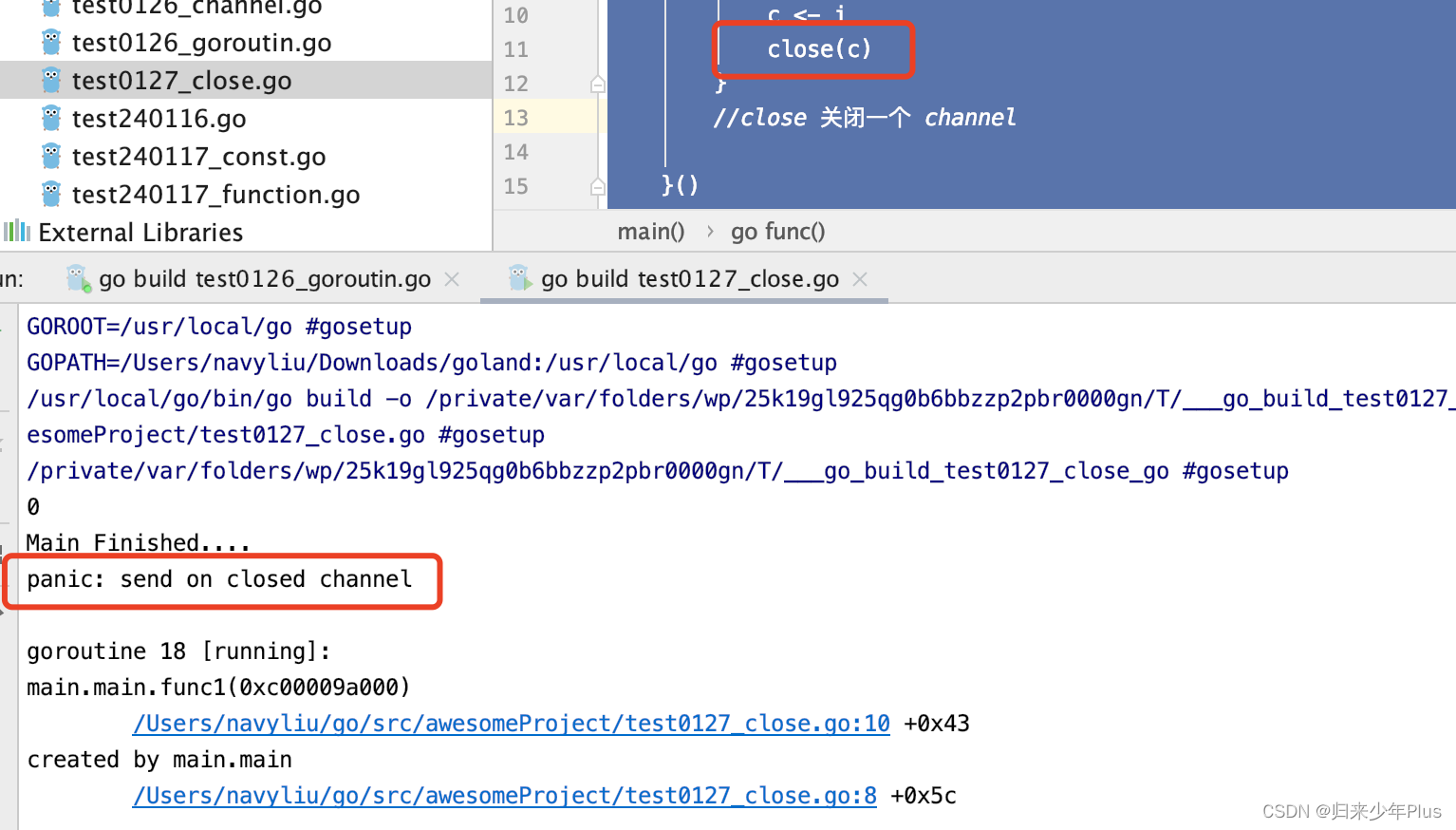
go语言(二十一)---- channel的关闭
channel不像文件一样需要经常去关闭,只有当你确实没有任何发送数据了,或者你想显示的结束range循环之类的,才去关闭channel。关闭channel后,无法向channel再发送数据,(引发pannic错误后,导致接收…...
【PyQt】01-PyQt下载
文章目录 前言静态库 一、PyQt是什么?二、安装1.Windows环境下安装安装PyQt5Designer 2.Liunx环境下安装 总结 前言 拜吾师 PyQt5 快速入门 静态库 补充一点知识: Windows: .lib Linux: .a .so(动态库) 简单描述PyQt就是python调用C的Qt文…...

不一样的味觉体验:精酿啤酒与烤肉的绝妙搭配
在繁华的都市生活中,人们总是在寻找那份与众不同的味觉享受。当夏日的微风轻轻拂过,你是否想过,与三五好友围坐在一起,拿着Fendi Club啤酒与烤肉的绝妙搭配,畅谈生活点滴,感受那份惬意与自在? F…...

linux系统ansible的jiaja2的语法和简单剧本编写
jianja2语法和简单剧本 jinja2语法Jinja default()设定if语句for语句 ansiblejiaja2的使用ansible目录结构:tasks目录下文件内容:nginx模板文件ansible变量文件ansible主playbook文件测试并执行:查看检测执行结果 剧本编写安装apache安装mysq…...

Three.js PBR 物理渲染
详解 Three.js PBR 物理渲染 Three.js 是一个流行的基于 WebGL 的 JavaScript 库,专门用于创建和运行三维动画和游戏。其中很关键的一部分是物理渲染(PBR)。本文将深入探讨 Three.js 的 PBR 渲染,并为初学者提供实用的指导。 什…...
POSIX(包含程序的可移植性) -- 详解
1. 什么是 POSIX 参考链接–知乎 POSIX 标准包含了进程管理、文件管理、网络通信、线程和同步、信号处理等方面的功能。 这些接口定义了函数、数据类型和常量等,为开发者提供了一个可移植的方法来与操作系统进行交互。 2. 谁遵守这个标准 遵守 POSIX 标准的主要是…...
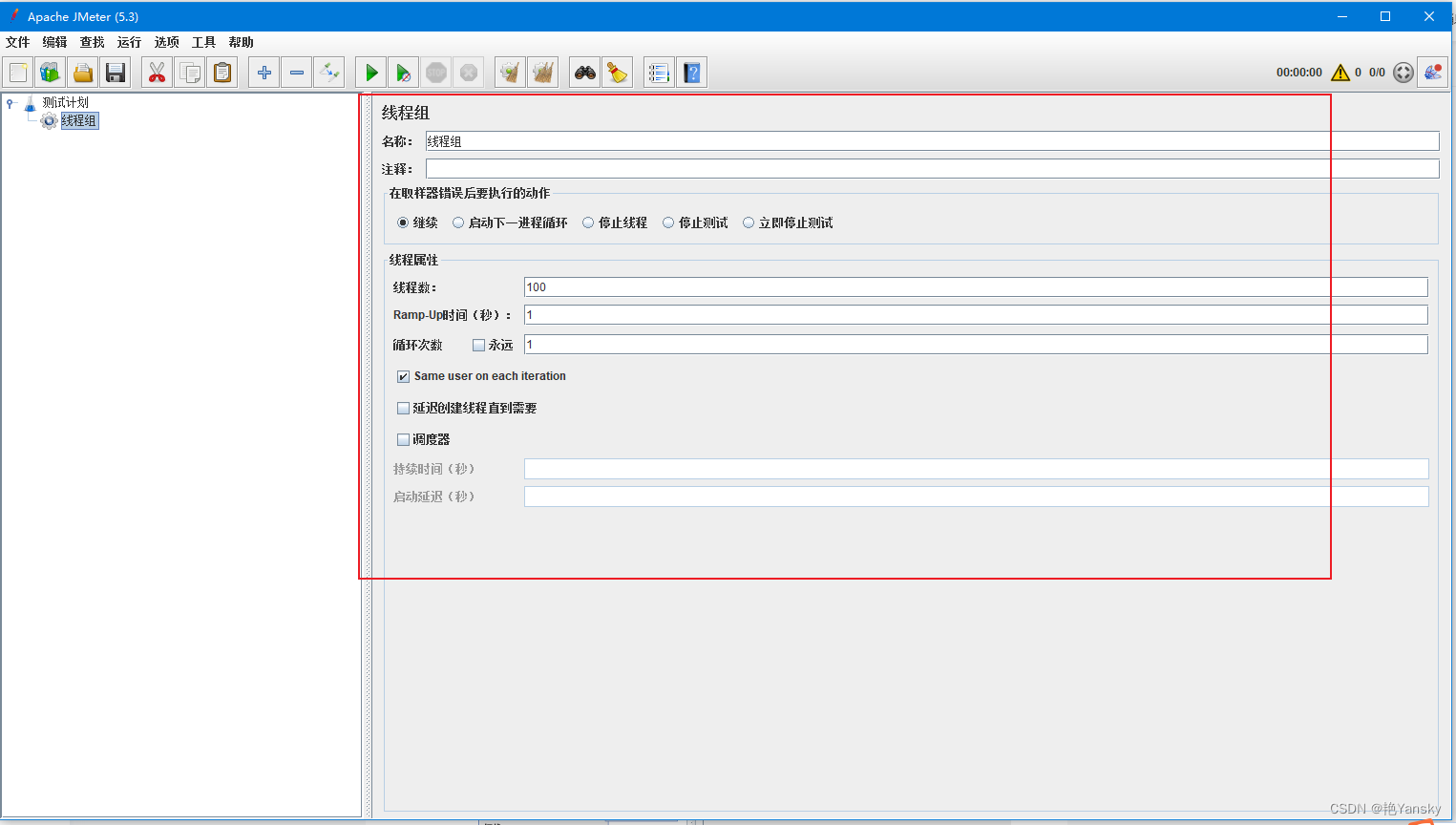
Jmeter学习系列之五:基础线程组(Thread Group)
前言 线程组是一系列线程的集合,每一个线程代表着一个正在使用应用程序的用户。在 jmeter 中,每个线程意味着模拟一个真实用户向服务器发起请求。 在 jmeter 中,线程组组件运行用户设置线程数量、初始化方式等等配置。 例如,如果你设置线程数为 100,那么 jmeter 将创建…...

Android 双卡适配 subId 相关方法
业务场景 双卡设备进行网络等业务时,需要正确操作对应的卡。 执行卡业务和主要是使用subId和 PhoneId/SlotId进行区分隔离。 代码举例 初始化subId //初始化subId private int mSubId SubscriptionManager.INVALID_SUBSCRIPTION_ID;//1、通过intent传值&#x…...
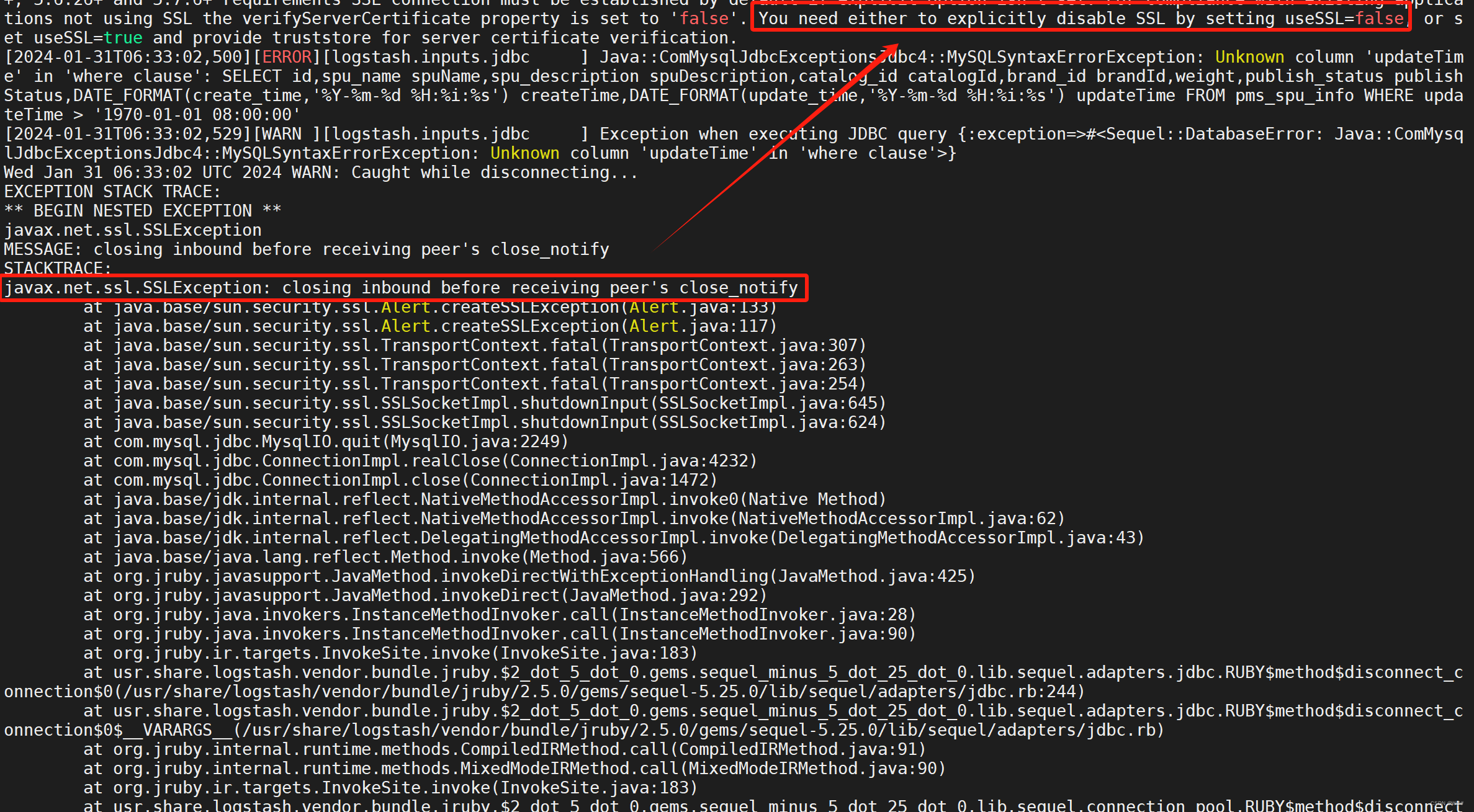
使用Logstash将MySQL中的数据同步至Elasticsearch
目录 1 使用docker安装ELK 1.1 安装Elasticsearch 1.2 安装Kibana 1.3 安装Logstash 2 数据同步 2.1 准备MySQL表和数据 2.2 运行Logstash 2.3 测试 3 Logstash报错(踩坑)记录 3.1 记录一 3.1.1 报错信息 3.1.2 报错原因 3.1.3 解决方案 3.2 记录二 3.2.1 报错信…...
 更新)
米贸搜|Facebook公共主页反馈分数(ACE) 更新
前段时间Meta改进了公共主页反馈分数的仪表板,发现有部分广告主似乎没有接受到这条动态,今天为大家整理出更新内容,方便各位广告主了解学习! Meta重新设计了公共主页反馈分数仪表板,以便广告主能更轻松地了解总体反馈…...

代码随想录算法训练营第三十七天| 738.单调递增的数字、968.监控二叉树
738.单调递增的数字 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 解题思路:一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然…...
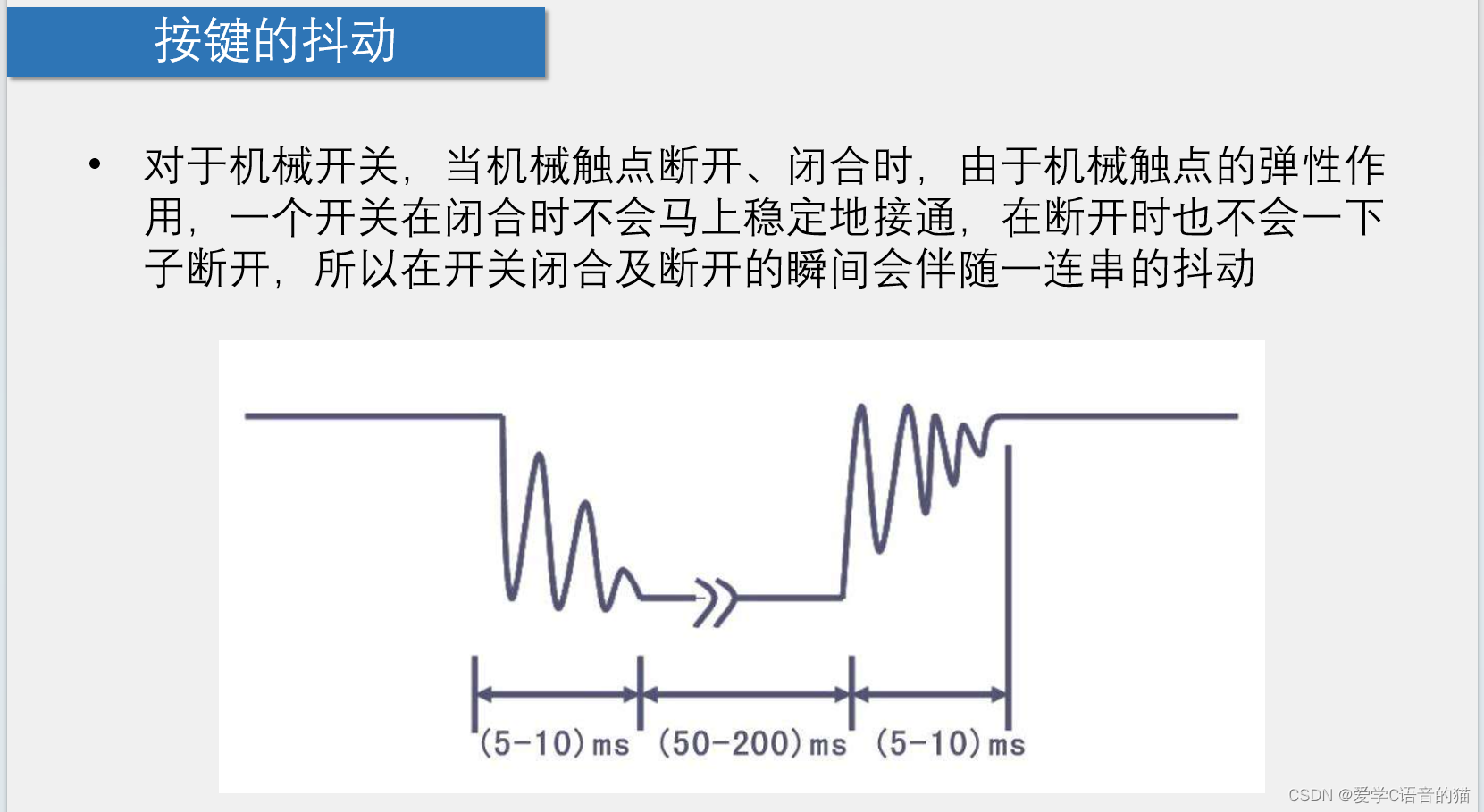
51单片机编程应用(C语言):独立按键
目录 1.独立按键介绍 2.独立按键控制LED亮灭 1.1按下时LED亮,松手LED灭(按一次执行亮灭) 1.2首先按下时无操作,松手时LED亮(再按下无操作,所以LED亮),松手LED灭(松手时…...
小程序定制开发前,应该考虑些什么?
引言 在移动互联网时代,小程序已经成为许多企业和个人推广业务、提供服务的理想平台。然而,在进行小程序定制开发之前,开发者和业务方需要细致入微地考虑一系列关键因素,以确保最终的小程序既能满足用户需求,又能够顺…...
2024/2/1学习记录
echarts 为柱条添加背景色: 若想设置折线图的点的样式,设置 series.itemStyle 指定填充颜色就好了,设置线的样式设置 lineStyle 就好了。 在折线图中倘若要设置空数据,用 - 表示即可,这对于其他系列的数据也是 适用的…...

10个React状态管理库推荐
本文将为您推荐十款实用的React状态管理库,帮助您打造出高效、可维护的前端应用。让我们一起看看这些库的魅力所在! 在前端开发中,状态管理是至关重要的一环。React作为一款流行的前端框架,其强大的状态管理功能备受开发者青睐。…...

从0开始写android
系列文章目录 文章目录 一、 从0开始实现 onCreate 的setContentView二、 从0 开始实现 onMeasure三、 从0 开始实现 onLayout四、 从0 开始实现 onDraw总结 前言 接上文,测量完View树的每个节点View的宽和高后,开始布局。 一、ViewRootImpl 的调用栈…...
使用pygame建立一个简单的使用键盘方向键移动的方块小游戏
import pygame import sys# 初始化pygame pygame.init()# 设置窗口大小 screen_size (640, 480) # 创建窗口 screen pygame.display.set_mode(screen_size) # 设置窗口标题 pygame.display.set_caption("使用键盘方向键移动的方块的简单小游戏")# 设置颜色 bg_colo…...

从零开始:CentOS系统下搭建DNS服务器的详细教程
前言 如果你希望在CentOS系统上建立自己的DNS服务器,那么这篇文章绝对是你不容错过的宝藏指南。我们提供了详尽的步骤和实用技巧,让你能够轻松完成搭建过程。从安装必要的软件到配置区域文件,我们都将一一为你呈现。无论你的身份是运维人员,还是程序员,抑或是对网络基础设…...

2024美赛B题解析:寻找潜水器Searching for Submersibles
解析:传送门 Maritime Cruises Mini-Submarines (MCMS) 是一家总部位于希腊的公司,负责建造潜水器 能够将人类带到海洋的最深处。潜水器被移动到 位置和部署不受主机船的束缚。MCMS现在希望使用他们的潜水器 带领游客冒险探索爱奥…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
