C++之平衡二叉搜索树查找

个人主页:[PingdiGuo_guo]
收录专栏:[C++干货专栏]
大家好,我是PingdiGuo,今天我们来学习平衡二叉搜索树查找。
目录
1.什么是二叉树
2.什么是二叉搜索树
3.什么是平衡二叉搜索树查找
4.如何使用平衡二叉搜索树查找
5.平衡二叉搜索树查找的用处
6.平衡二叉搜索树查找适合解决什么样的问题
7.注意事项
8.总结
1.什么是二叉树
二叉树(Binary Tree)是一种基本的数据结构,它是由n(n≥0)个节点组成的有限集合。在二叉树中,每个节点最多含有两个子节点,分别称为左子节点(left child)和右子节点(right child)。根据节点的连接方式和节点间的关系,二叉树可以有不同的形态和用途。
以下是二叉树的一些关键特性:
1.根节点(Root Node):二叉树中的顶级节点,没有父节点。

2.叶节点(Leaf Node / Terminal Node):没有子节点的节点。
3.内部节点(Internal Node):至少有一个子节点的节点。

4.空(或空树):没有任何节点的二叉树。

5.二叉树的层级:从根开始算起,每一层包含的节点数量可以从1开始递增。
二叉树按照节点间的特定关系还可以进一步分类,比如:
- 满二叉树 (Full Binary Tree):除了叶子节点外,每个节点都有两个子节点,且所有叶子节点都在最后一层。

- 完全二叉树 (Complete Binary Tree):除了最后一层外,每一层都被完全填满,且最后一层的所有节点都尽可能地靠左排列。
- 二叉搜索树 (Binary Search Tree, BST):对于树中的任意节点,其左子树中所有节点的值小于该节点的值,而右子树中所有节点的值大于该节点的值。
而我们要学习的平衡二叉搜索树查找,就是在二叉搜索树之上的一种算法。
2.什么是二叉搜索树
二叉搜索树(Binary Search Tree, BST)是一种特定数据结构。在二叉搜索树中,每个节点包含一个键(key)及其关联的值,且满足以下特性:
1. 每个节点的键大于其左子树中任意节点的键。
2. 每个节点的键小于其右子树中任意节点的键。
3. 左右子树也各自遵循相同的规则。

3.什么是平衡二叉搜索树查找
在了解平衡二叉搜索树查找之前,我们需要先来了解什么是二叉搜索树查找。
1. BST查找(二叉搜索树查找):
- BST是一种基本的二叉树结构,它满足以下性质:
- 左子树上的所有节点的值都小于根节点的值。
- 右子树上的所有节点的值都大于根节点的值。
- 左右子树也分别为BST。
- 查找效率取决于树的形状。在最坏情况下,如果BST退化成链状结构(所有节点的左子树为空或右子树为空),查找的时间复杂度会达到O(n),其中n为树中节点的数量。
- 优点:对于有序数据,查找、插入和删除的平均时间复杂度都是O(log n);易于实现且直观。
链状结构:

2. 平衡二叉搜索树查找:
- 平衡二叉搜索树是一种具备自动平衡性的二叉搜索树,其中最常见的是AVL树和红黑树。
- 平衡二叉搜索树通过特定的平衡调整操作,例如旋转和调整节点的平衡因子,来保持树的平衡性。
- 查找、插入和删除操作的最坏时间复杂度均被保证为O(log n),提升了性能的稳定性。
- 在大规模数据处理中,通过自平衡机制避免了极端情况下的性能下降。
- 平衡二叉搜索树相比于BST,实现更为复杂,需要考虑平衡调整操作和存储平衡因子,但能提供更稳定的查找性能。
总结来说,平衡二叉搜索树相比于普通的二叉搜索树能够提供更稳定的查找性能,并且适用于需要频繁插入和删除操作的场景。但它的实现要比BST复杂一些。在一些简单的应用场景中,BST也能满足要求,并且实现更简单。选择使用哪种树结构取决于具体需求和性能要求。
AVL树:

查找步骤:
1. 从根节点开始。
2. 比较当前节点的值与目标值的大小关系。
- 如果目标值等于当前节点的值,则查找结束,找到目标节点。
- 如果目标值小于当前节点的值,则递归地在当前节点的左子树中查找。
- 如果目标值大于当前节点的值,则递归地在当前节点的右子树中查找。
3. 重复步骤2,直到找到目标节点或者遍历到空节点为止。
示例:
假设我们有一个AVL树如下所示(以括号形式表示节点及其左右子树,其中数字代表节点值):
5
/ \
3 7
/ \ \
2 4 8
现在我们要查找值为4的节点:
- 首先从根节点5开始查找。
- 因为4小于5,所以我们移动到左子树(节点3)。
- 接着比较4和3,因为4大于3,所以移动到节点3的右子树(节点4)。
- 发现节点4的值正好等于目标值4,查找结束。
因此,在这个例子中,我们成功找到了值为4的节点。在整个查找过程中,我们只需要经过两次比较就找到了目标节点,这正是AVL树高效查找能力的体现。
查找思想:
二叉搜索树的核心思想是“有序性”,即对于任意节点而言,其左子树中的所有节点值都小于该节点值,右子树中的所有节点值都大于该节点值。因此,查找过程可以通过比较节点值快速缩小查找范围,时间复杂度理论上可以达到O(log n),其中n是树中节点的数量。
为何需要引入平衡性质?
尽管二叉搜索树具有较好的查找性能,但如果树的形状严重偏离平衡,比如变为链状结构,那么查找最坏情况下的时间复杂度会退化为O(n)。为了确保查找、插入和删除等操作的时间复杂度始终维持在接近O(log n)的水平,我们需要对二叉搜索树添加自平衡机制,这就是平衡二叉搜索树的设计初衷。
4.如何使用平衡二叉搜索树查找
1. 导入相应的头文件,如#include <set>或#include <map>,这些头文件中已经实现了平衡二叉搜索树。
2. 定义相应的平衡二叉搜索树对象,例如std::set<int>或std::map<int, std::string>。
3. 使用插入操作将数据插入到平衡二叉搜索树中,例如使用insert方法,如set.insert(value)或map.insert(std::make_pair(key, value))。
4. 使用find方法进行查找操作,找到指定的值或键,并返回对应的迭代器。
5. 对于map类型的平衡二叉搜索树,你可以通过迭代器访问其键值对,例如iter->first代表键,iter->second代表值。
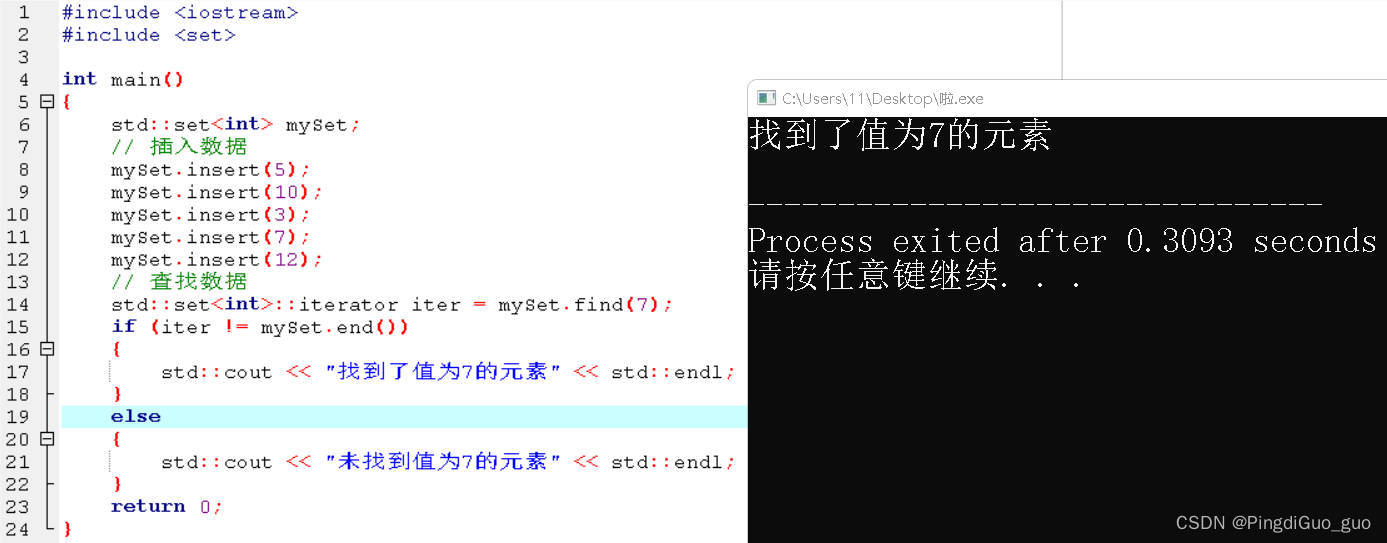
以下是一个简单的示例代码:
#include <iostream>
#include <set>int main() {std::set<int> mySet;// 插入数据mySet.insert(5);mySet.insert(10);mySet.insert(3);mySet.insert(7);mySet.insert(12);// 查找数据std::set<int>::iterator iter = mySet.find(7);if (iter != mySet.end()) {std::cout << "找到了值为7的元素" << std::endl;} else {std::cout << "未找到值为7的元素" << std::endl;}return 0;
}在上述代码中,我们使用std::set来创建一个平衡二叉搜索树,并插入了一些数据。然后,我们使用find方法来查找值为7的元素。最后,根据查找结果输出相应的提示信息。
5.平衡二叉搜索树查找的用处
平衡二叉搜索树在C++中的查找操作有以下几个用途:
1. 快速搜索:平衡二叉搜索树具有较快的查找速度,时间复杂度为O(log n),其中n为树中节点的数量。这使得它非常适合用于大量数据的快速搜索,特别是在需要频繁进行查找操作的情况下。
2. 排序:平衡二叉搜索树保持元素的有序性。它会自动根据元素的大小进行排序,因此可以很方便地进行有序的遍历和操作。
3. 唯一性:平衡二叉搜索树不允许元素的重复插入。这意味着你可以很容易地检查并避免重复的数据。
4. 范围查找:平衡二叉搜索树支持范围查找操作。你可以通过指定一个范围,查找树中满足范围条件的元素。
5. 插入和删除的平衡性:平衡二叉搜索树会在插入和删除操作后自动进行平衡,保持树的平衡性。这意味着即使进行了频繁的插入和删除操作,树的结构仍然是平衡的,这对于保持查找效率非常重要。
总而言之,平衡二叉搜索树在C++中的查找操作非常有用,特别是在需要快速搜索、排序和唯一性检查的场景下。它提供了高效的查找和操作性能,同时还能保持树的平衡性。
6.平衡二叉搜索树查找适合解决什么样的问题
平衡二叉搜索树查找适合解决需要高效查找操作的问题,特别是在数据量较大且需要频繁进行查找的情况下。以下是一些适合使用平衡二叉搜索树查找的问题:
1. 数据库系统:平衡二叉搜索树可以用于实现数据库的索引结构,快速查找满足某个条件的数据记录。
2. 字典/词典:平衡二叉搜索树可以用于实现字典或词典,存储单词及其对应的定义,可以快速查找某个单词的定义。
3. 路由表:平衡二叉搜索树可以用于路由表的设计,在网络路由中快速找到对应的目标地址。
4. 排名和统计:平衡二叉搜索树可以用于统计数据中的最大/最小值、中位数等,也可以根据某个值的排名进行查找。
总之,平衡二叉搜索树查找适合解决需要高效查找操作的问题,特别是在动态数据集合中需要频繁插入、删除和查找操作的场景下,可以提供较好的性能和效率。
7.注意事项
在使用平衡二叉搜索树时,有一些注意事项,特别是在C++中,以下是需要注意的几点:
1. 实现细节:平衡二叉搜索树的实现需要注意各种平衡因子的计算和旋转操作的正确性。在实现过程中,可以使用AVL树、红黑树等常见的平衡二叉搜索树的实现方法。
2. 内存管理:在动态分配节点内存时,需要注意正确释放节点的内存,以避免内存泄漏。可以使用智能指针来管理节点的内存,或者采用手动管理内存的方式。
3. 操作复杂度:平衡二叉搜索树的插入、删除和查找操作的平均时间复杂度为O(log n),但最坏情况下可能退化为O(n)。为了避免这种情况,需要正确实现平衡因子的维护和旋转操作。
4. 迭代器遍历:平衡二叉搜索树可以通过迭代器进行遍历操作,但需要确保迭代器的正确性。在进行插入、删除操作时,需要更新迭代器的位置。
5. 自定义比较函数:在C++中,可以通过实现自定义的比较函数来定义节点的排序规则。这对于存储自定义类型的数据结构非常有用。
6. 并发访问:如果多个线程同时访问和修改同一个平衡二叉搜索树,需要考虑并发访问的问题。可以采用锁机制来保证数据的一致性和安全性。
总之,在使用平衡二叉搜索树时,需要确保正确实现平衡因子的维护和旋转操作,注意内存管理和操作复杂度,同时考虑迭代器遍历和自定义比较函数的使用,以及并发访问的问题。
8.总结
本篇博客到这里就结束了,感谢大家的支持与观看,如果有好的建议欢迎留言,谢谢大家啦!
相关文章:

C++之平衡二叉搜索树查找
个人主页:[PingdiGuo_guo] 收录专栏:[C干货专栏] 大家好,我是PingdiGuo,今天我们来学习平衡二叉搜索树查找。 目录 1.什么是二叉树 2.什么是二叉搜索树 3.什么是平衡二叉搜索树查找 4.如何使用平衡二叉搜索树查找 5.平衡二叉…...
如何将Mac连接到以太网?这里有详细步骤
在Wi-Fi成为最流行、最简单的互联网连接方式之前,每台Mac和电脑都使用以太网电缆连接。这是Mac可用端口的标准功能。 如何将Mac连接到以太网 如果你的Mac有以太网端口,则需要以太网电缆: 1、将电缆一端接入互联网端口(可以在墙…...
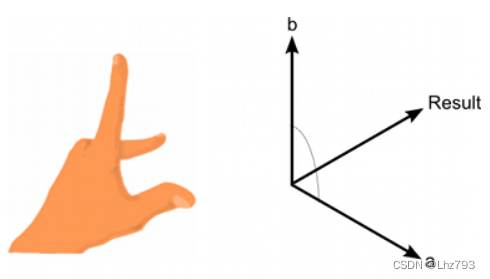
Unity点乘和叉乘
目录 前言 点乘 一、点乘是什么? 二、应用 三、使用步骤 1.代码示例 叉乘 一、叉乘是什么? 二、应用 三、使用步骤 1.代码示例 总结 前言 Unity中经常会用到向量的运算来计算目标的方位,朝向,角度等相关数据࿰…...

【ACL 2023】Enhancing Document-level EAE with Contextual Clues and Role Relevance
【ACL 2023】Enhancing Document-level Event Argument Extraction with Contextual Clues and Role Relevance 论文:https://aclanthology.org/2023.findings-acl.817/ 代码:https://github.com/LWL-cpu/SCPRG-master Abstract 与句子级推理相比&…...
Vue ECharts X轴 type为value的数据格式 + X轴固定间隔并向上取整十位数 - 附完整示例
ECharts:一个基于 JavaScript 的开源可视化图表库。 目录 效果 一、介绍 1、官方文档:Apache ECharts 2、官方示例 二、准备工作 1、安装依赖包 2、示例版本 三、使用步骤 1、在单页面引入 echarts 2、指定容器并设置容器宽高 3、数据处理&am…...
)
统计成绩(c++题解)
题目描述 半期考试结束了,几多欢喜几多愁!作为竞赛的选手,迟早是要经历大风大浪的,这点小小的涟漪无须太在意。但是对于成绩,还是要好好的分析一下的。 有N个学生,每个学生的数据包括学号、姓名、3门课的…...

【Qt】—— Hello World程序的实现
目录 (一)使⽤"按钮"实现 1.1 纯代码方式实现 1.2 可视化操作实现 (二)使⽤"标签"实现 2.1 纯代码方式实现 2.2 可视化操作实现 (一)使⽤"按钮"实现 1.1 纯代码方式实…...

谷歌浏览器网站打不开,显示叹号
问题: 您与此网站之间建立的连接不安全请勿在此网站上输入任何敏感信息(例如密码或信用卡信息),因为攻击者可能会盗取这些信息。 了解详情 解决方式: 网上有很多原因,亲测为DNS问题,设置&…...

怎么去除图片中不需要的部分?这三种高效方法快来试一下
在数字图像处理的浩瀚世界中,去除图片中不必要部分的任务,宛如一幅细致的画卷,需精心描绘。这些不必要部分,可能是背景、水印、无关紧要物体或错误部分,它们如同图片中的瑕疵,需要被巧妙地修饰或去除。这不…...

yolov5导出onnx模型问题
为了适配C工程代码,我在导出onnx模型时,会把models/yolo.py里面的forward函数改成下面这样, #转模型def forward(self, x):z [] # inference outputfor i in range(self.nl):x[i] self.m[i](x[i]) # convbs, _, ny, nx x[i].shape # x(…...
JS第一课简单看看这是啥东西
1.什么是JavaScript JS是一门编程语言,是一种运行在客户端(浏览器)的编程语言,主要是让前端的画面动起来,注意HTML和CSS不是编程语言,他俩是一种标记语言。JS只要有浏览器就能运行不用跟Python或者Java一样上来装一个jdk或者Pyth…...

2023年常用网络安全政策标准整合
文章目录 前言一、政策篇(一)等级保护(二)关键信息基础设施保护(三)数据安全(四)数据出境安全评估(五)网络信息安全(六)应急响应(七)网络安全专用产品检测认证制度(八)个人信息保护(九)商用密码二、标准篇前言 2023年,国家网络安全政策和标准密集发布,逐渐…...
Redis -- 背景知识
“知识就是力量” -- 弗朗西斯培根 目录 特性 为啥Redis快? 应用场景 Redis不能做什么? Redis是在内存中存储数据的一个中间件,用作为数据库,也可以用作为缓存,在分布式中有很高的威望。 特性 In-memory data structures&…...
如何在Shopee平台上进行手机类目选品?
在Shopee平台上进行手机类目的选品是一个关键而复杂的任务。卖家需要经过一系列的策略和步骤,以确保选品的成功和销售业绩的提升。下面将介绍一些有效的策略,帮助卖家在Shopee平台上进行手机类目选品。 先给大家推荐一款shopee知虾数据运营工具知虾免费…...

班级管理神器,教师在线发布系统
现如今,班级管理也需要与时俱进。传统的管理方式不仅效率低下,而且容易出错。为了更好地管理班级,教师需要一个强大的工具来帮助他们发布信息和管理学生。 发布系统是一款专门为教师设计的数字化管理工具。通过系统,老师们就可以…...

【Spring Boot 3】异步线程任务
【Spring Boot 3】异步线程任务 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是要花费或多或…...

JAVA斗地主逻辑-控制台版
未排序版: 准备牌->洗牌 -> 发牌 -> 看牌: App程序入口: package doudihzu01;public class App {public static void main(String[] args) {/*作为斗地主程序入口这里不写代码逻辑*///无参创建对象,作为程序启动new PokerGame();…...
Harmony的自定义组件和Page的数据同步
在开发过程中会经常使用自定义组件,就会遇到一个问题,在页面中引入组件后,如何把改变的值传递到自定义组件中呢,这就用到了装饰器,在这是单向传递的,用的装饰器是@State和@Prop @State在page页面中监听数据的变化 @Prop在自定义组件中监听page页面传递过来的变化值,并赋…...

【Vue3+Vite】路由机制router 快速学习 第四期
文章目录 路由简介路由是什么路由的作用 一、路由入门案例1. 创建项目 导入路由依赖2. 准备页面和组件3. 准备路由配置4. main.js引入router配置 二、路由重定向三、编程式路由(useRouter)四、路由传参(useRoute)五、路由守卫总结 路由简介 路由是什么 路由就是根据不同的 URL…...

python脚本实现浏览器驱动chromedriver的版本自动升级
chromedriver的版本号与chrome浏览器版本不匹配时在运行程序时就会报错 用下面的脚本可以自动安装chromedriver的最新版本到指定路径 from webdriver_manager.utils import get_browser_version_from_os from webdriver_manager.chrome import ChromeDriverManager import re…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
