18、多维图形绘制
目录
一、三维图形绘制
(一)曲线图绘制plot3()
(二)网格图绘制 mesh()
(三)曲面图绘制 surf()
(四)光照模型 surfl()
(五)等值线图(等高线图)绘制 contour()
四、四维图形可视化
(一)用颜色描述第四维
(二)其他函数
一、三维图形绘制
(一)曲线图绘制plot3()
在三维图形指令中,plot3指令与plot指令类似,其调用格式如下:
- plot3(X,Y,Z):X、Y、Z为同维向量时,绘制以X、Y、Z为x、y、z坐标的三维曲线;X、Y、Z为同维矩阵时,用X、Y、Z的对应列元素绘制x、y、z坐标的三维曲线,曲线的条数为矩阵的列数。
- plot3(X1,Y1,Z1,X2,Y2,Z2):绘制以X1、Y1、Z1和X2、Y2、Z2为x、y、z坐标的三维曲线。
- plot3(X,Y,Z,'PropertyName',PropertyValue,...):在PropertyName所规定的曲线属性下,绘制以X、Y、Z为x、y、z坐标的三维曲线。
- plot3(X1,Y1,Z1,'PropertyName1',PropertyValue1,X2,Y2,Z2,'PropertyName2',ProperValue2):在 PropertyName1所规定的曲线属性下,绘制以 X1、Y1、Z1为 x、y、z坐标的三维曲线;在PropertyName2所规定的曲线属性下,绘制以X2、Y2、Z2为x、y、z坐标的三维曲线。需要说明的是,plot3指令用来表现的是单参数的三维曲线,而非双参数的三维曲面。
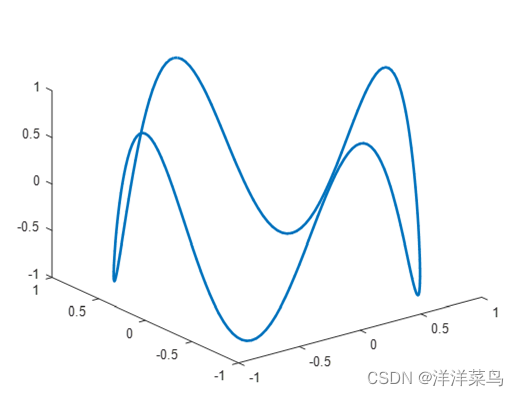
例1:plot3指令使用示例
clear;
clc;
theta=0:0.01*pi:pi*2;
x=sin(theta);
y=cos(theta);
z=cos(4*theta);
figure
plot3(x,y,z,'LineWidth',2);hold on;
运行结果:
(二)网格图绘制 mesh()
三维网格图和曲面图的绘制比三维曲线图更复杂,主要是因为绘图数据的准备及三维图形的色彩、明暗、光照和视角等的处理。
绘制函数z=f(x,y)的三维网格图的过程如下:
(1)确定自变量x和y的取值范围和取值间隔

(2)构成xoy平面上的自变量采样“格点”矩阵。
①利用“格点”矩阵的原理生成矩阵。

②利用meshgrid指令生成“格点”矩阵。
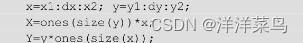
(3)计算在自变量采样“格点”上的函数值:Z=f(X,Y)。
绘制网格图的基本mesh指令的调用格式如下:
- mesh(X,Y,Z):以X为x轴自变量、Y为y轴自变量,绘制网格图;X、Y均为向量,若X、Y长度分别为m、n,则Z为m×n的矩阵,即[m,n]=size(Z),则网格线的顶点为(Xj,Yi,Zij)。
- mesh(Z):以Z矩阵列下标为x轴自变量、行下标为y轴自变量,绘制网格图。
- mesh(X,Y,Z,C):以X为x轴自变量、Y为y轴自变量,绘制网格图;其中C用于定义颜色,如果不定义 C,则成为 mesh(X,Y,Z),其绘制的网格图的颜色随着 Z 值的变化(即曲面高度)而变化。
- mesh(X,Y,Z,'PropertyName ',PropertyValue,...):以X为x轴自变量、Y为y轴自变量,绘制网格图;PropertyValue用来定义网格图的标记等属性。
例2:mesh指令使用示例
clear;
clc;
x=-10:0.1:10;y=-10:0.1:10;
[x,y]=meshgrid(x,y);
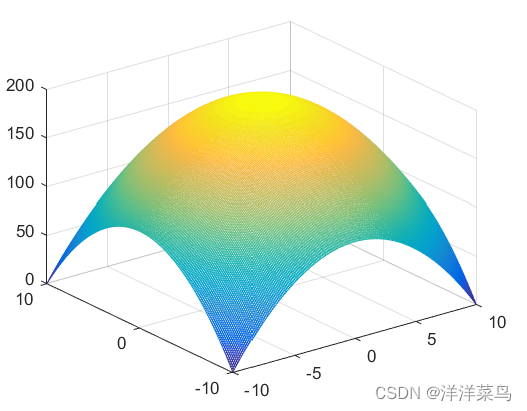
z=-x.^2-y.^2+200;
mesh(x,y,z)
运行结果:
(三)曲面图绘制 surf()
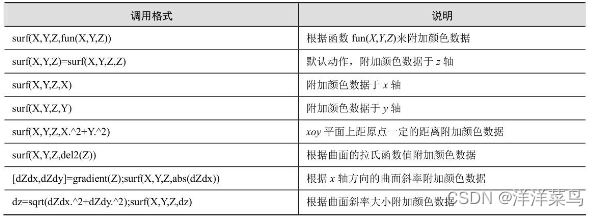
曲面图的绘制由surf指令完成,该指令的调用格式与mesh指令类似,具体如下:
- surf (X,Y,Z)。
- surf (Z)。
- surf (X,Y,Z,C)。
- surf(X,Y,Z,'PropertyName',PropertyValue,...)。
mesh指令所绘制的图形是网格划分的曲面图,而surf指令绘制得到的是平滑着色的三维曲面图,着色的方式是在得到相应的网格点后,对每一个网格依据该网格所代表的节点的色值(由变量C控制)来定义这一网格的颜色。
例3:surf指令与mesh指令对比
clear;
clc;
[x,y,z]=peaks(25);
figure
subplot(1,2,1);surf(x,y,z)
subplot(1,2,2);mesh(x,y,z)
运行结果:

(四)光照模型 surfl()
光照是一种利用方向光源来照亮物体的技术。在某些情况下,这项技术能使表面微妙的差异更容易看到,光照也可以增强三维图像的现实感
例4:带光照的曲面图
clear;
clc;
x=-10:0.1:10;y=-10:0.1:10;
[x,y]=meshgrid(x,y);
z=-x.^2-y.^2+200;
figure
surf(x,y,z,'FaceColor','r','EdgeColor','none');
camlight left;lighting phong
view(-15,65)
运行结果:
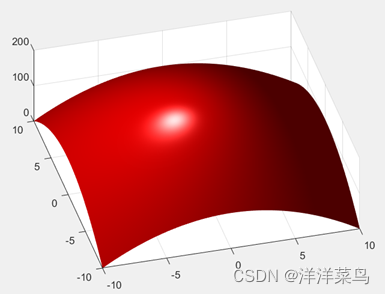
本例中将曲面涂上了红色,并且将surf指令所定义的网格线移除。同时,一个发光的物体被加到了“镜头”的左边(即从空间观看时所在表面的位置)。增加光源和设置好照明方式到phong后,使用view命令去改变视角,从空间的另一个不同的点再观看表面(方位角-15°和仰角65°)。最后,用工具栏缩放方式放大外观。
基于运用漫射、镜面反光和环境照明模型,MATLAB中还内置了surfl函数,可以画出类似于函数surf产生的带彩色的曲面。使用一个单色颜色映像(如灰色、纯白、铜黄或粉红色)和插值色彩,会画出效果更好的曲面。其调用格式如下:
surfl(X,Y,Z,S):其中S以[Sx,Sy,Sz]或[az,el]的形式定义光源方向。
在没有明确定义的情况下,其默认光源是逆时针45°。
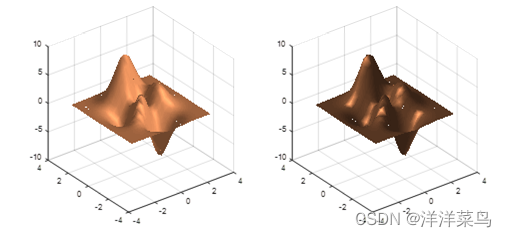
例5:surfl指令应用示例
clear;
clc;
[x,y,z]=peaks(25);
figure
subplot(1,2,1);surfl(x,y,z),colormap(copper),shading interp
subplot(1,2,2);surfl(x,y,z,[-90 30],[0.55 0.6 2 10]),shading interp
运行结果:
(五)等值线图(等高线图)绘制 contour()
绘制等值线图需要用到contour指令,其调用格式如下:
- contour(Z) 以Z矩阵的列下标为x轴自变量、行下标为y轴自变量,绘制等值线图
- contour(Z,n) n为所绘制的图形等值线的条数
- contour(Z,v) v为向量,向量长度为等值线的条数,并且等值线的值为对应的向量的元素值
- contour(X,Y,Z) 以X为x轴自变量、Y为y轴自变量,绘制等值线XY均为向量,若X、Y长度分别为m、n,则Z为m*n的矩阵,即[m,n]]=size(Z),网格线的顶点为(X(j),Y(i),Z(i,j))
- contour(X,Y,Z,n):其中n为所绘制的图形等值线的条数。
- contour(X,Y,Z,v):其中v为向量,向量的长度为等值线的条数,并且等值线的值为对应的向量的元素值。
- surf(...,LineSpec):其中LineSpec用来定义等值线的线型。
与contour作用相类似的指令还有contourf指令,其调用格式与contour相同。
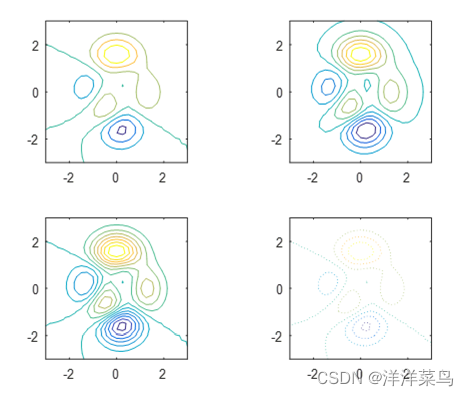
例6:contour指令使用示例
clear;
clc;
[x,y,z]=peaks(25);
figure
subplot(2,2,1);contour(x,y,z);axis square
subplot(2,2,2);contour(x,y,z,10);axis square
subplot(2,2,3);contour(x,y,z,-10:1:10);axis square
subplot(2,2,4);contour(x,y,z,':');axis square
运行结果:
四、四维图形可视化
(一)用颜色描述第四维
用mesh和surf等指令所绘制的图像,在未给出颜色参量的情况下,图像的颜色是沿着z轴的数据变化的。将颜色施加于z轴能够产生色彩亮丽的图画,但由于z轴已经存在,因此它并不提供新的信息。但使用颜色来描述不受3个轴影响的数据的某些属性,需要赋给三维作图函数的颜色参量所需要的“第四维”的数据。
如果作图函数的颜色参量是一个向量或矩阵,那么就用作颜色映像的下标。这个参量可以是任何实向量或与其参量维数相同的矩阵。
例7:使用颜色描述第四维示例
clear;
clc;
[x,y,z]=peaks(25);
r=sqrt(x.^2+y.^2)
figure
subplot(1,2,1);surf(x,y,z,z);axis tight
subplot(1,2,2);surf(x,y,z,r);axis tight
运行结果:
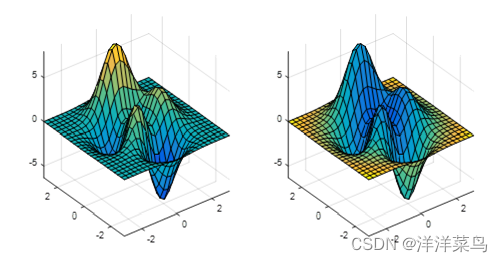
其中,在坐标系中描述一个面需要三维数据,而另一维数据描述空间中的点的坐标值,则使用不同的颜色表现出来;在左图中,第四维数据为Z;在右图中,第四维数据为R;在图上可以看到两者的颜色分布发生了明显的变化。
(二)其他函数
除了上述的函数,slice函数也可以通过颜色来表示存在于第四维空间中的值,其调用格式如下:
- slice(V,nx,ny,nz):显示三元函数V(X,Y,Z)确定的立体图在x轴、y轴、z轴方向上的若干点(对应若干平面)的切片图,各点的坐标由数量向量sx、sy、sz指定。其中V为大小为m×n×p的三维数组,默认值为X=1:m、Y=1:n、Z=1:p。
- slice(X,Y,Z,V,nx,ny,nz):显示三元函数V(X,Y,Z)确定的立体图在x轴、y轴、z轴方向上的若干点(对应若干平面)的切片图。若函数V(X,Y,Z)中有一个变量X取定值X0,则函数V(X0,Y,Z)为X=X0立体面的切面图(将该切面通过颜色表示V的值),各点的坐标由数量向量sx、sy、sz指定。参量X、Y、Z均为三维数组,用于指定立方体V的每点的三维坐标。
- slice(V,XI,YI,ZI):显示由参量矩阵 XI、YI、ZI 确定的立体图的切片图,参量XI、YI、ZI定义了一个曲面,同时会在曲面的点上计算立体图V的值。需要注意的是,XI、YI、ZI必须为同型矩阵。
- slice(X,Y,Z,V,XI,YI,ZI):沿着由矩阵XI、YI、ZI定义的曲面穿过立体图V的切片图。
- slice(...,'method'):通过method来指定内插值的方法,method可取linear、cubic、nearest。linear指定的内插值方法为三次线性内插值(若未指定,此即为默认值),cubic指定使用三次立方内插值法,nearest指定使用最近点内插值法。
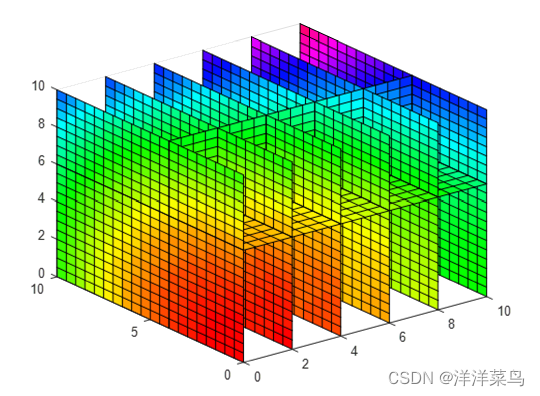
例8:slice函数示例
clear;
clc;
[x,y,z] = meshgrid(0:.5:10,0:.5:10,0:.5:10);
c = x.^2+y.^2+z.^2;
xs = [0,2,4,6,8,10];
ys = [4];
zs = [6]; % xs,ys,zs可决定切片形式和位置,helpslice可明白其具体含义
slice(x,y,z,c,xs,ys,zs)
colormap hsv
运行结果:
相关文章:

18、多维图形绘制
目录 一、三维图形绘制 (一)曲线图绘制plot3() (二)网格图绘制 mesh() (三)曲面图绘制 surf() (四)光照模型 surfl() (五)等值线图(等高线图)绘制 cont…...
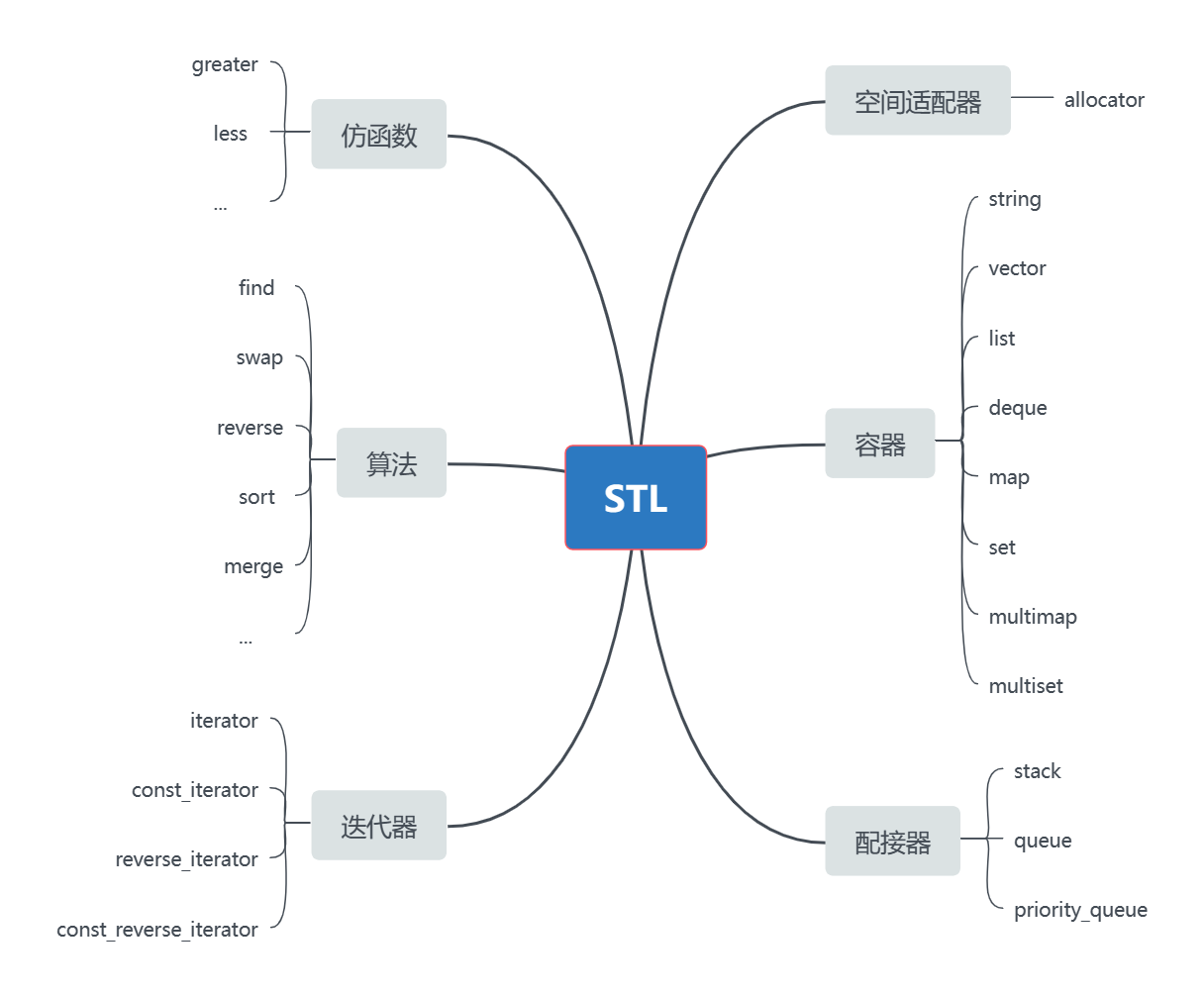
【C++】30h速成C++从入门到精通(STL介绍、string类)
STL简介什么是STLSTL(standard template libaray-标准模板库):是C标准库的重要组成部分,不仅是一个可复用的组件库,而且是一个包罗数据结构与算法的软件框架。STL的版本原始版本Alexander Stepanov、Meng Lee 在惠普实验室完成的原始版本&…...

PMP是什么意思?适合哪些人学呢?
PMP简而言之,就是提高项目管理理论基础和实践能力的考试。 官方一点的说明呢,就是:PMP证书全称为Project Management Professional,也叫项目管理专业人士资格认证。 PMP证书由美国项目管理协会(PMI)发起,是严格评估项…...

【SpringBoot 事务不回滚?怎么解决?】
SpringBoot 事务不回滚可能有多种原因,下面列举一些常见的原因和对应的解决方法: 异常被捕获处理了 如果方法中抛出了异常,但是在方法中被捕获并处理了,那么事务不会回滚。解决方法是让异常继续抛出,或者使用 Transa…...

软件研发管理经验总结 - 技术管理
软件研发管理经验总结 - 技术管理 技术管理主要负责有技术团队建设、管理团队成员技术相关事务、帮助团队成员成长、负责团队成员交付的代码质量、以及负责产品技术方向、以及产品相关前沿技术调研;管理团队成员技术相关事务有代码Review、故障率跟踪、分析及根据分…...

项目实战典型案例19——临时解决方案和最终解决方案
临时解决方案和最终解决方案一:背景介绍二:思路&方案四:总结五:升华一:背景介绍 本篇博客是对项目开发中出现的临时解决方案和最终解决方案进行的总结和改进。目的是将经历转变为自己的经验。通过博客的方式分享给…...

机器学习模型的可解释性算法汇总!
模型可解释性汇总简 介目前很多机器学习模型可以做出非常好的预测,但是它们并不能很好地解释他们是如何进行预测的,很多数据科学家都很难知晓为什么该算法会得到这样的预测结果。这是非常致命的,因为如果我们无法知道某个算法是如何进行预测&…...

什么是着色器/Threejs如何使用着色器/Threejs使用着色器实现平面网格的动态效果案例
1,什么是着色器着色器(Shader)是计算机图形学中的一个重要概念,它是在 GPU 上运行的程序,用于计算三维场景中每个像素的颜色和其他属性。着色器通常分为两种类型:顶点着色器和片元着色器。顶点着色器主要用…...
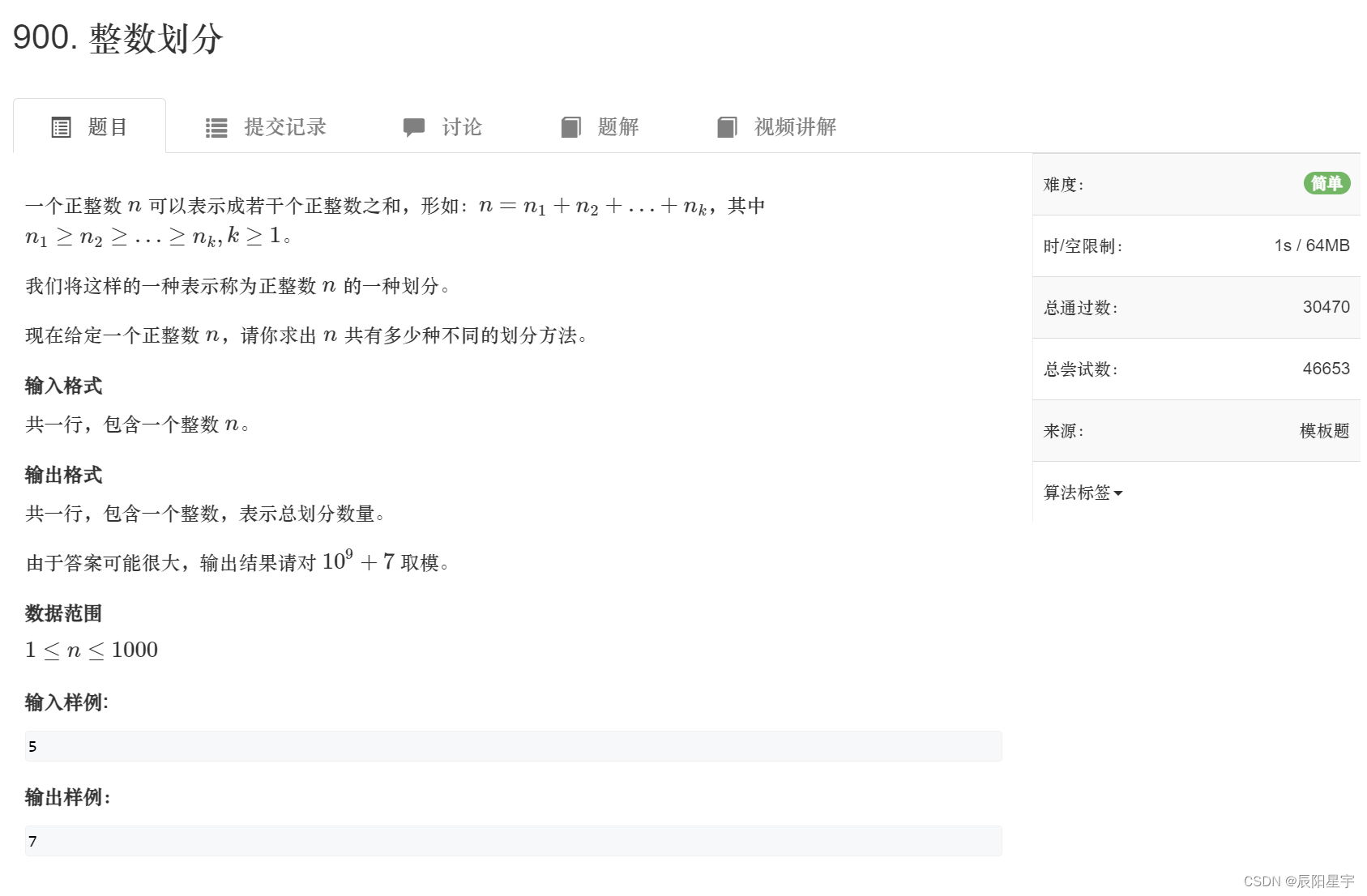
191、【动态规划】AcWing ——AcWing 900. 整数划分:完全背包解法+加减1解法(C++版本)
题目描述 参考文章:900. 整数划分 解题思路 因为本题中规定了数字从大到小,其实也就是不论是1 2 1 4,还是2 1 1 4,都会被看作是2 1 1 4这一种情况,因此本题是在遍历中不考虑结果顺序。 背包问题中只需考虑…...

Java 比较器
public interface Comparable Comparable 接口位于 java.lang 包下,对实现它的每个类的对象强加一个总排序,这种排序被称为类的自然顺序,compareTo 方法被称为其自然比较方法。 实现此接口的对象的列表(和数组)可以由…...

配置本地 python GEE、geemap环境
1.安装anconda 百度搜索anconda清华镜像,从清华镜像中选择最新的anconda安装包,国内镜像网站下载速度较快,如果从国外官网下载速度相当慢,详细安装教程请参考: anconda安装教程https://blog.csdn.net/lwbCUMT/article…...
cmd命令教程
小提示: 在本文中,我将向您展示可以在 Windows 命令行上使用的 40 个命令 温馨提示:在本教程中学习使用适用于 Windows 10 和 CMD 网络命令的最常见基本 CMD 命令及其语法和示例 文章目录为什么命令提示符有用一、cmd是什么?如何在…...

深圳大学计软《面向对象的程序设计》实验15 函数模板和类模板
A. 有界数组模板类(类模板) 题目描述 编写有界数组模板BoundArray(即检查对数组元素下标引用并在下标越界时终止程序的执行),能够存储各种类型的数据。要求实现对数组进行排序的方法sort,及对数组进行查找…...
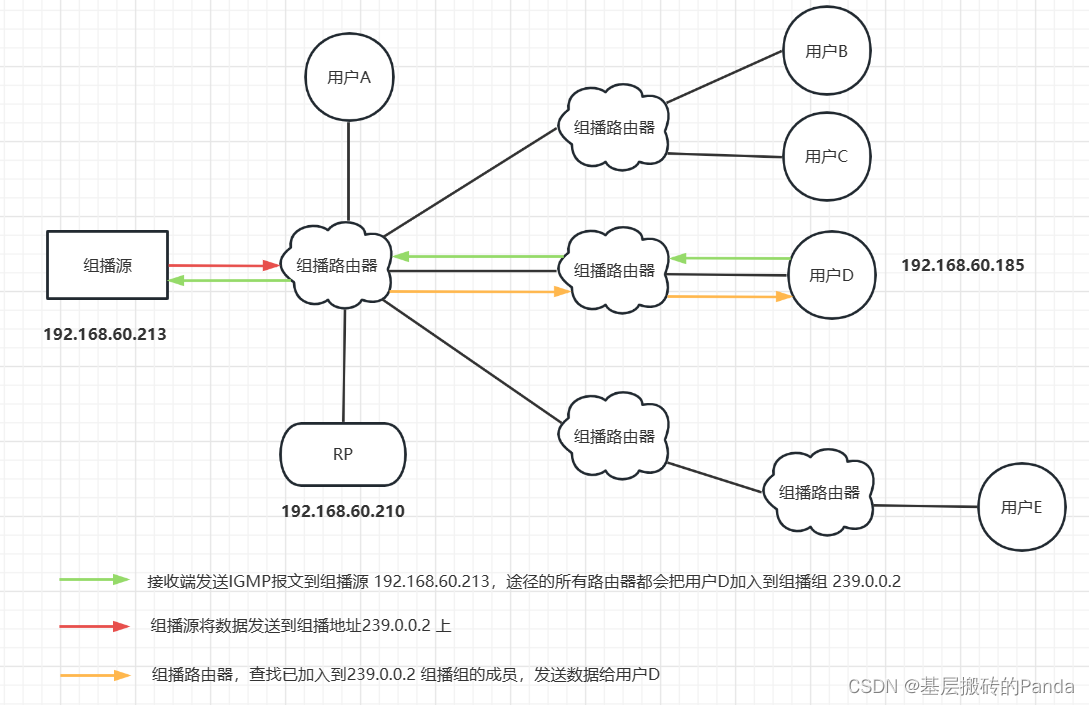
组播详解及示例代码
写在前面 由于公司业务需要用到组播实现,这里就记录下学习过程。在学习组播之前,我们先来看看另外两种数据包传输方式:单播和广播。 单播:简单来说就是数据一对一发送,如果需要给多个主机发送数据时,就需…...
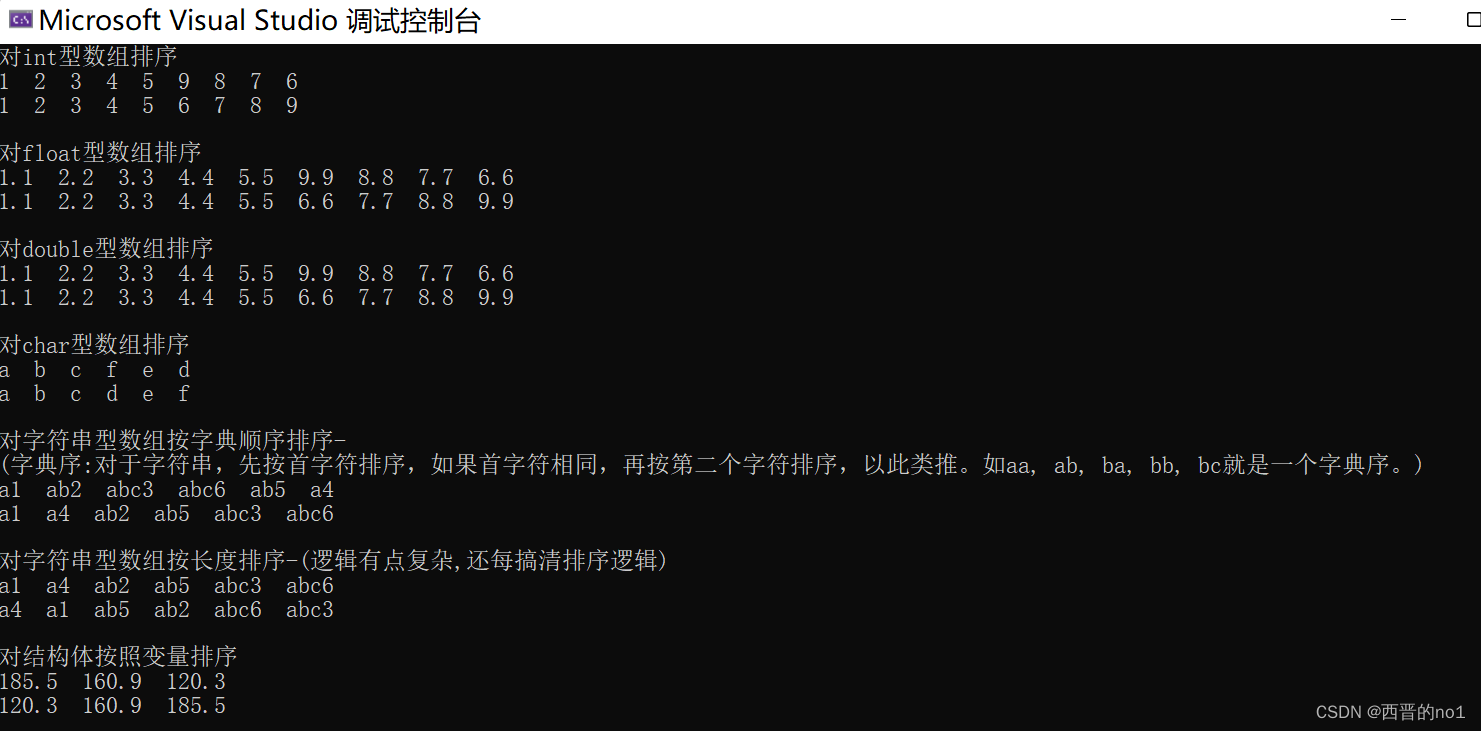
C语言-qsort函数示例解析
一.qsort函数是什么stdlib.h头文件下的函数qsort()函数:是八大排序算法中的快速排序,能够排序任意数据类型的数组其中包括整形,浮点型,字符串甚至还有自定义的结构体类型。qsort函数实现对不同元素的排序主要就是通过对compar函数…...

一些Linux内核内存性能调优笔记!
前言 在工作生活中,我们时常会遇到一些性能问题:比如手机用久了,在滑动窗口或点击 APP 时会出现页面反应慢、卡顿等情况;比如运行在某台服务器上进程的某些性能指标(影响用户体验的 PCT99 指标等)不达预期…...

【JVM】逃逸分析
开发者都知道,基本上所有对象都是在堆上创建。但是,这里还是没有把话说绝对哈,指的是基本上所有。昨天一位朋友在聊天中,就说了所有对象都在堆中创建,然后被朋友一阵的嘲笑。 开始我们的正文,我们今天来聊聊…...

C51---震动传感器控制LED灯亮灭
1.example #include "reg52.h" sbit led1 P3^7;//原理图中led1指向P3组IO口的P3.7口 sbit vibrate P3^3;//Do接到了P3.3口 void Delay3000ms() //11.0592MHz { unsigned char i, j, k; //_nop_(); i 22; j 3; k 227; do { …...
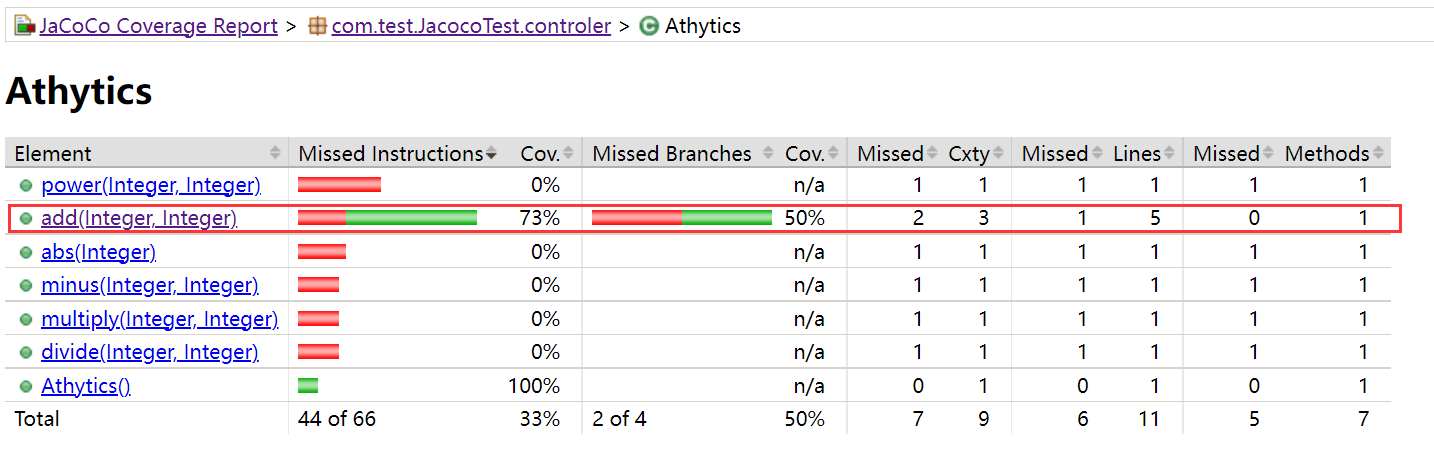
使用 JaCoCo 生成测试覆盖率报告
0、为什么要生成测试覆盖率报告 在我们实际的工作中,当完成程序的开发后,需要提交给测试人员进行测试,经过测试人员测试后,代码才能上线到生产环境。 有个问题是:怎么能证明程序得到了充分的测试,程序中所…...

windows下neo4j安装及配置,并绘制人物关系图谱
neo4j安装及配置,绘制人物关系图谱 先升级pip,安装py2neo pip install py2neo2021.0.1依赖 jdk1.8, neo4j 3.xx; 或者jdk18,neo4j 4.x,5.x; 官网下载了neo4j4.x,5.x 因为jdk版本原因都不行&am…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
