191、【动态规划】AcWing ——AcWing 900. 整数划分:完全背包解法+加减1解法(C++版本)
题目描述
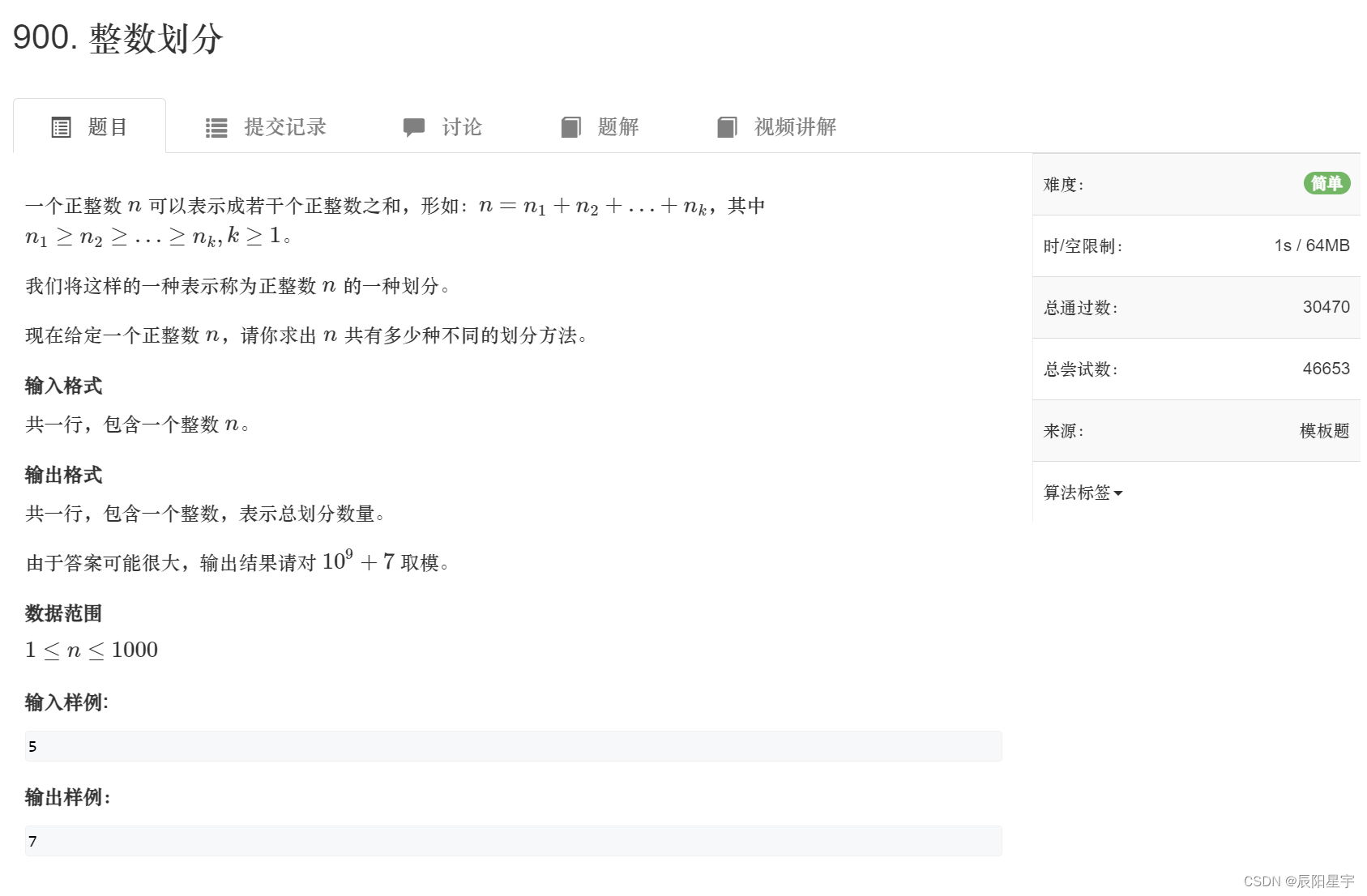
参考文章:900. 整数划分
解题思路
因为本题中规定了数字从大到小,其实也就是不论是1 + 2 + 1 = 4,还是2 + 1 + 1 = 4,都会被看作是2 + 1 + 1 = 4这一种情况,因此本题是在遍历中不考虑结果顺序。
背包问题中只需考虑使用的物品种类,因此可转化为完全背包问题,将组成的数看作物品且容量为1n,背包容量为n。本题便转化为了,从物品1物品n(体积也是为1~n)中进行选择,构成背包容量为n的方案个数。
(1)完全背包二维数组
- 动态规划五步曲:
(1)dp[i][j]含义: 从1~i中选择物品,达到背包容量为j的方案个数。
(2)递推公式: dp[i][j]=(dp[i−1][j]+dp[i][j−i])dp[i][j] = (dp[i - 1][j] + dp[i][j - i])dp[i][j]=(dp[i−1][j]+dp[i][j−i]),完全背包的一般性化简后递推公式,未化简前所表示的是尝试放入物品1到物品j后的情况。
(3)dp数组初始化: dp[i][0] = 1,容量为0时,仅有一种情况。
(4)遍历顺序: 从左到右,从上到下。
(5)举例: (省略)
#include <iostream>using namespace std;const int N = 1010, mod = 1e9 + 7;
int n;
int dp[N][N];int main() {cin >> n;for(int i = 1; i <= n; i++) dp[i][0] = 1;for(int i = 1; i <= n; i++) {for(int j = 1; j <= n; j++) {if(i > j) dp[i][j] = dp[i - 1][j] % mod;else dp[i][j] = (dp[i - 1][j] + dp[i][j - i]) % mod;}}cout << dp[n][n] << endl;return 0;
}(2)完全背包一维滚动数组
对变量进行优化
#include <iostream>using namespace std;const int N = 1010, mod = 1e9 + 7;
int n;
int dp[N];int main() {cin >> n;dp[0] = 1;for(int i = 1; i <= n; i++) {for(int j = i; j <= n; j++) {dp[j] = (dp[j] + dp[j - i]) % mod;}}cout << dp[n] << endl;return 0;
}(3)用加减1方法
此方法主要使用的是加一个和减一个1,还保持某种方案不变化的特点,得来递推公式。因为我们要求的只是方案个数,
例如:组合成3的方案可以为2、1和1、1、1,当我们想要得到组合成4的方案,那么就可以分别从2、1和1、1、1演化过来,就是2、1、1和1、1、1、1,此时3中这一部分含有最小值为1的方案个数与4中这一部分含有最小值为1的方案个数其实是相同的。
(1)dp[i][j]含义: 由j个数组合成总和为i的方案个数
(2)递推公式: dp[i][j]=dp[i−1][j−1]+dp[i−j][j]dp[i][j] = dp[i - 1][j - 1] + dp[i - j][j]dp[i][j]=dp[i−1][j−1]+dp[i−j][j],将状态集合划分成两部分,一部分是j个数中的最小值值是1,另一部分是j个数中的最小值大于1。
对于最小值是1的集合,状态转移为dp[i][j]=dp[i−1][j−1]dp[i][j] = dp[i - 1][j - 1]dp[i][j]=dp[i−1][j−1],意思为当前状态由少一个1的状态演变过来。因为我们要求的是组合成目标数是的方案个数,因此加上一个时,其实还是在此种方案下,故方案个数与dp[i - 1][j - 1]的方案个数相同。
对于最大值大于1的集合,状态转移为dp[i][j]=dp[i−j][j]dp[i][j] = dp[i - j][j]dp[i][j]=dp[i−j][j],还是利用1这种特点,将j个数中各自减去一个1,此时dp[i][j]就可以有dp[i - j][j]而来。
(3)dp数组初始化: dp[0][0] = dp[1][1] = 1,重量为0和1时仅有一种方案。
(4)遍历顺序: 从左到右,从上到下。
(5)举例:
例如:组合成3的方案可以为2、1和1、1、1,当我们想要得到组合成4的方案,那么就可以分别从2、1和1、1、1演化过来,就是2、1、1和1、1、1、1,此时3中这一部分含有最小值为1的方案个数与4中这一部分含有最小值为1的方案个数其实是相同的。
#include <iostream>using namespace std;const int N = 1010, mod = 1e9 + 7;
int n;
int dp[N][N];int main() {cin >> n;dp[0][0] = dp[1][1] = 1;for(int i = 1; i <= n; i++) {for(int j = 1; j <= i; j++) {dp[i][j] = (dp[i - 1][j - 1] + dp[i - j][j]) % mod;}}int res = 0;for(int i = 1; i <= n; i++) res = (dp[n][i] + res) % mod;cout << res << endl;return 0;
}
相关文章:

191、【动态规划】AcWing ——AcWing 900. 整数划分:完全背包解法+加减1解法(C++版本)
题目描述 参考文章:900. 整数划分 解题思路 因为本题中规定了数字从大到小,其实也就是不论是1 2 1 4,还是2 1 1 4,都会被看作是2 1 1 4这一种情况,因此本题是在遍历中不考虑结果顺序。 背包问题中只需考虑…...

Java 比较器
public interface Comparable Comparable 接口位于 java.lang 包下,对实现它的每个类的对象强加一个总排序,这种排序被称为类的自然顺序,compareTo 方法被称为其自然比较方法。 实现此接口的对象的列表(和数组)可以由…...

配置本地 python GEE、geemap环境
1.安装anconda 百度搜索anconda清华镜像,从清华镜像中选择最新的anconda安装包,国内镜像网站下载速度较快,如果从国外官网下载速度相当慢,详细安装教程请参考: anconda安装教程https://blog.csdn.net/lwbCUMT/article…...
cmd命令教程
小提示: 在本文中,我将向您展示可以在 Windows 命令行上使用的 40 个命令 温馨提示:在本教程中学习使用适用于 Windows 10 和 CMD 网络命令的最常见基本 CMD 命令及其语法和示例 文章目录为什么命令提示符有用一、cmd是什么?如何在…...

深圳大学计软《面向对象的程序设计》实验15 函数模板和类模板
A. 有界数组模板类(类模板) 题目描述 编写有界数组模板BoundArray(即检查对数组元素下标引用并在下标越界时终止程序的执行),能够存储各种类型的数据。要求实现对数组进行排序的方法sort,及对数组进行查找…...
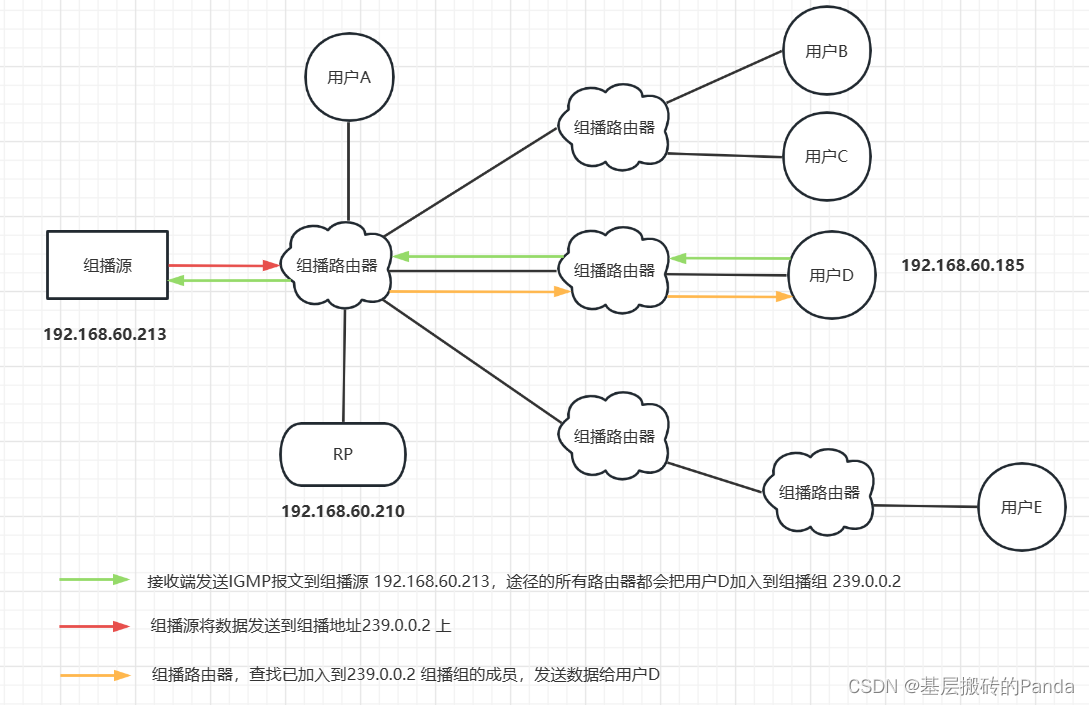
组播详解及示例代码
写在前面 由于公司业务需要用到组播实现,这里就记录下学习过程。在学习组播之前,我们先来看看另外两种数据包传输方式:单播和广播。 单播:简单来说就是数据一对一发送,如果需要给多个主机发送数据时,就需…...
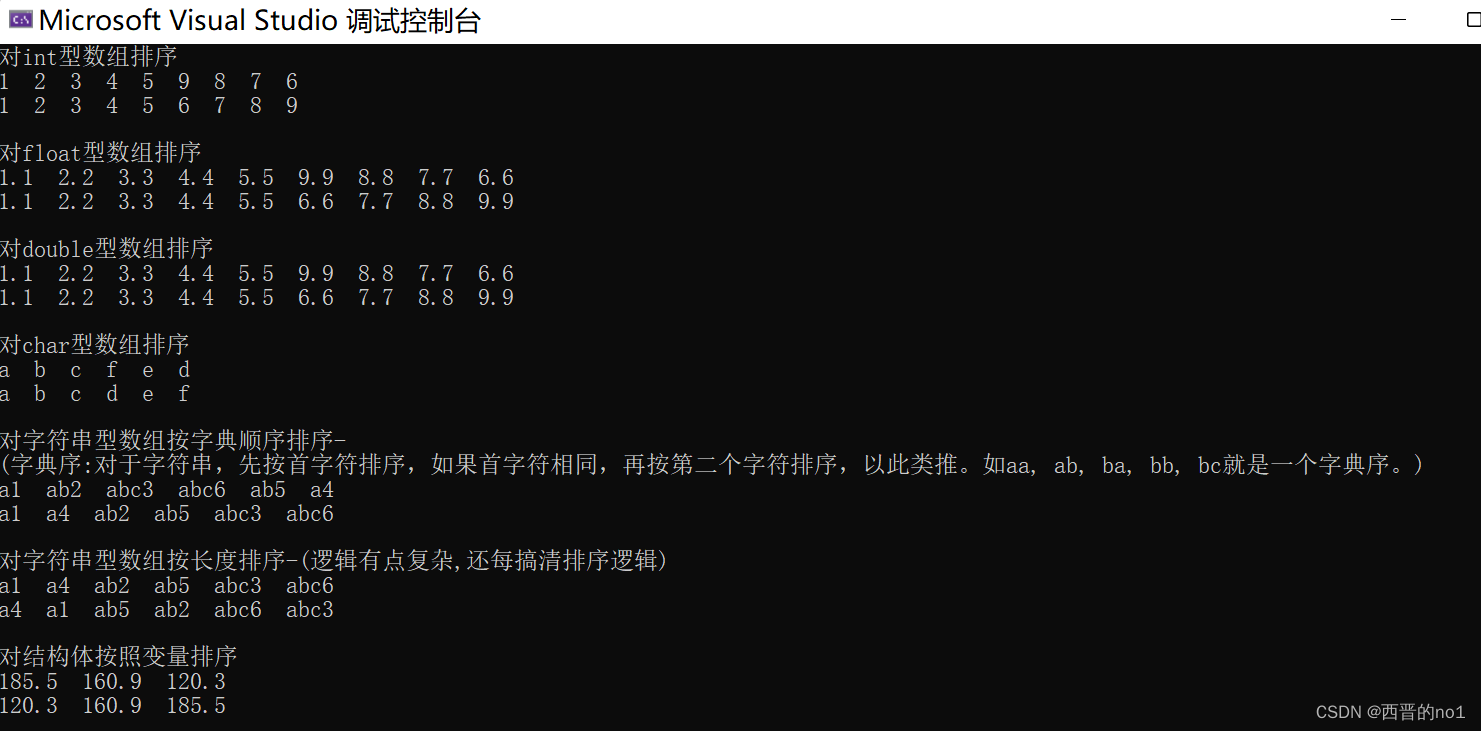
C语言-qsort函数示例解析
一.qsort函数是什么stdlib.h头文件下的函数qsort()函数:是八大排序算法中的快速排序,能够排序任意数据类型的数组其中包括整形,浮点型,字符串甚至还有自定义的结构体类型。qsort函数实现对不同元素的排序主要就是通过对compar函数…...

一些Linux内核内存性能调优笔记!
前言 在工作生活中,我们时常会遇到一些性能问题:比如手机用久了,在滑动窗口或点击 APP 时会出现页面反应慢、卡顿等情况;比如运行在某台服务器上进程的某些性能指标(影响用户体验的 PCT99 指标等)不达预期…...

【JVM】逃逸分析
开发者都知道,基本上所有对象都是在堆上创建。但是,这里还是没有把话说绝对哈,指的是基本上所有。昨天一位朋友在聊天中,就说了所有对象都在堆中创建,然后被朋友一阵的嘲笑。 开始我们的正文,我们今天来聊聊…...

C51---震动传感器控制LED灯亮灭
1.example #include "reg52.h" sbit led1 P3^7;//原理图中led1指向P3组IO口的P3.7口 sbit vibrate P3^3;//Do接到了P3.3口 void Delay3000ms() //11.0592MHz { unsigned char i, j, k; //_nop_(); i 22; j 3; k 227; do { …...
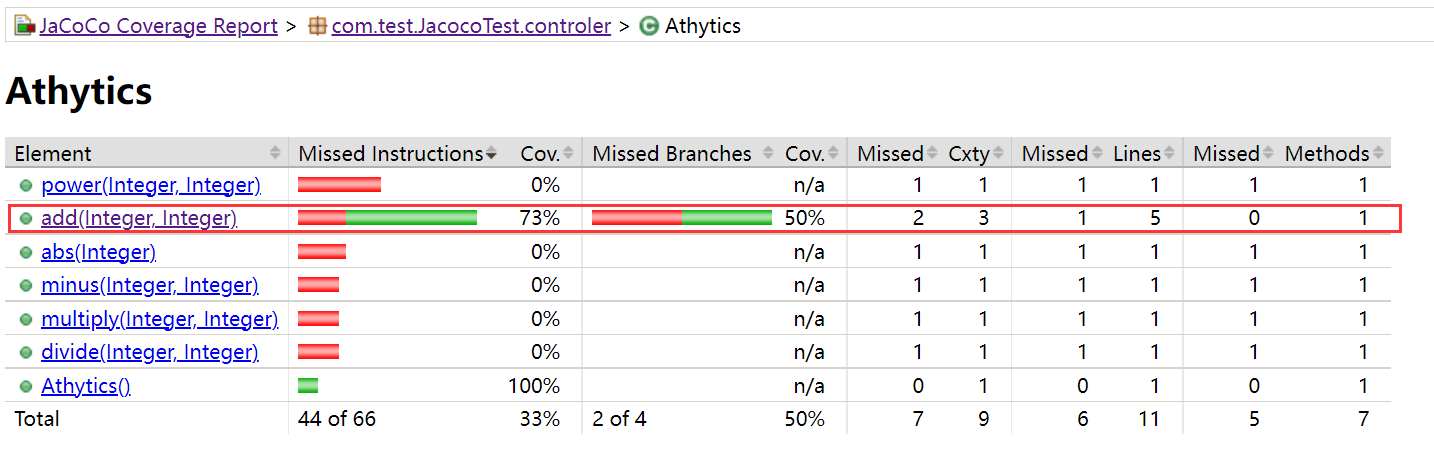
使用 JaCoCo 生成测试覆盖率报告
0、为什么要生成测试覆盖率报告 在我们实际的工作中,当完成程序的开发后,需要提交给测试人员进行测试,经过测试人员测试后,代码才能上线到生产环境。 有个问题是:怎么能证明程序得到了充分的测试,程序中所…...

windows下neo4j安装及配置,并绘制人物关系图谱
neo4j安装及配置,绘制人物关系图谱 先升级pip,安装py2neo pip install py2neo2021.0.1依赖 jdk1.8, neo4j 3.xx; 或者jdk18,neo4j 4.x,5.x; 官网下载了neo4j4.x,5.x 因为jdk版本原因都不行&am…...
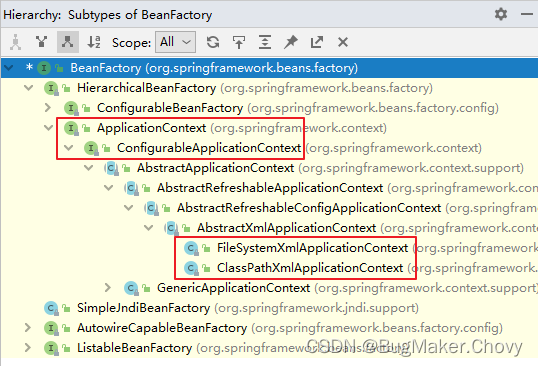
【Spring6】IoC容器之基于XML管理Bean
3、容器:IoC IoC 是 Inversion of Control 的简写,译为“控制反转”,它不是一门技术,而是一种设计思想,是一个重要的面向对象编程法则,能够指导我们如何设计出松耦合、更优良的程序。 Spring 通过 IoC 容…...

Warshall算法求传递闭包及Python编程的实现
弗洛伊德算法-Floyd(Floyd-Warshall)-求多源最短路径,求传递闭包 Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法, 与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大…...

AcWing第 93 场周赛
4867. 整除数 给定两个整数 n,k,请你找到大于 n 且能被 k 整除的最小整数 x。 输入格式 共一行,包含两个整数 n,k。 输出格式 输出大于 n 且能被 k 整除的最小整数 x。 数据范围 前 4 个测试点满足 1≤n,k≤100。 所有测试点满足 1≤n,k≤109。 …...

计及需求响应的粒子群算法求解风能、光伏、柴油机、储能容量优化配置(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
利用Nginx给RStudio-Server配置https
前篇文档,我这边写了安装RStudio-Server的方法。默认是http的访问方式,现在我们需要将其改成https的访问方式。 1、给服务器安装Nginx:参照之前的安装Nginx的方法。 2、创建/usr/local/nginx/ssl目录: mkdir /usr/local/nginx/ss…...

YOLOv7实验记录
这篇博客主要记录博主在做YOLOv7模型训练与测试过程中遇到的一些问题。 首先我们需要明确YOLO模型权重文件与模型文件的使用 其实在github的readme中已经告诉我们使用方法,但我相信有很多像博主一样眼高手低的人可能会犯类似的错误。 训练 首先是训练时的设置&…...

用Python获取史瓦西时空中克氏符的分量
文章目录三维球面坐标史瓦西时空三维球面坐标 Einsteinpy中提供了克氏符模型,可通过ChristoffelSymbols获取。简单起见,先以最直观的三维球面为例,来用Einsteinpy查看其克氏符的表达形式。 三维球面的度规张量可表示为 g001g11r2g22r2sin…...
QML编码约定
QML中的国际化: QML使用以下函数来将字符串标记为可翻译的 qsTr()qsTranslate()qsTrld()QT_TR_NOOP()QT_TRANSLATE_NOOP()QT_TRID_NOOP最常用的还是qsTr() string qsTr(string sourceText, string disambiguation&…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
