AcWing第 93 场周赛
4867. 整除数
给定两个整数 n,k,请你找到大于 n 且能被 k 整除的最小整数 x。
输入格式
共一行,包含两个整数 n,k。
输出格式
输出大于 n 且能被 k 整除的最小整数 x。
数据范围
前 4 个测试点满足 1≤n,k≤100。
所有测试点满足 1≤n,k≤109。
输入样例1:
5 3
输出样例1:
6
输入样例2:
25 13
输出样例2:
26
输入样例3:
26 13
输出样例3:
39#include<bits/stdc++.h>
using namespace std;
int main(){long long n,k;cin>>n>>k;cout<<(n/k+1)*k;return 0;
}4868. 数字替换
给定两个整数 n,x。
你可以对 x 进行任意次以下操作:
- 选择 x� 的一位数字 y�,将 x� 替换为 x×y�×�。
请你计算通过使用上述操作,将 x� 变为一个 n� 位数字(不含前导 00),所需要的最少操作次数。
例如,当 n=3,x=2�=3,�=2 时,对 22 进行如下 44 次操作,即可使其变为 33 位数字:
- 将 22 替换为 2×2=42×2=4。
- 将 44 替换为 4×4=164×4=16。
- 将 1616 替换为 16×6=9616×6=96。
- 将 9696 替换为 96×9=86496×9=864。
输入格式
共一行,包含两个整数 n,x�,�。
输出格式
一个整数,表示将 x� 变为一个 n� 位数字,所需要的最少操作次数。
如果无解,则输出 -1。
数据范围
所有测试点满足 2≤n≤192≤�≤19,1≤x<10n−11≤�<10�−1。
输入样例1:
2 1
输出样例1:
-1
输入样例2:
3 2
输出样例2:
4
输入样例3:
13 42
输出样例3:
12#include <bits/stdc++.h>
using namespace std;int n, ans = 2e9;
long long x, st;
map<long long, int> used;int bfs()
{unordered_map<unsigned long long, int> s;queue<long long> q;q.push(x);while (q.size()){long long t = q.front();q.pop();for (long long p = t; p; p /= 10){if (p % 10 == 0 || p % 10 == 1) continue;unsigned long long k = p % 10 * t;if (s[p % 10 * t]) continue;q.push(k), s[k] = s[t] + 1;if (k >= st) return s[k];}}return -1;
}int main()
{scanf("%d%lld", &n, &x);st = pow(10, n - 1);printf("%d", bfs());return 0;
} 4869. 异或值
给定一个长度为 n� 的整数序列 a1,a2,…,an�1,�2,…,��。
请你找到一个非负整数 X�,使得 max1≤i≤n{ai⊕X}max1≤�≤�{��⊕�} 的值尽可能小,其中 ⊕⊕ 表示按位异或。
输出 max1≤i≤n{ai⊕X} 的最小可能值。
输入格式
第一行包含整数 n。
第二行包含 n 个整数 a1,a2,…,an。
输出格式
一个整数,表示 max1≤i≤n{ai⊕X} 的最小可能值。
数据范围
前 33 个测试点满足 1≤n≤3。
所有测试点满足 1≤n≤105,0≤ai≤230−1。
输入样例1:
3
1 2 3
输出样例1:
2
输入样例2:
2
1 5
输出样例2:
4
#include <iostream>
using namespace std;
const int N = 100010,M = 31 * N;
int n;
int a[N];
int tr[M][2],cnt[M],idx;
void insert (int x) {int u = 0;for (int i = 30;i >= 0;i--) {int t = x >> i & 1;if (!tr[u][t]) tr[u][t] = ++idx;u = tr[u][t];}cnt[u]++;
}
int query (int u,int k) {if (tr[u][0] && tr[u][1]) return (1 << k) + min (query (tr[u][0],k - 1),query (tr[u][1],k - 1));if (tr[u][0]) return query (tr[u][0],k - 1);if (tr[u][1]) return query (tr[u][1],k - 1);return 0;
}
int main () {cin >> n;for (int i = 1;i <= n;i++) {cin >> a[i];insert (a[i]);}cout << query (0,30) << endl;return 0;
}
相关文章:

AcWing第 93 场周赛
4867. 整除数 给定两个整数 n,k,请你找到大于 n 且能被 k 整除的最小整数 x。 输入格式 共一行,包含两个整数 n,k。 输出格式 输出大于 n 且能被 k 整除的最小整数 x。 数据范围 前 4 个测试点满足 1≤n,k≤100。 所有测试点满足 1≤n,k≤109。 …...

计及需求响应的粒子群算法求解风能、光伏、柴油机、储能容量优化配置(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
利用Nginx给RStudio-Server配置https
前篇文档,我这边写了安装RStudio-Server的方法。默认是http的访问方式,现在我们需要将其改成https的访问方式。 1、给服务器安装Nginx:参照之前的安装Nginx的方法。 2、创建/usr/local/nginx/ssl目录: mkdir /usr/local/nginx/ss…...

YOLOv7实验记录
这篇博客主要记录博主在做YOLOv7模型训练与测试过程中遇到的一些问题。 首先我们需要明确YOLO模型权重文件与模型文件的使用 其实在github的readme中已经告诉我们使用方法,但我相信有很多像博主一样眼高手低的人可能会犯类似的错误。 训练 首先是训练时的设置&…...

用Python获取史瓦西时空中克氏符的分量
文章目录三维球面坐标史瓦西时空三维球面坐标 Einsteinpy中提供了克氏符模型,可通过ChristoffelSymbols获取。简单起见,先以最直观的三维球面为例,来用Einsteinpy查看其克氏符的表达形式。 三维球面的度规张量可表示为 g001g11r2g22r2sin…...
QML编码约定
QML中的国际化: QML使用以下函数来将字符串标记为可翻译的 qsTr()qsTranslate()qsTrld()QT_TR_NOOP()QT_TRANSLATE_NOOP()QT_TRID_NOOP最常用的还是qsTr() string qsTr(string sourceText, string disambiguation&…...
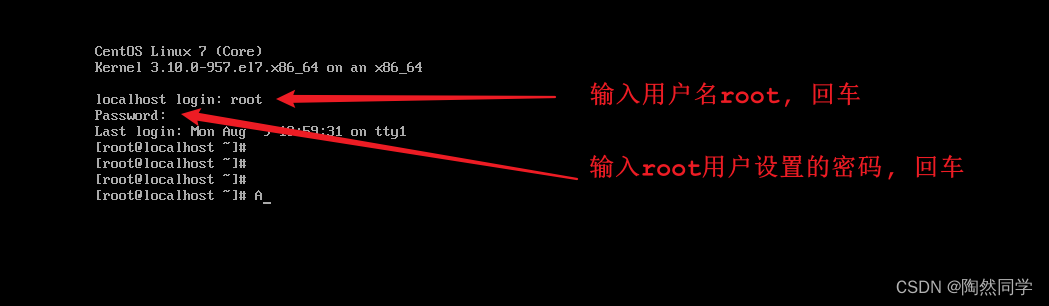
【Linux】安装Linux操作系统具体步骤
1). 选择创建新的虚拟机 2). 选择"典型"配置 3). 选择"稍后安装操作系统(S)" 4). 选择"Linux"操作系统,"CentOS7 64位"版本 5). 设置虚拟机的名称及系统文件存放路径 6). 设置磁盘容量 7). 自定义硬件信息 8). 启动上述创建的新虚拟机…...
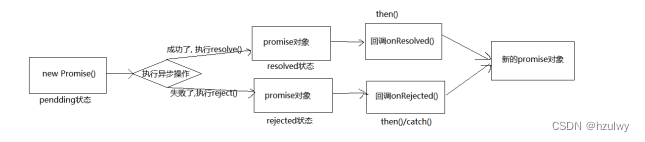
前端ES6异步编程技术——Promise使用
Promise是什么 官方的定义是:Promise是ES6新推出的用于进行异步编程的解决方案,旧方案是单纯使用回调函数来解决的。对于开发人员来说,我们把promise当作一个普通的对象即可,使用它可以用来封装一个异步操作并可以获取其成功/失败…...
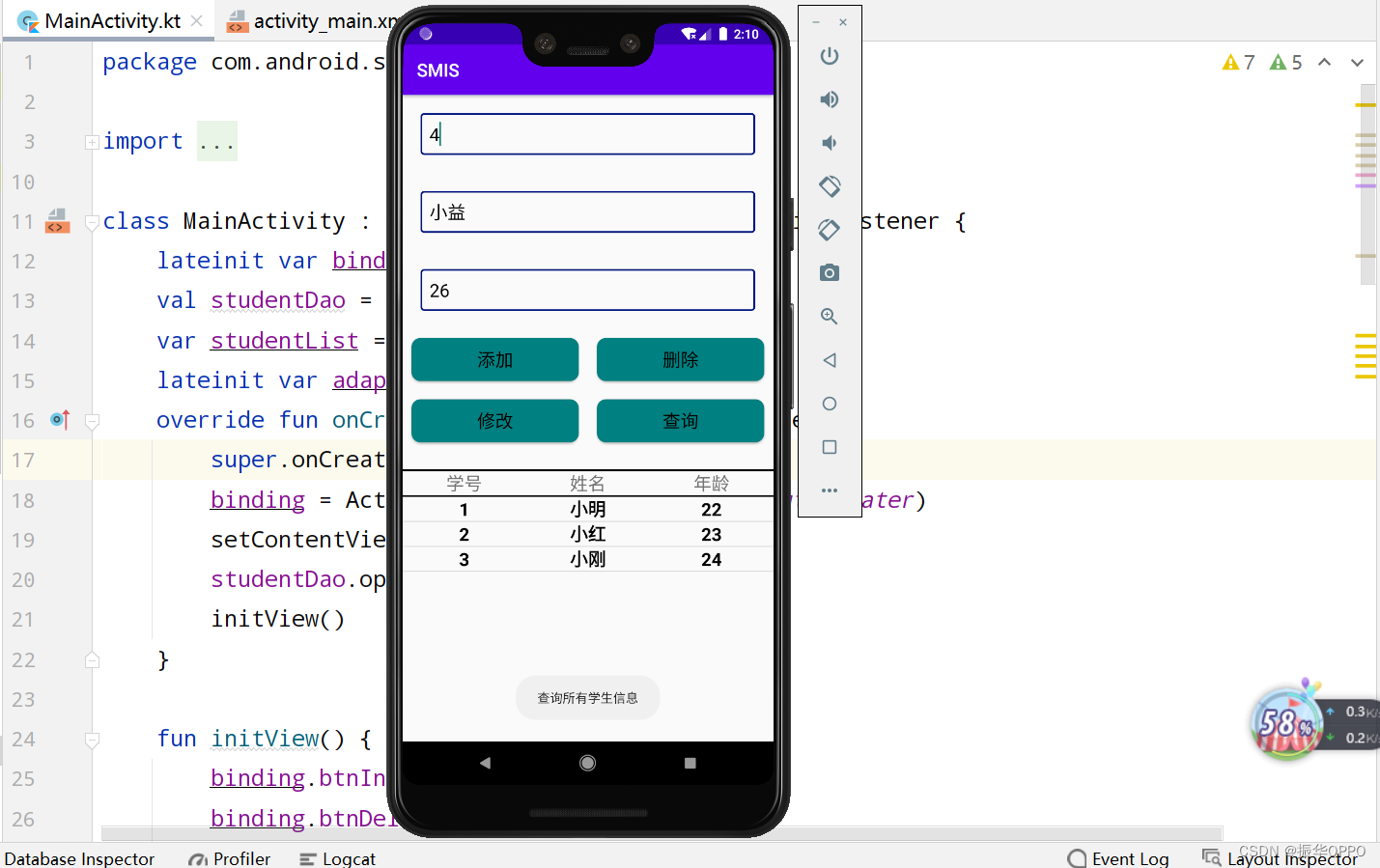
Kotlin实现简单的学生信息管理系统
文章目录一、实验内容二、实验步骤1、页面布局2、数据库3、登录活动4、增删改查三、运行演示四、实验总结五、源码下载一、实验内容 根据Android数据存储的内容,综合应用SharedPreferences和SQLite数据库实现一个用户信息管理系统,强化对SharedPreferen…...

413. 等差数列划分
413. 等差数列划分 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 nums ,返回数组 nums 中所有为等差数…...
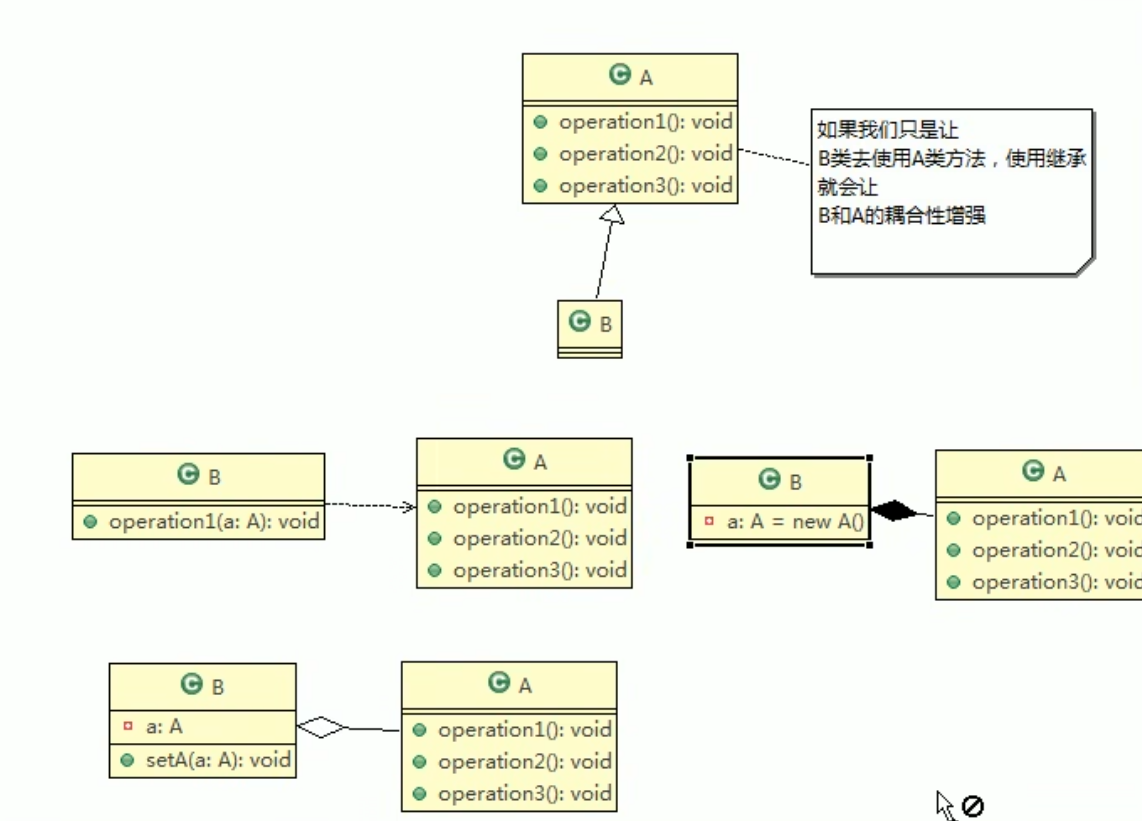
设计模式七大原则
一、设计模式概念 1.1 软件设计模式的产生背景 "设计模式"最初并不是出现在软件设计中,而是被用于建筑领域的设计中。 1977年美国著名建筑大师、加利福尼亚大学伯克利分校环境结构中心主任克里斯托夫亚历山大(Christopher Alexander&#x…...

【Mybatis系列】Mybatis常见的分页方法以及源码理解
Mybatis-Plus的selectPage 引入依赖 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.1</version></dependency>添加分页插件 Configuration public class My…...
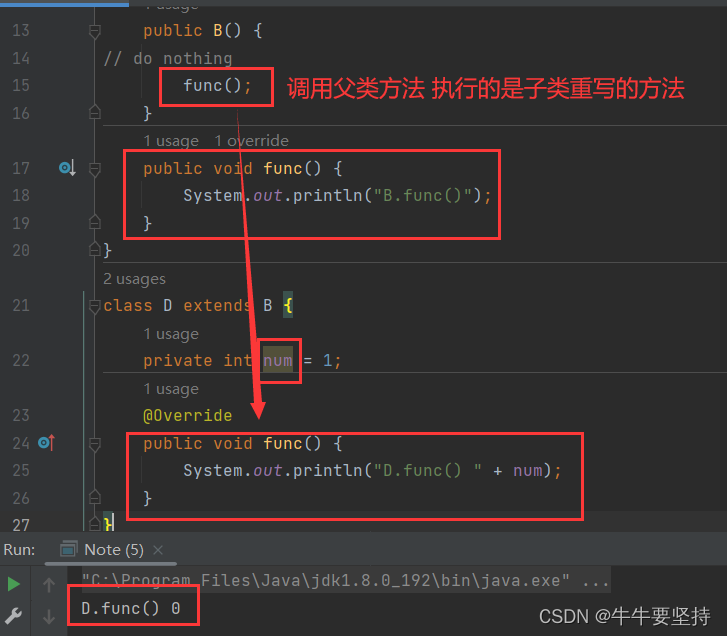
Java面向对象:多态特性的学习
本文介绍了Java面向对象多态特性, 多态的介绍. 多态的实现条件–1.发生继承.2.发生重写(重写与重载的区别)3.向上转型与向下转型.4.静态绑定和动态绑定5. 实现多态 举例总结多态的优缺点 避免在构造方法内调用被重写的方法… Java面向对象:多态特性的学习一.什么是多态?二.多态…...
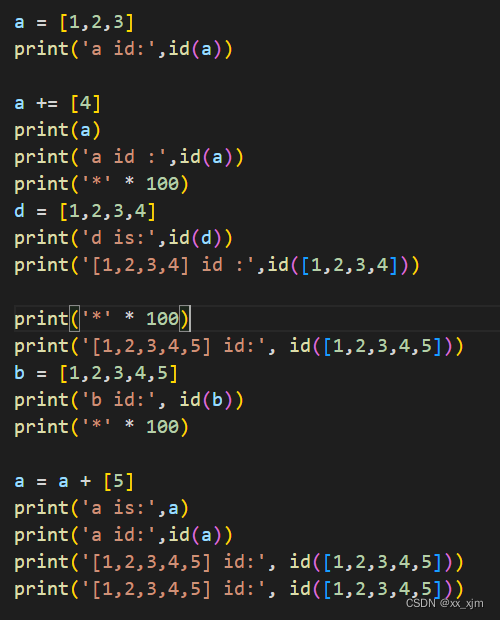
id函数 / 可变类型变量 / 不可变类型变量 / +=操作
前言 再说正文之前,需要大家先了解一下对象,指针和引用的含义,不懂得同学可以参考我上一篇博客“(12条消息) 引用是否有地址的讨论的_xx_xjm的博客-CSDN博客” 正文 一:python中一切皆对象 “python中一切皆对象”这句话我相信…...
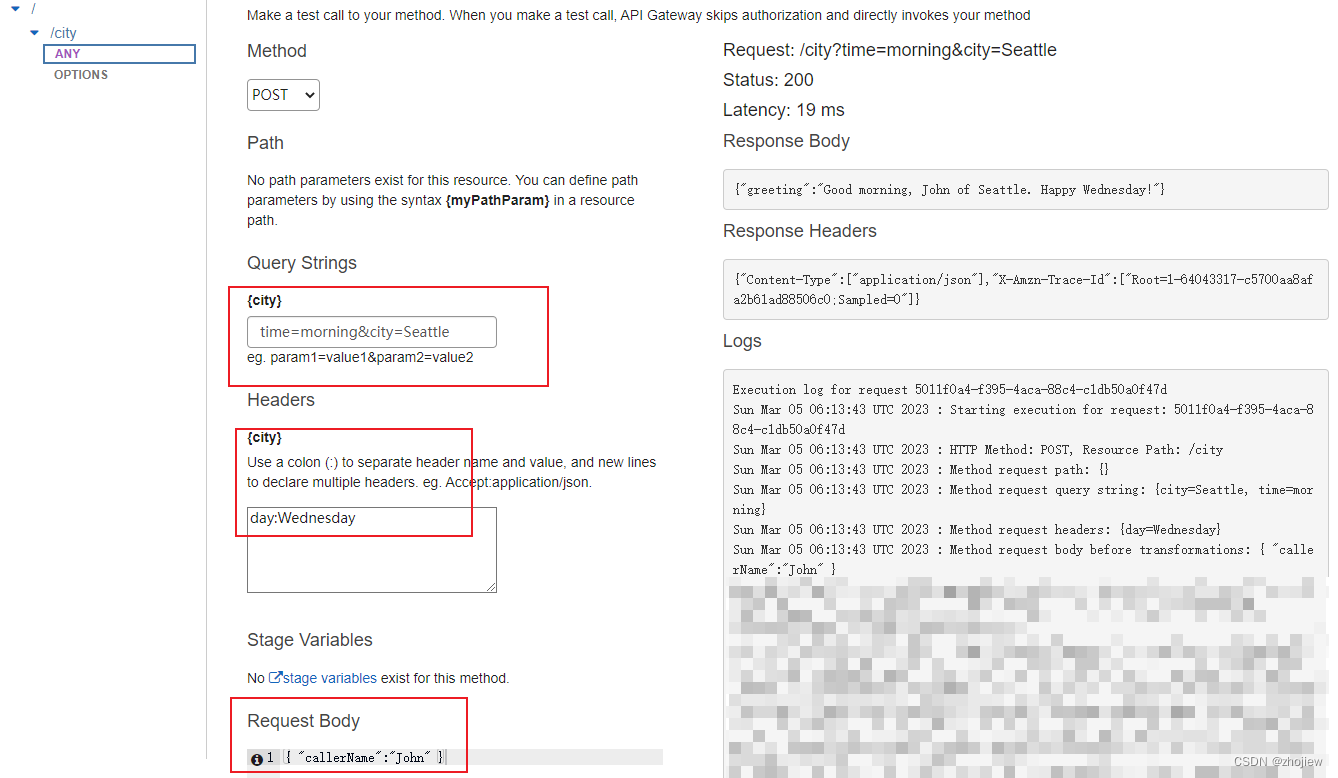
aws apigateway 使用apigateway集成lambda
参考资料 代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/api-gateway-create-api-as-simple-proxy-for-lambda.html非代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/getting-started-…...

Linux SPI 驱动实验
目录 一、Linux 下 SPI 驱动框架简介 1、SPI 主机驱动 2、SPI 设备驱动 SPI 设备数据收发处理流程 3、SPI 设备和驱动匹配过程 二、添加SPI 设备信息 1、添加 ICM20608 所使用的 IO 2、 在 ecspi3 节点追加 icm20608 子节点 三、编写 ICM20608 驱动 1、修改makefile…...
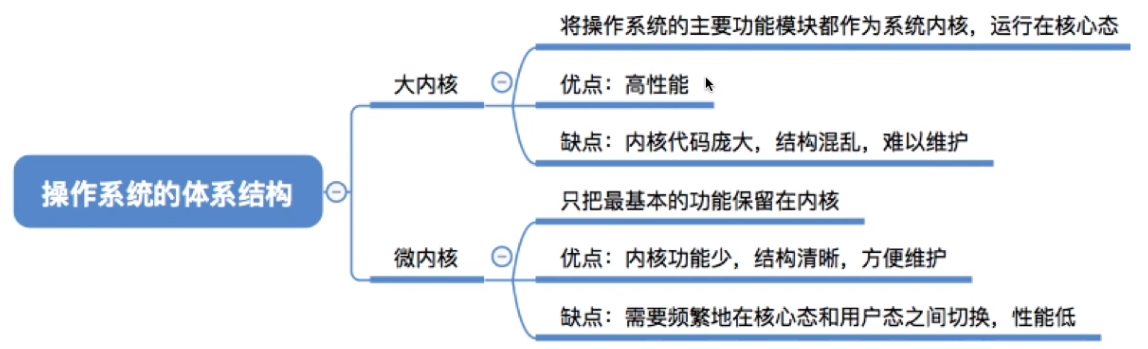
[1.4]计算机系统概述——操作系统的体系结构
第一章 计算机系统概述 操作系统的体系结构 大内核/单内核/宏内核微内核 通过之前的学习,我们知道计算机系统的层次结构是这样的。 但是操作系统的内部其实还可以再进一步地划分。 一部分是内核的功能,一部分是非内核的功能。 操作系统最核心的功能&…...
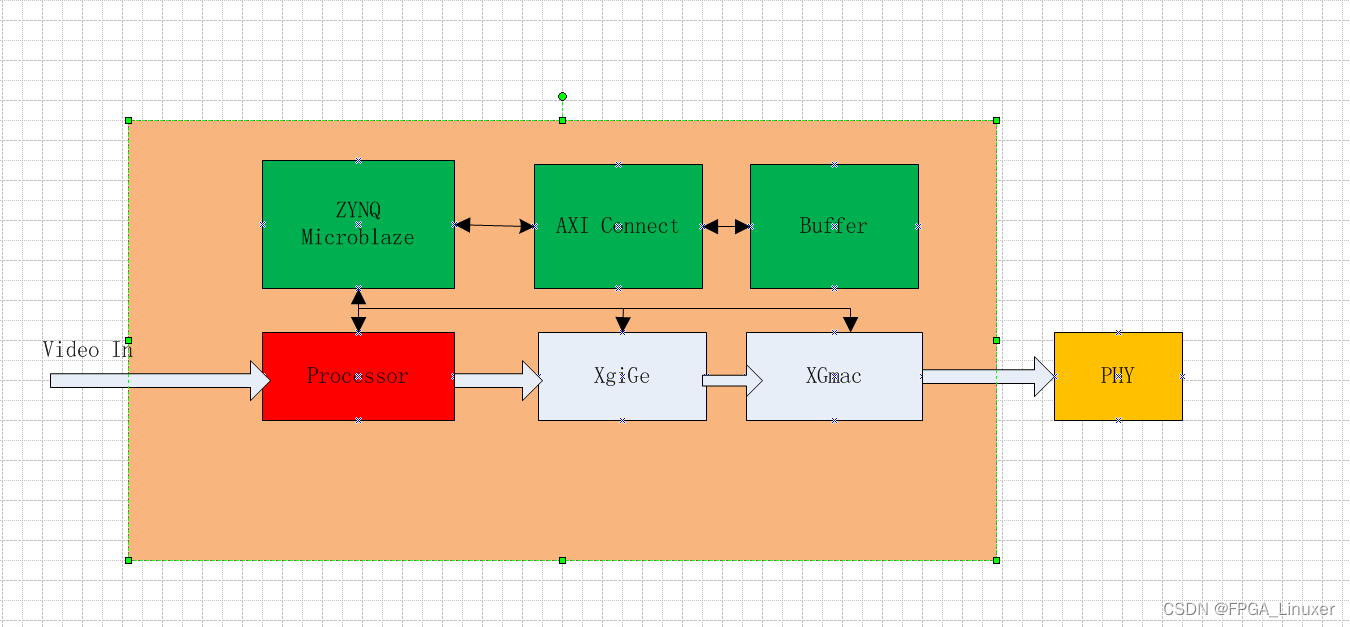
FPGA的GigE Vision IP相机图像采集方案设计,转换为千兆UDP,支持10G MAC
1 概述 GigE Vision是一个比较复杂的协议,要在FPGA中完全实现具有较大的难度。如果FPGA作为接收端希望实现GigE Vision相机的配置和图像采集功能,则只需要实现其中小部分功能即可。本文对原有GigE Vision协议的结构进行了裁剪,仅保留设备搜索…...
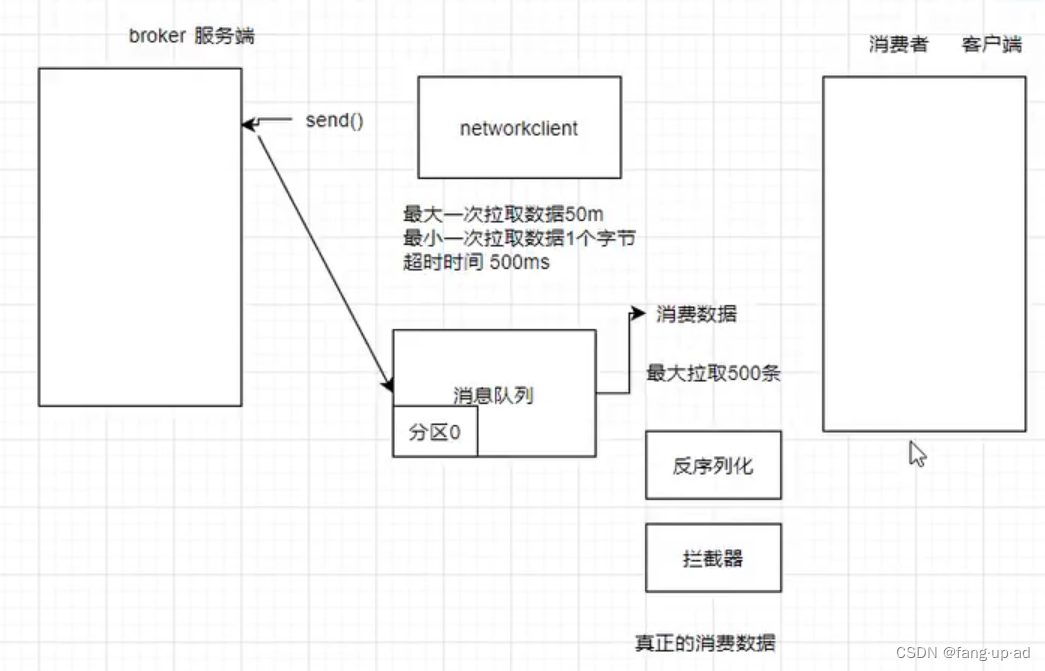
大数据相关面试题
linux 常见linux高级命令? top、iotopnetstatdf -hjmap -heaptarrpmps -efshell 用过的shell工具? awk Awk 命令详解 - 简书 awk是行处理器: 相比较屏幕处理的优点,在处理庞大文件时不会出现内存溢出或是处理缓慢的问题,通常用来…...

AI绘画第二步,抄作业复现超赞的效果!
上一篇,讲了如何安装AI绘画软件,但是装完后发现生成效果很渣!而网上那些效果都很赞。真的是理想很丰满,现实很骨感。今天就是来聊聊如何抄作业,最大程度的还原那些超赞的效果。换一种说法就是,教大家如何使…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
