用Python获取史瓦西时空中克氏符的分量
文章目录
- 三维球面坐标
- 史瓦西时空
三维球面坐标
Einsteinpy中提供了克氏符模型,可通过ChristoffelSymbols获取。简单起见,先以最直观的三维球面为例,来用Einsteinpy查看其克氏符的表达形式。
三维球面的度规张量可表示为
g00=1g11=r2g22=r2sin2θgij=0,i≠j\begin{aligned} g_{00}&=1\\ g_{11}&=r^2\\ g_{22}&=r^2\sin^2\theta\\ g_{ij}&=0, i\not=j \end{aligned} g00g11g22gij=1=r2=r2sin2θ=0,i=j
克氏符这个概念是从度规张量的协变导数为0的事实中得到的,换言之,可通过度规来得到克氏符的分量表达式
import numpy as np
import sympy
from einsteinpy.symbolic import MetricTensor, ChristoffelSymbols, RiemannCurvatureTensorr, th, phi = sympy.symbols('r theta phi')
# 球坐标度规
metric = np.diagflat([1,r**2,(r**2)*(sympy.sin(th)**2)])
m_obj.tensor()
# [[1, 0, 0], [0, r**2, 0], [0, 0, r**2*sin(theta)**2]]
ch = ChristoffelSymbols.from_metric(m_obj)
sympy.latex(ch.tensor())
打印出来如下
[[0000−r000−rsin2(θ)][01r01r0000−sin(θ)cos(θ)][001r00cos(θ)sin(θ)1rcos(θ)sin(θ)0]]\left[\begin{matrix}\left[\begin{matrix}0 & 0 & 0\\0 & - r & 0\\0 & 0 & - r \sin^{2}{\left(\theta \right)}\end{matrix}\right] & \left[\begin{matrix}0 & \frac{1}{r} & 0\\\frac{1}{r} & 0 & 0\\0 & 0 & - \sin{\left(\theta \right)} \cos{\left(\theta \right)}\end{matrix}\right] & \left[\begin{matrix}0 & 0 & \frac{1}{r}\\0 & 0 & \frac{\cos{\left(\theta \right)}}{\sin{\left(\theta \right)}}\\\frac{1}{r} & \frac{\cos{\left(\theta \right)}}{\sin{\left(\theta \right)}} & 0\end{matrix}\right]\end{matrix}\right] 0000−r000−rsin2(θ)0r10r10000−sin(θ)cos(θ)00r100sin(θ)cos(θ)r1sin(θ)cos(θ)0
这就是克氏符的真实面貌。
史瓦西时空
下面来搞一下史瓦西时空中的克氏符,而在此之前,先给出史瓦西时空的度规
t, r, th, phi = sympy.symbols("t r theta phi")
G, M, c, a = sympy.symbols("G M c a")
c2 = c**2
# using metric values of schwarschild space-time
# a is schwarzschild radius
list2d = np.diagflat([1-a/r, -1 / ((1 - (a/r)) * c2), -1 * (r**2)/c2,-1 * (r**2) * (sympy.sin(th)**2) / c2])
sch = MetricTensor(list2d, [t, r, th, phi])
sympy.latex(sch.tensor())
即其度规张量为
[−ar+10000−1c2(−ar+1)0000−r2c20000−r2sin2(θ)c2]\left[\begin{matrix}- \frac{a}{r} + 1 & 0 & 0 & 0\\0 & - \frac{1}{c^{2} \left(- \frac{a}{r} + 1\right)} & 0 & 0\\0 & 0 & - \frac{r^{2}}{c^{2}} & 0\\0 & 0 & 0 & - \frac{r^{2} \sin^{2}{\left(\theta \right)}}{c^{2}}\end{matrix}\right] −ra+10000−c2(−ra+1)10000−c2r20000−c2r2sin2(θ)
上式中,aaa为史瓦西半径,MMM为天体质量。
接下来,就可以请出史瓦西空间中的克氏符了
sch_ch = ChristoffelSymbols.from_metric(sch)
sympy.latex(sch_ch.tensor())
[[0a2r2(−ar+1)00a2r2(−ar+1)00000000000][−a(ac22r−c22)r20000a(ac22r−c22)c2r2(−ar+1)200002r(ac22r−c22)c200002r(ac22r−c22)sin2(θ)c2][0000001r001r00000−sin(θ)cos(θ)][00000001r000cos(θ)sin(θ)01rcos(θ)sin(θ)0]]\left[\begin{matrix}\left[\begin{matrix}0 & \frac{a}{2 r^{2} \left(- \frac{a}{r} + 1\right)} & 0 & 0\\\frac{a}{2 r^{2} \left(- \frac{a}{r} + 1\right)} & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{matrix}\right] \left[\begin{matrix}- \frac{a \left(\frac{a c^{2}}{2 r} - \frac{c^{2}}{2}\right)}{r^{2}} & 0 & 0 & 0\\0 & \frac{a \left(\frac{a c^{2}}{2 r} - \frac{c^{2}}{2}\right)}{c^{2} r^{2} \left(- \frac{a}{r} + 1\right)^{2}} & 0 & 0\\0 & 0 & \frac{2 r \left(\frac{a c^{2}}{2 r} - \frac{c^{2}}{2}\right)}{c^{2}} & 0\\0 & 0 & 0 & \frac{2 r \left(\frac{a c^{2}}{2 r} - \frac{c^{2}}{2}\right) \sin^{2}{\left(\theta \right)}}{c^{2}}\end{matrix}\right] & \left[\begin{matrix}0 & 0 & 0 & 0\\0 & 0 & \frac{1}{r} & 0\\0 & \frac{1}{r} & 0 & 0\\0 & 0 & 0 & - \sin{\left(\theta \right)} \cos{\left(\theta \right)}\end{matrix}\right] & \left[\begin{matrix}0 & 0 & 0 & 0\\0 & 0 & 0 & \frac{1}{r}\\0 & 0 & 0 & \frac{\cos{\left(\theta \right)}}{\sin{\left(\theta \right)}}\\0 & \frac{1}{r} & \frac{\cos{\left(\theta \right)}}{\sin{\left(\theta \right)}} & 0\end{matrix}\right]\end{matrix}\right] 02r2(−ra+1)a002r2(−ra+1)a00000000000−r2a(2rac2−2c2)0000c2r2(−ra+1)2a(2rac2−2c2)0000c22r(2rac2−2c2)0000c22r(2rac2−2c2)sin2(θ)000000r100r100000−sin(θ)cos(θ)0000000r1000sin(θ)cos(θ)0r1sin(θ)cos(θ)0
相关文章:

用Python获取史瓦西时空中克氏符的分量
文章目录三维球面坐标史瓦西时空三维球面坐标 Einsteinpy中提供了克氏符模型,可通过ChristoffelSymbols获取。简单起见,先以最直观的三维球面为例,来用Einsteinpy查看其克氏符的表达形式。 三维球面的度规张量可表示为 g001g11r2g22r2sin…...
QML编码约定
QML中的国际化: QML使用以下函数来将字符串标记为可翻译的 qsTr()qsTranslate()qsTrld()QT_TR_NOOP()QT_TRANSLATE_NOOP()QT_TRID_NOOP最常用的还是qsTr() string qsTr(string sourceText, string disambiguation&…...
【Linux】安装Linux操作系统具体步骤
1). 选择创建新的虚拟机 2). 选择"典型"配置 3). 选择"稍后安装操作系统(S)" 4). 选择"Linux"操作系统,"CentOS7 64位"版本 5). 设置虚拟机的名称及系统文件存放路径 6). 设置磁盘容量 7). 自定义硬件信息 8). 启动上述创建的新虚拟机…...
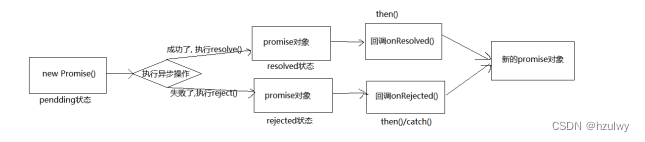
前端ES6异步编程技术——Promise使用
Promise是什么 官方的定义是:Promise是ES6新推出的用于进行异步编程的解决方案,旧方案是单纯使用回调函数来解决的。对于开发人员来说,我们把promise当作一个普通的对象即可,使用它可以用来封装一个异步操作并可以获取其成功/失败…...
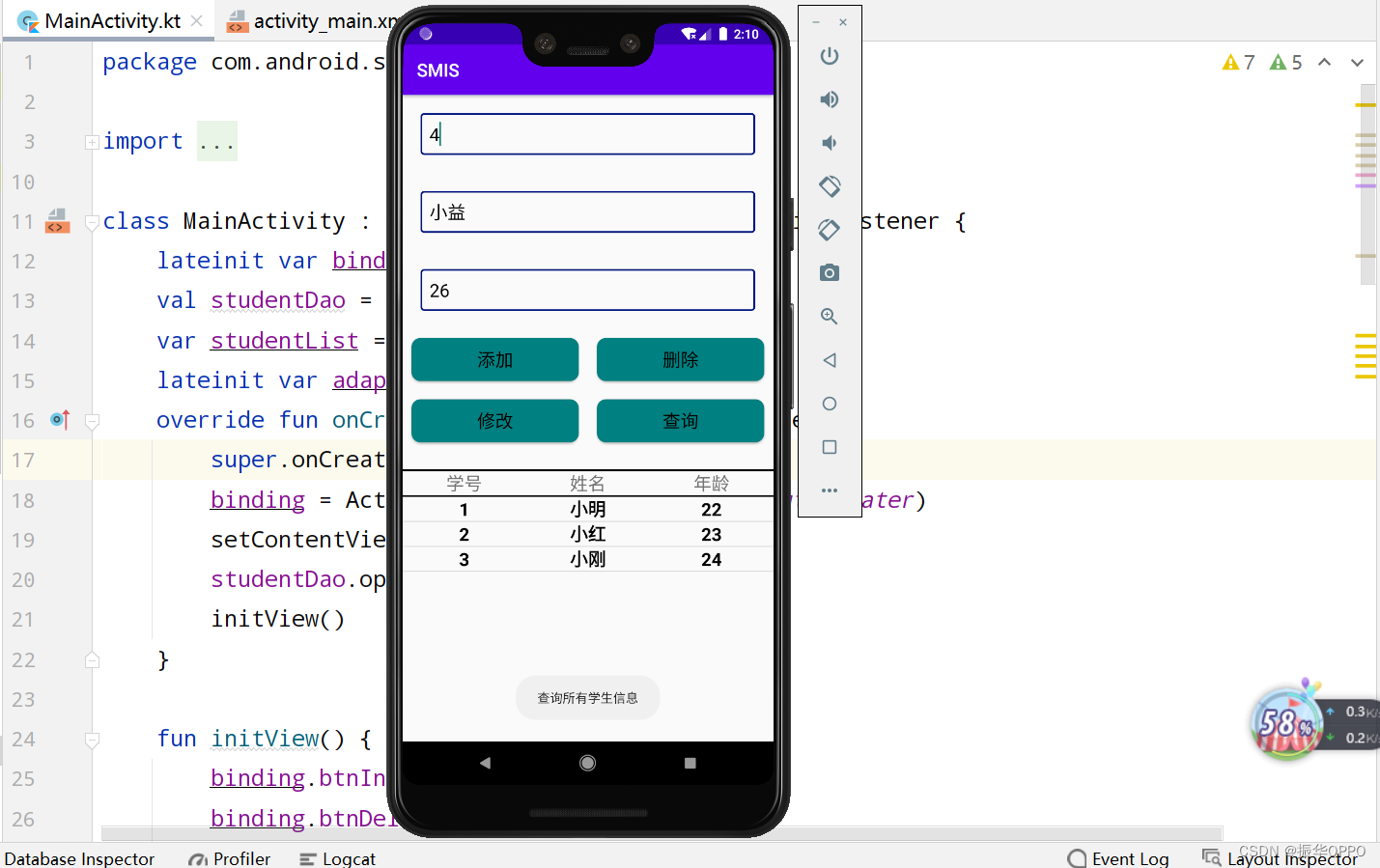
Kotlin实现简单的学生信息管理系统
文章目录一、实验内容二、实验步骤1、页面布局2、数据库3、登录活动4、增删改查三、运行演示四、实验总结五、源码下载一、实验内容 根据Android数据存储的内容,综合应用SharedPreferences和SQLite数据库实现一个用户信息管理系统,强化对SharedPreferen…...

413. 等差数列划分
413. 等差数列划分 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 nums ,返回数组 nums 中所有为等差数…...
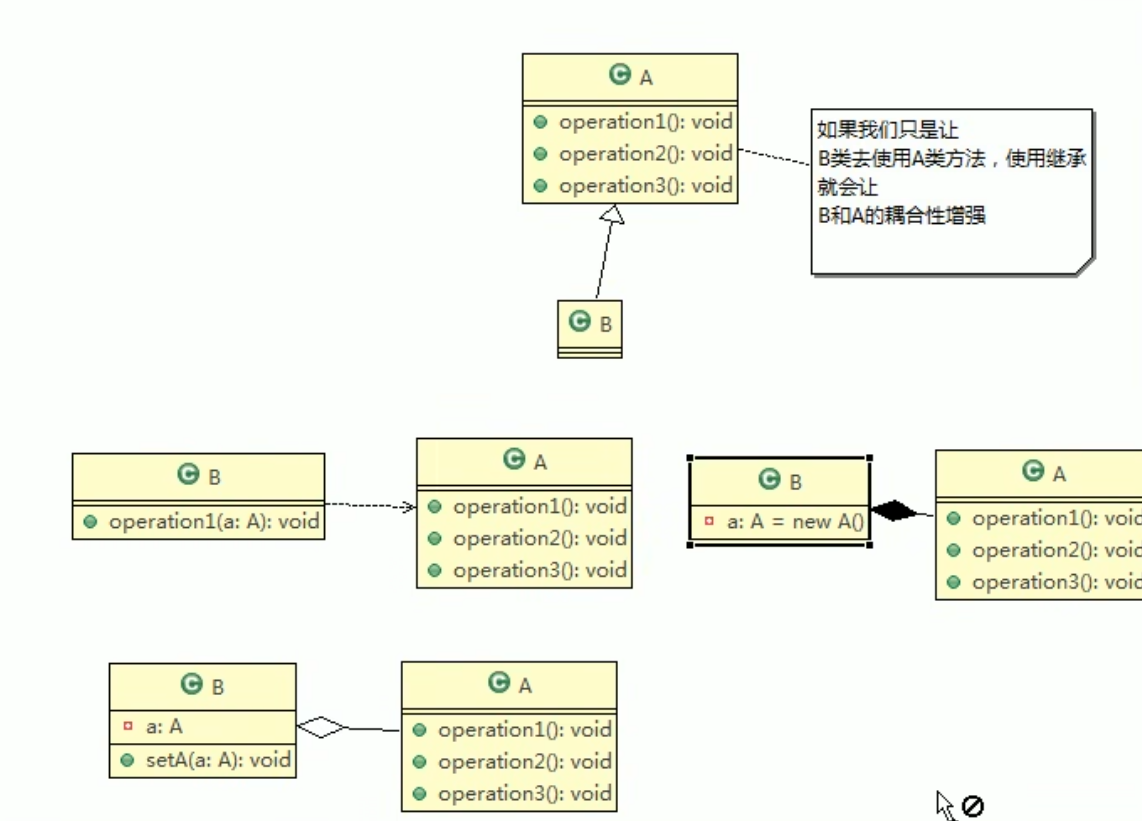
设计模式七大原则
一、设计模式概念 1.1 软件设计模式的产生背景 "设计模式"最初并不是出现在软件设计中,而是被用于建筑领域的设计中。 1977年美国著名建筑大师、加利福尼亚大学伯克利分校环境结构中心主任克里斯托夫亚历山大(Christopher Alexander&#x…...

【Mybatis系列】Mybatis常见的分页方法以及源码理解
Mybatis-Plus的selectPage 引入依赖 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.1</version></dependency>添加分页插件 Configuration public class My…...
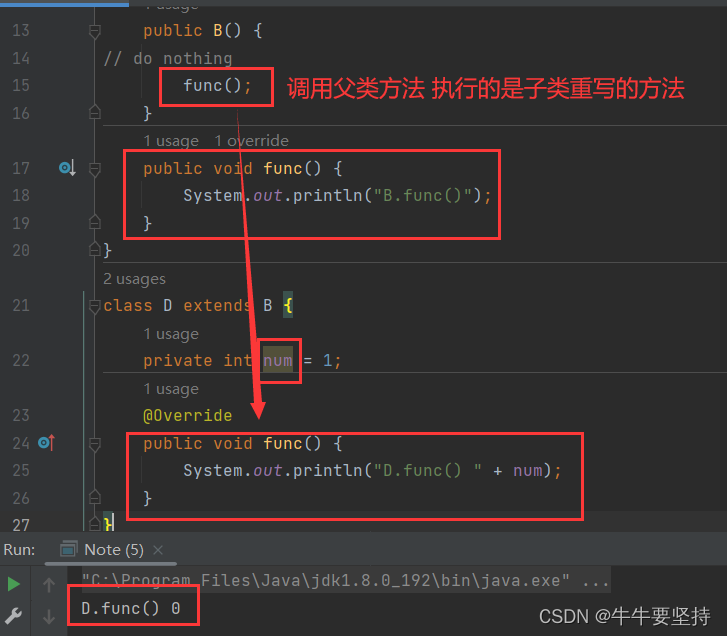
Java面向对象:多态特性的学习
本文介绍了Java面向对象多态特性, 多态的介绍. 多态的实现条件–1.发生继承.2.发生重写(重写与重载的区别)3.向上转型与向下转型.4.静态绑定和动态绑定5. 实现多态 举例总结多态的优缺点 避免在构造方法内调用被重写的方法… Java面向对象:多态特性的学习一.什么是多态?二.多态…...
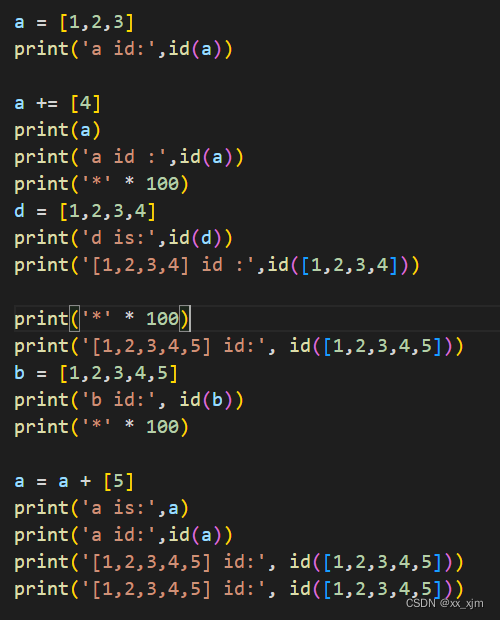
id函数 / 可变类型变量 / 不可变类型变量 / +=操作
前言 再说正文之前,需要大家先了解一下对象,指针和引用的含义,不懂得同学可以参考我上一篇博客“(12条消息) 引用是否有地址的讨论的_xx_xjm的博客-CSDN博客” 正文 一:python中一切皆对象 “python中一切皆对象”这句话我相信…...
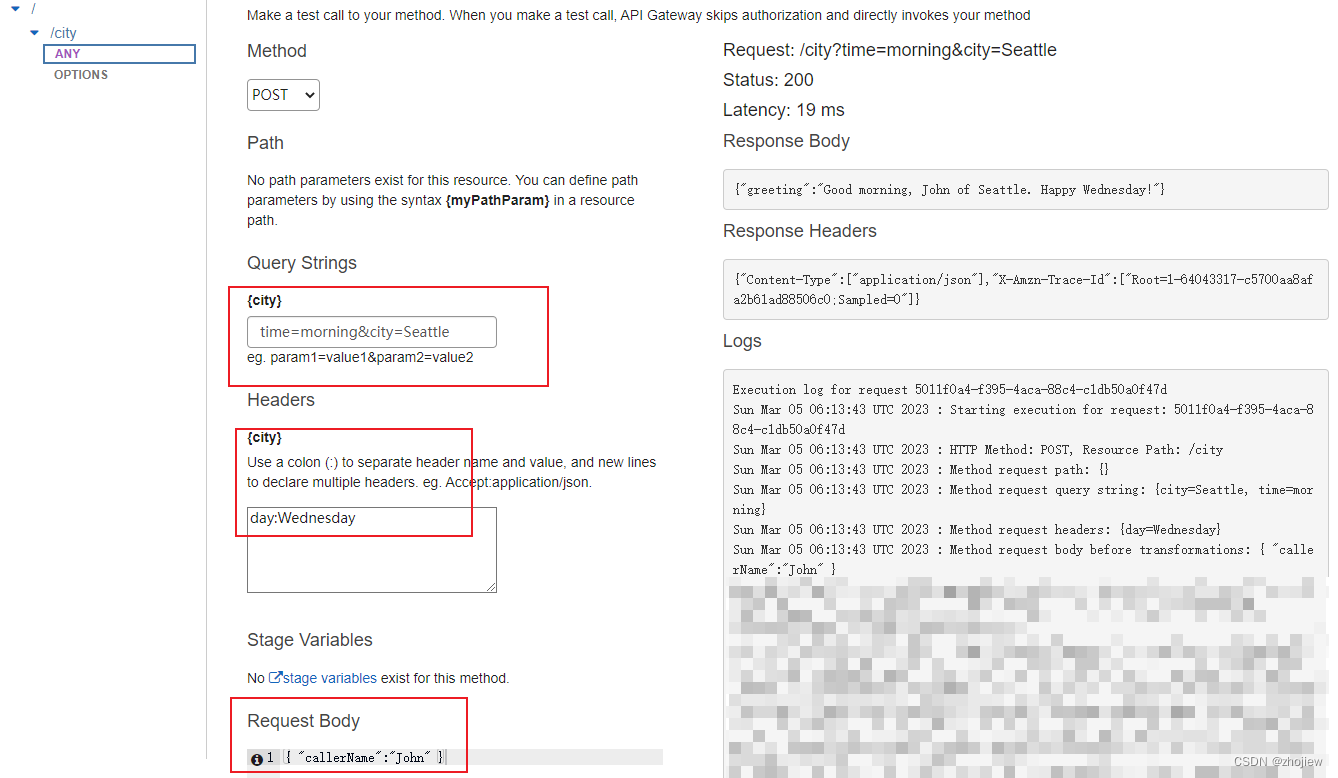
aws apigateway 使用apigateway集成lambda
参考资料 代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/api-gateway-create-api-as-simple-proxy-for-lambda.html非代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/getting-started-…...

Linux SPI 驱动实验
目录 一、Linux 下 SPI 驱动框架简介 1、SPI 主机驱动 2、SPI 设备驱动 SPI 设备数据收发处理流程 3、SPI 设备和驱动匹配过程 二、添加SPI 设备信息 1、添加 ICM20608 所使用的 IO 2、 在 ecspi3 节点追加 icm20608 子节点 三、编写 ICM20608 驱动 1、修改makefile…...
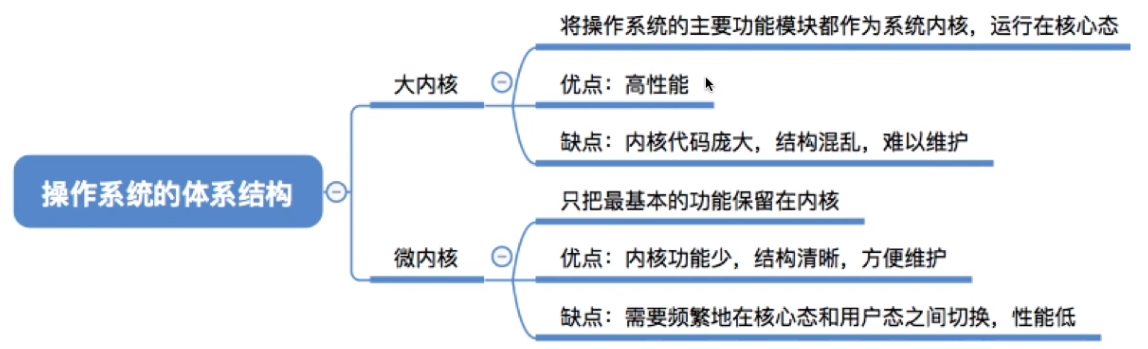
[1.4]计算机系统概述——操作系统的体系结构
第一章 计算机系统概述 操作系统的体系结构 大内核/单内核/宏内核微内核 通过之前的学习,我们知道计算机系统的层次结构是这样的。 但是操作系统的内部其实还可以再进一步地划分。 一部分是内核的功能,一部分是非内核的功能。 操作系统最核心的功能&…...
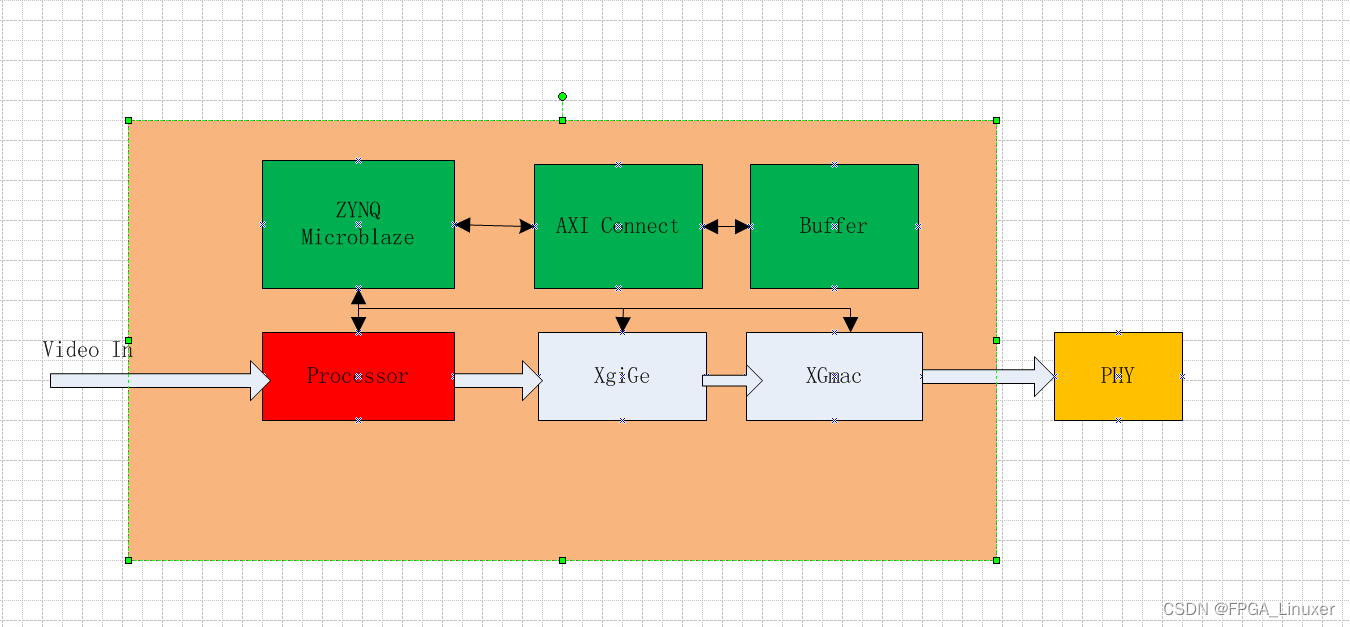
FPGA的GigE Vision IP相机图像采集方案设计,转换为千兆UDP,支持10G MAC
1 概述 GigE Vision是一个比较复杂的协议,要在FPGA中完全实现具有较大的难度。如果FPGA作为接收端希望实现GigE Vision相机的配置和图像采集功能,则只需要实现其中小部分功能即可。本文对原有GigE Vision协议的结构进行了裁剪,仅保留设备搜索…...
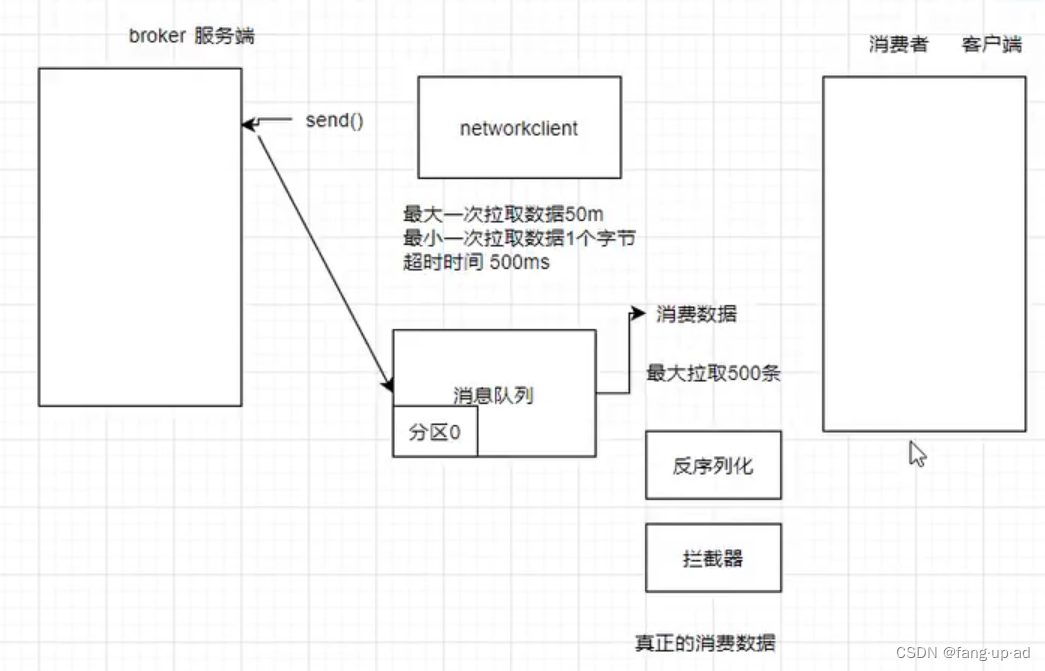
大数据相关面试题
linux 常见linux高级命令? top、iotopnetstatdf -hjmap -heaptarrpmps -efshell 用过的shell工具? awk Awk 命令详解 - 简书 awk是行处理器: 相比较屏幕处理的优点,在处理庞大文件时不会出现内存溢出或是处理缓慢的问题,通常用来…...

AI绘画第二步,抄作业复现超赞的效果!
上一篇,讲了如何安装AI绘画软件,但是装完后发现生成效果很渣!而网上那些效果都很赞。真的是理想很丰满,现实很骨感。今天就是来聊聊如何抄作业,最大程度的还原那些超赞的效果。换一种说法就是,教大家如何使…...

Python的并发编程
我们将一个正在运行的程序称为进程。每个进程都有它自己的系统状态,包含内存状态、打开文件列表、追踪指令执行情况的程序指针以及一个保存局部变量的调用栈。通常情况下,一个进程依照一个单序列控制流顺序执行,这个控制流被称为该进程的主线…...

【Linux】基本系统维护命令
😊😊作者简介😊😊 : 大家好,我是南瓜籽,一个在校大二学生,我将会持续分享C/C相关知识。 🎉🎉个人主页🎉🎉 : 南瓜籽的主页…...
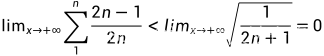
高数:数列的收敛
数列特点无限个数特定顺序数列和集合区别集合可以乱序,数列不行集合出现重复元素依然相同,数列出现新的重复元素就不相等[1,2,3,4][1,2,3,3,4]对集合来说相等,…...

不平凡的一天——
作者:指针不指南吗 专栏:个人日常记录 🐾或许会很慢,但是不可以停下来🐾 文章目录1.自我介绍2.上学期3.不凡的一天4.新学期写个博客,简单记录一下,新学期加油!!ÿ…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
