413. 等差数列划分
413. 等差数列划分
如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。
- 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
给你一个整数数组 nums ,返回数组 nums 中所有为等差数组的 子数组 个数。
子数组 是数组中的一个连续序列。
示例 1:
输入:nums = [1,2,3,4]
输出:3
解释:nums 中有三个子等差数组:[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。
示例 2:
输入:nums = [1]
输出:0
提示:
- 1<=nums.length<=50001 <= nums.length <= 50001<=nums.length<=5000
- −1000<=nums[i]<=1000-1000 <= nums[i] <= 1000−1000<=nums[i]<=1000
思路:
举个栗子:
A = [0, 1, 2, 3, 4]return: 6, for 3 arithmetic slices in A:[0, 1, 2],
[1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3, 4],
[ 1, 2, 3, 4],
[2, 3, 4]
dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。
当 A[i] - A[i-1] == A[i-1] - A[i-2],那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i],一样可以构成新的递增子区间。
dp[2] = 1[0, 1, 2]
dp[3] = dp[2] + 1 = 2[0, 1, 2, 3], // [0, 1, 2] 之后加一个 3[1, 2, 3] // 新的递增子区间
dp[4] = dp[3] + 1 = 3[0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4[1, 2, 3, 4], // [1, 2, 3] 之后加一个 4[2, 3, 4] // 新的递增子区间
综上,在 A[i] - A[i-1] == A[i-1] - A[i-2] 时,dp[i] = dp[i-1] + 1。
因为递增子区间不一定以最后一个元素为结尾,可以是任意一个元素结尾,因此需要返回 dp 数组累加的结果。
优化:
由于dp数组只需要知道上一个位置的数,所以可以用一个变量来记录就行了!
代码:(Java)
public class SeqPart {public static void main(String[] args) {// TODO Auto-generated method stubint[] nums = {1,2,3,8,9,10};System.out.println(numberOfArithmeticSlices(nums));}public static int numberOfArithmeticSlices(int[] nums) {if(nums == null ||nums.length < 3) {return 0;}int n = nums.length ;int total = 0;int dp = 0;for(int i = 2; i < n; i++) {if(nums[i] - nums[i - 1] == nums[i - 1] - nums[ i - 2]) {dp++;}else {dp = 0;}total += dp;}return total;}
}
复杂度分析:
- 时间复杂度:O(n),其中 n 是数组 nums的长度。
- 空间复杂度:O(1)。
注:仅供学习参考!
题目来源:力扣。
相关文章:

413. 等差数列划分
413. 等差数列划分 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 nums ,返回数组 nums 中所有为等差数…...
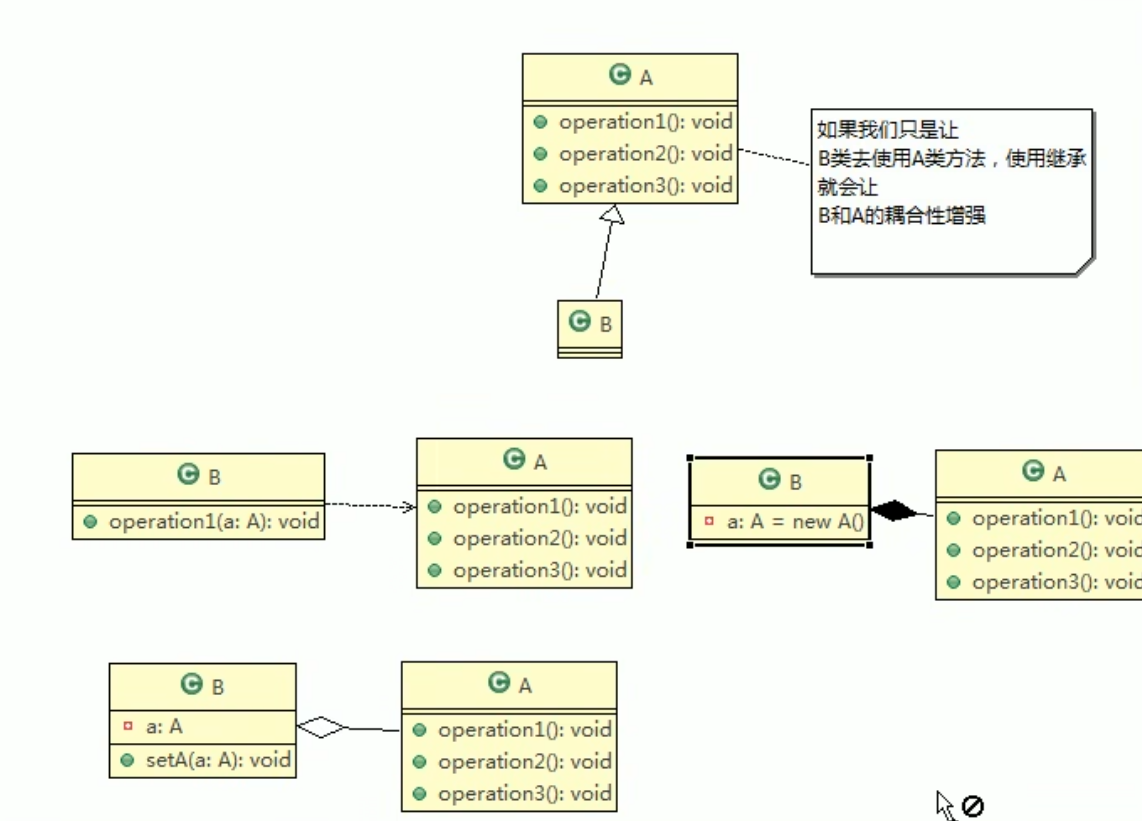
设计模式七大原则
一、设计模式概念 1.1 软件设计模式的产生背景 "设计模式"最初并不是出现在软件设计中,而是被用于建筑领域的设计中。 1977年美国著名建筑大师、加利福尼亚大学伯克利分校环境结构中心主任克里斯托夫亚历山大(Christopher Alexander&#x…...

【Mybatis系列】Mybatis常见的分页方法以及源码理解
Mybatis-Plus的selectPage 引入依赖 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.1</version></dependency>添加分页插件 Configuration public class My…...
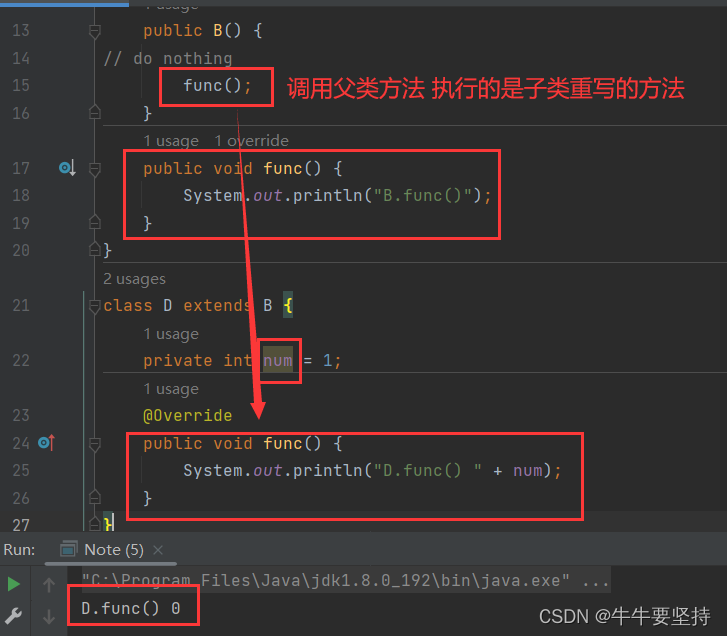
Java面向对象:多态特性的学习
本文介绍了Java面向对象多态特性, 多态的介绍. 多态的实现条件–1.发生继承.2.发生重写(重写与重载的区别)3.向上转型与向下转型.4.静态绑定和动态绑定5. 实现多态 举例总结多态的优缺点 避免在构造方法内调用被重写的方法… Java面向对象:多态特性的学习一.什么是多态?二.多态…...
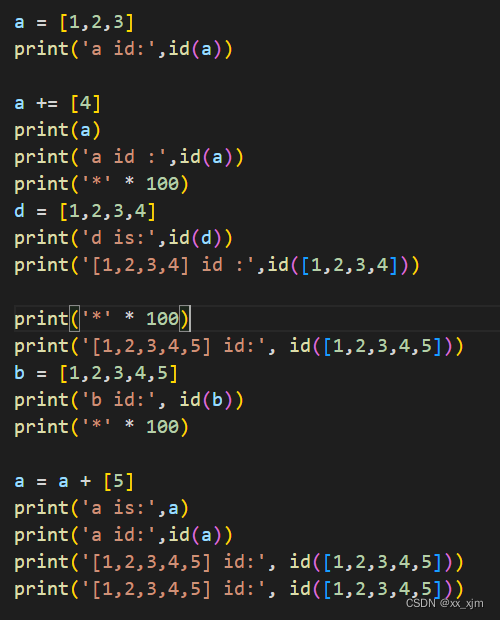
id函数 / 可变类型变量 / 不可变类型变量 / +=操作
前言 再说正文之前,需要大家先了解一下对象,指针和引用的含义,不懂得同学可以参考我上一篇博客“(12条消息) 引用是否有地址的讨论的_xx_xjm的博客-CSDN博客” 正文 一:python中一切皆对象 “python中一切皆对象”这句话我相信…...
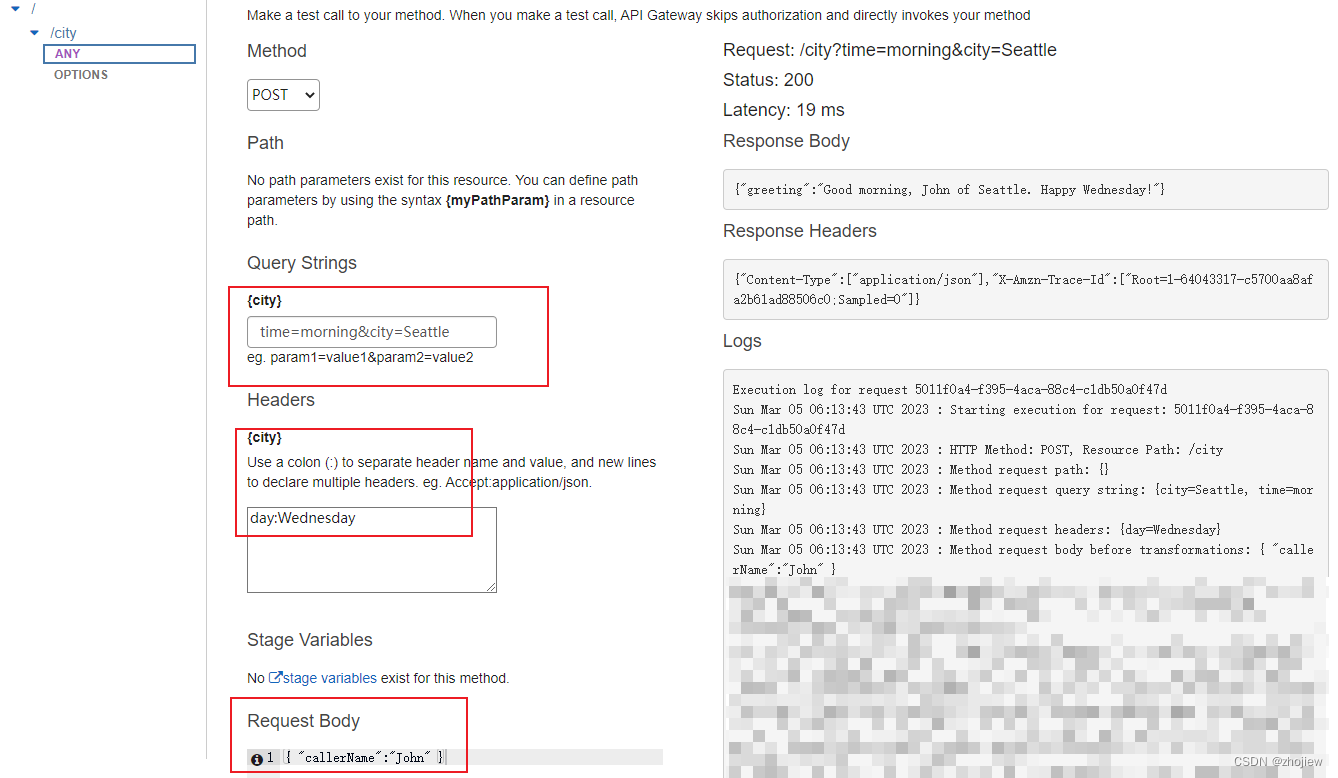
aws apigateway 使用apigateway集成lambda
参考资料 代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/api-gateway-create-api-as-simple-proxy-for-lambda.html非代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/getting-started-…...

Linux SPI 驱动实验
目录 一、Linux 下 SPI 驱动框架简介 1、SPI 主机驱动 2、SPI 设备驱动 SPI 设备数据收发处理流程 3、SPI 设备和驱动匹配过程 二、添加SPI 设备信息 1、添加 ICM20608 所使用的 IO 2、 在 ecspi3 节点追加 icm20608 子节点 三、编写 ICM20608 驱动 1、修改makefile…...
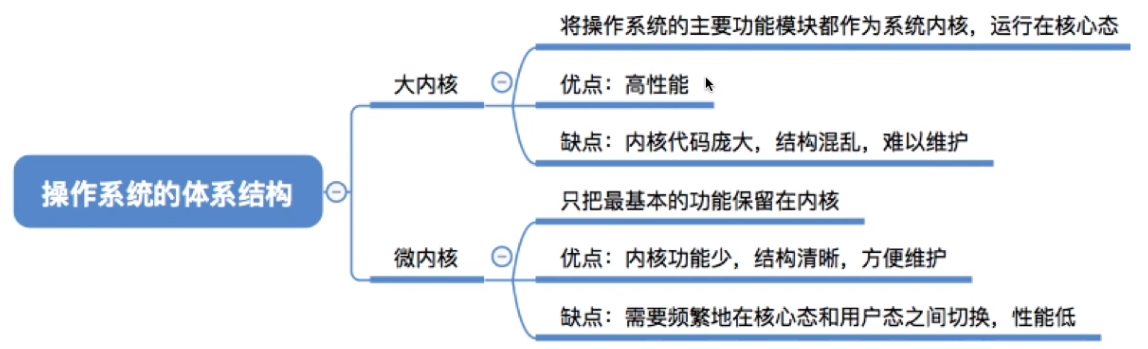
[1.4]计算机系统概述——操作系统的体系结构
第一章 计算机系统概述 操作系统的体系结构 大内核/单内核/宏内核微内核 通过之前的学习,我们知道计算机系统的层次结构是这样的。 但是操作系统的内部其实还可以再进一步地划分。 一部分是内核的功能,一部分是非内核的功能。 操作系统最核心的功能&…...
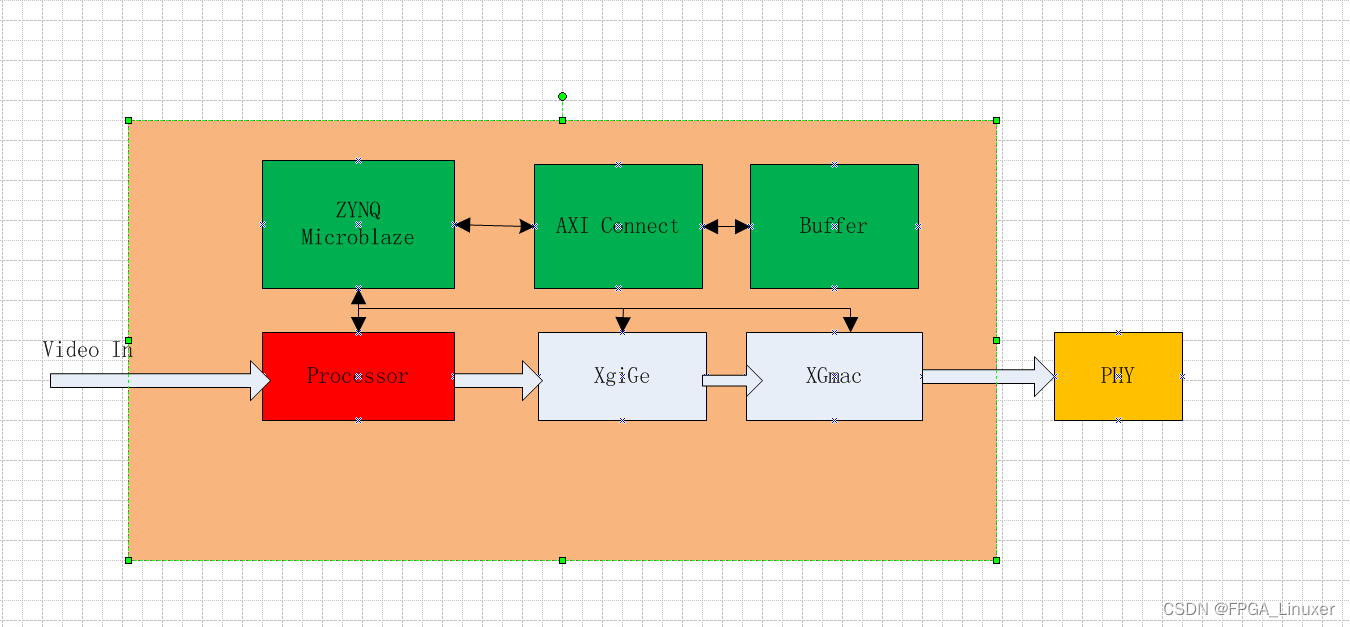
FPGA的GigE Vision IP相机图像采集方案设计,转换为千兆UDP,支持10G MAC
1 概述 GigE Vision是一个比较复杂的协议,要在FPGA中完全实现具有较大的难度。如果FPGA作为接收端希望实现GigE Vision相机的配置和图像采集功能,则只需要实现其中小部分功能即可。本文对原有GigE Vision协议的结构进行了裁剪,仅保留设备搜索…...
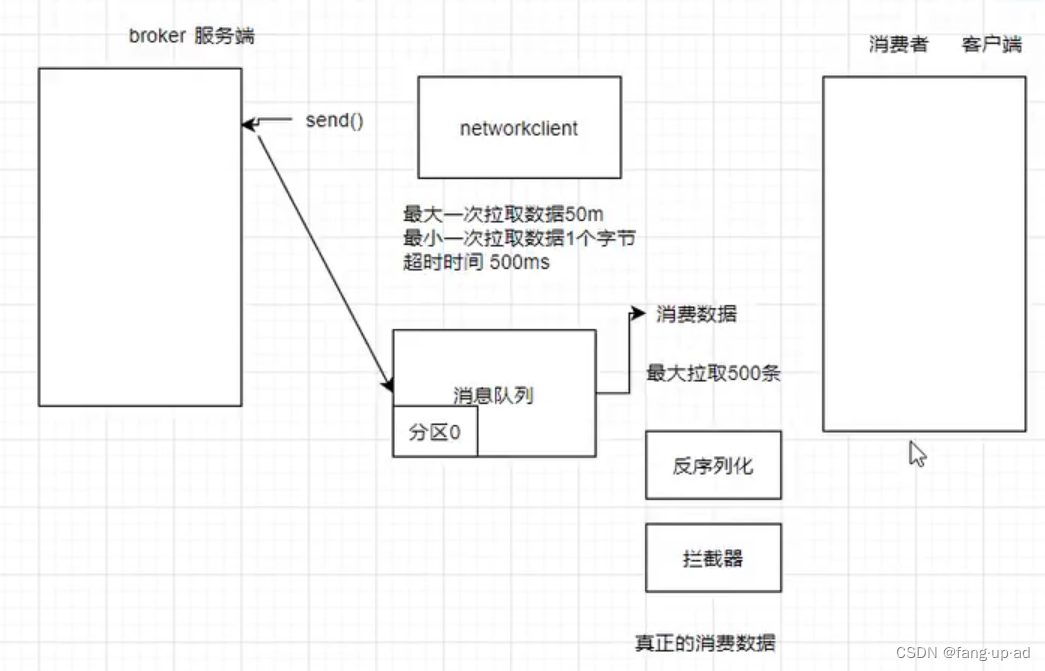
大数据相关面试题
linux 常见linux高级命令? top、iotopnetstatdf -hjmap -heaptarrpmps -efshell 用过的shell工具? awk Awk 命令详解 - 简书 awk是行处理器: 相比较屏幕处理的优点,在处理庞大文件时不会出现内存溢出或是处理缓慢的问题,通常用来…...

AI绘画第二步,抄作业复现超赞的效果!
上一篇,讲了如何安装AI绘画软件,但是装完后发现生成效果很渣!而网上那些效果都很赞。真的是理想很丰满,现实很骨感。今天就是来聊聊如何抄作业,最大程度的还原那些超赞的效果。换一种说法就是,教大家如何使…...

Python的并发编程
我们将一个正在运行的程序称为进程。每个进程都有它自己的系统状态,包含内存状态、打开文件列表、追踪指令执行情况的程序指针以及一个保存局部变量的调用栈。通常情况下,一个进程依照一个单序列控制流顺序执行,这个控制流被称为该进程的主线…...

【Linux】基本系统维护命令
😊😊作者简介😊😊 : 大家好,我是南瓜籽,一个在校大二学生,我将会持续分享C/C相关知识。 🎉🎉个人主页🎉🎉 : 南瓜籽的主页…...
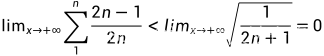
高数:数列的收敛
数列特点无限个数特定顺序数列和集合区别集合可以乱序,数列不行集合出现重复元素依然相同,数列出现新的重复元素就不相等[1,2,3,4][1,2,3,3,4]对集合来说相等,…...

不平凡的一天——
作者:指针不指南吗 专栏:个人日常记录 🐾或许会很慢,但是不可以停下来🐾 文章目录1.自我介绍2.上学期3.不凡的一天4.新学期写个博客,简单记录一下,新学期加油!!ÿ…...

【Java基础】Map遍历的5种方式
目录 创建一个集合 方式一:Iterator 迭代器遍历 map.entrySet().iterator(); map.keySet().iterator(); 方式二:For Each方式遍历 map.forEach(BiConsumer action) 方式三:获取Collection集合 map.values().forEach() 方式四&#x…...
第十四届蓝桥杯三月真题刷题训练——第 2 天
目录 题目1:奇数倍数 代码: 题目2:求值 代码: 题目3:求和 代码: 题目4:数位排序 代码: 题目1:奇数倍数 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即…...

自然语言处理历史最全预训练模型(部署)汇集分享
什么是预训练模型?预练模型是其他人为解决类似问题而创建的且已经训练好的模型。代替从头开始建立模型来解决类似的问题,我们可以使用在其他问题上训练过的模型作为起点。预训练的模型在相似的应用程序中可能不是100%准确的。本文整理了自然语…...
csdn写文章自定义表格怎么做
前言 CSDN写文章时,经常会用到表格,不同于Word文档中直接插入表格(自定义几行几列),使用CSDN自带的md文本编辑器时,很难快速插入想要的表格样式,追究原因,也是因为md的语法问题&…...
)
Pytorch处理数据与训练网络问题汇总(协同训练)
基础语法 模型训练 【Swin-Unet】官方代码预训练权重加载函数load_from() 实际上由于SwinUnet是一个encoder-decoder对称的结构,因此加载权重时,作者并没有像通常那样仅仅加载encoder部分而不加载decoder部分,而是同时将encoder的权重对称地…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...
