[Python] 什么是逻辑回归模型?使用scikit-learn中的LogisticRegression来解决乳腺癌数据集上的二分类问题
什么是线性回归和逻辑回归?
线性回归是一种用于解决回归问题的统计模型。它通过建立自变量(或特征)与因变量之间的线性关系来预测连续数值的输出。线性回归的目标是找到一条直线(或超平面),使得预测值与观察值之间的残差(误差)最小化。这条直线或超平面可以用来表示输入变量与输出变量之间的关系。线性回归假设输入特征与输出之间存在线性关系,并且残差服从正态分布。线性回归适用于预测和推断,常见应用包括房价预测、销售预测、股票预测等。
线性回归方程式:
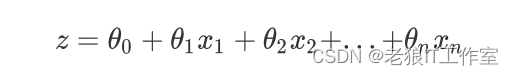
被统称为模型的参数,其中 被称为截距(intercept),
1 ~
n被称为系数(coefficient),这个表达式,其实就和我 们小学时就无比熟悉的 是同样的性质。我们可以使用矩阵来表示这个方程,其中x被看做是一 个列矩阵,
被看作是一个行矩阵,则有:
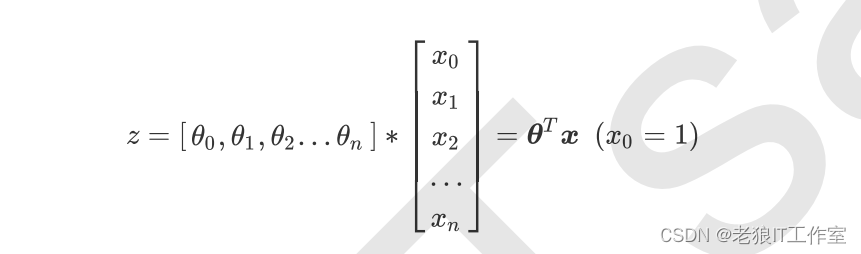
线性回归的任务,就是构造一个预测函数 Z 来映射输入的特征矩阵x和标签值y的线性关系,而构造预测函数的核心就是找出模型的参数T和
0,著名的最小二乘法就是用来求解线性回归中参数的数学方法。
通过函数 ,线性回归使用输入的特征矩阵 X 来输出一组连续型的标签值 y_pred,以完成各种预测连续型变量的任务 (比如预测产品销量,预测股价等等)。
那如果我们的标签是离散型变量,尤其是,如果是满足0-1分布的离散型变量,我们要怎么办呢?我们可以通过引入联系函数(link function),将线性回归方程z变换为g(z),并且令g(z)的值分布在(0,1)之间,且当g(z)接近0时样本的标签为类别0,当g(z)接近1时样本的标签为类别1,这样就得到了一个分类模型。而这个联系函数对于逻辑回归来说,就是Sigmoid函数:
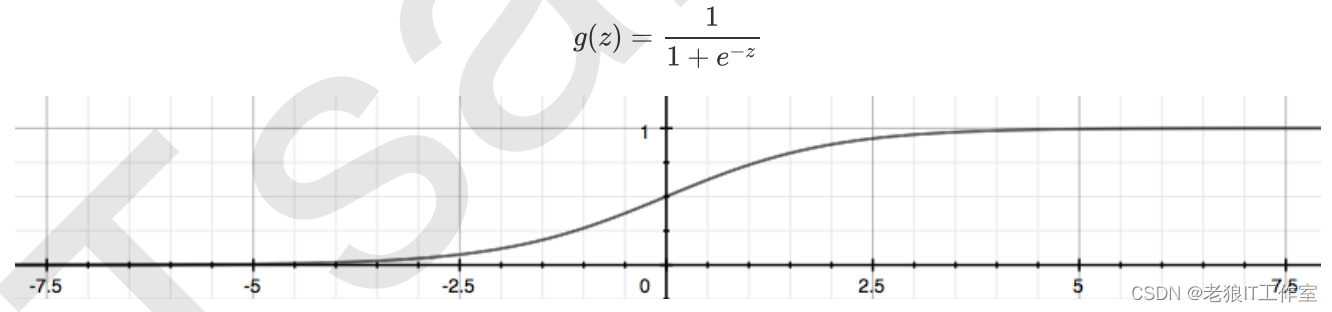
Sigmoid函数是一个S型的函数,当自变量z趋近正无穷时,因变量g(z)趋近于1,而当z趋近负无穷时,g(z)趋近 于0,它能够将任何实数映射到(0,1)区间,使其可用于将任意值函数转换为更适合二分类的函数。 因为这个性质,Sigmoid函数也被当作是归一化的一种方法,与我们之前学过的MinMaxSclaer同理,是属于 数据预处理中的“缩放”功能,可以将数据压缩到[0,1]之内。区别在于,MinMaxScaler归一化之后,是可以取 到0和1的(最大值归一化后就是1,最小值归一化后就是0),但Sigmoid函数只是无限趋近于0和1。
线性回归中 Z = T X,于是我们将
T带入,就得到了二元逻辑回归模型的一般形式:

而g(z)就是我们逻辑回归返回的标签值。此时, y(x) 的取值都在[0,1]之间,因此y(x) 和 1 - y(x) 相加必然为1。如果我们令y(x) 除以 1 - y(x) 可以得到形似几率(odds)的 y(x) / (1 - y(x)),在此基础上取对数,可以很容易就得到:

不难发现,g(z)的形似几率取对数的本质其实就是我们的线性回归z,我们实际上是在对线性回归模型的预测结果取对数几率来让其的结果无限逼近0和1。因此,其对应的模型被称为”对数几率回归“(logistic Regression),也就是我们的逻辑回归,这个名为“回归”却是用来做分类工作的分类器。
逻辑回归是一种用于解决分类问题的统计模型。它通过将特征与相应的标签之间的关系建模为一个逻辑函数来进行预测。逻辑回归的输出是一个概率值,表示样本属于某个类别的可能性。通常情况下,当输出概率大于某个阈值时,样本被分类为正例,否则分类为负例。逻辑回归可以处理二分类问题和多分类问题。
逻辑回归是一个受工业商业热爱,使用广泛的模型,因为它有着不可替代 的优点:
1. 逻辑回归对线性关系的拟合效果好到丧心病狂,特征与标签之间的线性关系极强的数据,比如金融领域中的信用卡欺诈,评分卡制作,电商中的营销预测等等相关的数据,都是逻辑回归的强项。虽然现在有了梯度提升树GDBT,比逻辑回归效果更好,也被许多数据咨询公司启用,但逻辑回归在金融领域,尤其是银行业中的统治地位依然不可动摇(相对的,逻辑回归在非线性数据的效果很多时候比瞎猜还不如,所以如果你已经知道数据之间的联系是非线性的,千万不要迷信逻辑回归)。
2. 逻辑回归计算快:对于线性数据,逻辑回归的拟合和计算都非常快,计算效率优于SVM和随机森林,亲测表示在大型数据上尤其能够看得出区别。
3. 逻辑回归返回的分类结果不是固定的0,1,而是以小数形式呈现的类概率数字:我们因此可以把逻辑回归返回的结果当成连续型数据来利用。比如在评分卡制作时,我们不仅需要判断客户是否会违约,还需要给出确定的”信用分“,而这个信用分的计算就需要使用类概率计算出的对数几率,而决策树和随机森林这样的分类器,可以产出分类结果,却无法帮助我们计算分数(当然,在sklearn中,决策树也可以产生概率,使用接口 predict_proba调用就好,但一般来说,正常的决策树没有这个功能)。
另外,逻辑回归还有抗噪能力强的优点。福布斯杂志在讨论逻辑回归的优点时,甚至有着“技术上来说,最佳模型的AUC面积低于0.8时,逻辑回归非常明显优于树模型”的说法。并且,逻辑回归在小数据集上表现更好,在大型的数据集上,树模型有着更好的表现。 由此,我们已经了解了逻辑回归的本质,它是一个返回对数几率的,在线性数据上表现优异的分类器,它主要被应用在金融领域。其数学目的是求解能够让模型最优化的参数的值,并基于参数
和特征矩阵计算出逻辑回归的结果 y(x)。注意:虽然我们熟悉的逻辑回归通常被用于处理二分类问题,但逻辑回归也可以做多分类。
sklearn中的逻辑回归

API Reference — scikit-learn 1.4.0 documentation

linear_model.LogisticRegression
sklearn.linear_model.LogisticRegression — scikit-learn 1.4.0 documentation
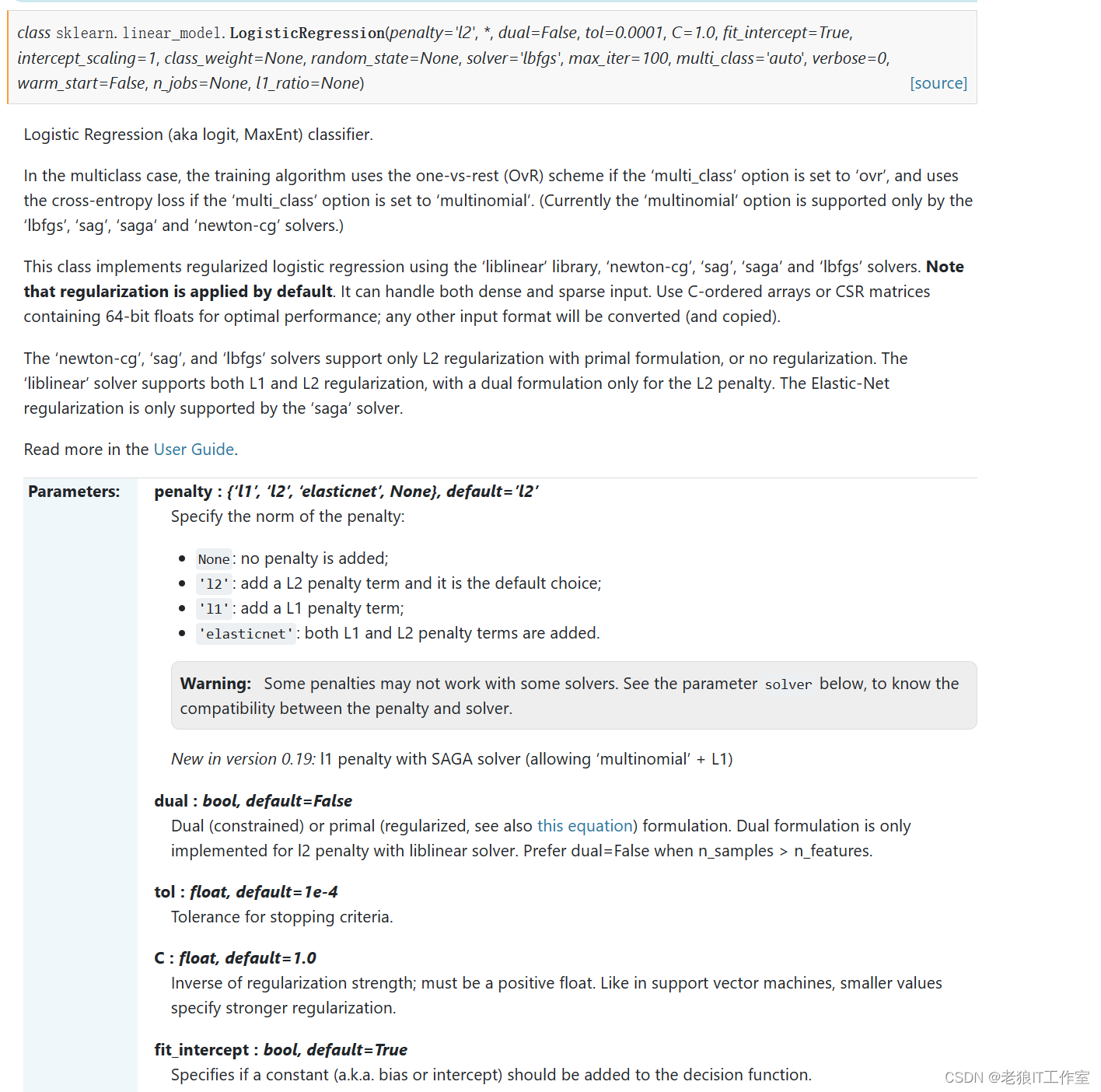

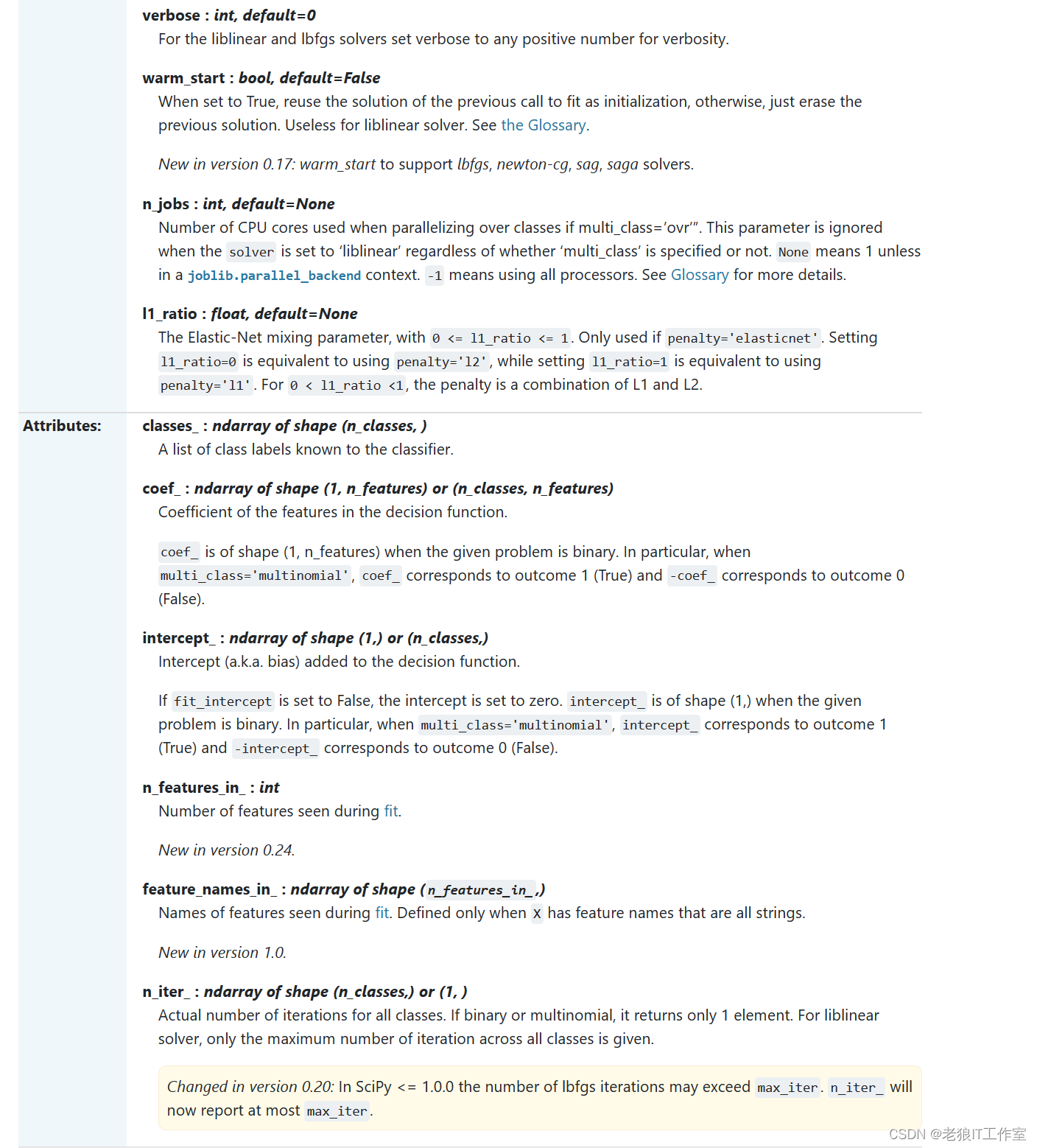
二元逻辑回归的损失函数
我们使用”损失函数“这个评估指标,来衡量参数 的优劣,即这一组参数能否使模型在训练集上表现优异。 如果用一组参数建模后,模型在训练集上表现良好,那我们就说模型表现的规律与训练集数据的规律一致,拟合过 程中的损失很小,损失函数的值很小,这一组参数就优秀;相反,如果模型在训练集上表现糟糕,损失函数就会很 大,模型就训练不足,效果较差,这一组参数也就比较差。即是说,我们在求解参数时,追求损失函数最小,让模型在训练数据上的拟合效果最优,即预测准确率尽量靠近100%。
逻辑回归的损失函数是由最大似然法来推导出来的,具体结果可以写作:

由于我们追求损失函数的最小值,让模型在训练集上表现最优,可能会引发另一个问题:如果模型在训练集上表示优秀,却在测试集上表现糟糕,模型就会过拟合。虽然逻辑回归和线性回归是天生欠拟合的模型,但我们还是需要控制过拟合的技术来帮助我们调整模型,对逻辑回归中过拟合的控制,通过正则化来实现。
重要参数penalty & C (正则化)


正则化是用来防止模型过拟合的过程,常用的有L1正则化和L2正则化两种选项,分别通过在损失函数后加上参数向 量 的L1范式和L2范式的倍数来实现。这个增加的范式,被称为“正则项”,也被称为"惩罚项"。损失函数改变,基 于损失函数的最优化来求解的参数取值必然改变,我们以此来调节模型拟合的程度。其中L1范数表现为参数向量中的每个参数的绝对值之和,L2范数表现为参数向量中的每个参数的平方和的开方值。

 L1正则化和L2正则化虽然都可以控制过拟合,但它们的效果并不相同。当正则化强度逐渐增大(即C逐渐变小), 参数的取值会逐渐变小,但L1正则化会将参数压缩为0,L2正则化只会让参数尽量小,不会取到0。
L1正则化和L2正则化虽然都可以控制过拟合,但它们的效果并不相同。当正则化强度逐渐增大(即C逐渐变小), 参数的取值会逐渐变小,但L1正则化会将参数压缩为0,L2正则化只会让参数尽量小,不会取到0。
在L1正则化在逐渐加强的过程中,携带信息量小的、对模型贡献不大的特征的参数,会比携带大量信息的、对模型 有巨大贡献的特征的参数更快地变成0,所以L1正则化本质是一个特征选择的过程,掌管了参数的“稀疏性”。L1正 则化越强,参数向量中就越多的参数为0,参数就越稀疏,选出来的特征就越少,以此来防止过拟合。因此,如果特征量很大,数据维度很高,我们会倾向于使用L1正则化。由于L1正则化的这个性质,逻辑回归的特征选择可以由 Embedded 嵌入法来完成。
相对的,L2正则化在加强的过程中,会尽量让每个特征对模型都有一些小的贡献,但携带信息少,对模型贡献不大的特征的参数会非常接近于0。通常来说,如果我们的主要目的只是为了防止过拟合,选择L2正则化就足够了。但 是如果选择L2正则化后还是过拟合,模型在未知数据集上的效果表现很差,就可以考虑L1正则化。
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_scoredata = load_breast_cancer()
X = data.data
y = data.target
print('feature names:', data.feature_names)
print('target names:', data.target_names)
print('X:', X[0:5])
print('y:', y[0:5])
data.data.shapelrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)
#逻辑回归的重要属性coef_,查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_(lrl1.coef_ != 0).sum(axis=1)lrl2 = lrl2.fit(X,y)
lrl2.coef_

可以看见,当我们选择L1正则化的时候,许多特征的参数都被设置为了0,这些特征在真正建模的时候,就不会出现在我们的模型当中了,而L2正则化则是对所有的特征都给出了参数。
究竟哪个正则化的效果更好呢?还是都差不多?
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1,19):lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)lrl1 = lrl1.fit(Xtrain,Ytrain)l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))lrl2 = lrl2.fit(Xtrain,Ytrain)l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示,右下角
plt.show()
可见,至少在我们的乳腺癌数据集下,两种正则化的结果区别不大。但随着C的逐渐变大,正则化的强度越来越小,模型在训练集和测试集上的表现都呈上升趋势,直到C=0.8左右,训练集上的表现依然在走高,但模型在未知数据集上的表现开始下跌,这时候就是出现了过拟合。我们可以认为,C设定为0.9会比较好。在实际使用时,基本就默认使用l2正则化,如果感觉到模型的效果不好,那就换L1试试看。
重要参数max_iter(solver最大迭代次数)

参数max_iter是逻辑回归模型的最大迭代次数。默认情况下,它的值是100。
逻辑回归模型通过最大化似然函数来估计模型的参数。在迭代的过程中,模型会不断调整参数以最大化似然函数,直到收敛为止。max_iter参数用于指定最大迭代次数,即模型在达到该次数之前会进行迭代调整参数。
如果模型在达到最大迭代次数之前已经收敛,则训练会提前停止。否则,会发出一个警告并返回最后一次迭代的结果。
max_iter的值需要根据具体的数据集和模型复杂度来进行调整。如果模型在默认迭代次数内没有收敛,可以适当增加max_iter的值。与此同时,也要注意控制迭代次数,以避免过度拟合或训练时间过长的问题。
逻辑回归的数学目的是求解能够让模型最优化的参数
的值,即求解能够让损失函数最小化的
的值, 而这个求解过程,对于二元逻辑回归来说,有多种方法可以选择,最常见的有梯度下降法(Gradient Descent),坐标轴下降法(Coordinate Descent),牛顿法(Newton-Raphson method)等,每种方法都涉及复杂的数学原理,但这些计算在执行的任务其实是类似的。
重要参数solver(使用的优化算法)

sklearn.linear_model.LogisticRegression中的参数solver用于指定逻辑回归模型的优化算法。下面是solver参数的详细说明:
-
"newton-cg": 使用牛顿共轭梯度法进行优化。适用于较小的数据集,对特征数量敏感。
-
"lbfgs": 使用拟牛顿法的Limited-memory Broyden-Fletcher-Goldfarb-Shanno算法进行优化。适用于较小的数据集。
-
"liblinear": 使用坐标下降法进行优化。适用于较大的数据集,支持L1和L2正则化。
-
"sag": 使用随机平均梯度法进行优化。适用于大规模数据集。
-
"saga": 与"sag"类似,但支持弹性网络正则化。适用于大规模数据集。
不同的solver对模型的收敛速度和性能可能会有所影响。在选择solver时,可以考虑数据集的规模、特征数量以及是否需要使用正则化等因素来选择合适的优化算法。
重要参数class_weight(样本不平衡)

class_weight用于指定不同类别的权重。默认情况下,所有类别的权重都是相等的。
逻辑回归是一种二分类模型,但也可以用于多分类问题。当数据集中的类别不平衡时,即某些类别的样本数量远大于其他类别时,设置class_weight参数可以帮助模型更好地处理不平衡的情况。
class_weight参数可以接受以下几种输入形式:
- 'balanced':自动根据训练集中各类别的样本数量来计算权重。较少样本的类别将会有较高的权重。
- 字典:用于指定每个类别的权重。字典的键为类别的索引或标签,值为对应的权重。
- 数组:用于指定每个类别的权重。数组的索引对应类别的索引或标签,值为对应的权重。
设置class_weight参数可以提高模型对少数类别的识别能力,从而避免模型过度依赖多数类别。
参考资料
【技术干货】菜菜的机器学习sklearn
相关文章:

[Python] 什么是逻辑回归模型?使用scikit-learn中的LogisticRegression来解决乳腺癌数据集上的二分类问题
什么是线性回归和逻辑回归? 线性回归是一种用于解决回归问题的统计模型。它通过建立自变量(或特征)与因变量之间的线性关系来预测连续数值的输出。线性回归的目标是找到一条直线(或超平面),使得预测值与观…...

那些不输于乙游男主人设的国漫男主
最近乙游的势头越来越猛,新宠旧爱一起上阵,叫人应接不暇。在二次元的世界里,乙游男主们凭借着超凡的魅力,成为了无数少女心中的理想对象。他们或冷酷、或温柔、或阳光、或神秘,每一个角色都有着独特的性格和故事。 乙游…...
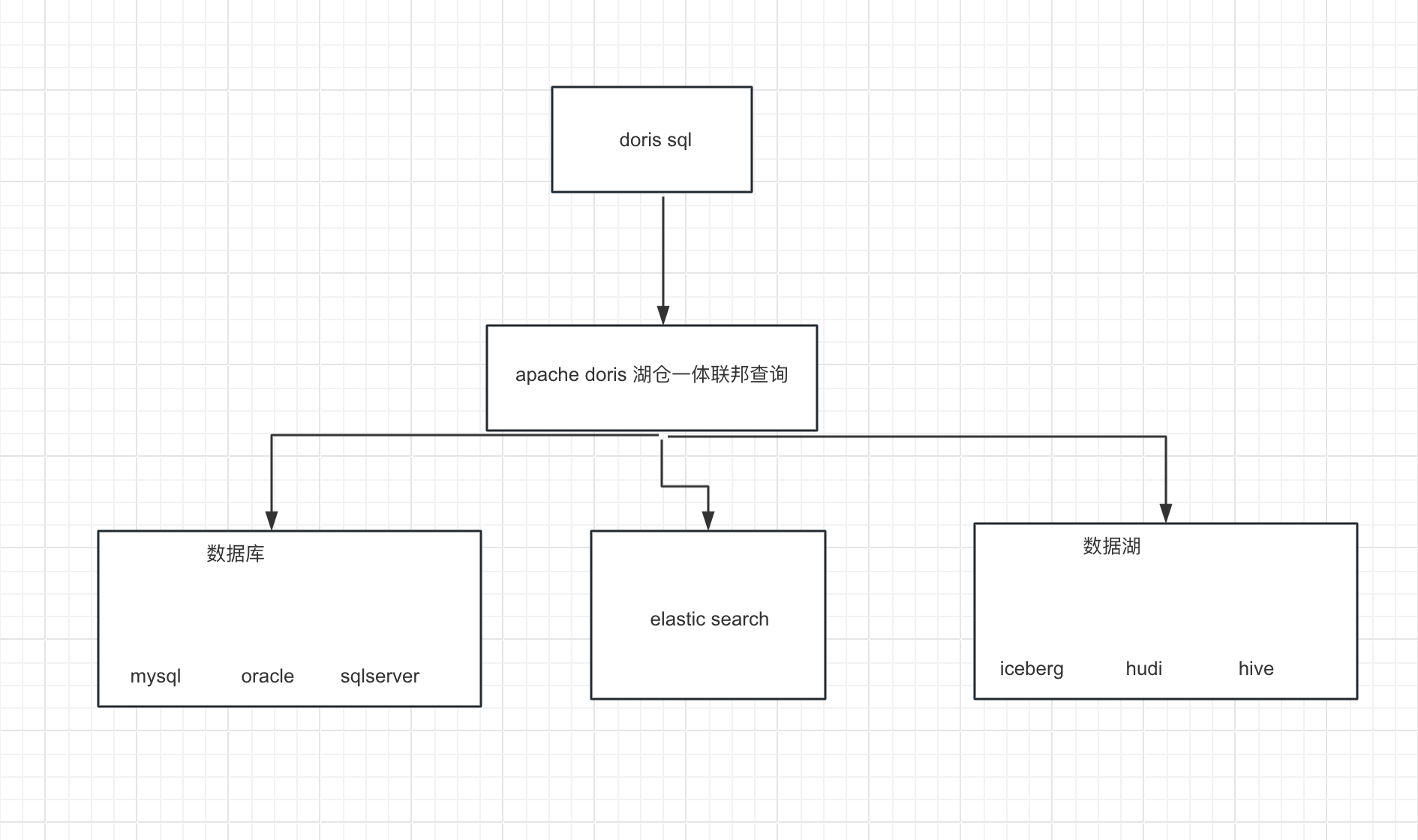
Apache Doris 整合 FLINK CDC + Iceberg 构建实时湖仓一体的联邦查询
1概况 本文展示如何使用 Flink CDC Iceberg Doris 构建实时湖仓一体的联邦查询分析,Doris 1.1版本提供了Iceberg的支持,本文主要展示Doris和Iceberg怎么使用,大家按照步骤可以一步步完成。完整体验整个搭建操作的过程。 2系统架构 我们整…...
关于华为应用市场上架,申请权限未告知目的被驳回问题的简单处理方式
关于华为应用市场上架过程中出现的【您的应用在运行时,未同步告知权限申请的使用目的,向用户索取(存储、拍照)等权限,不符合华为应用市场审核标准。】 使用方式: 1、引入 import permision from "/m…...

【ElasticSearch】概述
文章目录 ElasticSearch1.基本介绍2.设计理念3.基本架构与核心概念学习参考资料: ElasticSearch 简单整理ES基本概念,设计理念,构建与使用,供回顾。 1.基本介绍 Elasticsearch 是一个基于 Apache Lucene 的开源的分布式搜索引擎…...

十进制转十六进制 C/C++蓝桥杯基础试题BASIC-10
问题描述 十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是…...
【LVGL环境搭建】
LVGL环境搭建 win模拟器环境搭建一.二.三.四.五. Ubuntu模拟器环境搭建一. 前置准备二. 下载LVGL Source code:三. 安装sdl2:四. 开启VScode执行五. 安装扩展套件六. 按F5执行七. 执行结果 win模拟器环境搭建 一. 二. 三. 四. 五. Ubuntu模拟器环境…...

【c语言】简单贪吃蛇的实现
目录 一、游戏说明 编辑 二、地图坐标 编辑 三、头文件 四、蛇身和食物 五、数据结构设计 蛇节点结构如下: 封装一个Snake的结构来维护整条贪吃蛇: 蛇的方向,可以一一列举,使用枚举: 游戏状态&a…...

2023年09月CCF-GESP编程能力等级认证Python编程六级真题解析
Python等级认证GESP(1~6级)全部真题・点这里 一、单选题(共15题,共30分) 第1题 近年来,线上授课变得普遍,很多有助于改善教学效果的设备也逐渐流行,其中包括比较常用的手写板,那么它属于哪类设备?( ) A:输入 B:输出 C:控制 D:记录 答案:A 第2题 以下关于…...

Flink中StateBackend(工作状态)与Checkpoint(状态快照)的关系
State Backends 由 Flink 管理的 keyed state 是一种分片的键/值存储,每个 keyed state 的工作副本都保存在负责该键的 taskmanager 本地中。另外,Operator state 也保存在机器节点本地。Flink 定期获取所有状态的快照,并将这些快照复制到持…...
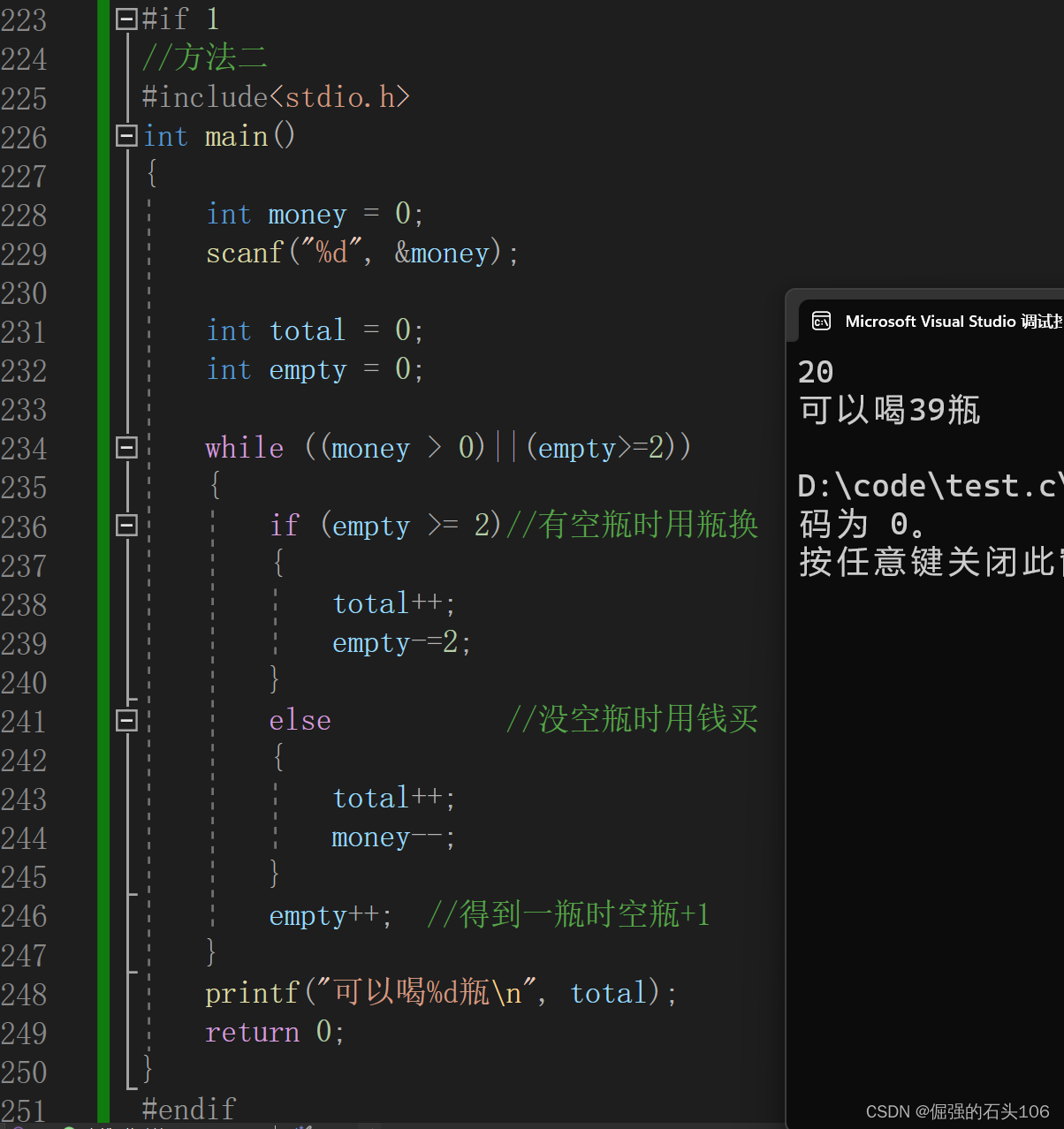
【C语言刷题系列】喝汽水问题
文章目录 一、文章简介 1.先买再换 1.1 代码逻辑: 1.2 完整代码 1.3 运行结果 1.4 根据方法一总结优化 2.边买边换 2.1 代码逻辑: 2.2 完整代码 2.3 运行结果 一、文章简介 本文所述专栏——C语言经典编程问题 C语言刷题_倔强的石头106的博客…...

[C++] C++ 11的functional模块介绍和使用案例
functional模块介绍 functional模块是C 11提供了一组函数对象和算法,用于增强C的函数式编程能力。该模块中的函数对象和算法可以大大简化代码,并提供了一些有用的工具,例如函数适配器和函数对象的组合。 functional模块中的函数对象包括&am…...

kubernetes基本概念和操作
基本概念和操作 1.Namespace1.1概述1.2应用示例 2.Pod2.1概述2.2语法及应用示例 3.Label3.1概述3.2语法及应用示例 4.Deployment4.1概述4.2语法及应用示例 5.Service5.1概述5.2语法及应用示例5.2.1创建集群内部可访问的Service5.2.2创建集群外部可访问的Service5.2.3删除服务5.…...

20240128周报-网络太杂,Tomcat太难
今天来做个小总结吧,之前说想用几个月的时间将Java生态给整理一遍,该工作已经进入第三周了。先和各位老老板汇报一下上一周的工作,然后说一下本周的计划和后面的计划。 1.上周工作 上周的计划是将网络和Tomcat的内容梳理一番,但…...

DES加密原理
DES加密算法综合运用了置换、代替、代数等多种密码技术,具有设计精 巧、实现容易、使用方便等特点。DES加密算法的明文、密文和密钥的分组长度 都是64位,详细的DES加密算法结构如图6-10所示。 图6-10 DES加密算法结构图 DES加密过程如下所示ÿ…...

react 之 useCallback
简单讲述下useCallback的使用方法,useCallback也是用来缓存的,只不过是用于做函数缓存 // useCallbackimport { memo, useCallback, useState } from "react"const Input memo(function Input ({ onChange }) {console.log(子组件重新渲染了…...

OfficeWeb365 Readfile 任意文件读取漏洞复现
0x01 产品简介 OfficeWeb365 是专注于 Office 文档在线预览及PDF文档在线预览云服务,包括 Microsoft Word 文档在线预览、Excel 表格在线预览、Powerpoint 演示文档在线预览,WPS 文字处理、WPS 表格、WPS 演示及 Adobe PDF 文档在线预览。 0x02 漏洞概述 OfficeWeb365 Rea…...
Unity内置的函数)
UnityShader(十三)Unity内置的函数
在计算光照模型时我们需要得到许多数据,比如光源方向、视角方向这种基本信息。 在之前的例子中都是自行在代码里计算的,比如: normalize(_WorldSpaceLight0Pos.xyz) 得到光源方向(这种方法实际只适用平行光) normaliz…...

【开源】基于Qt5的ROS1/ROS2人机交互软件(支持地图编辑/多点导航)
本项目基于Qt5开发,基于CMake进行构建,可以实现一套代码同时在ROS1/ROS2系统中使用(本项目已接入CI,保证多ROS版本/系统版本可用性) 项目地址: https://github.com/chengyangkj/Ros_Qt5_Gui_App 软件在编译时会自动识别环境变量中的ROS1/ROS…...

Spring和SpringBoot的区别是什么
Spring 和 Spring Boot 是 Java 开发领域内两个极其重要且紧密相关的框架,它们各自在企业级应用开发中扮演着不同的角色,并带来了一系列革新性的变化。以下是关于两者之间主要区别的详细分析: 一、设计理念与定位 Spring Framework Spring 是…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...