C#,哥伦布数(Golomb Number)的算法与源代码
1 哥伦布数(Golomb Number)
哥伦布数(Golomb Number)是一个自然数的非减量序列,使得n在序列中正好出现G(n)次。前几个15的G(n)值为:1 2 2 3 3 4 4 4 5 5 5 6 6 6 6
计算结果:

2 源程序,文本格式
using System;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// 哥伦布数(Golomb Number)
/// 哥伦布数(Golomb Number)是一个自然数的非减量序列,使得n在序列中正好出现G(n)次。
/// 前几个15的G(n)值为:1 2 2 3 3 4 4 4 5 5 5 6 6 6 6
/// </summary>
public static partial class Number_Sequence
{
/// <summary>
/// 哥伦布数(Golomb Number)的原始(递归)算法
/// </summary>
/// <param name="n"></param>
/// <returns></returns>
public static int Golomb_Number(int n)
{
if (n == 1)
{
return 1;
}
return 1 + Golomb_Number(n - Golomb_Number(Golomb_Number(n - 1)));
}
/// <summary>
/// 哥伦布数(Golomb Number)的改进(非递归)算法
/// </summary>
/// <param name="n"></param>
/// <returns></returns>
public static int Golomb_Number_Second(int n)
{
int[] dp = new int[n + 1];
dp[1] = 1;
for (int i = 2; i <= n; i++)
{
dp[i] = 1 + dp[i - dp[dp[i - 1]]];
}
return dp[n];
}
}
}
——————————————————————
POWER BY TRUFFER.CN
3 代码格式
using System;namespace Legalsoft.Truffer.Algorithm
{/// <summary>/// 哥伦布数(Golomb Number)/// 哥伦布数(Golomb Number)是一个自然数的非减量序列,使得n在序列中正好出现G(n)次。/// 前几个15的G(n)值为:1 2 2 3 3 4 4 4 5 5 5 6 6 6 6/// </summary>public static partial class Number_Sequence{/// <summary>/// 哥伦布数(Golomb Number)的原始(递归)算法/// </summary>/// <param name="n"></param>/// <returns></returns>public static int Golomb_Number(int n){if (n == 1){return 1;}return 1 + Golomb_Number(n - Golomb_Number(Golomb_Number(n - 1)));}/// <summary>/// 哥伦布数(Golomb Number)的改进(非递归)算法/// </summary>/// <param name="n"></param>/// <returns></returns>public static int Golomb_Number_Second(int n){int[] dp = new int[n + 1];dp[1] = 1;for (int i = 2; i <= n; i++){dp[i] = 1 + dp[i - dp[dp[i - 1]]];}return dp[n];}}
}相关文章:

C#,哥伦布数(Golomb Number)的算法与源代码
1 哥伦布数(Golomb Number) 哥伦布数(Golomb Number)是一个自然数的非减量序列,使得n在序列中正好出现G(n)次。前几个15的G(n)值为:1 2 2 3 3 4 4 4 5 5 5 6…...
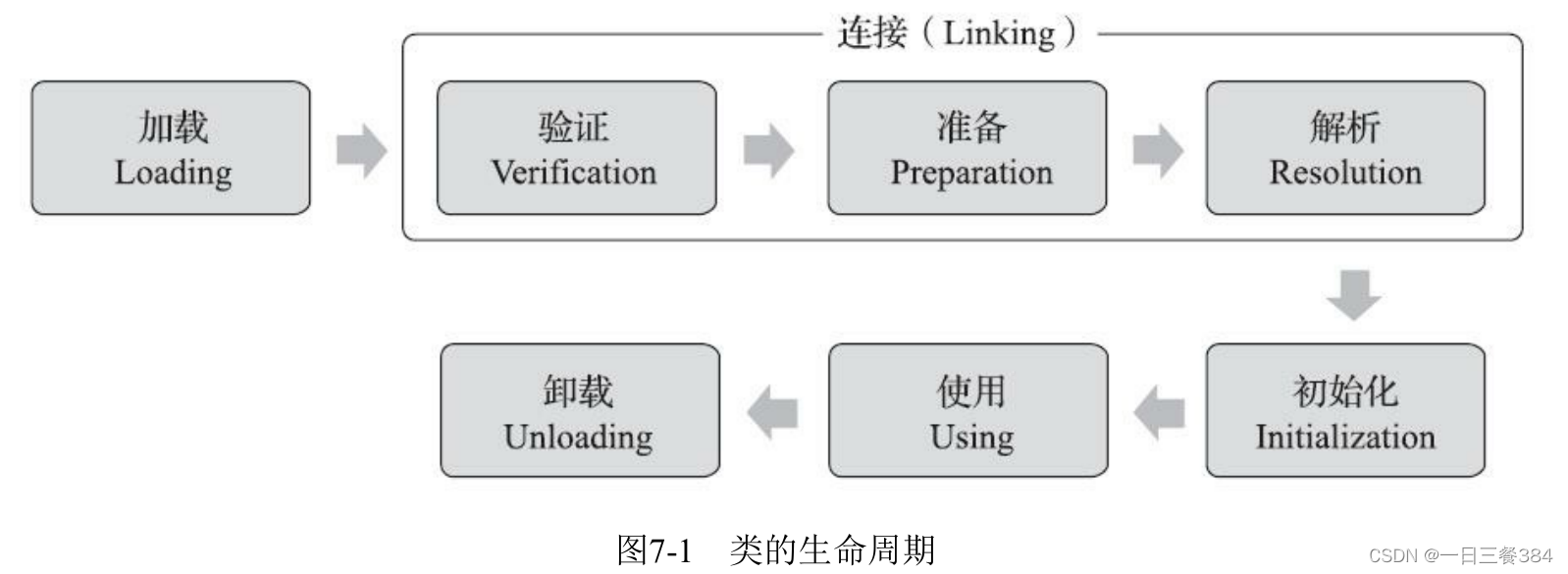
JVM学习
1.Java虚拟机内部有哪些线程共享,那些线程隔离 程序计数器: 通过改变这个计数器的值来选取下一条需要执行的字节码命令 Java虚拟机栈: 栈,每个方法被执行时,Java虚拟机都会同步的创建一个栈帧用于存储局部变量表&…...

Visual Studio 20XX中utf-8中文在控制台显示乱码
文章目录 在 Visual Studio 20xx中,如果源码文件是 UTF8编码,要打印中文到控制台时,控制台会显示乱码,可以进行以下设置。 包含<Windows.h>头文件。在main函数初始调用SetConsoleOutputCP(CP_UTF8)设置控制台输出字符集为UT…...

拥抱个人成长与社会进步:自我认知与开放心态的相互影响
拥抱个人成长与社会进步:自我认知与开放心态的相互影响 Embracing Personal Growth and Societal Progress: The Interplay of Self-Awareness and Open-mindedness 一、引言 I. Introduction 在当今急速发展的时代,个人成长与社会进步交织在一起&…...

【PostgreSQL内核学习(二十五) —— (DBMS存储空间管理)】
DBMS存储空间管理 概述块(或页面)PageHeaderData 结构体HeapTupleHeaderData 结构 表空间表空间的作用:表空间和数据库关系表空间执行案例 补充 —— 模式(Schema) 声明:本文的部分内容参考了他人的文章。在…...
2024年 复习 HTML5+CSS3+移动web 笔记 之CSS遍 第5天
第 五 天 整个网站例 5.1 准备工作 项目目录与版心 base.css 5.2 网页制作思路 5.3 header 区域-整体布局 5.4 header区域-logo 5.5 header区域-导航 index.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8">&l…...

SpringBoot使用Kafka详解含完整代码
1. 前言 随着大数据和实时处理需求的增长,Kafka作为一种分布式流处理平台,与Spring Boot的集成变得尤为重要。本文将详细探讨如何在Spring Boot应用程序中设置和使用Kafka,从基础概念到高级特性,通过实际代码示例帮助读者深入理解…...

解决:java -jar 在cmd中运行 程序卡顿,卡死的 问题。BIO和NIO案例保存
解决 怎么解决,就是 日志别输出到 cmd 就行了。就行了。就行了。 java -jar demo.jar > output.log 2>&1 &最近写东西,遇到了 程序偶尔卡死的情况。是java -jar 启动的。具体卡死为:http请求超级卡顿 或 偶尔反应好多个请求&…...

LeetCode第824题 - 山羊拉丁文
题目 解答 String toGoatLatin(String S) {if (S null) {return "";}S S.trim();if (S.isEmpty()) {return "";}StringBuilder sb new StringBuilder();String[] tokens S.split(" ");for (int i 0, j 1, length tokens.length; i <…...

[Python] 什么是逻辑回归模型?使用scikit-learn中的LogisticRegression来解决乳腺癌数据集上的二分类问题
什么是线性回归和逻辑回归? 线性回归是一种用于解决回归问题的统计模型。它通过建立自变量(或特征)与因变量之间的线性关系来预测连续数值的输出。线性回归的目标是找到一条直线(或超平面),使得预测值与观…...

那些不输于乙游男主人设的国漫男主
最近乙游的势头越来越猛,新宠旧爱一起上阵,叫人应接不暇。在二次元的世界里,乙游男主们凭借着超凡的魅力,成为了无数少女心中的理想对象。他们或冷酷、或温柔、或阳光、或神秘,每一个角色都有着独特的性格和故事。 乙游…...
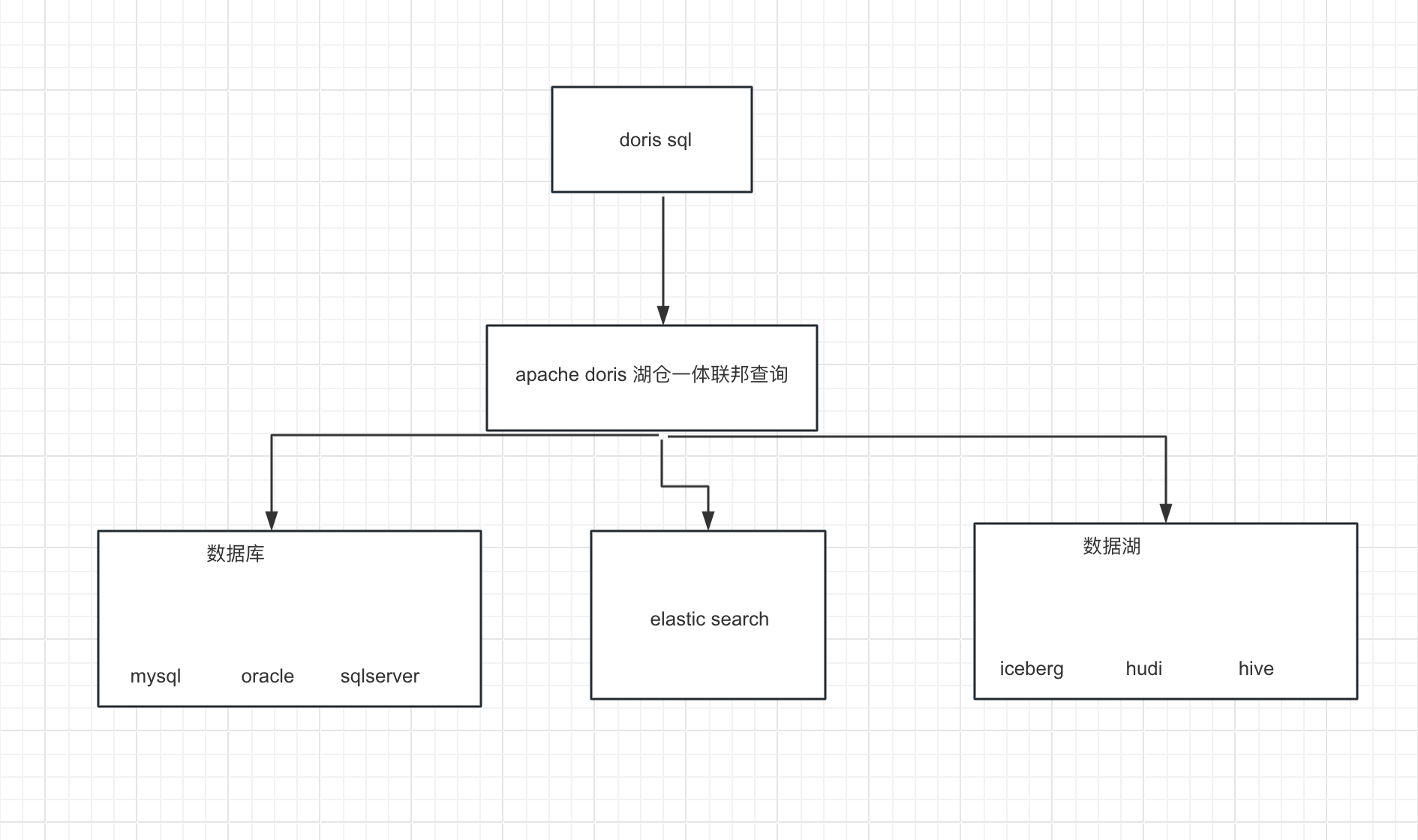
Apache Doris 整合 FLINK CDC + Iceberg 构建实时湖仓一体的联邦查询
1概况 本文展示如何使用 Flink CDC Iceberg Doris 构建实时湖仓一体的联邦查询分析,Doris 1.1版本提供了Iceberg的支持,本文主要展示Doris和Iceberg怎么使用,大家按照步骤可以一步步完成。完整体验整个搭建操作的过程。 2系统架构 我们整…...
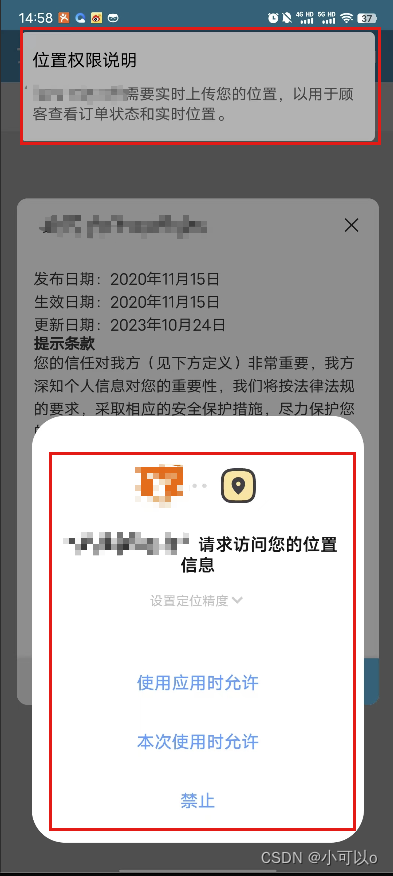
关于华为应用市场上架,申请权限未告知目的被驳回问题的简单处理方式
关于华为应用市场上架过程中出现的【您的应用在运行时,未同步告知权限申请的使用目的,向用户索取(存储、拍照)等权限,不符合华为应用市场审核标准。】 使用方式: 1、引入 import permision from "/m…...

【ElasticSearch】概述
文章目录 ElasticSearch1.基本介绍2.设计理念3.基本架构与核心概念学习参考资料: ElasticSearch 简单整理ES基本概念,设计理念,构建与使用,供回顾。 1.基本介绍 Elasticsearch 是一个基于 Apache Lucene 的开源的分布式搜索引擎…...

十进制转十六进制 C/C++蓝桥杯基础试题BASIC-10
问题描述 十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是…...
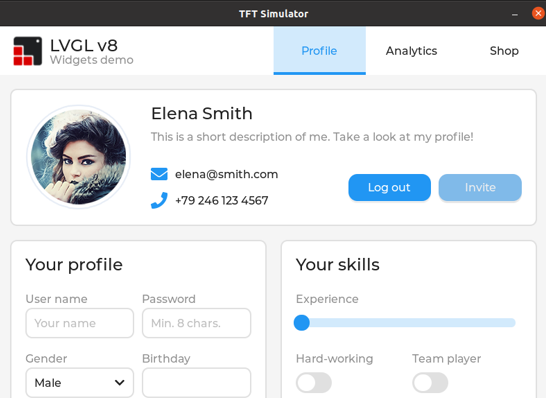
【LVGL环境搭建】
LVGL环境搭建 win模拟器环境搭建一.二.三.四.五. Ubuntu模拟器环境搭建一. 前置准备二. 下载LVGL Source code:三. 安装sdl2:四. 开启VScode执行五. 安装扩展套件六. 按F5执行七. 执行结果 win模拟器环境搭建 一. 二. 三. 四. 五. Ubuntu模拟器环境…...

【c语言】简单贪吃蛇的实现
目录 一、游戏说明 编辑 二、地图坐标 编辑 三、头文件 四、蛇身和食物 五、数据结构设计 蛇节点结构如下: 封装一个Snake的结构来维护整条贪吃蛇: 蛇的方向,可以一一列举,使用枚举: 游戏状态&a…...

2023年09月CCF-GESP编程能力等级认证Python编程六级真题解析
Python等级认证GESP(1~6级)全部真题・点这里 一、单选题(共15题,共30分) 第1题 近年来,线上授课变得普遍,很多有助于改善教学效果的设备也逐渐流行,其中包括比较常用的手写板,那么它属于哪类设备?( ) A:输入 B:输出 C:控制 D:记录 答案:A 第2题 以下关于…...

Flink中StateBackend(工作状态)与Checkpoint(状态快照)的关系
State Backends 由 Flink 管理的 keyed state 是一种分片的键/值存储,每个 keyed state 的工作副本都保存在负责该键的 taskmanager 本地中。另外,Operator state 也保存在机器节点本地。Flink 定期获取所有状态的快照,并将这些快照复制到持…...
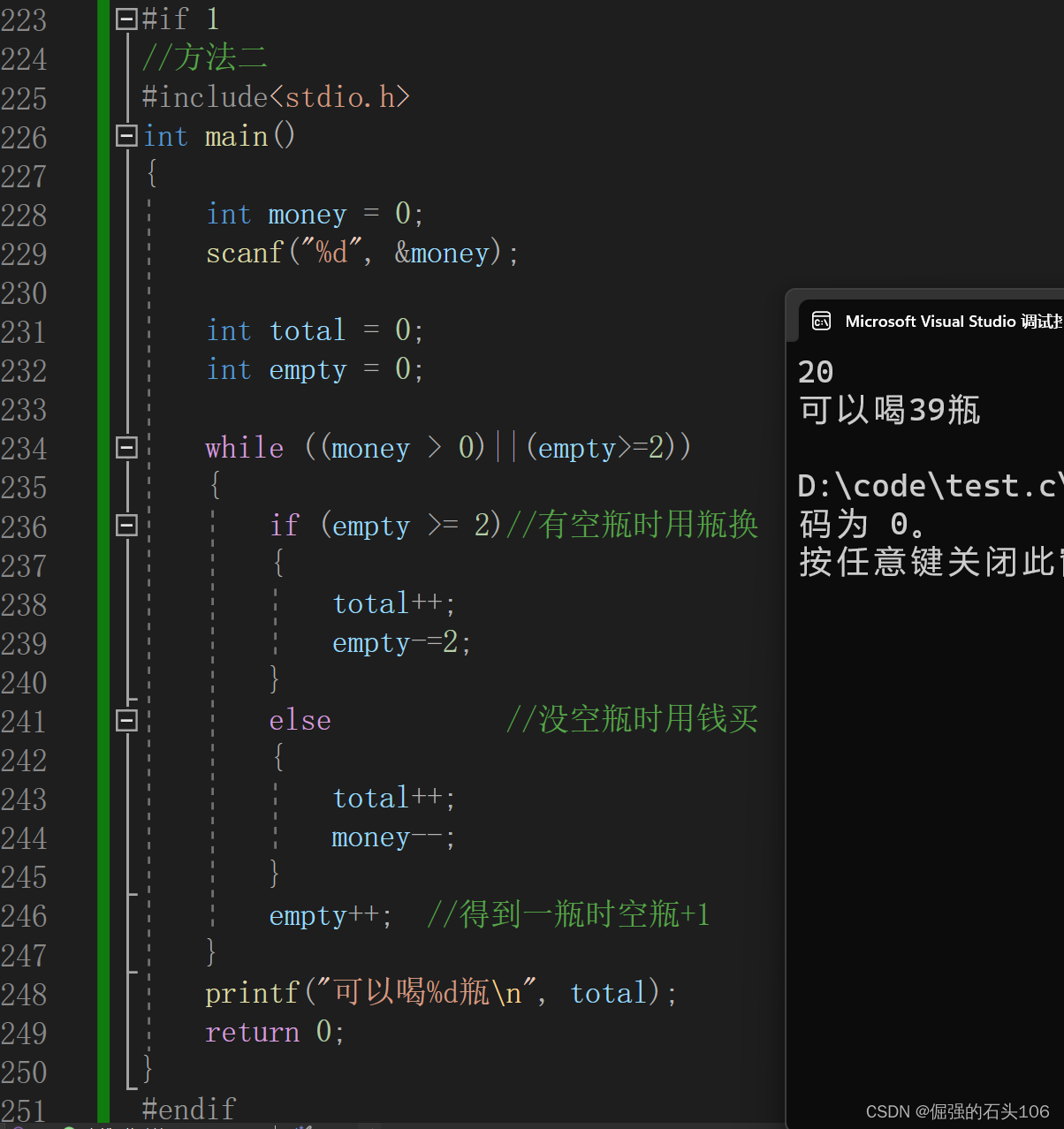
【C语言刷题系列】喝汽水问题
文章目录 一、文章简介 1.先买再换 1.1 代码逻辑: 1.2 完整代码 1.3 运行结果 1.4 根据方法一总结优化 2.边买边换 2.1 代码逻辑: 2.2 完整代码 2.3 运行结果 一、文章简介 本文所述专栏——C语言经典编程问题 C语言刷题_倔强的石头106的博客…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
