【leetcode】完全背包总结
本文内容参考了代码随想录,并进行了自己的总结。
完全背包
关键点
● 每件物品有若干种状态:不选、选 1 件、选 2 件、…、选 n 件
代码
在代码上,只有重量的遍历方向和 01 背包不一样:
for(int i = 0; i < nums.length; i ++ )for(int j = nums[i]; j <= W; j ++ ) {dp[j] = Math.max(dp[j], dp[j - nums[i]);}
正序遍历,意味着每件物品可以选多次,一直往后叠加。
题目
问能装的最大容量,或者问能不能装满的这种题目,属性既是重量又是价值。
下面是代码随想录中,完全背包问题的总结。
| 题目 | 问题转换 | 属性拆解 |
|---|---|---|
| 518. 零钱兑换 II 完全背包 恰好装满,求组合方案数 备注: 组合方案数,就是装的数的顺序不影响结果。比如 3 = 1 + 2 和 3 = 2 + 1 是同一种方案 | 给定背包容量amount,从coins中选若干个物品放入背包,问能装满的组合方案数 | 背包容量:amount。 物品体积:由于是选若干个硬币出来让他们的金额和等于 amount,所以物品的大小(体积)就是硬币金额。 物品价值:这一题没有价值这个维度,只是问背包装满的方案数。 物品数量:每个硬币可以选无数次。 |
| 377. 组合总和 Ⅳ 完全背包 恰好装满,求排列方案数 | 从nums中选若干个数,每个数可重复选择,放入容量为 target的背包,问放满的排列方案数。 | 背包容量:target。 物品体积:由于是选若干个数字出来让他们的和等于 target,所以物品的大小(体积)就是数值大小。 物品价值:这一题没有价值这个维度,只是问背包装满的方案数。 物品数量:每个数字可以选无数次。 |
| https://kamacoder.com/problempage.php?pid=1067 完全背包 恰好装满,求排列方案数 | 从[1, m]中,选若干个数,每个数可选无数次,放入大小为n的背包,问放满的排列方案数 | 背包容量:n。 物品体积:由于是选若干个数字出来让他们的和等于 n,所以物品的大小(体积)就是数值大小。 物品价值:这一题没有价值这个维度,只是问背包装满的方案数。 物品数量:每个数字可以选无数次。 |
| 322. 零钱兑换 完全背包 恰好装满,求最小价值 | 给定n个数,选若干个数,每个数无限取,求能放满背包的最少数的个数。 给定n个数,选若干个数,每个数无限取,求恰好装满时,最小价值为多少? | 背包容量:n。 物品体积:由于是选若干个数字出来让他们的和等于 n,所以物品的大小(体积)就是数值大小。 由于是求最少数的个数,所以每个数的价值就是 1。 物品数量:每个数字可以选无数次。 |
| 279. 完全平方数 完全背包 恰好装满,求最小价值 | 从[1, sqrt(n)]中选若干个数,每个数可选无数次,将其平方放入大小为n的背包中,求能放满的最少数量 从[1, sqrt(n)]中选若干个数,每个数可选无数次,将其平方放入大小为n的背包中,求恰好装满时,最小价值为多少? | 背包容量:n。 物品体积:由于是选若干个数字出来让他们平方的和等于 n,所以物品的大小(体积)就是数值大小。 物品价值:由于是求最少数的个数,所以每个数的价值就是 1 物品数量:每个数字可以选无数次。 |
| 139. 单词拆分 完全背包 按顺序恰好装满,求是否存在方案 | 从n个字符串中选若干个字符串,每个字符串可重复使用,拼成长度为s.length()的字符串,问是否能拼成? 从n个物品中选若干个物品,每个物品可重复使用,放入大小为s.length()的背包,问是否能装满? 这n个物品是有顺序的,即必须按照一定的顺序拼成字符串s,所以求的是是否存在一种排列能够拼成字符串s,所以遍历顺序应该先遍历长度 | 背包容量:s.length()。 物品体积:由于是选若干个字符串出来让他们的长度等于 n,所以物品的大小(体积)就是数值大小。 物品价值:这一题没有价值这个维度,只是问背包装满是否存在方案。 物品数量:每个字符串可以选无数次。 |
- 单词拆分其实是的377. 组合总和 Ⅳ的子问题。
相同点:
- 每个字符串相当于每个数字,都是物品
- 每个字符串的长度相当于每个数字的数值大小,都是物品的大小
不同点:
-
- 单词拆分问题问的是,是否存在一种特定的排列能装满背包?这个特定的排列装满背包,就是指按照顺序拼接字符串。而给定的字符串 s 就表明了,字符串一定要按照这个顺序拼接
-
- 组合总和 Ⅳ问题问的是,能装满背包有多少种不同的排列方案,即任意一种放入的顺序都算一种方案
相关文章:

【leetcode】完全背包总结
本文内容参考了代码随想录,并进行了自己的总结。 完全背包 关键点 ● 每件物品有若干种状态:不选、选 1 件、选 2 件、…、选 n 件 代码 在代码上,只有重量的遍历方向和 01 背包不一样: for(int i 0; i < nums.length; i…...
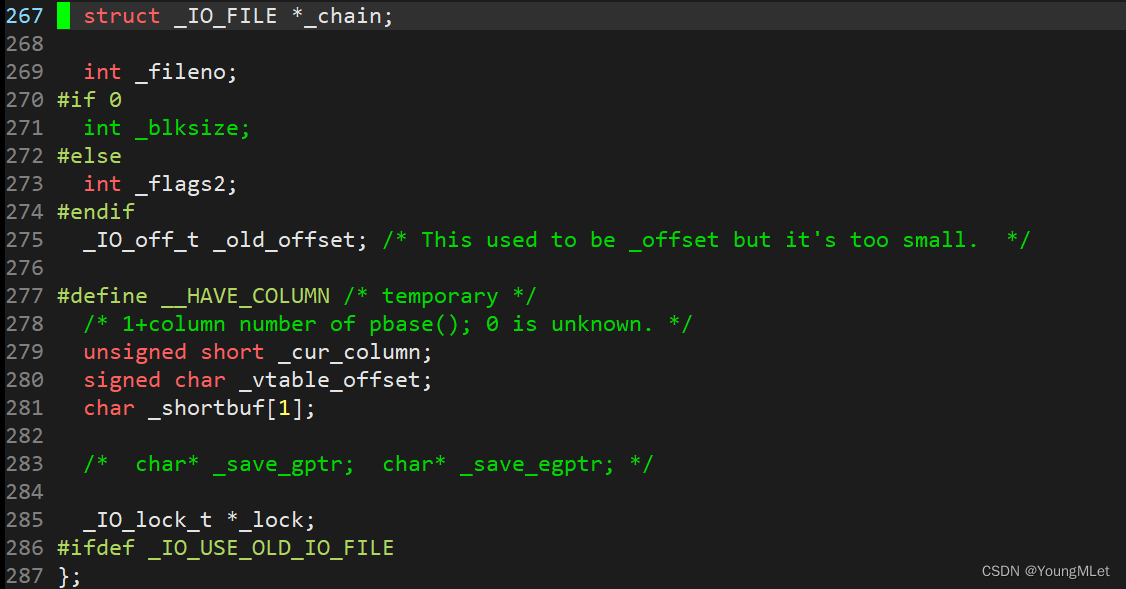
【Linux】理解系统中一个被打开的文件
文件系统 前言一、C语言文件接口二、系统文件接口三、文件描述符四、struct file 对象五、stdin、stdout、stderr六、文件描述符的分配规则七、重定向1. 重定向的原理2. dup23. 重谈 stderr 八、缓冲区1. 缓冲区基础2. 深入理解缓冲区3. 用户缓冲区和内核缓冲区4. FILE 前言 首…...
k8s kubeadm部署安装详解
目录 kubeadm部署流程简述 环境准备 步骤简述 关闭 防火墙规则、selinux、swap交换 修改主机名 配置节点之间的主机名解析 调整内核参数 所有节点安装docker 安装依赖组件 配置Docker 所有节点安装kubeadm,kubelet和kubectl 定义kubernetes源并指定版本…...

RT-DETR算法优化改进: 下采样系列 | 一种新颖的基于 Haar 小波的下采样HWD,有效涨点系列
💡💡💡本文独家改进:HWD的核心思想是应用Haar小波变换来降低特征图的空间分辨率,同时保留尽可能多的信息,与传统的下采样方法相比,有效降低信息不确定性。 💡💡💡使用方法:代替原始网络的conv,下采样过程中尽可能包括更多信息,从而提升检测精度。 RT-DET…...

CocosCreator3.8源码分析
Cocos Creator架构 Cocos Creator 拥有两套引擎内核,C 内核 和 TypeScript 内核。C 内核用于原生平台,TypeScript 内核用于 Web 和小游戏平台。 在引擎内核之上,是用 TypeScript 编写的引擎框架层,用以统一两套内核的差异…...
(已解决)spingboot 后端发送QQ邮箱验证码
打开QQ邮箱pop3请求服务:(按照QQ邮箱引导操作) 导入依赖(不是maven项目就自己添加jar包): <!-- 邮件发送--><dependency><groupId>org.springframework.boot</groupId><…...

【蓝桥杯冲冲冲】[NOIP2001 普及组] 装箱问题
蓝桥杯备赛 | 洛谷做题打卡day26 文章目录 蓝桥杯备赛 | 洛谷做题打卡day26题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示思路 题解代码我的一些话 [NOIP2001 普及组] 装箱问题 题目描述 有一个箱子容量为 V V V,同时有 n n n 个物品,每…...

2024牛客寒假算法基础集训营1
文章目录 A DFS搜索M牛客老粉才知道的秘密G why外卖E 本题又主要考察了贪心B 关鸡C 按闹分配 今天的牛客,说是都是基础题,头昏昏的,感觉真不会写,只能赛后补题了 A DFS搜索 写的时候刚开始以为还是比较难的,和dfs有关…...

元素的显示与隐藏,精灵图,字体图标,CSSC三角
元素的显示与隐藏 类似网站广告,当我们点击关闭就不见了,但是我们重新刷新页面,会重新出现 本质:让元素在页面中隐藏或者显示出来。 1.display显示隐藏 2.visibility显示隐藏 3.overflow溢出显示隐藏 1.display属性(…...

最新!2024顶级SCI优化!TTAO-CNN-BiGRU-MSA三角拓扑聚合优化、双向GRU融合注意力的多变量回归预测程序!
适用平台:Matlab 2023版及以上 TTOA三角聚合优化算法,将在2024年3月正式发表在中科院1区顶级SCI期刊《Expert Systems with Applications》上。 该算法提出时间极短,目前以及近期内不会有套用这个算法的文献。新年伊始,尽快拿下…...
)
Flink SQL Client 安装各类 Connector、组件的方法汇总(持续更新中....)
一般来说,在 Flink SQL Client 中使用各种 Connector 只需要该 Connector 及其依赖 Jar 包部署到 ${FLINK_HOME}/lib 下即可。但是对于某些特定的平台,如果 AWS EMR、Cloudera CDP 等产品会有所不同,主要是它们中的某些 Jar 包可能被改写过&a…...
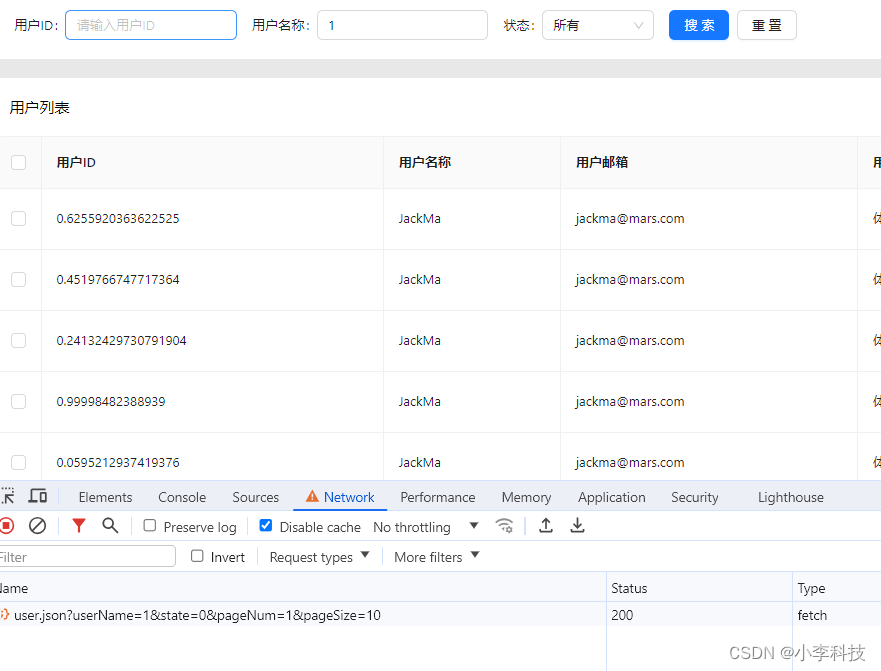
React18-模拟列表数据实现基础表格功能
文章目录 分页功能分页组件有两种接口参数分页类型用户列表参数类型 模拟列表数据分页触发方式实现目录 分页功能 分页组件有两种 table组件自带分页 <TableborderedrowKey"userId"rowSelection{{ type: checkbox }}pagination{{position: [bottomRight],pageSi…...

MySQL查询数据(十)
MySQL查询数据(十) 一、SELECT基本查询 1.1 SELECT语句的功能 SELECT 语句从数据库中返回信息。使用一个 SELECT 语句,可以做下面的事: **列选择:**能够使用 SELECT 语句的列选择功能选择表中的列,这些…...
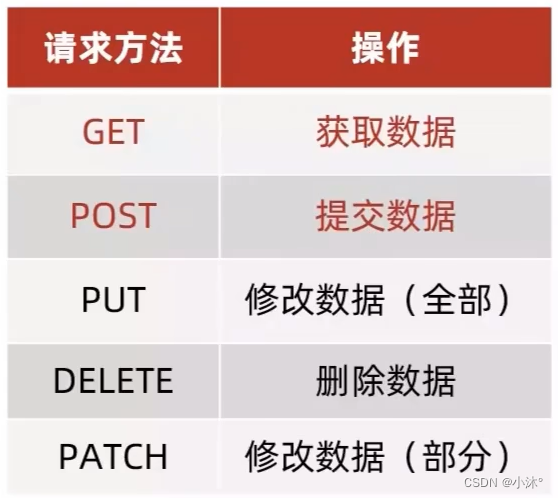
AJAX-常用请求方法和数据提交
常用请求方法 请求方法:对服务器资源,要执行的操作 axios请求配置 url:请求的URL网址 method:请求的方法,如果是GET可以省略;不用区分大小写 data:提交数据 axios({url:目标资源地址,method…...
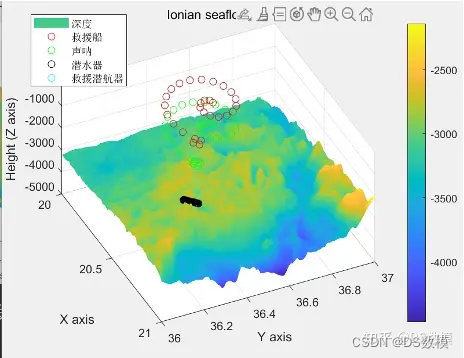
2024美国大学生数学建模竞赛美赛B题matlab代码解析
2024美赛B题Searching for Submersibles搜索潜水器 因为一些不可抗力,下面仅展示部分代码(很少部分部分)和部分分析过程,其余代码看文末 Dthxlsread(C:\Users\Lenovo\Desktop\Ionian.xlsx); DpDth(:,3:5); dy0.0042; dx0.0042; …...

【DouYing Desktop】
I) JD 全日制大专及以上学历; 2. 3年以上的IT服务支持相关工作经验 3. 有较强的桌面相关trouble shooting与故障解决能力,能够独立应对各类型桌面问题; 4. 具备基础的网络、系统知识,能够独立解决常见的网络、系统等问题…...
正则表达式与文本处理工具
目录 引言 一、正则表达式基础 (一)字符匹配 1.基本字符 2.特殊字符 3.量词 4.边界匹配 (二)进阶用法 1.组与引用 2.选择 二、命令之-----grep (一)基础用法 (二)高级用…...
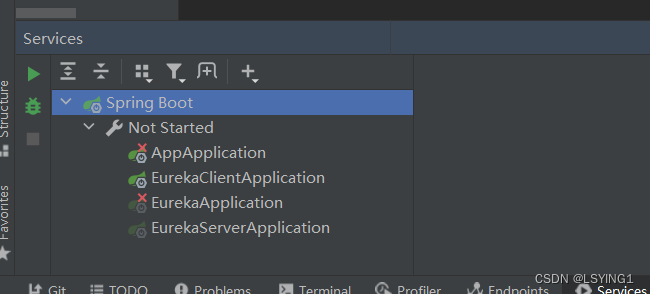
IDEA中的Run Dashboard
Run Dashboard是IntelliJ IDEA中的工具【也就是View中的Services】,提供一个可视化界面,用于管理控制应用程序的运行和调试过程。 在Run DashBoard中,可以看到所有的运行配置,以及每个配置的运行状态(正在运行…...

【力扣白嫖日记】SQL
前言 练习sql语句,所有题目来自于力扣(https://leetcode.cn/problemset/database/)的免费数据库练习题。 今日题目: 1407.排名靠前的旅行者 表:Users 列名类型idintnamevarchar id 是该表中具有唯一值的列。name …...
)
自动化报告pptx-python|高效通过PPT模版制造报告(三)
这是自动化报告学习的第三篇了,前面两篇分别是: 自动化报告的前奏|使用python-pptx操作PPT(一)自动化报告pptx-python|如何将pandas的表格写入PPTX(二)本篇是逼着笔者看到JoStudio 大佬自己写的一个jojo-office 库,基于pptx-python开发成一套试用office软件的依赖,非…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
