大数据信用报告查询费用一般要多少钱?
一些不少朋友在申贷的时候被拒贷之后,得到的原因就是因为大数据不良被拒,这时候很多人都反过来查询自己的大数据信用报告,而查询的价格也是不少朋友都比较关注的,那大数据信用报告查询费用一般要多少钱呢?下面本文就为你介绍一下。
大数据信用查询受以下两点影响:

一、大数据信用查询费用受渠道影响
一些渠道的由于查询成本的原因,价格普遍定的比较高,特别是一些金融中介公司的查询,由于是定向为客户查询,报价也是比较高的,还有的是代查的方式,费用更是由中介公司乱报,一般及时到几百不等。
二、大数据信用查询费用受服务影响
一些大数据信用查询平台,由于提供的服务不一样,查询的价格不一样。有的大数据信用查询平台不会提供任何的售后服务,这样的查询平台的查询费用就便宜一些,有的平台,提供报告解读服务的,像小易大数据的价格就比不提供任何售后的平台稍微贵一点,一般在40-50元之间。

大数据查询要注意什么?
大数据信用查询首先要注意选择合适的平台和适合自己的大数据信用报告版本。由于版本不一样,查询的结果也就不一样,同时也需要选择有固定网站的大数据信用查询平台。
大数据信用报告查询平台选哪个好?
大数据信用查询的平台有很多,小易大数据平台是市面上唯一一个提供大数据报告解读服务的平台,多年的解读服务深的用户的信赖和选择。

上述就是关于大数据信用报告查询费用一般要多少钱的全部介绍,如果你正想了解自己的大数据信用情况,希望本问的介绍对你有一定的帮助。
相关文章:

大数据信用报告查询费用一般要多少钱?
一些不少朋友在申贷的时候被拒贷之后,得到的原因就是因为大数据不良被拒,这时候很多人都反过来查询自己的大数据信用报告,而查询的价格也是不少朋友都比较关注的,那大数据信用报告查询费用一般要多少钱呢?下面本文就为你介绍一下…...
【操作宝典】IntelliJ IDEA新建maven项目详细教程
目录 🌼1. 配置maven环境 🌼2. 创建maven项目 🌼3. 创建maven项目完整示例 a. 导入spring boot环境 b. 修改maven配置 c. 下载jar包 d. 创建Java类 🌼1. 配置maven环境 【安装指南】maven下载、安装与配置详细教程-CSDN博客…...

【Java程序设计】【C00196】基于(JavaWeb+SSM)的旅游管理系统(论文+PPT)
基于(JavaWebSSM)的旅游管理系统(论文PPT) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于ssm的旅游平台 本系统分为前台、管理员2个功能模块。 前台:当游客打开系统的网址后,首先看到的…...
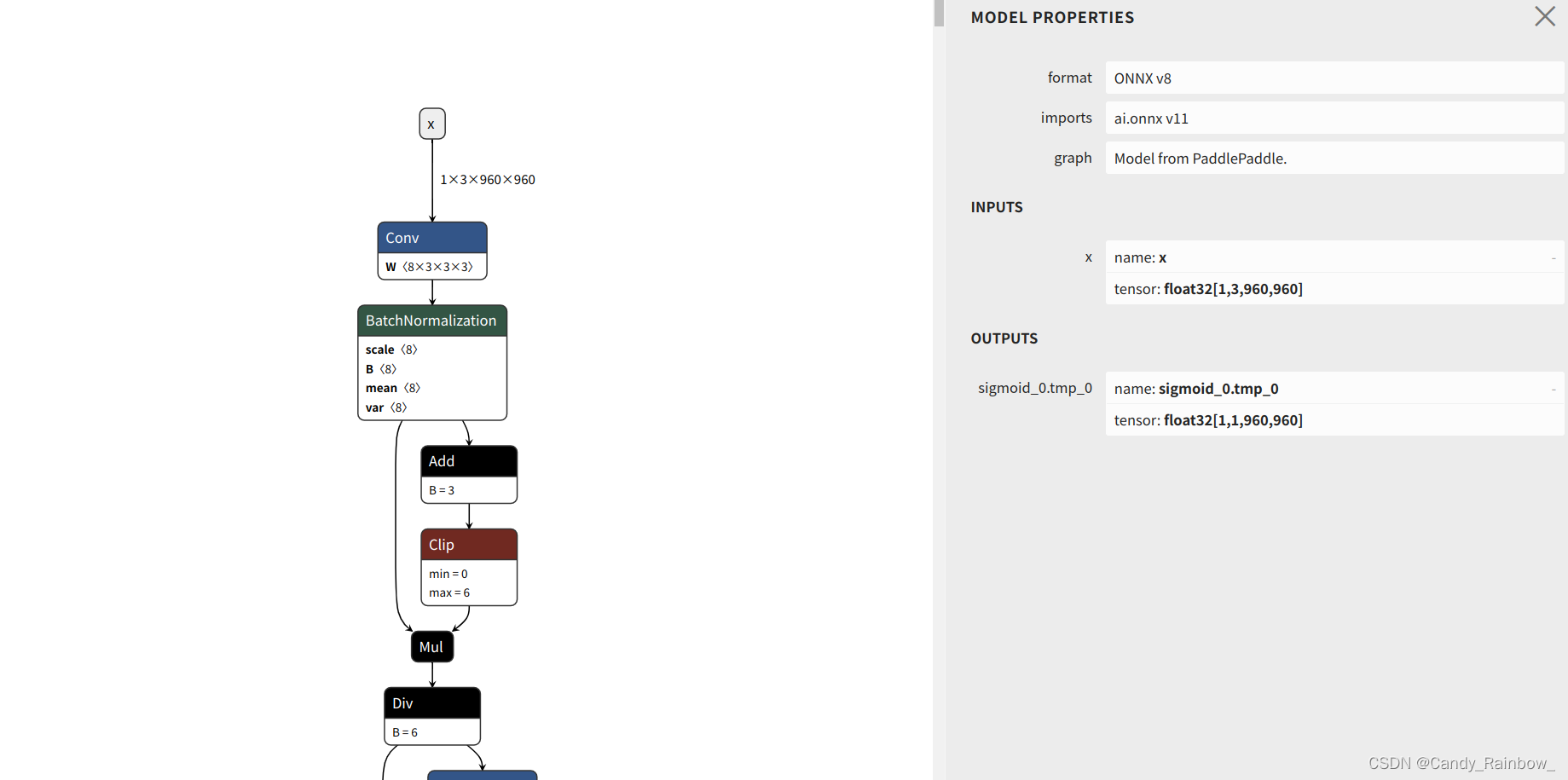
pdmodel从动态模型转成静态onnx
1.下载项目 git clone https://github.com/jiangjiajun/PaddleUtils.git 2.新建两个新的文件夹 第一个文件夹放两个必要文件 第二个文件夹可以设置为空,用来存放转换后的模型 如图: 3.在终端运行 python paddle/paddle_infer_shape.py --model_dir …...
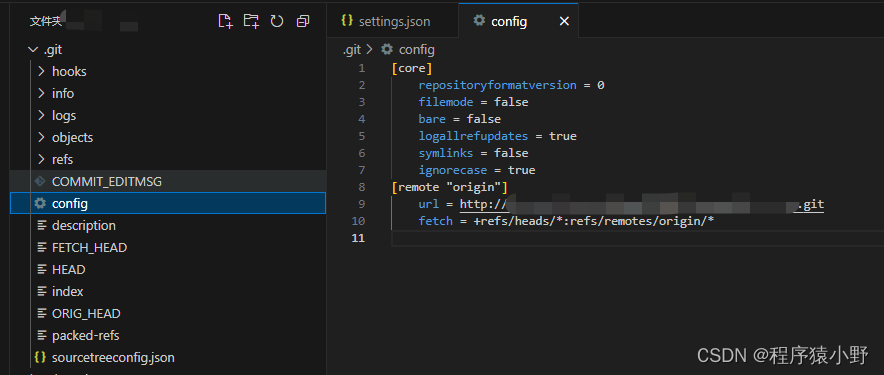
git 如何修改仓库地址
问题背景:组内更换大部门之后,代码仓的地址也迁移了,所以原来的git仓库地址失效了。 虽然重新建一个新的文件夹,再把每个项目都git clone一遍也可以。但是有点繁琐,而且有的项目本地还有已经开发一半的代码,…...
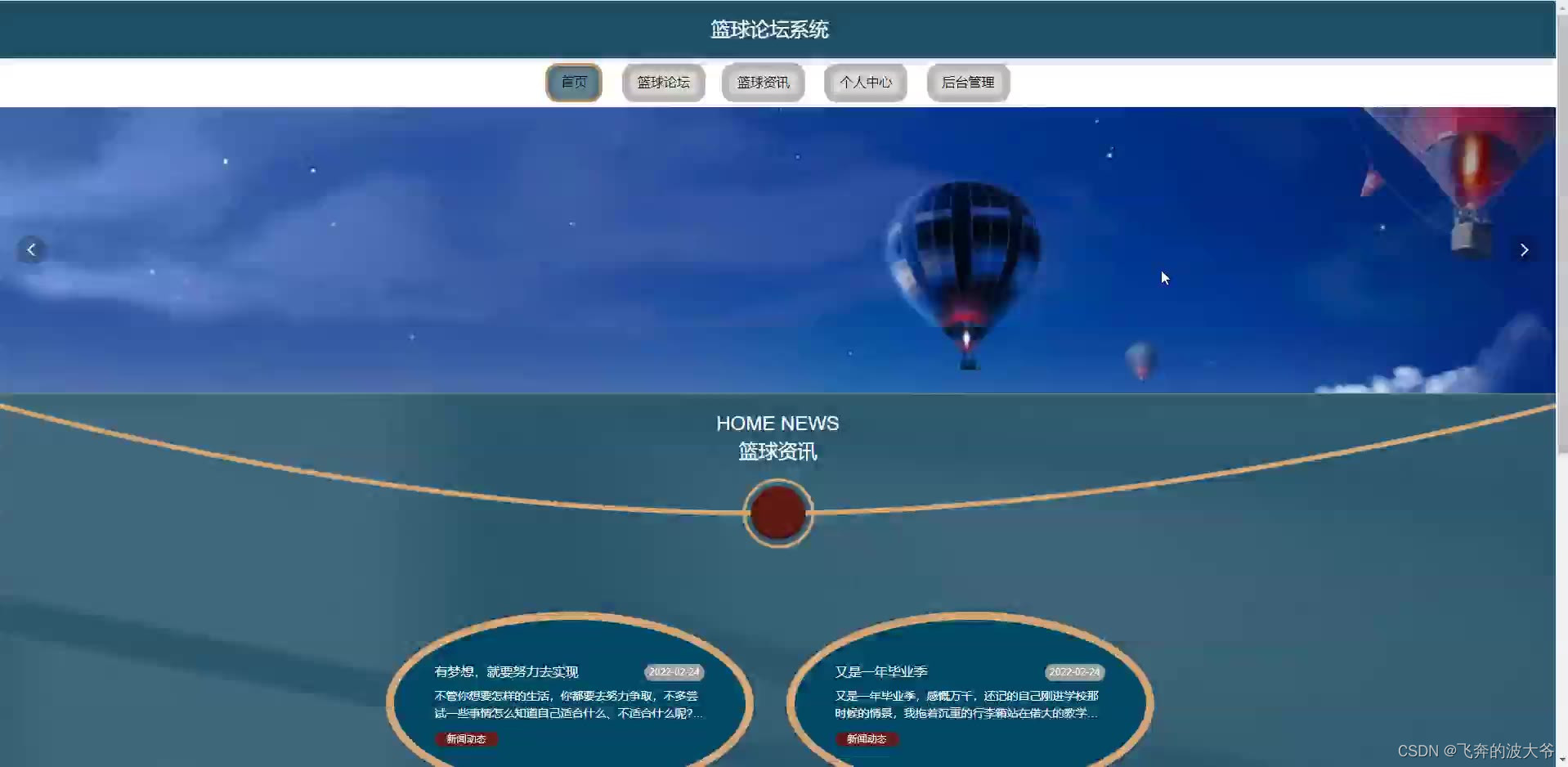
基于springboot篮球论坛系统源码和论文
首先,论文一开始便是清楚的论述了系统的研究内容。其次,剖析系统需求分析,弄明白“做什么”,分析包括业务分析和业务流程的分析以及用例分析,更进一步明确系统的需求。然后在明白了系统的需求基础上需要进一步地设计系统,主要包罗软件架构模式、整体功能模块、数据库设计。本项…...

【三维重建】运动恢复结构(SfM)
运动恢复结构是通过三维场景的多张图像,恢复出该场景的三维结构信息以及每张图片对应的摄像机参数。 欧式结构恢复(内参已知,外参未知) 欧式结构恢复问题: 已知:1、n个三维点在m张图像中的对应点的像素坐标 2、相机内参 求解&…...
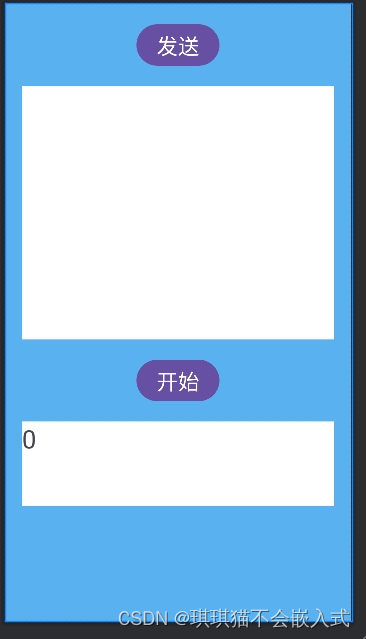
Android Studio非UI线程修改控件——定时器软件
目录 一、UI界面设计 1、UI样式 2、XML代码 二、功能编写 1、定义 2、实现方法 3、功能实现 一、UI界面设计 1、UI样式 2、XML代码 <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android…...

canvas的一些基础
在 Canvas 中,基本图形有两种:直线图形和曲线图形 直线图形:直线、矩形(描边矩形和填充矩形)、多边形 曲线图形:曲线和弧线(弧线是圆的一部分,曲线则不一定,弧线上的每个点都具有相同的曲率&…...

C++(10)——类与对象(最终篇)
目录 static成员 概念 特性 友元 友元函数 友元类 内部类 匿名对象 经过这么多天的分享,C的类与对象终于要结束了。结束也意味着C快要入门了。 static成员 概念 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之…...

NetApp FAS2750 和 FAS2820 简化分布式企业的存储
拥有分布式企业和多个办公位置的客户希望使用这些系统进行虚拟化,以及为大型 FAS 和 AFF 系统提供简单且经济高效的备份和灾难恢复。 NetApp FAS2750 的规格 非常适合需要轻松部署和简化运维的中小型企业。 • 每个 HA 对的最大原始容量:1.2 PB • 每个…...
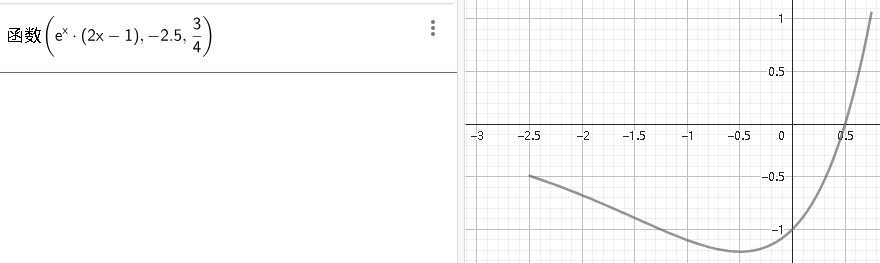
Geogebra设置函数定义域
曲线方程设置范围 y 4x 0 / (-4 < y < 4) 函数设置范围 函数(e^x*(2x-1),-2.5,3/4)...
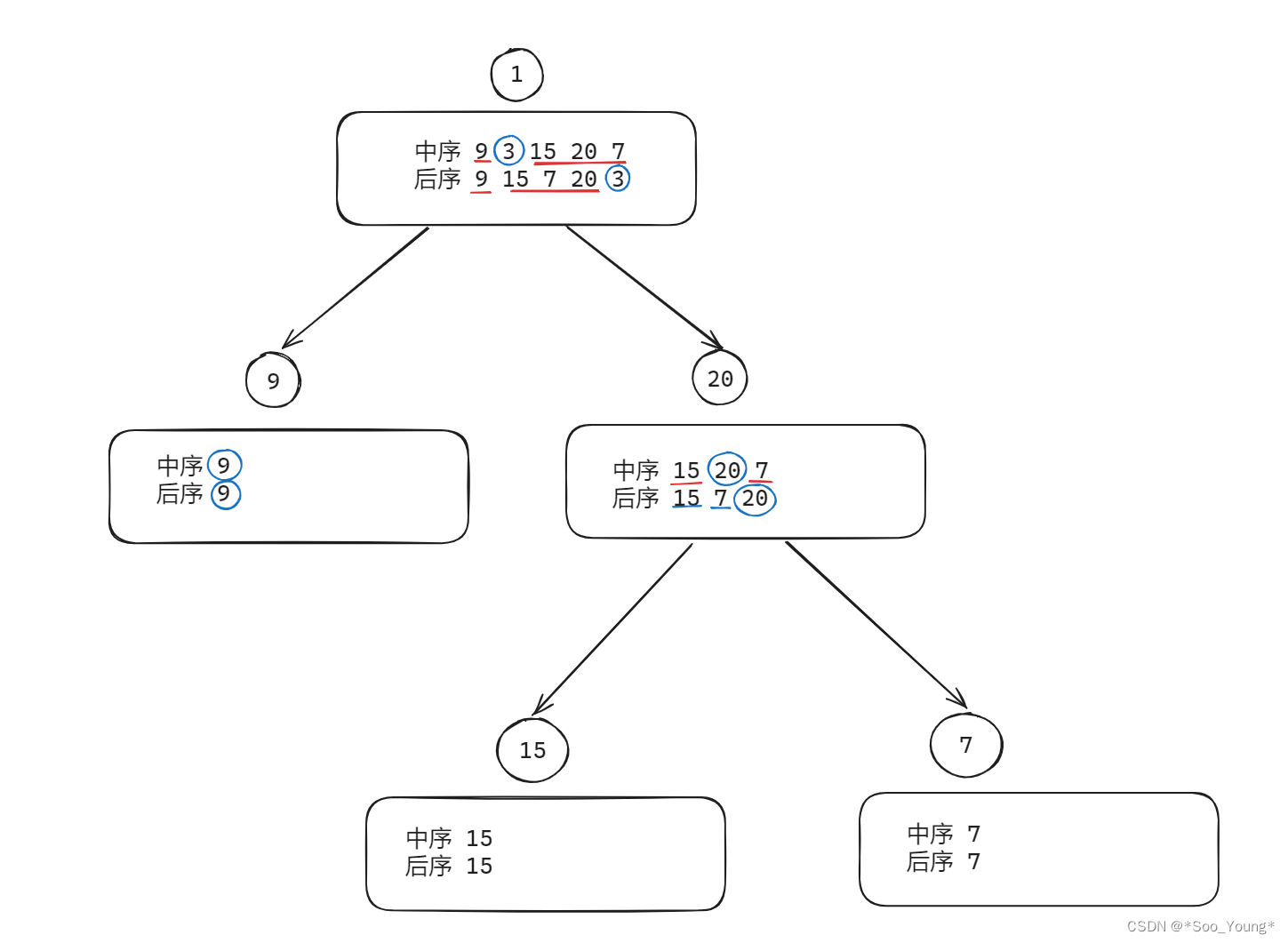
代码随想录刷题笔记 DAY 18 | 找树左下角的值 No.513 | 路经总和 No.112 | 从中序与后序遍历序列构造二叉树 No.106
Day 18 01. 找树左下角的值(No. 513) 题目链接 代码随想录题解 1.1 题目 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 示例 1: 输入: root [2,1,3] 输出: 1 示例 2: 输入…...
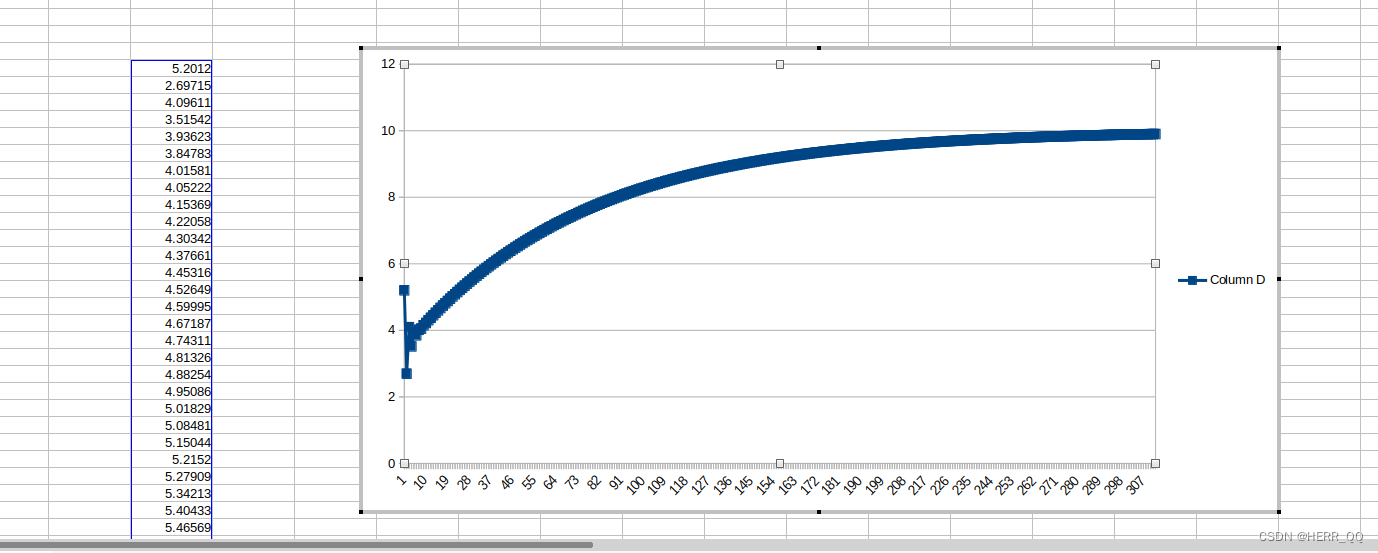
【algorithm】一个简单的PID工程 base 用于手生时候快速复习 用于设计模式 cpp语法八股 快速复习校验
写在前面 最近项目一直用matlab,防止手生整一个回忆工具使用的简单的pid demo,走一边流程,包括配工程debug看结果,复用之前记录的配置见我的bloghttps://blog.csdn.net/weixin_46479223/article/details/135082867?csdn_share_t…...

Python处理图片生成天际线(2024.1.29)
1、天际线简介 天际线(SkyLine)顾名思义就是天空与地面的边界线,人站在不同的高度,会看到不同的景色和地平线,天空与地面建筑物分离的标记线,不得不说,每天抬头仰望天空,相信大家都可…...

jsp服装穿搭推荐系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP 游戏网上商城系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0…...
Opencv(C++)学习 之RV1126平台的OPENCV交叉编译
本文特点:网上已经有了很多opencv移植RV1106的文章,本文主要记录基于cmake-gui编译,碰到的报错,及解决报错问题的方法,同时简单总结一些配置项相关的知识。 一、环境: ubuntu18 x64 RV1126交叉编译工具链 …...

http和https区别
HTTP协议以明文方式发送内容,不提供任何方式的数据加密。HTTP协议不适合传输一些敏感信息,比如:信用卡号、密码等支付信息。https则是具有安全性的ssl加密传输协议。http和https使用的是完全不同的连接方式,用的端口也不一样&…...
富文本编辑器CKEditor4简单使用-05(开发自定义插件入门)
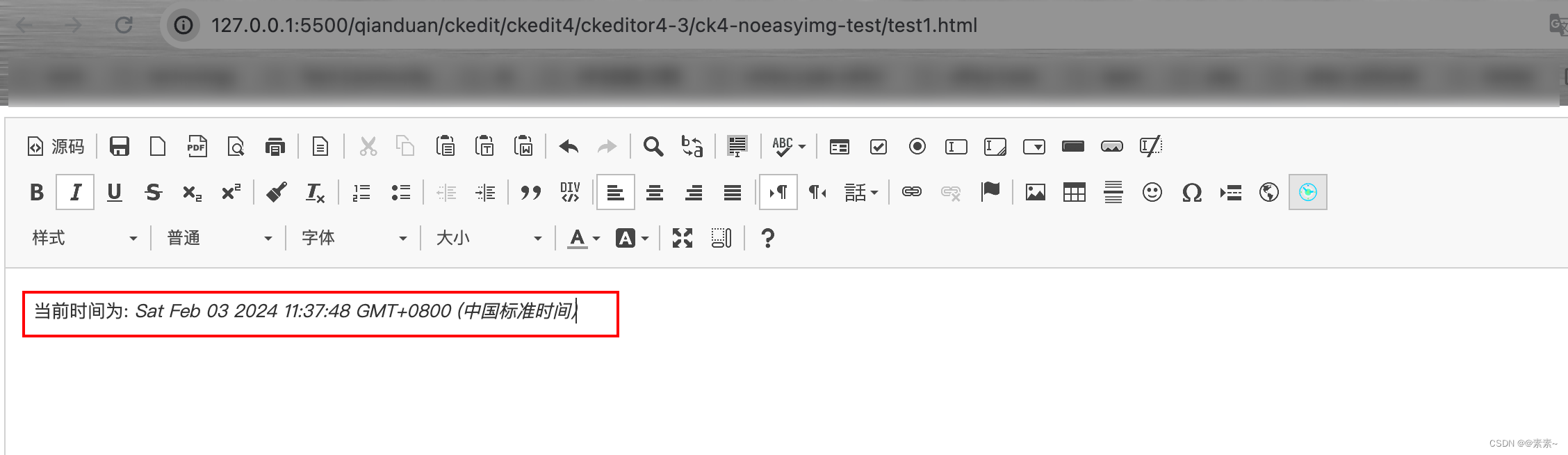
富文本编辑器CKEditor4简单使用-05(开发自定义插件入门) 1. CKEditor4插件入门1.1 关于CKEditor4插件的简单安装与使用1.2 参考 2. 开发自定义插件——当前时间插件2.1 创建插件文件目录结构2.2 编写插件原代码2.2.1 编写代码框架2.2.2 创建编辑器命令2.…...

chisel之scala 语法
Chisel新手教程之Scala语言(1) Value & variable Value是immutable的,当它被分配一个数据后,无法进行重新分配。用 val 表示。 Variable是mutable的,可以重复赋值。用 var 表示。示例如下: val a …...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
