LeetCode.1686. 石子游戏 VI
题目
题目链接
分析
本题采取贪心的策略
我们先假设只有两个石头a,b,
对于 Alice 价值分别为 a1,a2,
对于 Bob 价值而言价值分别是 b1,b2
- 第一种方案是 Alice取第一个,Bob 取第二个,Alice与Bob的价值差是 c1 = a1 - b1;
- 第一种方案是 Alice取第二个,Bob 取第一个,Alice与Bob的价值差是 c1 = a2 - b2;
那么这两种方案对于 Alice来说哪一种更优呢??
取决于两种方案的价值差,记 c = c1 - c2 = (a1 - b2) - (a2 - b1) = (a1 + b1) - (a2 + b2);
如果 c > 0,那么方案一更优,如果 c == 0,则两种方案一样,如果 c < 0,则方案二更优。
那么比较两个方案的优劣其实就是比较 a1+b1 与 a2+b2 的优劣,也就是比较每个下标i的a[i]+b[i]的优劣。
所以贪心的策略:将两组石头的价值合并,每次取价值最大的那一组。
总结以上:先将两个数组的价值合并,并用下标去标记,对价值进行排序,
Alice取偶数下标,Bob取奇数下标,最后比较Alice和Bob的价值总和。
代码
class Solution {public int stoneGameVI(int[] aliceValues, int[] bobValues) {int n = aliceValues.length;Integer[] ids = new Integer[n];for (int i = 0; i < n; ++i) ids[i] = i;// 两个数组价值之和按照 大->小 排序,ids 记录下标// 例如: aliceValues = {1, 2, 3}; bobValues = {3, 1, 3};// 经过下面的代码:ids = {2,0,1}Arrays.sort(ids, (a, b) -> {int val1 = aliceValues[a] + bobValues[a];int val2 = aliceValues[b] + bobValues[b];return val2 - val1;});// Alice 价值总和int alisCount = 0;// Bob 价值总和int bobCount = 0;for(int i =0;i < n;i ++) {// 偶数下标,Alice取值if(i % 2 == 0) {alisCount += aliceValues[ids[i]];}else {// 奇数下标,Bob取值bobCount += bobValues[ids[i]];}}if(alisCount - bobCount > 0) {return 1;}else if(alisCount == bobCount) {return 0;}else {return -1;}}
}
相关文章:

LeetCode.1686. 石子游戏 VI
题目 题目链接 分析 本题采取贪心的策略 我们先假设只有两个石头a,b, 对于 Alice 价值分别为 a1,a2, 对于 Bob 价值而言价值分别是 b1,b2 第一种方案是 Alice取第一个,Bob 取第二个,Alice与Bob的价值差是 c1 a1 - b1…...

【硬件产品经理】锂电池充电时间怎么计算?
目录 前言 电池容量 充电器功率 电能转换效率 充电时间计算 作者简介<...

Oracle篇—普通表迁移到分区表(第五篇,总共五篇)
☘️博主介绍☘️: ✨又是一天没白过,我是奈斯,DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux,也在积极的扩展IT方向的其他知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章,并且也会默默的点赞收藏加关注❣…...

作为开发人的我们,怎么可以不了解这些?
必备技能: 文章结尾处,有资源获取方式 Spring Spring是一个轻量级的Java框架,它可以用于开发各种Java应用程序。Spring提供了丰富的功能,包括IoC容器、AOP、事务管理、Web开发、安全管理等等。Spring的IoC容器可以…...

基于 Echarts 的 Python 图表库:Pyecahrts交互式的日历图和3D柱状图
文章目录 概述一、日历图和柱状图介绍1. 日历图基本概述2. 日历图使用场景3. 柱状图基本概述4. 柱状图使用场景 二、代码实例1. Pyecharts绘制日历图2. Pyecharts绘制2D柱状图3. Pyecharts绘制3D柱状图 总结 概述 本文将引领读者深入了解数据可视化领域中的两个强大工具&#…...
web应用课——(第四讲:中期项目——拳皇)
代码AC Git地址:拳皇——AC Git链接...
Python爬虫http基本原理
Python爬虫逆向系列(更新中):http://t.csdnimg.cn/5gvI3 HTTP 基本原理 在本节中,我们会详细了解 HTTP 的基本原理,了解在浏览器中敲入 URL 到获取网页内容之间发生了什么。了解了这些内容,有助于我们进一…...
iOS17使用safari调试wkwebview
isInspectable配置 之前开发wkwebview的页面的时候一直使用safari调试,毕竟jssdk交互还是要用这个比较方便,虽说用一个脚本插件没问题。不过还是不太方便。 但是这个功能突然到了iOS17之后发现不能用了,还以为又是苹果搞得bug,每…...
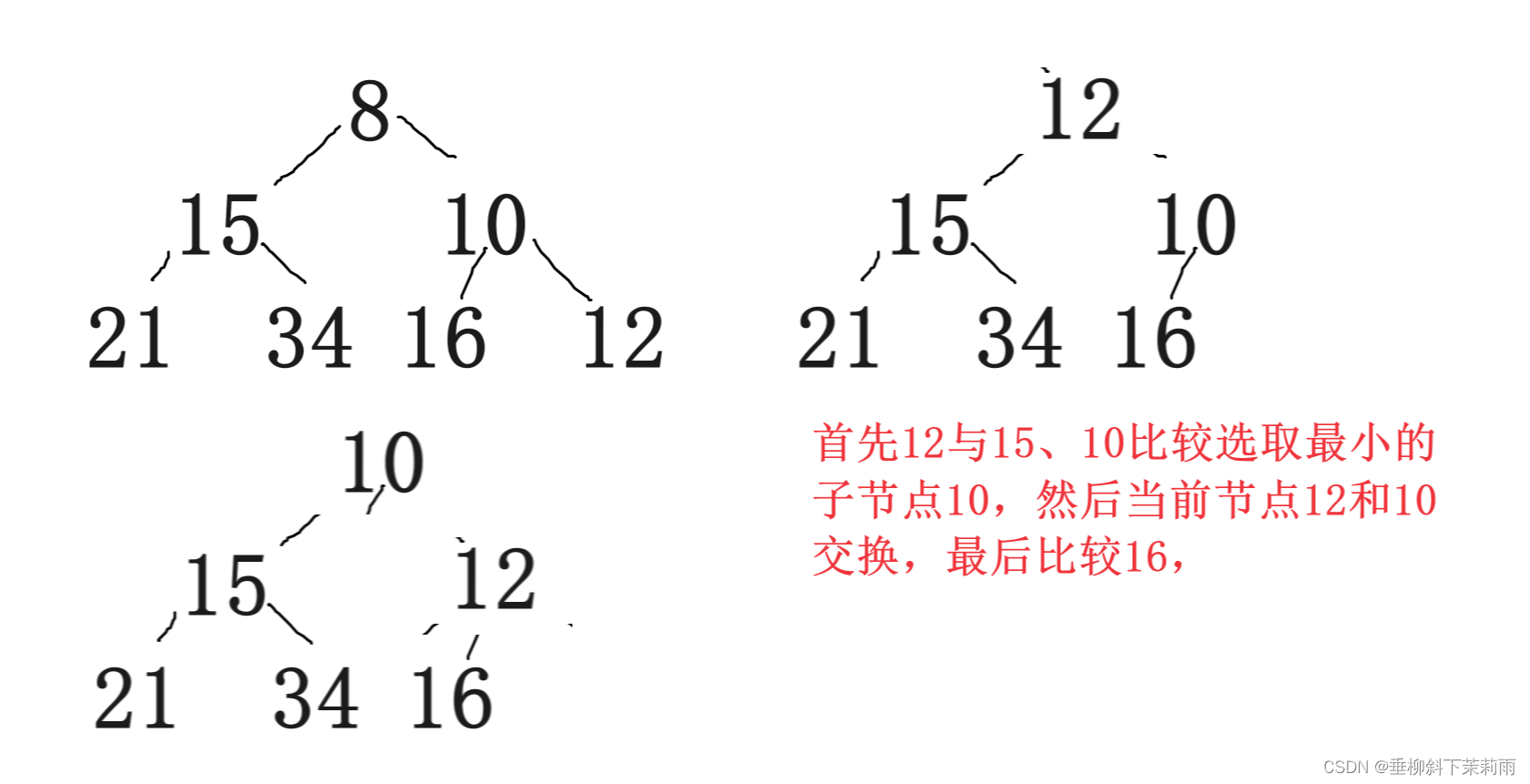
二叉树(1)
1 树概念及结构 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点&a…...

ArcGIS Pro字段编号相关代码
字段属于SHP文件的重要组成部分,在某些时候需要对字段进行编号,这里为大家介绍一下字段编号相关的代码,希望能对你有所帮助。 数据来源 教程所使用的数据是从水经微图中下载的POI数据,除了POI数据,常见的GIS数据都可…...

AJAX-URL查询参数
定义:浏览器提供给服务器的额外信息,让服务器返回浏览器想要的数据 http://xxxx.com/xxx/xxx?参数名1值1&参数名2值2 axios语法 使用axios提供的params选项 注意:axios在运行时把参数名和值,会拼接到url?参数名值 axios(…...
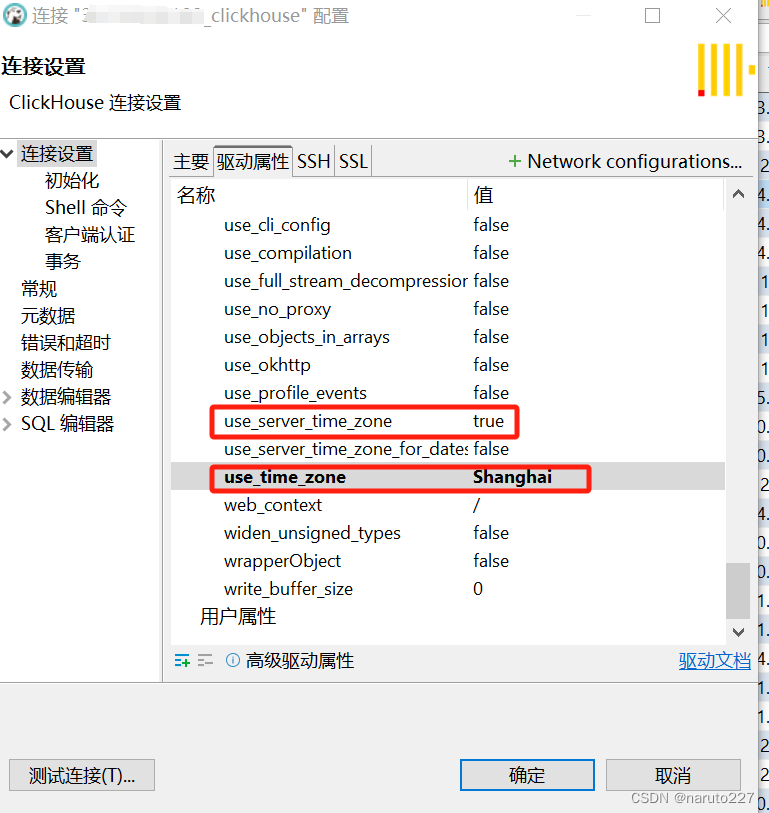
DBeaver连接ClickHouse,时间少了8小时
文章目录 业务场景问题描述解决办法 业务场景 表字段time,类型为Datetime,插入时间格式为“yyyy-MM-dd HH:mm:ss” 问题描述 插入表中的时间比正常给的时间少了8小时。如,给定时间为: 2024-01-30 14:52:08 在表中显示的时间为&…...
)
week03day03(文件操作、正则表达式1)
一、文件操作 1.数据持久化(数据本地化) -- 将数据保存在硬盘 程序中的数据默认是保存在运行内存中的,保存在运行内存中的数据在程序运行结束后会自动释放。如果希望在程序结束后,数据仍可以使用&…...

【数据分享】1929-2023年全球站点的逐年最高气温数据(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标,其中又以气温指标最为常用!说到气温数据,最详细的气温数据是具体到气象监测站点的气温数据! 之前我们分享过1929-2023年全球气象站…...
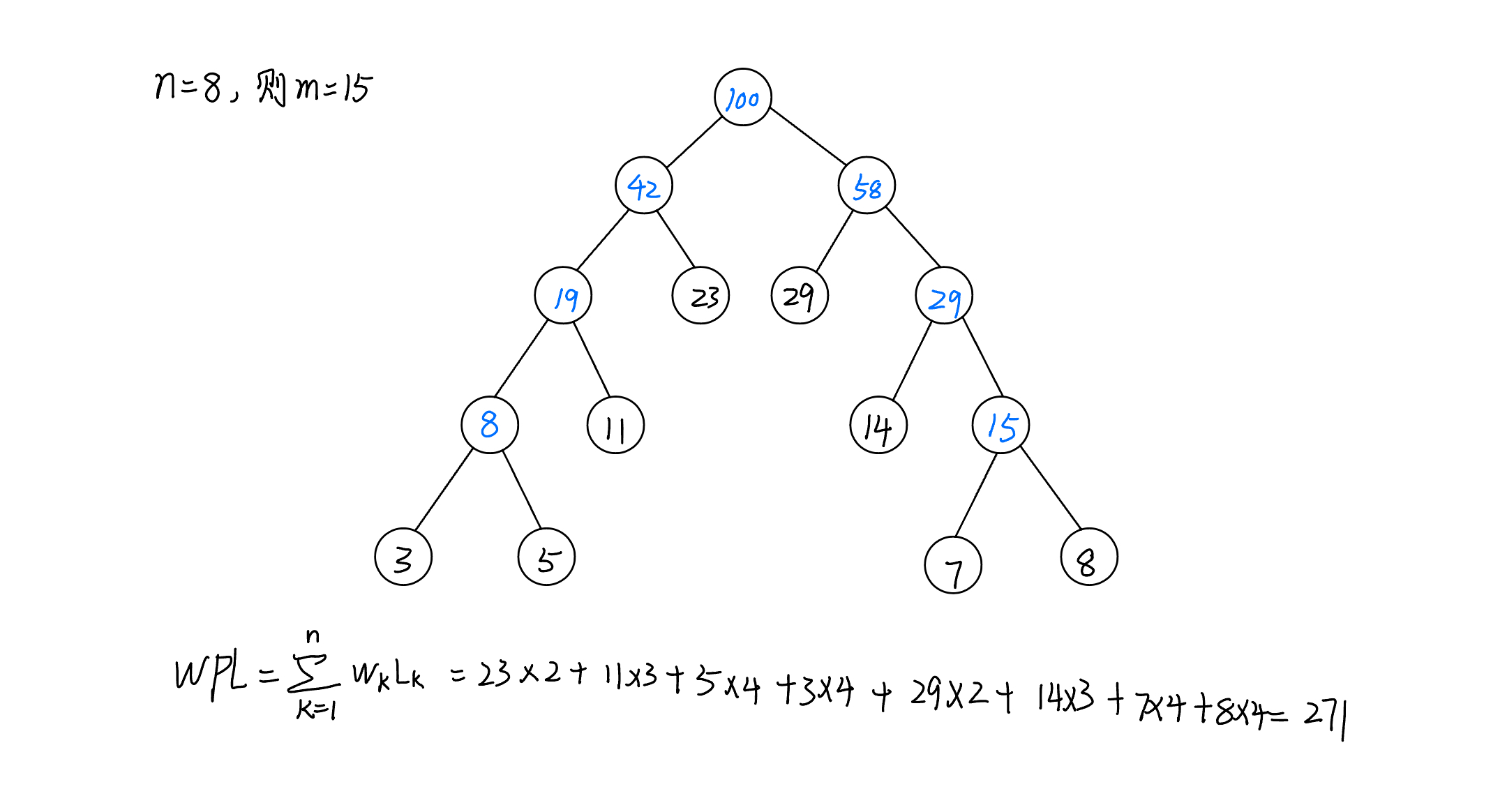
数据结构—基础知识:哈夫曼树
文章目录 数据结构—基础知识:哈夫曼树哈夫曼树的基本概念哈夫曼树的构造算法哈夫曼树的构造过程哈夫曼算法的实现算法:构造哈夫曼树 数据结构—基础知识:哈夫曼树 哈夫曼树的基本概念 哈夫曼(Huffman)树又称最优树&…...
复习提纲24)
计算机网络(第六版)复习提纲24
3 传输控制协议TCP概述 A TCP最主要的特点 1 面向连接的传输层协议 2 每一条TCP连接只能有两个端点,且只能是点对点的 3 提供可靠交付的服务(无差错、不丢失、不重复、不乱序) 4 全双工通信,两端设有发送缓存和接收缓存 5 面向字节…...

[机器学习]TF-IDF算法
一.TF-IDF算法概述 什么是TF-IDF? 词频-逆文档频率(Term Frequency-Inverse Document Frequency,TF-IDF)是一种常用于文本处理的统计方法,可以评估一个单词在一份文档中的重要程度。简单来说就是可以用于文档关键词的提…...

Loadbalancer如何优雅分担服务负荷
欢迎来到我的博客,代码的世界里,每一行都是一个故事 Loadbalancer如何优雅分担服务负荷 前言Loadbalancer基础:数字世界的分配大师1. 分发请求:2. 健康检查:3. 会话保持:4. 可伸缩性:5. 负载均衡…...
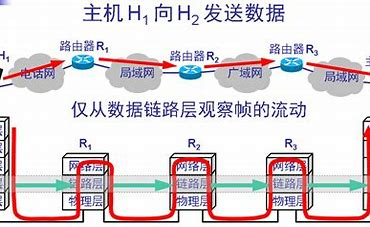
计算机网络——链路层(1)
计算机网络——链路层(1) 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU)前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家, [跳转到网站](https://www.captainbed.…...
OpenCV 0 - VS2019配置OpenCV
1 配置好环境变量 根据自己的opencv的安装目录配置 2 新建一个空项目 3 打开 视图->工具栏->属性管理器 4 添加新项目属性表 右键项目名(我这是opencvdemo)添加新项目属性表,如果有配置好了的属性表选添加现有属性表 5 双击选中Debug|x64的刚添加的属性表 6 (重点)添…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
