【算法】利用递归dfs解决二叉树算法题(C++)
文章目录
- 1. 前言
- 2. 算法题
- 2331.计算布尔二叉树的值
- 129.求根节点到叶节点数字之和
- LCR047.二叉树剪枝
- 98.验证二叉搜索树
- 230.二叉搜索树中第K小的元素
- 257.二叉树的所有路径
1. 前言
有关 递归 的相关解释与解题 请看下文:
以汉诺塔理解递归、并用递归解决算法题
-
对于二叉树,我们曾学过前序遍历,其就是深度优先搜索的一种应用。
- 在二叉树的前序遍历中,我们首先访问根节点,然后递归对左子树进行前序遍历,最后递归地对右子树进行前序遍历。
-
在深度优先搜索算法中,我们从起始节点开始,递归地探索每个可达节点,直到没有未访问的相邻节点为止。因此,前序遍历也可以看作是对图或树进行深度优先搜索的一种方式。它遵循先访问根节点,然后递归地访问左子节点和右子节点的顺序。
2. 算法题
2331.计算布尔二叉树的值
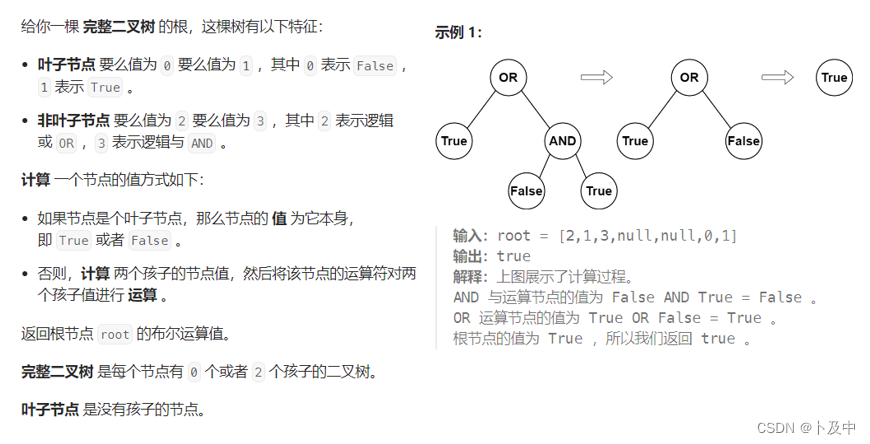
思路
- 题意分析:对于叶子节点有fals,true;对于非叶子节点有|、&;要求算出最终结果,我们只需要进行深搜,遍历一遍二叉树即可。
- 解法:递归dfs + 前序遍历
- 函数体:即前序遍历,分别用bool类型记录左右子树值
- 返回值:当前节点非叶子节点,根据其值判断将左右子树 或还是与
- 函数出口:即递归出口,当遍历到叶子节点后,通过其值向上返回bool类型。
代码
bool evaluateTree(TreeNode* root) {// 递归// 叶子节点为终止条件if(root->left == nullptr && root->right == nullptr)return root->val == 1 ? true : false;bool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2 ? left | right : left & right;
}
129.求根节点到叶节点数字之和
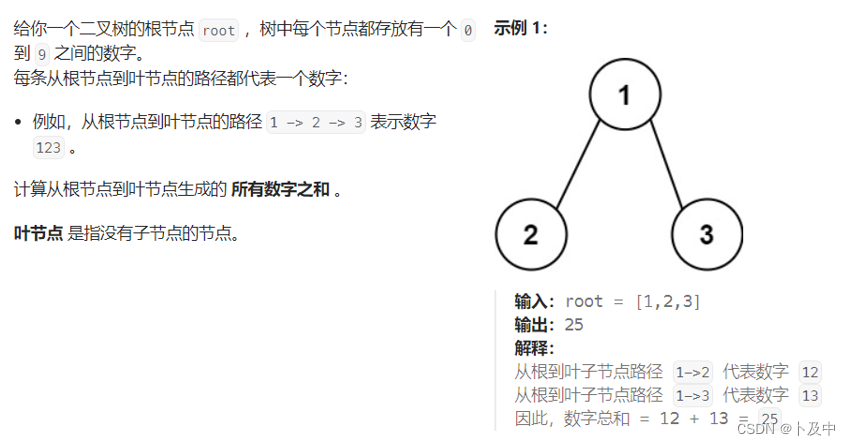
思路
- 题目要求计算二叉树中所有根节点到叶子节点的路径和,如示例所示,对于[1, 2, 3]的最终结果就是两条路径 12 + 13 = 25
- 解法:递归dfs
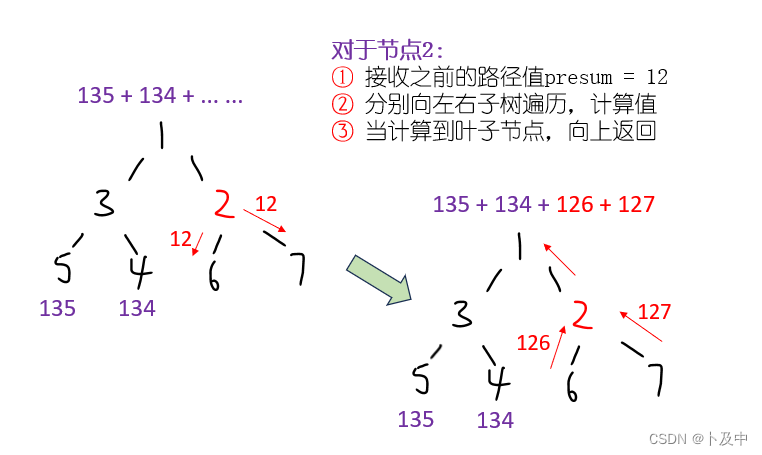
- 思路如上图所示,以此我们可以完成dfs函数:
- 函数头:需要接收一个节点以及到该节点时的路径值,且最终返回的也是总的路径值,即int
dfs(Node* root, int preSum) - 函数体:先统计到当前节点的路径值,再进行左右子树的遍历
- 终止条件:当遍历到叶子节点,向上返回值
- 函数头:需要接收一个节点以及到该节点时的路径值,且最终返回的也是总的路径值,即int
代码
class Solution {
public:// 返回到当前节点计算的所有值int dfs(TreeNode* root, int prevSum) {// 1. 计算prevSum和该节点的数字和int sum = prevSum*10 + root->val;// 2. 终止条件(叶子节点) if(!root->left && !root->right) return sum;// 3.递归左右子树int left = root->left ? dfs(root->left, sum) : 0;int right = root->right ? dfs(root->right, sum) : 0;// 4. 计算出左右子树和并向上返回return left + right;}int sumNumbers(TreeNode* root) {if(!root) return 0;// 递归return dfs(root, 0);}
};
LCR047.二叉树剪枝

思路
- 题意分析:题目要求删除二叉树中所有不包含1的子树,则可以利用递归从后向前进行删除。(即通过后序遍历 删除值为0的叶子节点)
- 解法:递归dfs + 后序遍历
- 函数体:后续遍历,当遇到值为0的叶子节点,将该节点值设为空
- 函数出口:当遍历到空指针时,向上返回。
代码
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {// 后序遍历if(root == nullptr) return nullptr; // 向上返回root->left = pruneTree(root->left);root->right = pruneTree(root->right);if(!root->left && !root->right && root->val == 0) {// delete root; // 释放内存:防止内存泄漏root = nullptr; // 置空}return root;}
};
98.验证二叉搜索树
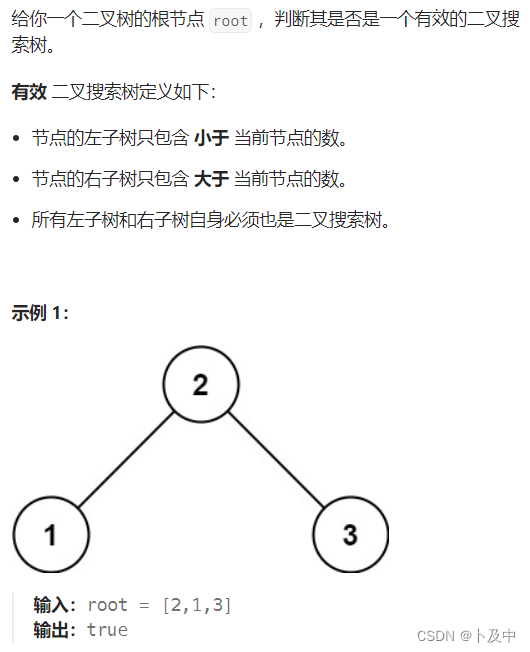
思路
- 题意分析:题目要求验证一棵树是否是二叉搜索树。
- 解法:递归dfs + 中序遍历 + 利用二叉搜索树性质
- 而我们知道,根据二叉搜索树的定义,其中序遍历是有序的,对于BSTree的任意一个节点,其前驱节点一定小于自身
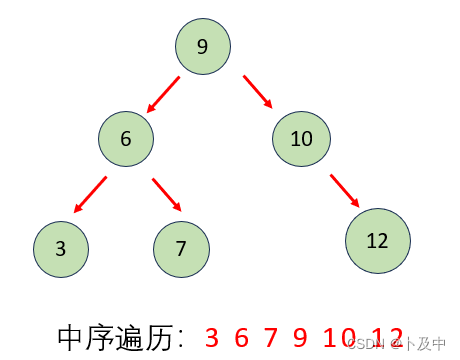
- 据此,我们可以利用中序遍历以及该性质解题:
- 定义 前驱节点以及一个标记符flag用于标记当前节点是否满足条件。
- 函数体:中序遍历,对于当前节点判断:如果其前驱节点存在且大于自身,则不是BSTree,将标记符设为false,递归结束。
- 结束条件:当遍历到空节点或标记符为false时,向上返回
- 而我们知道,根据二叉搜索树的定义,其中序遍历是有序的,对于BSTree的任意一个节点,其前驱节点一定小于自身
代码
class Solution {
public:TreeNode* prev = nullptr; // 定义全局变量,用于找前驱节点bool flag = true;; // 标记树是否是bstree bool isValidBST(TreeNode* root) {// 递归if(root != nullptr && flag){// 中序遍历isValidBST(root->left);// 如果前一个节点的值大于当前节点的值,则不满足二叉排序树的条件if(prev != nullptr && prev->val >= root->val)flag = false;prev = root; // 更新前驱节点isValidBST(root->right);}return flag;}
};
230.二叉搜索树中第K小的元素
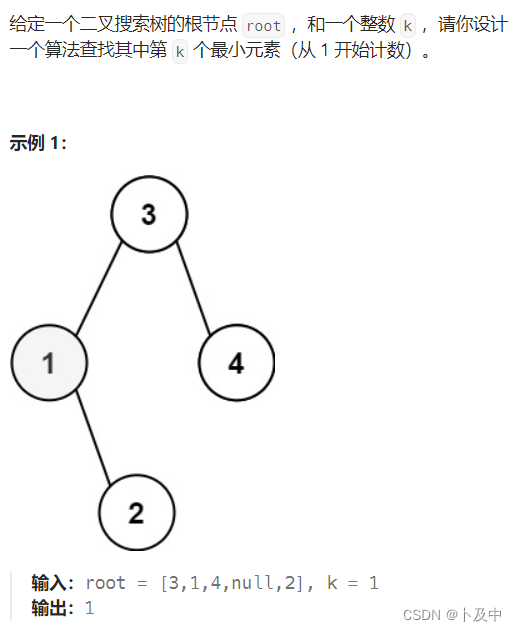
思路
- 题意分析:题目要求找到二叉搜索树的倒数第k个最小元素,依照上题的思路,进行中序遍历即可。
- 解法:递归dfs + 中序遍历 + 利用二叉搜索树性质
- 定义全局变量,省去多次递归创建变量的开销:定义count和ret分别记录k值和结果值
- dfs函数中进行中序遍历,每次递归–count,直到count==0,此时节点的值就是ret
代码
class Solution {
public:// 全局变量解决递归问题int count, ret;void dfs(TreeNode* root) {// 中序遍历if(!root || count == 0) return;dfs(root->left);--count;if(count == 0)ret = root->val;dfs(root->right);}int kthSmallest(TreeNode* root, int k) {count = k;dfs(root);return ret;}
};
257.二叉树的所有路径
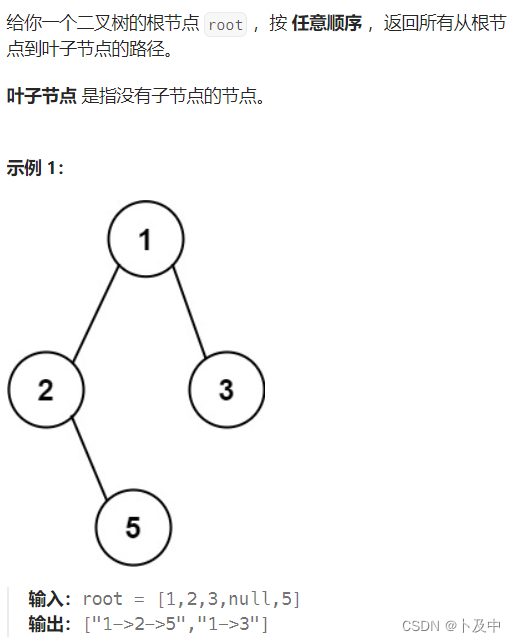
思路
- 题意分析:输出所有从根节点到叶子节点的路径。
- 思路:思路很简单,就是直接使用前序遍历即可,对每个节点都加入到字符串中并对字符串后加箭头。
- 解法:递归dfs + 前序遍历
- 细节问题:
- 叶子节点不需要加箭头,写代码时另外列出
- 其余则是对vector和string的使用
- 细节问题:
代码
class Solution {
public:vector<string> ret; // 最终结果// 如果将path定义为全局变量,则需要手动"恢复现场"// 而作为函数参数,则由函数的性质自动完成了此过程void dfs(TreeNode* root, string path) {// 前序遍历if(root == nullptr) return;// 叶子结点不需要箭头// 将其加入到ret中,并返回if(!root->left && !root->right){path += to_string(root->val);ret.push_back(path);return;}path += to_string(root->val) + "->";dfs(root->left, path);dfs(root->right, path);}vector<string> binaryTreePaths(TreeNode* root) {string path = ""; // 用于记录当前路径dfs(root, path);return ret;}
};
相关文章:

【算法】利用递归dfs解决二叉树算法题(C++)
文章目录 1. 前言2. 算法题2331.计算布尔二叉树的值129.求根节点到叶节点数字之和LCR047.二叉树剪枝98.验证二叉搜索树230.二叉搜索树中第K小的元素257.二叉树的所有路径 1. 前言 有关 递归 的相关解释与解题 请看下文: 以汉诺塔理解递归、并用递归解决算法题 对于…...

计算机网络_1.6.1 常见的三种计算机网络体系结构
1.6.1 常见的三种计算机网络体系结构 1、OSI(七层协议)标准失败的原因2、TCP/IP参考模型3、三种网络体系结构对比 笔记来源: B站 《深入浅出计算机网络》课程 1、OSI(七层协议)标准失败的原因 (1…...
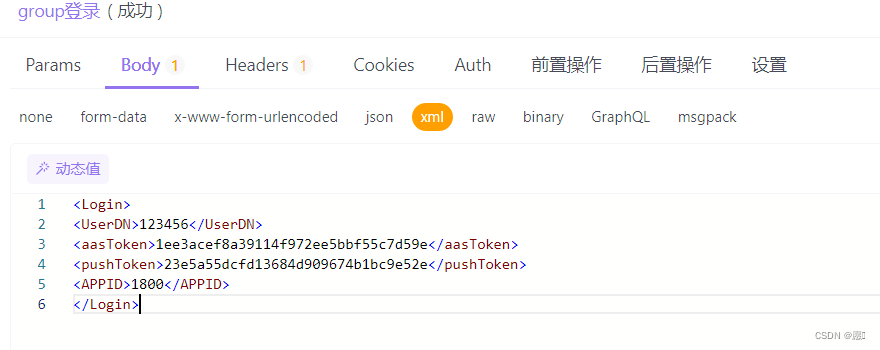
XML传参方式
export function groupLoginAPI(xmlData) {return http.post(/tis/group/1.0/login, xmlData, {headers: {Content-Type: application/xml,X-Requested-With: AAServer/4.0,}}) }import {groupLoginAPI} from "../api/user"; function (e) { //xml格式传参let groupX…...
Pyecharts炫酷散点图构建指南【第50篇—python:炫酷散点图】
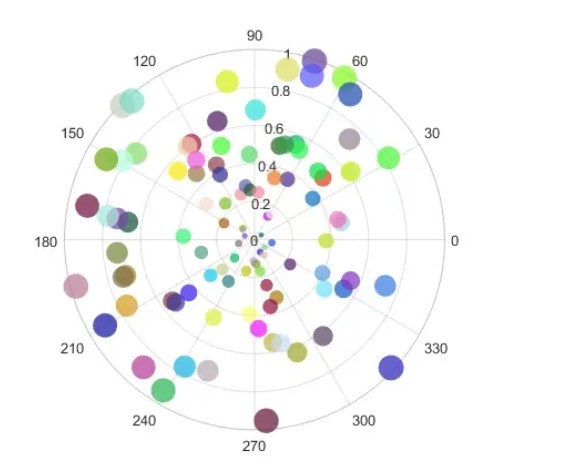
文章目录 Pyecharts炫酷散点图构建指南引言安装Pyecharts基础散点图自定义散点图样式渐变散点图动态散点图高级标注散点图多系列散点图3D散点图时间轴散点图笛卡尔坐标系下的极坐标系散点图 总结: Pyecharts炫酷散点图构建指南 引言 在数据可视化领域,…...
关于爬取所有哔哩哔哩、任意图片、所有音乐、的python脚本语言-Edge浏览器插件 全是干货!
这些都是现成的并且实时更新的!从次解放双手! 首先有自己的edge浏览器基本上都有并且找到插件选项 1.哔哩哔哩视频下载助手(爬取哔哩哔哩视频) bilibili哔哩哔哩视频下载助手 - Microsoft Edge Addons 下面是效果: 2.图…...
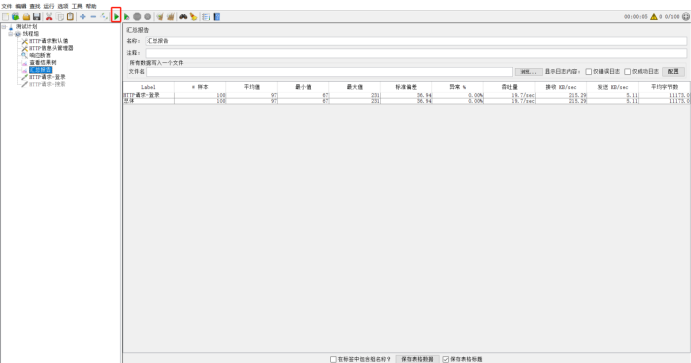
压力测试工具-Jmeter使用总结
目录 一.前言 二.线程组 三.线程组的组件 四.线程组-HTTP请求 1、JSON提取器 2、XPATH提取器 3、正则表达式提取器 五.线程组-断言 1、响应断言 2、JSON断言 六.创建测试 1.创建线程组 2.配置元件 3.构造HTTP请求 4.添加HTTP请求头 5.添加断言 6.添加查看结果树…...

[cmake]CMake Error: Could not create named generator Visual Studio 16 2019解决方法
配置flycv时,cmake以下代码会报错第二行的错误,网上解决方法为第三行代码 cmake .. -G "Visual Studio 16 2019 Win64" CMake Error: Could not create named generator Visual Studio 16 2019 cmake .. -G "Visual Studio 16 2019"…...

2024美赛数学建模D题思路分析 - 大湖区水资源问题
1 赛题 问题D:大湖区水资源问题 背景 美国和加拿大的五大湖是世界上最大的淡水湖群。这五个湖泊和连接的水道构成了一个巨大的流域,其中包含了这两个国家的许多大城市地区,气候和局部天气条件不同。 这些湖泊的水被用于许多用途࿰…...

2024 高级前端面试题之 HTTP模块 「精选篇」
该内容主要整理关于 HTTP模块 的相关面试题,其他内容面试题请移步至 「最新最全的前端面试题集锦」 查看。 HTTP模块精选篇 1. HTTP 报文的组成部分2. 常见状态码3. 从输入URL到呈现页面过程3.1 简洁3.2 详细 4. TCP、UDP相关5. HTTP2相关6. https相关7. WebSocket的…...

【Linux C | 网络编程】netstat 命令图文详解 | 查看网络连接、查看路由表、查看统计数据
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

Python爬虫存储库安装
如果你还没有安装好MySQL、MongoDB、Redis 数据库,请参考这篇文章进行安装: Windows、Linux、Mac数据库的安装(mysql、MongoDB、Redis)-CSDN博客 存储库的安装 上节中,我们介绍了几个数据库的安装方式,但…...
)
用函数求最小公倍数和最大公约数(c++题解)
题目描述 输入两个正整数m和n,求其最大公约数和最小公倍数。 提示,求最大公约数用一个函数实现。本题求最大公约数必须用高效算法,如辗转相除法,朴素算法要超时。 输入格式 第1行:两个非整数,值在0&…...

鲜花销售|鲜花销售小程序|基于微信小程序的鲜花销售系统设计与实现(源码+数据库+文档)
鲜花销售小程序目录 目录 基于微信小程序的鲜花销售系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、前台功能模块 2、后台功能模块 (1) 后台登录 (2) 管理员功能模块 用户管理 商家管理 鲜花信息管理 鲜花分类管理 管理员管理 系统管理 (3) 商家功…...

三.Linux权限管控 1-5.Linux的root用户用户和用户组查看权限控制信息chmod命令chown命令
目录 三.Linux权限管控 1.Linux的root用户 root用户(超级管理员) su和exit命令 sudo命令 为普通用户配置sudo认证 三.Linux权限管控 2.用户和用户组 用户,用户组 用户组管理 用户管理 getent---查看系统中的用户 三.Linux权限管控…...
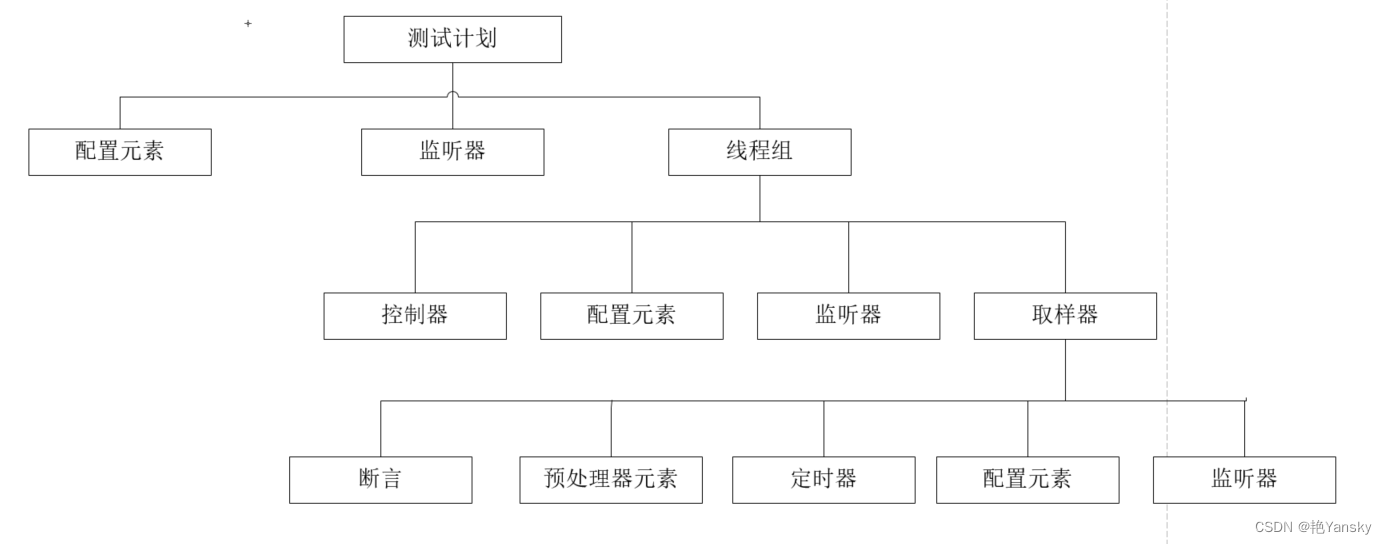
Jmeter学习系列之四:测试计划元素介绍
测试计划元素 JMeter包含各种相互关联但为不同目的而设计的元素。在开始使用JMeter之前,最好先了解一下JMeter的一些主要元素。 注意:测试计划包含至少一个线程组。 以下是JMeter的一些主要组件: 测试计划(Plan)线程组(Thread Group)控制器…...
LeetCode.1686. 石子游戏 VI
题目 题目链接 分析 本题采取贪心的策略 我们先假设只有两个石头a,b, 对于 Alice 价值分别为 a1,a2, 对于 Bob 价值而言价值分别是 b1,b2 第一种方案是 Alice取第一个,Bob 取第二个,Alice与Bob的价值差是 c1 a1 - b1…...

【硬件产品经理】锂电池充电时间怎么计算?
目录 前言 电池容量 充电器功率 电能转换效率 充电时间计算 作者简介<...

Oracle篇—普通表迁移到分区表(第五篇,总共五篇)
☘️博主介绍☘️: ✨又是一天没白过,我是奈斯,DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux,也在积极的扩展IT方向的其他知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章,并且也会默默的点赞收藏加关注❣…...

作为开发人的我们,怎么可以不了解这些?
必备技能: 文章结尾处,有资源获取方式 Spring Spring是一个轻量级的Java框架,它可以用于开发各种Java应用程序。Spring提供了丰富的功能,包括IoC容器、AOP、事务管理、Web开发、安全管理等等。Spring的IoC容器可以…...

基于 Echarts 的 Python 图表库:Pyecahrts交互式的日历图和3D柱状图
文章目录 概述一、日历图和柱状图介绍1. 日历图基本概述2. 日历图使用场景3. 柱状图基本概述4. 柱状图使用场景 二、代码实例1. Pyecharts绘制日历图2. Pyecharts绘制2D柱状图3. Pyecharts绘制3D柱状图 总结 概述 本文将引领读者深入了解数据可视化领域中的两个强大工具&#…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
