Linux-正则表达式
1.正则表达式的定义:
正则表达式通常用于判断语句中,使用字符串描述、匹配一系列符合某个规则的字符串。
正则表达式是由普通字符与元字符组成。
- 普通字符包括小写字母、数字、标点符号及一些其他符号。
- 元字符是指在正则表达式中具有特殊意义的专用字符,可以用来规定其前导字符(即位于元字符前面的字符)在目标对象中的出现模式。
(正则表达式模式都区分大小写)
2.正则表达式的分类:
正则表达式根据从POSIX BRE或者POSIX ERE标准可以分为:
- 基本正则表达式
- 扩展正则表达式
可以使用:
man 7 regex
(可以使用 man手册帮助)
3.文本三剑客(grep sed awk)支持的正则表达式:
shell是不支持正则表达式的(shell支持的是通配符)。shell中的正则表达式只有个别命令支持的,一般常用的是文本三剑客。
| 支持正则的shell命令 | 正则类型 |
| grep | 默认使用基本正则表达式(BRE)(要使用扩展正则需要加转义字符) |
| sed | 默认使用基本正则表达式(BRE) |
| awk | 使用扩展正则表达式(ERE) |
| egrep 或 grep -E | 使用扩展的正则表达式(ERE) |
4.基本正则表达式:
支持的工具:grep、egrep、sed、 awk。(注意grep要配合-E或者-P使用)
| 元字符 | 含义及用法 |
| \ | 表示转义字符,去掉特殊符号的特殊含义 |
| . | 匹配任意单个字符 |
| ^ | 匹配字符串开头的位置 |
| $ | 匹配字符串末尾的位置 |
| * | 匹配前面的字符出现0~+∞ |
| [list] | 匹配list列表中的一个字符(列表中只要有一个符合即可) |
| [^list] | 匹配任意非list列表中的一个字符 |
| {n} | 匹配前面的子表达式n次 |
| {n,} | 匹配前面的子表达式最少n次 |
| {,n} | 匹配前面的子表达式最多n次 |
| {n,m} | 匹配前面的子表达式n到m次 |
| [ ] | 代表单个字符 |
| \? | 1次或0次 |
| ^$ | 空行 |
| .* | 1~+∞ |
4.1转义字符的运用:
将特殊含义的字符转换为普通字符的含义:
| 被转义的特殊字符 | 转义前的含义作用 |
| \ = | 具有赋值的作用,或则进行字符判断 |
| \ ! | 取反 |
| \ & | 单个&符可以将命令挂在后台上,两个是逻辑符号且的作用 |
| \ $ | 取值变量的作用 |
将普通字符转换为特殊作用的字符:
| 被赋予新含义的普通字符 | 现在拥有的作用 |
| \n | 换行 |
| \t | 转化为制表符 |
| \w(小写) | 匹配包括下划线的任何单词字符 |
| \W(大写) | 匹配任何非单词字符。等通于"[^A-Za-z0-9_]" |
| \r | 转换后是回车符 |
| \d | 匹配一个数字字符 |
| \D | 匹配一个非数字字符。等价于[^0-9] |
| \s(小写) | 空白符 |
| \S(大写) | 非空白符 |
4.2.中括号表达式:
普通中括号包围的字符组,表示某个单个字符匹配中括号内的任意字符即匹配成功
- x[abc]z : 可以匹配包含“xaz”、“xbz”、“xcz”的字符串
- 取反表示法: 中括号内开头使用 ^ ,表示只要不是中括号内的字符就匹配
x[ ^abc]z : 可以匹配包含 “xdz”、“xez” 等字符串,但不能匹配包含“xaz”、“xbz”、“xcz”的字符串
特殊元字符在中括号中匹配:
- 想要在中括号中匹配: ^ ,需要将其放在 中括号非开头的位置 ,如:[a^]
- 想要在中括号中匹配: - ,需要将其放在 开头位置或结尾位置 ,如:[abc-]、[-abc]
- 想要在中括号中匹配: ] ,需要将其放在 开头位置 ,如:[]abc]
位置匹配:
^ : 匹配行首
$ : 匹配行尾
\b 匹配单词边界处的位置(开头和结尾) \bword\b 等价于 \<word\>
\< 匹配单词开头处的位置
\> 匹配单词结尾处的位置
\B 匹配非单词边界处的位置
字符类:
| [:alnum:] | 字母和数字 |
| [:alpha:] | 代表任何英文大小写字母 A-Z a-z |
| [:lower:] | 小写字母 |
| [:upper:] | 大写字母 |
| [:blank:] | 空白字符 |
| [:space:] | 包括空格、制表符 (水平和垂直)、换行符、回车符等各种类型的空白,比[:blank:]包含的范围广 |
| [:cntrl:] | 不可打印的控制字符(退格、删除、警铃...) |
| [:digit:] | 十进制数字 |
| [:xdigit:] | 十六进制数字 |
| [:graph:] | 可打印的非空白字符 |
| [:print:] | 可打印字符 |
| [:punct:] | 标点符号 |
量词:
\{m\} : 表示匹配前一个字符或前一个子表达式m次
\{m,n\} : (m<n)表示匹配前一个字符或前一个字表达式最少m次,最多n次
\{m,\} : 表示匹配前一个字符或前一个子表达式至少m次
\{,n\} : 表示匹配前一个字符或前一个字表达式最多n次(匹配0次也算是成功)
* 表示前一个字符或前一个子表达式匹配0次或多次,等价于:{0,}
.* 匹配任意长度的任意字符
5.扩展正则表达式的元字符:
egrep 默认使用的 是扩张正则
支持的工具:egrep、awk,注意:使用grep要配合-E或者-P使用,sed要配合-r使用。
| 元字符 | 含义及用法 |
| + | 匹配前面子表达式1次以上,例: go+d,将匹配至少一个o,如god、good、goood等 |
| ? | 匹配前面子表达式0次或者1次,例: go?d,将匹配gd或god |
| () | 将括号中的字符串作为一个整体,例1: g(oo)+d,将匹配oo整体1次以上,如good、gooood等 |
| | | 以或的方式匹配字符串,例:g(oo|la)d,将匹配good或者 glad |
| * | 匹配前面字符任意次 |
| {n} | 匹配n次 |
| {m,n} | 至少m,至多n次 |
扩展常用的量词:
- + 表示匹配前一个字符或前一个子表达式1或多次,即至少一次 等价于 {1, }
- ? 表示匹配前一个字符或前一个子表达式0或1次,等价于 {0,1} 等价于 {,1}
分组捕获和反向引用:
使用小括号()包围一部分正则表达式,这部分正则表达式即成为一个分组整体,也称为一个子表达式。
分组后可以使用 \N 来反向引用对应的分组匹配结果,N是1-9的正整数,\1表示第一个分组表达式的匹配结果,\2表达第二个分组表达式的匹配结果。
注意:反向引用引用的是分组匹配后的结果,不是分组表达式
例如:正则表达式:(abc|def) and \1xyz 可以匹配字符串“abc and abcxyz ” 或“def and defxyz”,但是不能匹配“abc and defxyz” 或 “def and abcxyz”
相关文章:
Linux-正则表达式
1.正则表达式的定义: 正则表达式通常用于判断语句中,使用字符串描述、匹配一系列符合某个规则的字符串。 正则表达式是由普通字符与元字符组成。 普通字符包括小写字母、数字、标点符号及一些其他符号。元字符是指在正则表达式中具有特殊意义的专用字符&…...

Java基础学习:System类和Static方法的实际使用
一、System类 1.在程序开发中,我们需要对这个运行的结果进行检验跟我们预判的结果是否一致,就会用到打印结果在控制台中显示出来使用到了System类。System类定义了一些和系统相关的属性和方法,它的属性和方法都是属于静态的,想使用…...
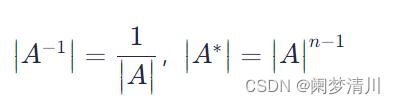
线性代数------矩阵的运算和逆矩阵
矩阵VS行列式 矩阵是一个数表,而行列式是一个具体的数; 矩阵是使用大写字母表示,行列式是使用类似绝对值的两个竖杠; 矩阵的行数可以不等于列数,但是行列式的行数等于列数; 1.矩阵的数乘就是矩阵的每个…...

Flutter 开发3:创建第一个Flutter应用
Step 1: 安装Flutter 1.1 下载Flutter SDK 首先,你需要访问Flutter官方网站下载最新的Flutter SDK。选择适合你操作系统的安装包。 $ cd ~/development $ unzip ~/Downloads/flutter_macos_2.2.3-stable.zip1.2 更新环境变量 接下来,你需要将Flutter…...

Linux中断下半部分:软中断,tasklet和工作队列
为什么要有下半部分 中断会打断其他程序,为了打断其他程序时间短,就需要中断处理程序快。执行中断处理程序后,相同中断不会触发,甚至所有中断都不能触发(设置IRQF_DISABLED,其他硬件与操作系统无法通信)中…...
Flink CEP实现10秒内连续登录失败用户分析
1、什么是CEP? Flink CEP即 Flink Complex Event Processing,是基于DataStream流式数据提供的一套复杂事件处理编程模型。你可以把他理解为基于无界流的一套正则匹配模型,即对于无界流中的各种数据(称为事件),提供一种组合匹配的…...
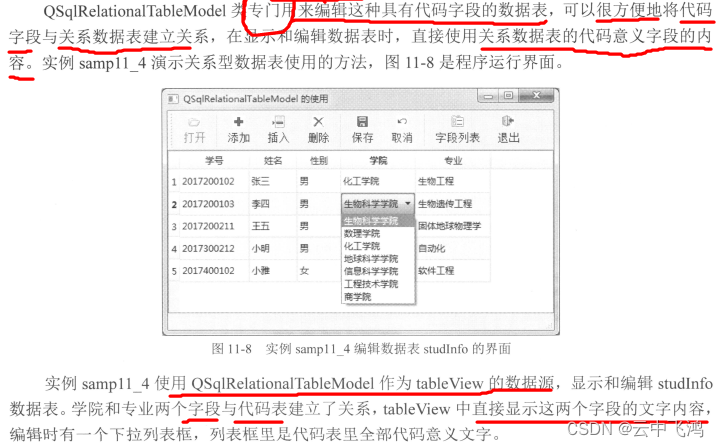
QSqlRelationalTableModel 关系表格模型
一、 1.1 QSqlRelationalTableModel继承自QSqlTableModel,并且对其进行了扩展,提供了对外键的支持。一个外键就是一个表中的一个字段 和 其他表中的主键字段之间的一对一的映射。例如,“studInfo”表中的departID字段对应的是“departments…...

JS和CSS实现的原生轮播图
JSCSS实现滑动轮播图 使用JS加CSS来实现的幻灯片,主要使用的是CSS的transform属性中的translate来实现,适合与用户交互的轮播图,展现轮播图的数量,用户可自由进行选择。 <!DOCTYPE html> <html lang"en">&…...
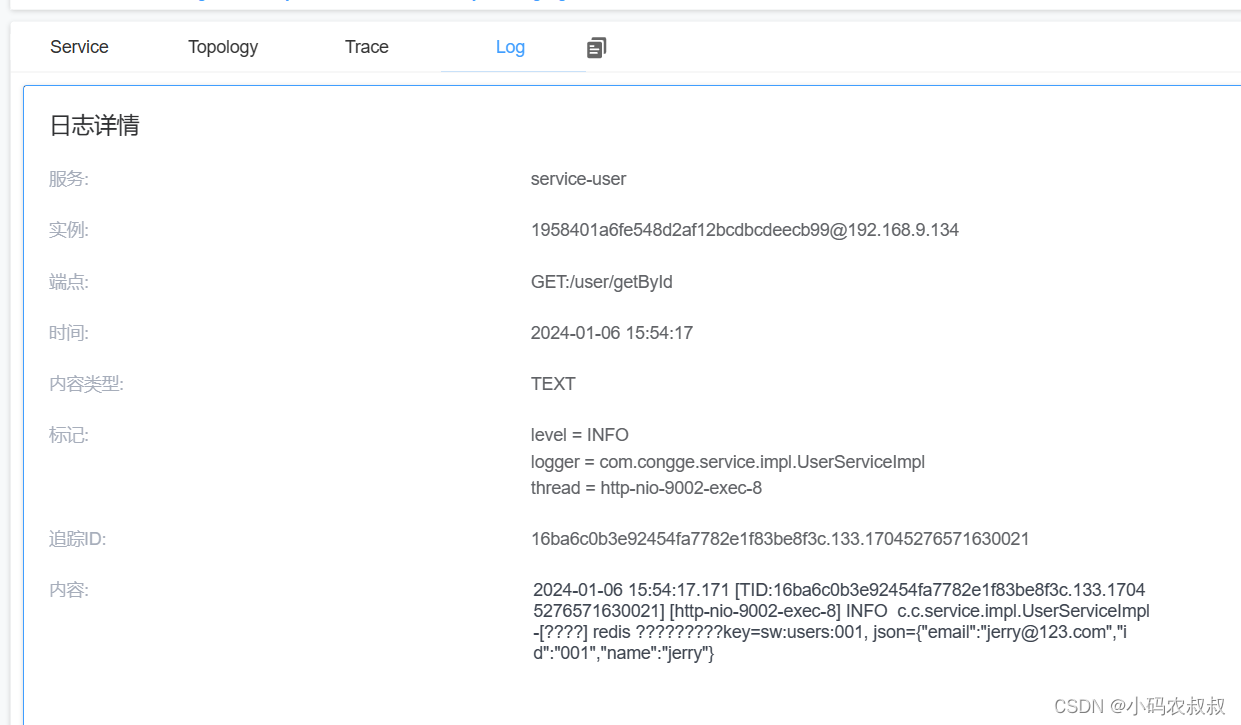
【微服务】skywalking自定义链路追踪与日志采集
目录 一、前言 二、自定义链路追踪简介 2.1 自定义链路追踪应用场景 2.2 链路追踪几个关键概念 三、skywalking 自定义链路追踪实现 3.1 环境准备 3.2 集成过程 3.2.1 导入核心依赖 3.2.2 几个常用注解 3.2.3 方法集成 3.2.4 上报追踪信息 四、skywalking 自定义日志…...

MYSQL基础问题
一.DBMS 是什么 DBMS(Database Management System),数据库管理系统,是一种操纵和管理 数据库的大型软件,用于建立、使用和维护数据库。对数据库进行统一的管理和 控制,以保证数据库的安全性和完整性。 二…...
)
SpringBoot使用Guava实现日志脱敏(含源码)
点击下载《SpringBoot使用Guava实现日志脱敏(含源码)》 1. 摘要 本文将介绍如何使用Google Guava库进行日志脱敏,保护敏感数据的安全。我们将详细解释脱敏的必要性,然后介绍如何使用Guava中的Strings、Maps和CharMatcher类来进行…...
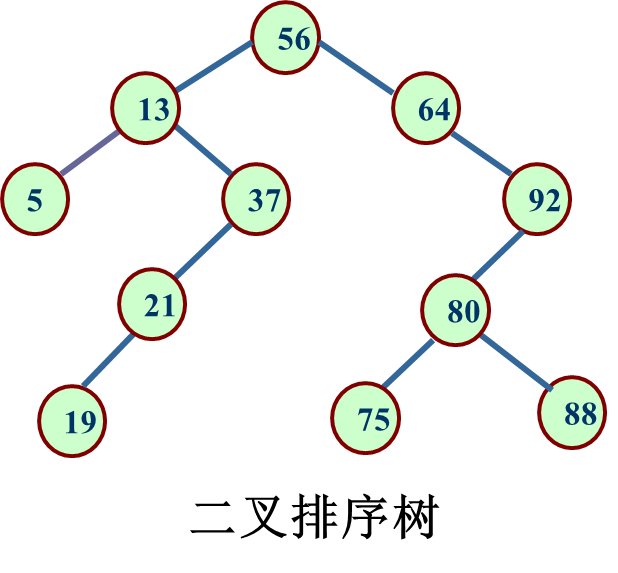
数据结构—动态查找
动态查找介绍 1. 动态查找的引入:当查找表以线性表的形式组织时,若对查找表进行插入、删除或排序操作,就必须移动大量的记录,当记录数很多时,这种移动的代价很大。 2. 动态查找表的设计思想:表结构本身是…...

Tarjan算法学习笔记
目录 无向图的割点与桥 时间戳: 搜索树: 追溯值: 割边判定法则: 割点判定法则: 无向图的双连通分量 定理: 边双连通分量(e-DCC)的求法: e-DCC的缩点: 有向图的连通性 追…...

vue 项目涉及的焦点聚焦、格式化日期、判断是否为对象或数组、判断是否为空、深拷贝、节流、防抖
焦点聚焦 import Vue from vue // 插件对象(必须有 install 方法, 才可以注入到 Vue.use 中) export default {install () {Vue.directive(fofo, {inserted (el) {el el.querySelector(input)el.focus()}})} }格式化日期格式 export const formatDate (time) > {// 将xx…...
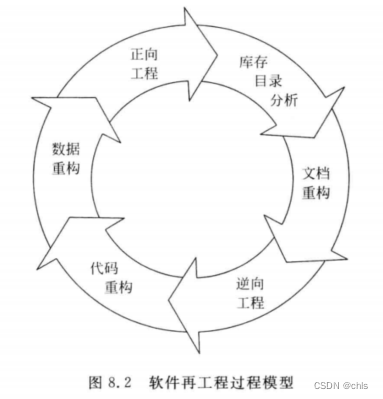
软件工程知识梳理6-运行和维护
软件维护需要的工作量很大,大型软件的维护成本高达开发成本的4倍左右。所以,软件工程的主要目的就是要提高软件的可维护性,减少软件维护所需要的工作量,降低软件系统的总成本。 定义:软件已经交付使用之后,…...

docker- php7.4
安装 gd拓展 anzhuanga在Dockerfile里面安装php7.4的GD库 - 知乎 apt update apt install -y libwebp-dev libjpeg-dev libpng-dev libfreetype6-devdocker-php-source extractdocker-php-ext-configure gd \ --with-jpeg/usr/include \ --with-freetype/usr/include/docker-…...

开发一个Android App,在项目中完成添加联系人的功能,通过ContentResolver向系统中添加联系人信息。
实现步骤: (1)添加动态联系人的权限。 (2)创建Activity和布局文件,添加输入框和按钮等控件。 (3)完成添加联系人的功能。 代码文件如下: activity_main.xml文件 <!…...

Flume搭建
压缩包版本:apache-flume-1.9.0-bin.tar 百度盘链接:https://pan.baidu.com/s/1ZhSiePUye9ax7TW5XbfWdw 提取码:ieks 1.解压 tar -zxvf /opt/software/apache-flume-1.9.0-bin.tar.gz -C /opt/module/ 2. 修改文件名 [rootbigdata1 opt]…...

Web APIs 1 DOM操作
Web APIs 1 引入:const优先Web API 基本认知01 作用和分类02 什么是DOM03 DOM树04 DOM对象 获取DOM对象01 根据CSS选择器获取02 其他获取DOM元素方法 操作元素内容01 innerText 属性02 innerHTML 属性 操作元素属性操作元素的常用属性操作元素的样式属性操作表单元素…...
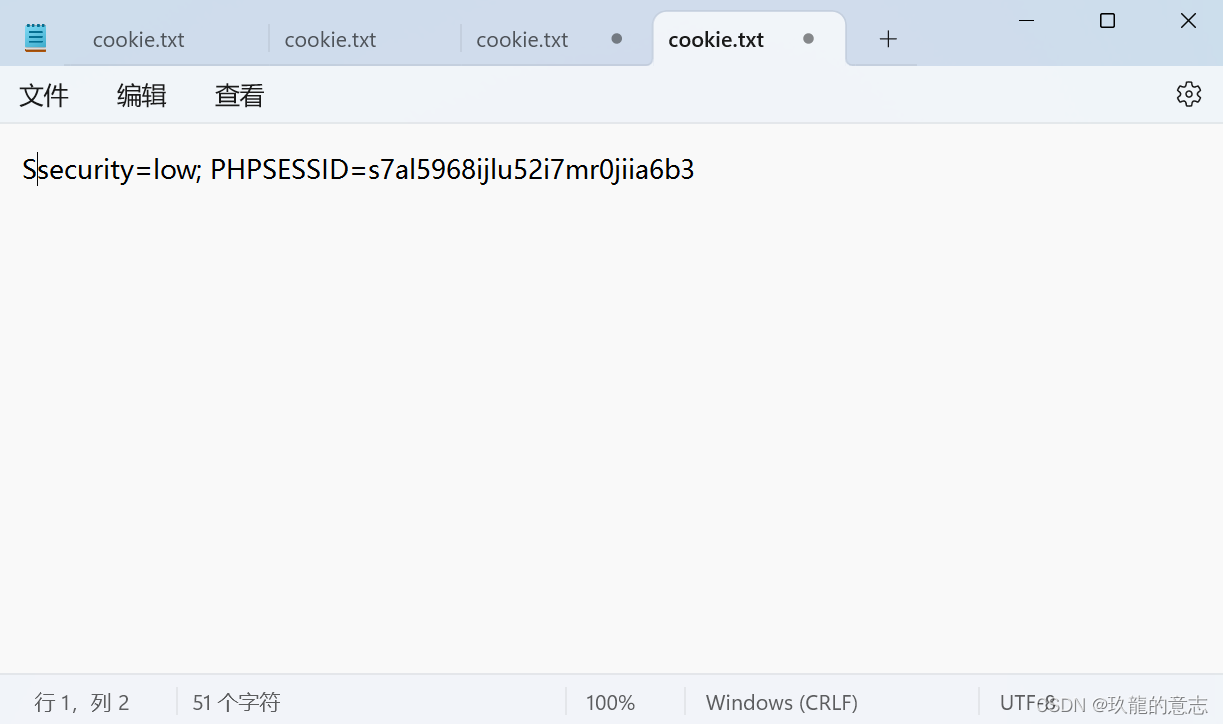
dvwa,xss反射型lowmedium
xss,反射型,low&&medium low发现xss本地搭建实操 medium作为初学者的我第一次接触比较浅的绕过思路high low 发现xss 本关无过滤 <script>alert(/xss/)</script> //或 <script>confirm(/xss/)</script> //或 <scr…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
