【图论】网络流
网络流目前只整理模板,学习的话这篇博客可能不太适合
代码参考下方博客,加了一些自己的注释
- 算法学习笔记(28): 网络流
- 究级的最大流算法:ISAP与HLPP
FF 和 EK 仅用作理解代码,赛时请使用 Dinic 或 ISAP
下文建图方式都基于链式前向星,请注意,cnt 必须从 1 开始!!!!
void add(int u, int v, int val)
{cnt ++ ;node[cnt].to = v;node[cnt].w = val;node[cnt].next = head[u];head[u] = cnt;
}
文章目录
- Ford-Fulkerson (FF算法)
- Edmond-Karp (EK算法)
- Dinic算法
- Improved Shortest Augumenting Path (ISAP算法)
Ford-Fulkerson (FF算法)
基于dfs的最大流算法
时间复杂度 O ( e f ) O(ef) O(ef),e是边数,f是最大流
int n, m, start, end; // start是源点,end是汇点
bool st[MAXN]; // 标记某个点有没有被访问过struct edges
{int to, w, next;
};int dfs(int u, int flow) // u表示当前结点 flow表示目前流量
{if (p == t) return flow; // 到达终点,返回这条增广路的流量st[p] = true; // 标记已经访问过该点for (int eg = head[p]; eg != -1; eg = edges[eg].next) // 遍历所有邻接点{int to = edges[eg].to, w = edges[eg].w, c;if (w <= 0) continue; // 这条边不能再流过流量if (st[to]) continue; // 已经经过该点c = dfs(to, min(w, flow)); // 递归判断接下来能否到达终点 传递下去的流量是边的容量w与当前流量flow中的较小值if (c != -1) // 可以到达终点{edges[eg].w -= c; // 正向边容量w减去流量cedges[eg ^ 1].w += c; // 反向边容量w加上流量c// 建图时要把cnt置为1,且要保证反向边紧接着正向边建立return c; // 返回值是流量}}return -1; // 无法到达终点
}int FF()
{int ans = 0, c; // ans代表总流量while ((c = dfs(start, INF)) != -1) // 只要还可以到达终点就一直dfs下去{memset(st, 0, sizeof(st)); // 初始化每个点的访问状态ans += c; // 加上本次dfs的流量}return ans;
}
Edmond-Karp (EK算法)
基于bfs的最大流算法
时间复杂度 O ( v e 2 ) O(ve^2) O(ve2),v是点数,e是边数
// last表示该条增广路中通向该点的边的编号 flow表示每个点可以流过的最大流量(也就是从上一个点传过来的流量)
int n, m, start, end, last[MAXN], flow[MAXN]; struct edges
{int to, w, next;
};int bfs()
{memset(last, -1, sizeof(last)); // 初始化每个点的增广路径queue<int> q;q.push(start);flow[start] = INF; // 源点可以流过的流量初始化为无穷大while (!q.empty()){int u = q.front();q.pop();if (u == t) break; // 到达汇点,结束搜索for (int eg = head[u]; eg != -1; eg = edges[eg].next) // 遍历所有邻接点{int to = edges[eg].to, w = edges[eg].w;if (w > 0 && last[to] == -1) // 如果残余容量大于0且未访问过(所以last保持在-1){last[to] = eg; // 记录点to在本条增广路的上一条边的编号是egflow[to] = min(flow[p], w); // 取边的容量和上一个点可以流过的流量的最小值q.push(to); // 新点入队}}}return last[end] != -1; // 如果汇点没有访问到,说明没有可以通向汇点的路了
}int EK()
{int maxflow = 0; // maxflow代表总流量while (bfs()) // 只要还可以到达终点就一直bfs下去{maxflow += flow[end]; // 更新总流量 也就是加上能流到汇点的流量for (int i = end; i != start; i = edges[last[i] ^ 1].to) // 从汇点原路返回更新残余容量{edges[last[i]].w -= flow[end]; // 正向边容量w减去该条增广路流量flow[end]edges[last[i] ^ 1].w += flow[end]; // 反向边容量w加上该条增广路流量flow[end]}}return maxflow;
}
Dinic算法
基于FF和EK的最大流算法
时间复杂度 O ( n 2 e ) O(n^2e) O(n2e),n是点数,e是边数
先使用bfs分层,再使用dfs搜索,每次只往层数高的地方走,可以避免走重复的路径
优化:
- 多路增广:在某点找到一条增广路,如果流量没用完,就接着往下bfs
- 当前弧优化:在Dinic中每条边只会增广一次,所以下次增广就不需要考虑已经增广过的边,通过修改起始结点可以实现这个优化
注意:Dinic用在二分图中复杂度是 O ( v e ) O(v\sqrt{e}) O(ve),v是点数,e是边数 ,优于匈牙利算法。
int n, m, start, end, dep[MAXN], cur[MAXN]; // dep是每个点的层数 cur用于当前弧优化标记增广起点struct edges
{int to, w, next;
};bool bfs() // BFS分层
{memset(dep, -1, sizeof(dep)); // 初始化点的层数dep[start] = 0; // 初始化源点的层数为0memcpy(cur, head, sizeof(head)); // 当前弧优化初始化queue<int> q;q.push(start); // 源点入队while (!q.empty()){int u = q.front();q.pop();for (int eg = head[u]; eg; eg = edges[eg].next) // 遍历所有邻接点{int to = edges[eg].to, w = edges[eg].w;if (w > 0 && dep[to] == -1) // dep为-1说明没访问过{dep[to] = dep[u] + 1; // 更新to点层数q.push(to);}}}return dep[end] != -1; // 如果汇点未访问过说明已经无法达到汇点,此时返回false
}int dfs(int u, int flow) // u表示当前结点 flow表示目前流量
{if (u == end) return flow; // 找到汇点 返回目前的流量int rmn = flow; // rmn表示剩余的流量for (int eg = cur[u]; eg != -1; eg = edges[eg].next) // 遍历所有邻接点{if (rmm == 0) break; // 无余量直接退出cur[u] = eg; // 当前弧优化 更新当下次访问该点时从哪条边开始遍历int to = edges[eg].to, w = edges[eg].w;if (w > 0 && dep[to] == dep[u] + 1) // 往层数高的方向增广{int c = dfs(to, min(w, rmn)); // 递归得到该点流量 传递下去的流量是边的容量w与当前流量flow中的较小值rmn -= c; // 剩余流量减少edges[eg].w -= c; // 正向边容量w减去流量cedges[eg ^ 1].w += c; // 反向边容量w加上流量c}}return flow - rmn; // 返回传递的流量的大小
}int dinic()
{int ans = 0; // ans代表总流量while (bfs()) // 只要还可以到达终点就一直bfs下去ans += dfs(start, INF);return ans;
}
Improved Shortest Augumenting Path (ISAP算法)
考虑到Dinic中可能需要bfs多次,ISAP对此做出改进,只需要进行一次bfs即可
首先跑一遍bfs,从汇点到源点处理每个结点的深度
再从源点到汇点跑dfs,和Dinic类似,只是当一个点跑完后,如果从上一个点传过来的流量 flow 比该点的流过的流量 used 大,说明这个点的使用价值已经榨干了,但是还有剩余的流量,则把它的深度加1,如果出现断层(某个深度没有点),结束算法,没出现就一直跑下去
下方代码已加入当前弧优化
struct Edge
{int to, next, w;
};int dep[maxn], gap[maxn]; // dep[i]表示结点i在第几层 gap[i]表示第i层有多少结点
void bfs()
{memset(dep, -1, sizeof(dep));memset(gap, 0, sizeof(gap));dep[end] = 0; // 汇点层数初始化为0gap[0] = 1; // 层数为0的点个数初始化为1queue<int> q;q.push(end); // 汇点入队while (!q.empty()){int u = q.front();q.pop();for (int i = head[u]; i != -1; i = edge[i].next){int to = edge[i].to;if (dep[to] != -1) continue; // 层数不为-1说明已经访问过这个点了dep[to] = dep[u] + 1; // 更新to点层数gap[dep[to]] ++ ; // 更新该层数点的数量 q.push(to); // to点入队}}return;
}int maxflow;
int dfs(int u, int flow) // u表示当前结点 flow表示目前流量
{if (u == end) // 找到汇点{maxflow += flow; // 更新最大流量return flow; // 返回目前的流量}int used = 0; // 从u开始使用的流量for (int i = cur[u]; i != -1; i = edge[i].next){cur[u] = i; // 当前弧优化 更新当下次访问该点时从哪条边开始遍历int to = edge[i].to, w = edge[i].w;if (w > 0 && dep[to] + 1 == dep[u]) // 边还有余量and层数符合要求(注意计算层数的时候是从汇点到源点的){int c = dfs(to, min(w, flow - used)); // 递归得到该点流量 传递下去的流量是边的容量w与当前流量flow-used中的较小值if (c > 0){edge[i].w -= c; // 正向边容量w减去流量cedge[i ^ 1].w += c; // 反向边容量w加上流量cused += c; // 更新已经用过的流量}if (used == flow) return used; // used和flow相等说明已经没有剩余流量分给其他的边了 所以直接返回}}// 如果能到这一步 说明u的所有邻接点都已经遍历过了 且还有剩余流量// 此时我们需要修改u点的层数gap[dep[u]] -- ; // 修改原本层数的结点数if (gap[dep[u]] == 0) dep[start] = n + 1; // 说明没有层数为dep[u]的结点了 断层 不可能再到达汇点了dep[u] ++ ; // 更新u的层数gap[dep[u]] ++ ; // 更新新层数的结点数return used; // 返回流过的流量
}int ISAP()
{maxflow = 0; // maxflow是最大流量bfs();while (dep[start] < n){memcpy(cur, head, sizeof(head));dfs(s, INF);}return maxflow;
}
相关文章:

【图论】网络流
网络流目前只整理模板,学习的话这篇博客可能不太适合 代码参考下方博客,加了一些自己的注释 算法学习笔记(28): 网络流究级的最大流算法:ISAP与HLPP FF 和 EK 仅用作理解代码,赛时请使用 Dinic 或 ISAP 下文建图方式都基于链式…...

【Matplotlib】figure方法 你真的会了吗!?
🎈个人主页:甜美的江 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:matplotlib 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...
[C++]继承(续)
一、基类和派生类对象赋值转换 在public继承时,父类和子类是一个“is - a”的关系。 子类对象赋值给父类对象/父类指针/父类引用,我们认为是天然的,中间不产生临时对象,也叫作父子类赋值兼容规则(切割/切片ÿ…...

恒创科技:服务器内存不足影响大吗?
服务器在为网站、应用程序和在线服务提供支持方面发挥着关键作用。这些服务器需要提供最佳性能,以确保正常无缝的用户体验,而RAM是显著影响服务器性能的关键配置之一。 RAM 是一种随机存取存储器,计算机和服务器使用它来临时存储正在使…...
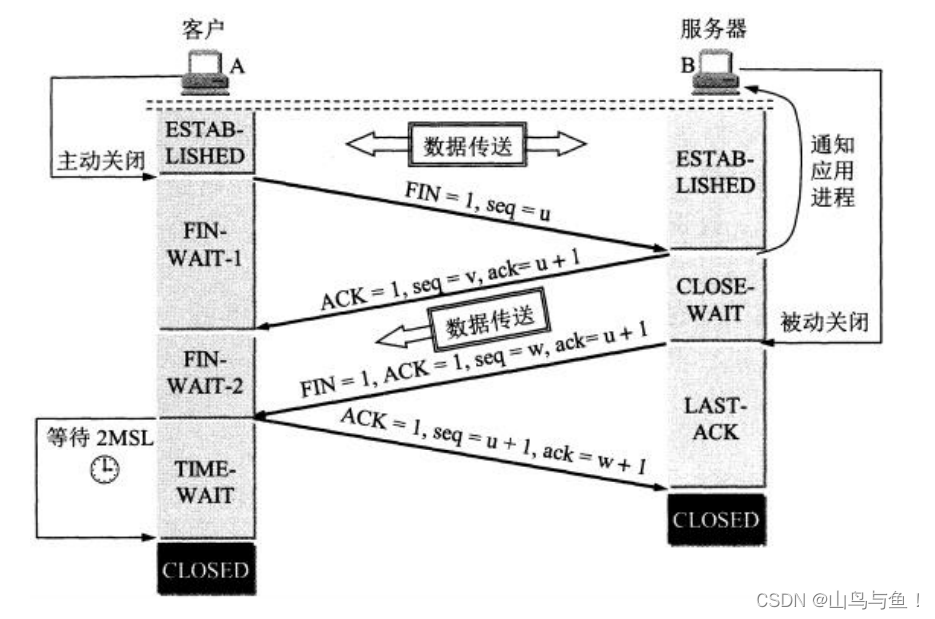
深入理解网络通信和TCP/IP协议
目录 计算机网络是什么? 定义和分类 计算机网络发展简史 计算机网络体系结构 OSI 七层模型 TCP/IP 模型 TCP/IP 协议族 TCP/IP 网络传输中的数据 地址和端口号 MAC地址 IP 地址 端口号 为什么端口号有65535个? 综述 TCP 特性 TCP 三次握…...
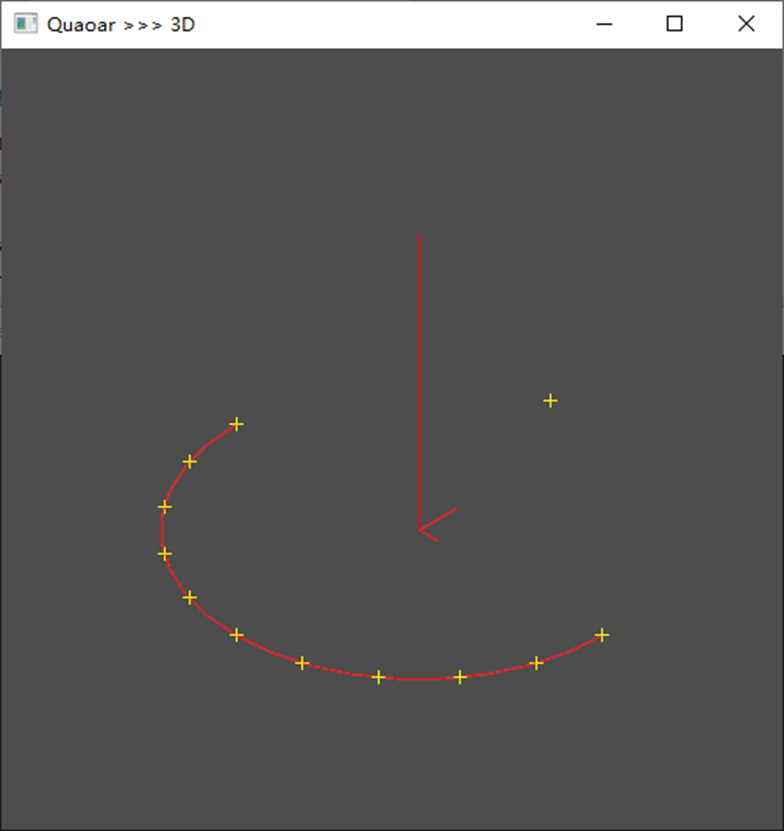
Open CASCADE学习|分割曲线
1、通过参数进行分割 分别获得曲线的 FirstParameter 和 LastParameter ,然后对参数进行分割,获得n个ui,并对每个ui调用D0(获得这个点的坐标值)或D1(获得这个点的坐标值和切向量)。这个方法的优…...
vulhub中Adminer远程文件读取漏洞复现(CVE-2021-43008)
Adminer是一个PHP编写的开源数据库管理工具,支持MySQL、MariaDB、PostgreSQL、SQLite、MS SQL、Oracle、Elasticsearch、MongoDB等数据库。 在其版本1.12.0到4.6.2之间存在一处因为MySQL LOAD DATA LOCAL导致的文件读取漏洞。 参考链接: https://gith…...
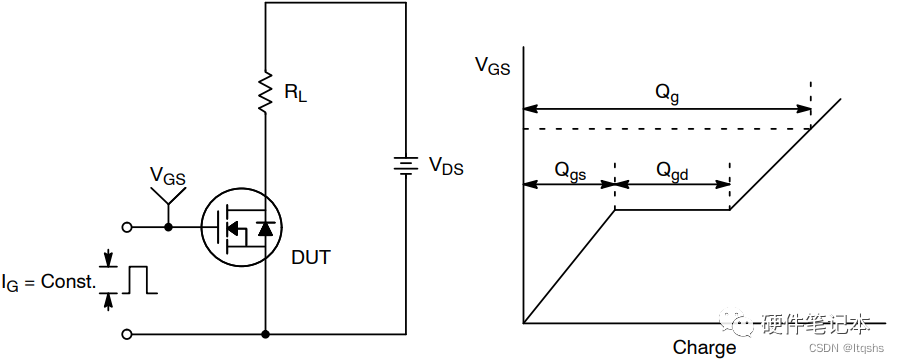
MOS管驱动电流估算-Qg参数
MOS管驱动电流估算 例:FDH45N50F如下参数: 有人可能会这样计算: 开通电流 带入数据得 关断电流 带入数据得 于是乎得出这样的结论,驱动电流只需 250mA左右即可。仔细想想这样计算对吗? 这里必须要注意这样一个条件细…...

Vision Transfomer系列第一节---从0到1的源码实现
本专栏主要是深度学习/自动驾驶相关的源码实现,获取全套代码请参考 这里写目录标题 准备逐步源码实现数据集读取VIt模型搭建hand类别和位置编码类别编码位置编码 blocksheadVIT整体 Runner(参考mmlab)可视化 总结 准备 本博客完成Vision Transfomer(VIT)模型的搭建和flowers数…...
【CSS + ElementUI】更改 el-carousel 指示器样式且隐藏左右箭头
需求 前三条数据以走马灯形式展现,指示器 hover 时可以切换到对应内容 实现 <template><div v-loading"latestLoading"><div class"upload-first" v-show"latestThreeList.length > 0"><el-carousel ind…...

Ubuntu 22.04 上安装和使用 Go
1.下载 All releases - The Go Programming Language //https://golang.google.cn/dl/wget https://golang.google.cn/dl/go1.21.6.linux-amd64.tar.gz 2.在下载目录下执行,现在,使用以下命令将文件提取到 “/usr/local ” 位置 sudo tar -C /usr/…...

ES6-const
一、基本用法 - 语法:const 标识符初始值;注意:const一旦声明变量,就必须立即初始化,不能留到以后赋值 - 规则:1.const 声明一个只读的常量,一旦声明,常量的值就不能改变2.const 其实保证的不是变量的值不…...

Android消息通知Notification
Notification 发送消息接收消息 #前言 最近在做消息通知类Notification的相关业务,利用闲暇时间总结一下。主要分为两部分来记录:发送消息和接收消息。 发送消息 发送消息利用NotificationManager类的notify方法来实现,现用最普通的方式发…...
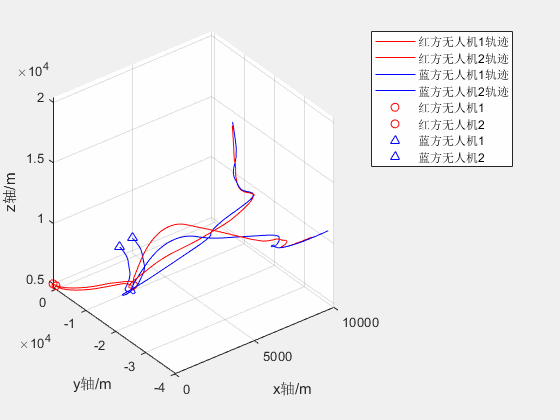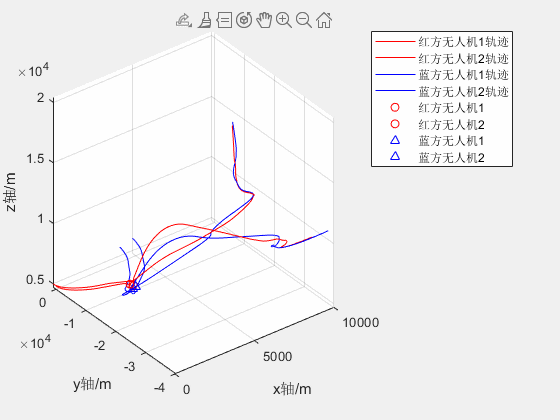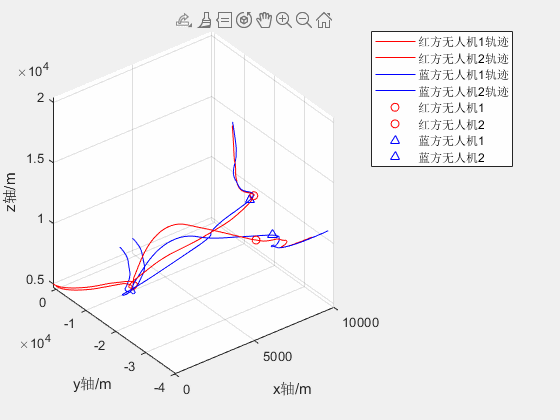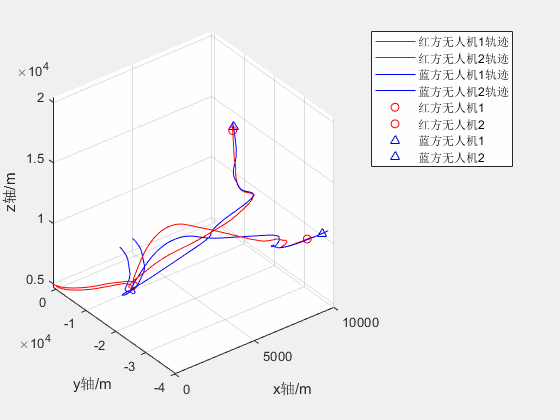
2V2无人机红蓝对抗仿真
两架红方和蓝方无人机分别从不同位置起飞,蓝方无人机跟踪及击毁红方无人机 2020a可正常运行 2V2无人机红蓝对抗仿真资源-CSDN文库...

VUE3语法--computed计算属性中get和set使用案例
1、功能概述 计算属性computed是Vue3中一个响应式的属性,最大的用处是基于多依赖时的监听。也就是属性A的值可以根据其他数据的变化而响应式的变化。 在Vue3中,你可以使用computed函数来定义计算属性。computed函数接收两个参数:一个包含getter和setter函数的对象和可选的…...

Linux cd 和 df 命令执行异常
这篇记录一些奇奇怪怪的命令执行异常的情况,后续有新的发现也会补录进来 情况一 /tmp 目录权限导致 按 tab 补充报错 情况描述 cd 按 tab 自动补充文件报错(普通用户) bash: cannot create temp file for here-document: Permission denie…...
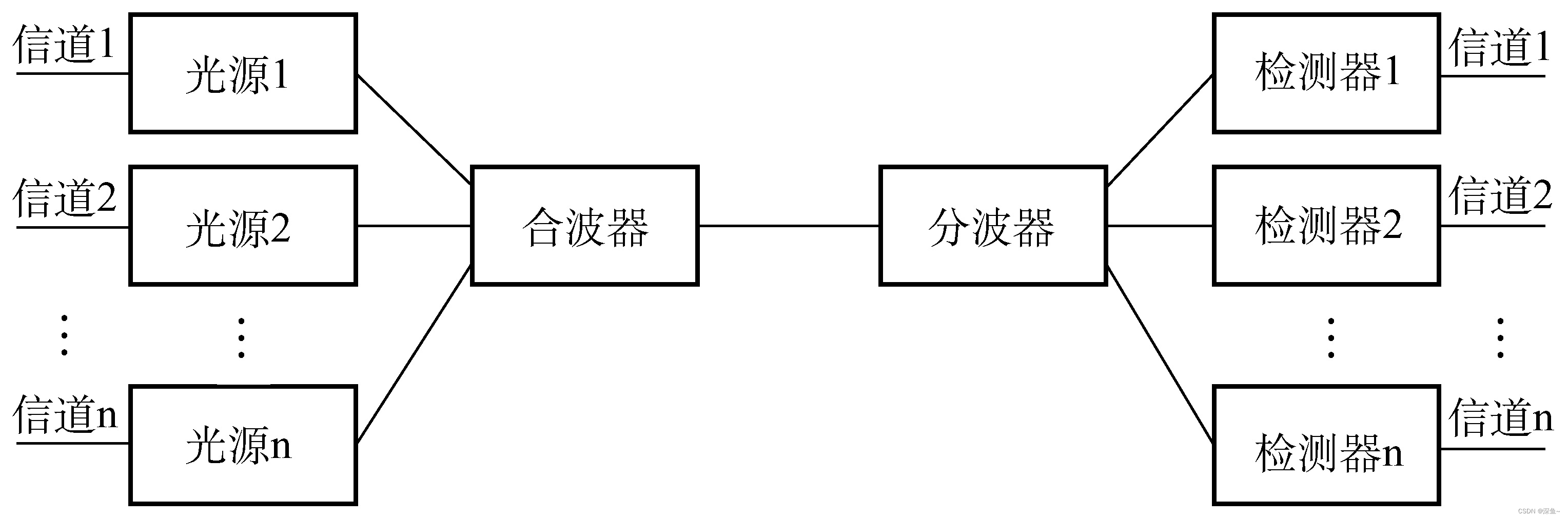
【计算机网络】物理层概述|通信基础|奈氏准则|香农定理|信道复用技术
目录 一、思维导图 二、 物理层概述 1.物理层概述 2.四大特性(巧记"械气功程") 三、通信基础 1.数据通信基础 2.趁热打铁☞习题训练 3.信号の变身:编码与调制 4.极限数据传输率 5.趁热打铁☞习题训练 6.信道复用技术 推荐 前些天发…...
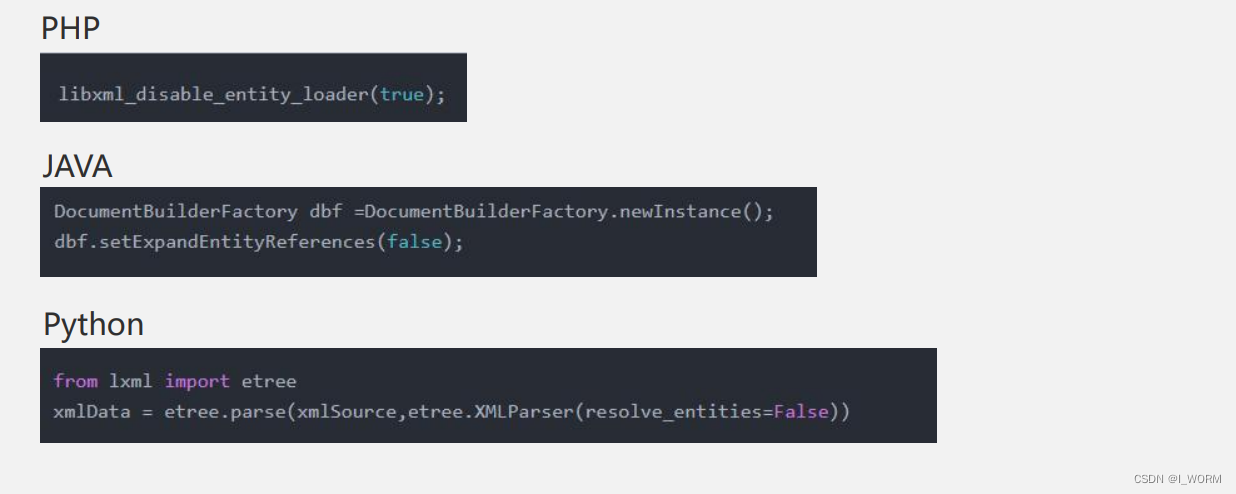
XXE基础知识整理(附加xml基础整理)
全称:XML External Entity 外部实体注入攻击 原理 利用xml进行读取数据时过滤不严导致嵌入了恶意的xml代码;和xss原理雷同 危害 外界攻击者可读取商户服务器上的任意文件; 执行系统命令; 探测内网端口; 攻击内网网站…...

【pytorch】anaconda使用及安装pytorch
https://zhuanlan.zhihu.com/p/348120084 https://blog.csdn.net/weixin_44110563/article/details/123324304 介绍 Conda创建环境相当于创建一个虚拟的空间将这些包都装在这个位置,不需要了可以直接打包放入垃圾箱,同时也可以针对不同程序的运行环境选…...

SpringBoot过滤器获取响应的参数
一、背景 在项目开发过程中,需要对于某些接口统一处理。 这时候就需要获取响应的报文,再对获取的报文进行统一处理。 二、了解过滤器 首先了解一下过滤器拦截器的区别: JAVA中的拦截器、过滤器:https://blog.csdn.net/qq_38254…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
