数据结构与算法:图论(邻接表板子+BFS宽搜、DFS深搜+拓扑排序板子+最小生成树MST的Prim算法、Kruskal算法、Dijkstra算法)
前言
图的难点主要在于图的表达形式非常多,即数据结构实现的形式很多。算法本身不是很难理解。所以建议精通一种数据结构后遇到相关题写个转换数据结构的接口,再套自己的板子。
邻接表板子(图的定义和生成)
public class Graph{public HashMap<Integer,Node>nodes;//点集,第一个参数是点的编号。和Node类中的value一致。不一定是Integer类型的,要看具体的题,有的题点编号为字母。public HashSet<Edge>edges;//边集public Graph(){nodes = new HashMap<>();edges = new HashSet<>();}
}public class Node{public int value;//点的编号,不一定是Integer类型的,要看具体的题,有的题点编号为字母。public int in;//入度public int out;//出度public ArrayList<Node>nexts;//出去的边直接相连的邻居。public ArrayList<Edge>edges//出去的边public Node(int value){this.value=value;in = 0;out = 0;nexts = new ArrayList<>();edges = new ArrayList<>();}
}public class Edge{public int weight;//边上权重public Node from;public Node to;public Edge(int weight,Node from,Node to){this.weight=weight;this.from=from;this.to=to;}
}//现在题目是用三元组来表示图,即给多个三元组{a,b,c},a表示边的起点,b表示边的终点,c表示边的权重。
public static Graph createGraph(Integer[][] matrix){Graph graph = new Graph();for(int i=0;i<matrix.length;i++){Integer from = matrix[0][0];Integer to = matrix[0][1];Integer weight = matrix[0][2];if(!graph.nodes.containsKey(from)){//没有把边的起点加入点集graph.nodes.put(from,new Node(from));}if(!graph.nodes.containsKey(to)){//没有把边的终点加入点集graph.nodes.put(to,new Node(to));}Node fromNode = graph.nodes.get(from);//拿到起点Node toNode = graph.nodes.get(to);//拿到终点Edge newEdge = new Edge(weight,fromNode,toNode);//构造边graph.edges.add(newEdge);fromNode.nexts.add(toNode);fromNode.edges.add(newEdge);fromNode.out++;toNode.in++;}return graph;
}
BFS、DFS板子
图和二叉树的宽搜最大的不同的就是,图是可能有环的。二叉树是没环的,所以图可能死循环卡住,所以需要额外记录是否有访问过,一般是哈希表或者数组。
深搜是点入栈之前就需要处理了,广搜是点入队列之后开始处理。
public static void bfs(Node node){if(node==null) return;Queue<Node> queue = new LinkedList<>();HashSet<Node> set = new HashSet<>();queue.add(node);set.add(node);while(!queue.isEmpty()){Node cur = queue.poll();/* 具体的处理逻辑(宽搜一般是结点入队列后再处理)*/for(Node next: cur.nexts){if(!set.contains(next)){//如果set中没有,那么说明这个next结点没有被访问过queue.add(next);//扔到队列里set.add(next);//并且标记访问}}}
}public static void dfs(Node node){if(node==null) return;Stack<Node> stack = new Stack<>();HashSet<Node> set = new HashSet<>();stack.add(node);set.add(node);/*具体的处理逻辑(深搜一般是结点入栈前就进行处理)*/while(!stack.isEmpty()){Node cur = stack.pop();for(Node next:cur.nexts){if(!set.contains(next)){stack.push(cur);//在这里需要把cur和next两个结点同时入栈是因为stack.push(next);//想在栈里保持深度搜索的路径。这次搜索相比于上一次搜索,在栈中就多了一个next结点。set.add(cur);set.add(next);/*具体的处理逻辑 */break;//之所以立马break是因为深搜每次只走一步,不像宽搜每次走一层。}}}
}
深拷贝实现(dfs+bfs实现)
见本人另一篇博客http://t.csdnimg.cn/LgIZp
拓扑排序
因为拓扑排序是一定没有环的,那么就一定存在至少一个入度为0的点,我们将这个(些)点放入队列。以这个(其中一个)点为起点出发。每次删掉该点出度相连的直接边,那么就肯定会有新的入度为0的点产生,然后放入队列。那么入队的顺序就是拓扑排序的顺序。
public static List<Node> top(Graph graph){HashMap<Node,Integer> inMap = new HashMap<>();//Node为某一个结点,Integer为该结点剩余的入度Queue<Node> zeroInQueue = new LinkedList<>();//专门存放入度为0的结点的队列。for(Node node: graph.nodes.values()){inMap.put(node, node.in);if(node.in==0) zeroInQueue.add(node);}//第一次循环后,找出了所有入度为0的点放入了队列。List<Node> result = new ArrayList<>();while(!zeroInQueue.isEmpty()){Node cur = zeroInQueue.poll();result.add(cur);for(Node next:cur.nexts){int newin = inMap.get(next)-1;//注意不是next.in-1,因为graph中的入度是不更新的,只有inMap的入度是更新的inMap.push(next,newin);if(newin==0) zeroInQueue.add(next);}}return result;
}
自己留档用
public static void top(Graph graph){if(graph.nodes==null) return null;Queue<Node>queue = new LinkedList<>();for(Node node:graph.nodes.values()){if(node.from==0){//找到入度为0的点/*具体的处理逻辑*/queue.add(node);}}while(!queue.isEmpty()){Node cur = queue.poll();for(Node next:cur.nexts){next.in--;}for(Node node:graph.nodes.values()){if(node.from==0){queue.add(node);}}}
}最小生成树MST
生成树的定义:
一个连通图的生成树是一个极小的连通子图,它包含图中全部的n个顶点,但只有构成一棵树的n-1条边。
生成树的属性:
- 一个连通图可以有多个生成树;
- 一个连通图的所有生成树都包含相同的顶点个数和边数;
- 生成树当中不存在环;
- 移除生成树中的任意一条边都会导致图的不连通;
- 在生成树中添加一条边会构成环。
- 对于包含n个顶点的连通图,生成树包含n个顶点和n-1条边;
- 对于包含n个顶点的无向完全图最多包含 n(n−2)棵生成树。
最小生成树的定义:
所谓一个带权图的最小生成树,就是指原图中边的权值之和最小的生成树。即,最小生成树是和带权图联系在一起的;如果仅仅只是非带权的图,只存在生成树。
Prim算法
适合无向图。
Prim算法的时间复杂度为O(n^2),其中n为顶点数。
可以去看看B站懒猫老师的这部分讲解,个人感觉除了表达为了严谨,用了比较多复杂的数学符号,其他都是讲的很好的。https://www.bilibili.com/video/BV1Ua4y1i7tf/
public static class EdgeComparator implements Comparator<Edge>{@Overridepublic int compare(Edge o1, Edge o2){return o1.weight - o2.weight;}
}public static Set<Edge> prim(Graph graph){//1.选择一个不在set里的起始点,加入set,且解锁该点相连的边//2.选择权值最小的边,看终点是否在set里//3.如果不在,说明是新的点,不会构成环,则该点放入结果集和set中,从该点的相连边开始遍历//4.如果在,说明不是新的点,跳过该点PriorityQueue<Edge> queue = new PriorityQueue<>(new EdgeComparator());//存储边的小根堆,即优先队列Set<Edge> result = new HashSet<>();//存储结果HasSet<Node> set = new HashSet<>();//用来判断是否是新的点 /*为了避免该图是多个不连通的子图组合而成的,然后题目让我们求最小生成森林,所以需要遍历,如果确定是只有一个连通子图,那么可以去掉循环,可以见待会展示的图。1.随便选择一个起始点,加入set,解锁该点相连的边*/for(Node node:graph.nodes.values()){if(!set.contains(node)){set.add(node);for(Edge edge:node.edges){queue.add(edge);}while(!queue.isEmpty()){Edge edge = queue.poll();Node toNode = edge.to;//2.选择权值最小的边,看终点是否在set里if(!set.contains(toNode)){//3.如果不在,说明是新的点,不会构成环,则该点放入结果集和set中,从该点的相连边开始遍历set.add(toNode);result.add(edge);for(Edge edge:toNode.edges){queue.add(edge);}}}}}
}
注意点1:最小生成森林
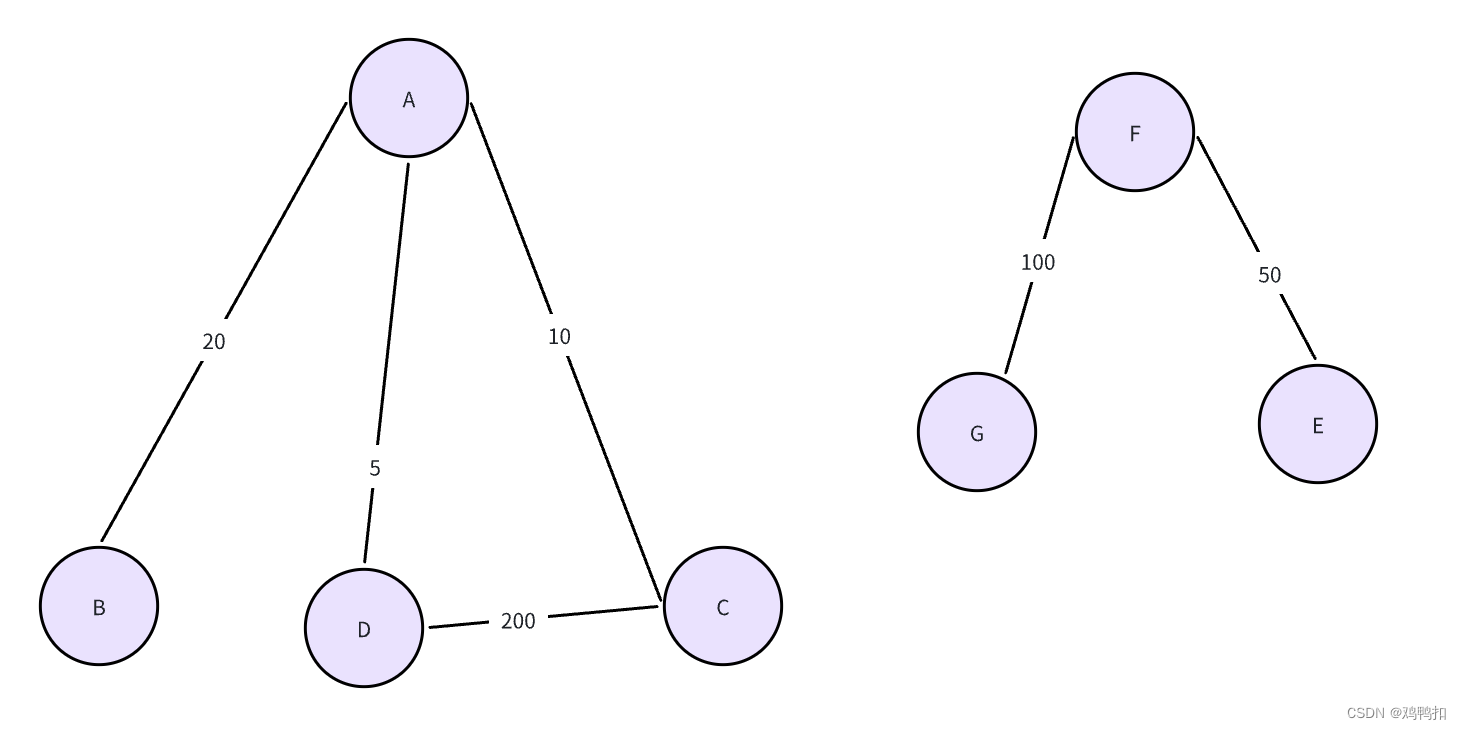
像是如上图片,A到G的七个点一共是一个大图,但是左边的A到D算是一个子图,右边的E到G算是一个子图。这两个子图之间是相互不连通的。那么我们如果要想得到这个大图的最小生成森林,也是互相不连通的两部分组成的,如下:
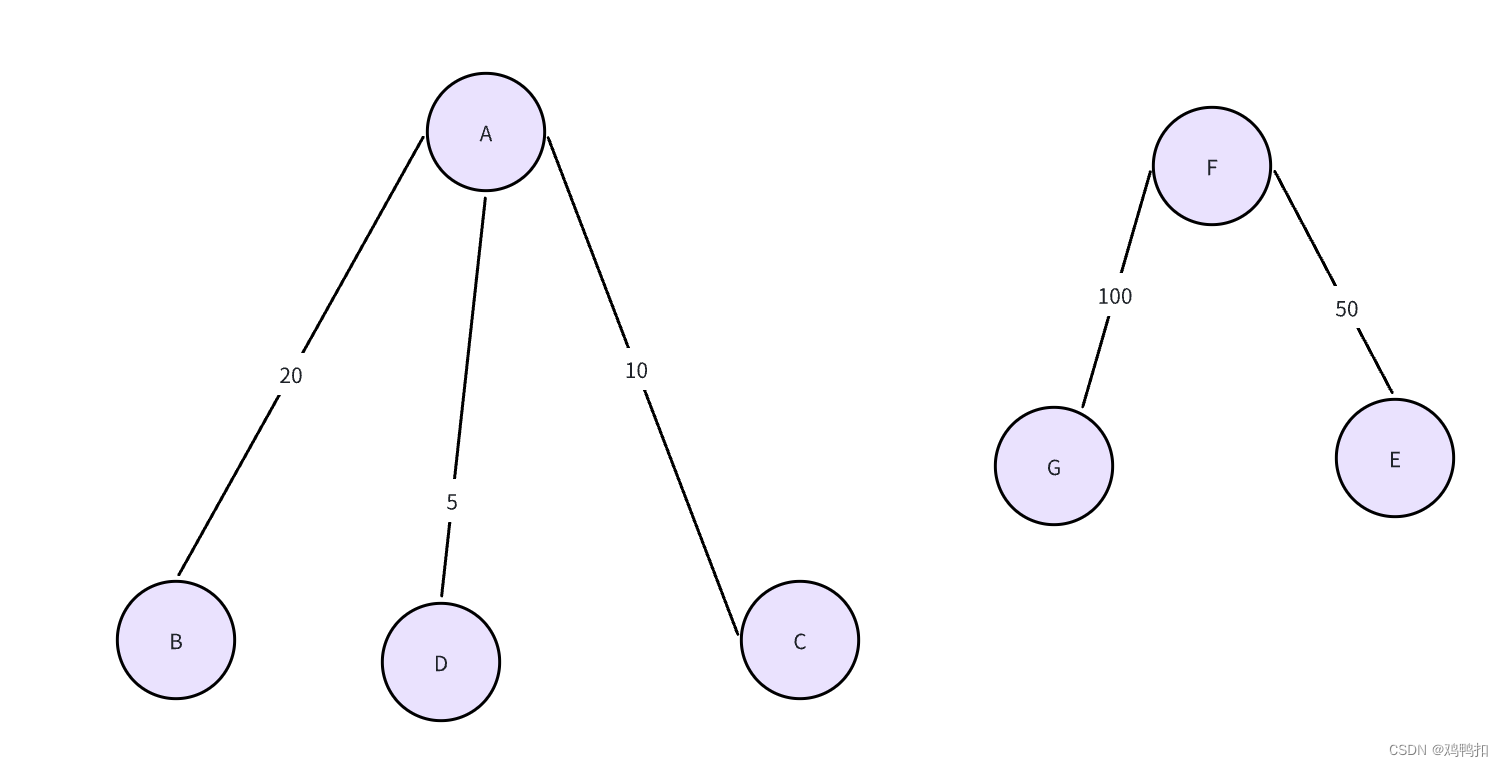
那么此时我们就需要一个外层循环来确保遍历到所有子图。
相关题
P3366 【模板】最小生成树
https://www.luogu.com.cn/problem/P3366
Kruskal算法
适合有向无环图。
板子
public static class EdgeComparator implements Comparator<Edge>{@Overridepublic int compare(Edge o1, Edge o2){return o1.weight - o2.weight;}
}public static Set<Edge> kruskal(Graph graph){//1.将每个点作为一个单独的集合//2.将边按照权值从小到大排序//3.依次遍历边,判断起点和终点的集合是否是一个集合//4.如果不是一个集合,将起点和终点的集合合并为一个集合//5.如果是一个集合,说明会构成环,则跳过这条边和边的起点和终点UnionFind unionFind = new UnionFind();//1.unionFind.makeSets(graph.nodes.values());//2.PriorityQueue<Edge> queue = new PriorityQueue<>(new EdgeComparator());for(Edge edge: graph.edges){queue.add(edge);}Set<Edge> result = new HashSet<>();while(!queue.isEmpty()){Edge edge = queue.poll();if(!unionFind.isSameSet(edge.from, edge.to)){result.add(edge);unionFind.union(edge.from, edge.to);}}return result;
}相关题
P3366 【模板】最小生成树 https://www.luogu.com.cn/problem/P3366
P2872 [USACO07DEC]Building Roads https://www.luogu.com.cn/problem/P2872
P1546 [USACO3.1]最短网络 Agri-Net https://www.luogu.com.cn/problem/P1546
Dijkstra算法
适用于没有累加后权值为负数的环的图(也可以直接粗暴地大范围地认为权值为负数的图不适合)
感觉这里左神没有讲的很好,可以去看b站懒猫老师讲的。
板子
初代板子找寻距离最短的且没有被遍历到的节点的函数是通过循环实现的,复杂度较高。但是可以用堆优化,不过不是系统提供的堆算法,因为系统提供的堆不支持给过的节点的值修改的操作,所以需要自己手写实现堆。
public static HashMap<Node, Integer> Dijkstra(Node head){HashMap<Node,Integer>distanceMap = new HashMap<>();//从head点出发,到达每个节点的最短距离(包含head自身)HashSet<Node> set = new HashSet<>();//节点是否已经遍历过distanceMap.put(head,0);Node minNode = selectNode(distanceMap, set);while(minNode!=null){int mindistance = distanceMap.get(minNode);//当前从head出发,到达最近点的最短距离for(Edge edge:minNode.edges){//最近点的邻边Node toNode = edge.to;//最近点直接相连的节点if(!distanceMap.containsKey(toNode))//如果这个最近点直接相连的节点没有在distanceMap中出现过//那么说明这条最近点的邻边是新遍历到的边distanceMap.put(toNode,mindistance+edge.weight);//我们需要把这条新边的新点距离head的距离加入distanceMap中else{ distanceMap.put(edge.to,Math.min(distanceMap.get(toNode),mindistance+edge.weight))}//如果这个节点不是新遍历到的,那么就需要看是否需要更新我们之前的最短距离}set.add(minNode);minNode = selectNode(distanceMap, set);}return distanceMap;
}public static Node selectNode(HashMap<Node,Integer> distanceMap, HashSet<Node> set){int minDistance = Integer.MAX_VALUE;Node minNode = null;//将distanceMap中每个节点拿出来,找出距离最短的且没有被遍历到的节点for(Entry<Node,Integer> entry: distanceMap.entrySet()){Node node = entry.getKey();int distance = entry.getValue();if(!set.containsKey(node)&&distance<minDistance){minDistance = distance;minNode = node;}}return minNode;
}
相关文章:

数据结构与算法:图论(邻接表板子+BFS宽搜、DFS深搜+拓扑排序板子+最小生成树MST的Prim算法、Kruskal算法、Dijkstra算法)
前言 图的难点主要在于图的表达形式非常多,即数据结构实现的形式很多。算法本身不是很难理解。所以建议精通一种数据结构后遇到相关题写个转换数据结构的接口,再套自己的板子。 邻接表板子(图的定义和生成) public class Graph…...

Python之PySpark简单应用
文章目录 一、介绍1.准备工作2. 创建SparkSession对象:3. 读取数据:4. 数据处理与分析:5. 停止SparkSession: 二、示例1.读取解析csv数据2.解析计算序列数据map\flatmap 三、问题总结1.代码问题2.配置问题 一、介绍 PySpark是Apa…...
降维(Dimensionality Reduction)
一、动机一:数据压缩 这节我将开始谈论第二种类型的无监督学习问题,称为降维。有几个原因使我们可能想要做降维,其一是数据压缩,它不仅允许我们压缩数据使用较少的计算机内存或磁盘空间,而且它可以加快我们的学习算法。…...
怎样调用浏览器插件(如metamask小狐狸钱包))
web应用(网页)怎样调用浏览器插件(如metamask小狐狸钱包)
下边是与gpt的对话,代码可以在浏览器控制台验证 一,在网页上点击一个连接按钮 然后小狐狸钱包就打开了,是怎么实现的呢 当你在网页上点击一个连接按钮,然后自动打开MetaMask(通常被称为“小狐狸钱包”,一种…...
2024美赛数学建模C题完整论文教学(含十几个处理后数据表格及python代码)
大家好呀,从发布赛题一直到现在,总算完成了数学建模美赛本次C题目Momentum in Tennis完整的成品论文。 本论文可以保证原创,保证高质量。绝不是随便引用一大堆模型和代码复制粘贴进来完全没有应用糊弄人的垃圾半成品论文。 C论文共49页&…...
Matplotlib绘制炫酷柱状图的艺术与技巧【第60篇—python:Matplotlib绘制柱状图】
文章目录 Matplotlib绘制炫酷柱状图的艺术与技巧1. 簇状柱状图2. 堆积柱状图3. 横向柱状图4. 百分比柱状图5. 3D柱状图6. 堆积横向柱状图7. 多系列百分比柱状图8. 3D堆积柱状图9. 带有误差线的柱状图10. 分组百分比柱状图11. 水平堆积柱状图12. 多面板柱状图13. 自定义颜色和样…...

window 挂载linux 网盘
背景:因为很多情况下,作为开发人员,我们都希望用Linux的编译环境,但是可以用windows下各种IDE来写code; linux 服务器安装NFS服务 说明:NFS 服务就是让不同的计算机可以在不同的操作系统之间共享文件,采用的就是服务端/客户端的架构,在NFS服务器上将目录设置为输出目录(…...

windows10忘记密码的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
进程和线程的区别详解
🎥 个人主页:Dikz12📕格言:那些在暗处执拗生长的花,终有一日会馥郁传香欢迎大家👍点赞✍评论⭐收藏 目录 进程 进程在系统中是如何管理的 进一步认识PCB 线程 能否一直增加线程数目来提高效率 进程和线程…...

(基于xml配置Aop)学习Spring的第十五天
一 . Spring Aop编程简介 再详细点 , 如下 二 . 基于xml配置Aop 解决proxy相关问题 解决问题开始用xml配置AOP 导入pom坐标 <dependency><groupId>org.aspectj</groupId><artifactId>aspectjweaver</artifactId><version>1.9.6</vers…...

Centos7环境安装PHP8
一、安装必要的模块 yum install -y bzip2-devel libcurl-devel libxml2-devel sqlite-devel oniguruma oniguruma-devel libxml2 libxml2-devel bzip2 bzip2-devel libcurl libcurl-devel libjpeg libjpeg-devel zstd libzstd-devel curl libcurl-devel libpng libpng-devel …...
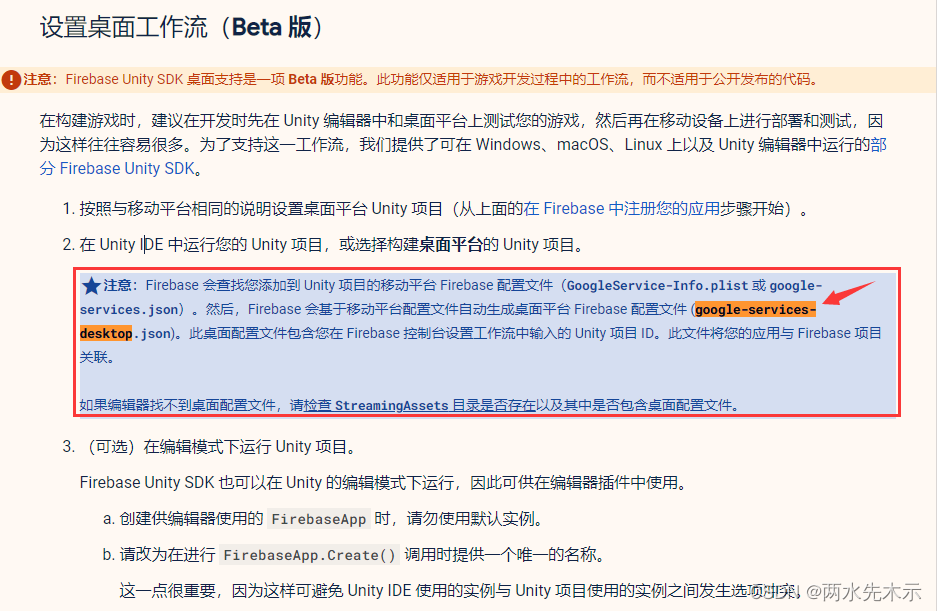
No matching client found for package name ‘com.unity3d.player‘
2024年2月5日更新 必须使用Unity方式接入Unity项目!一句话解决所有问题。(真的别玩Android方式) 大致这问题出现原因是我在Unity采用了Android方式接入Firebase,而Android接入实际上和Unity接入方式有配置上的不一样,我…...
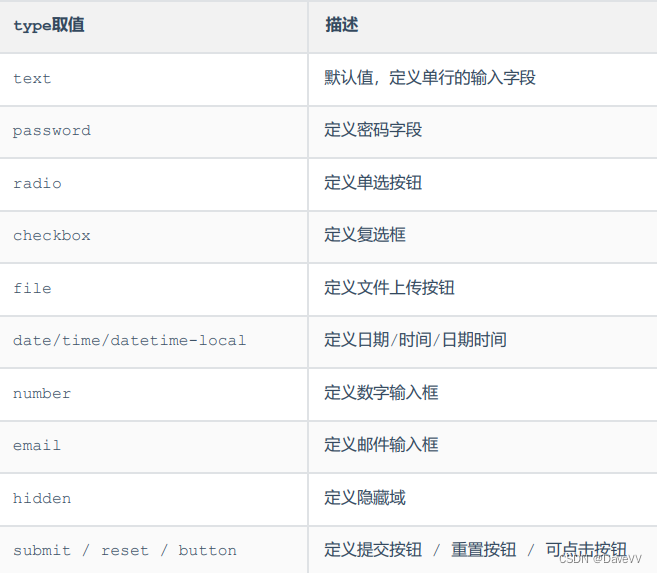
JavaWeb之HTML-CSS --黑马笔记
什么是HTML ? 标记语言:由标签构成的语言。 注意:HTML标签都是预定义好的,HTML代码直接在浏览器中运行,HTML标签由浏览器解析。 什么是CSS ? 开发工具 VS Code --安装文档和安装包都在网盘中 链接:https://p…...
logback日志配置
springboot默认使用logback 无需额外添加pom依赖 1.指定日志文件路径 当前项目路径 testlog文件夹下 linux会在项目jar包同级目录 <property name"log.path" value"./testlog" /> 如果是下面这样配置的话 window会保存在当前项目所在盘的home文件夹…...
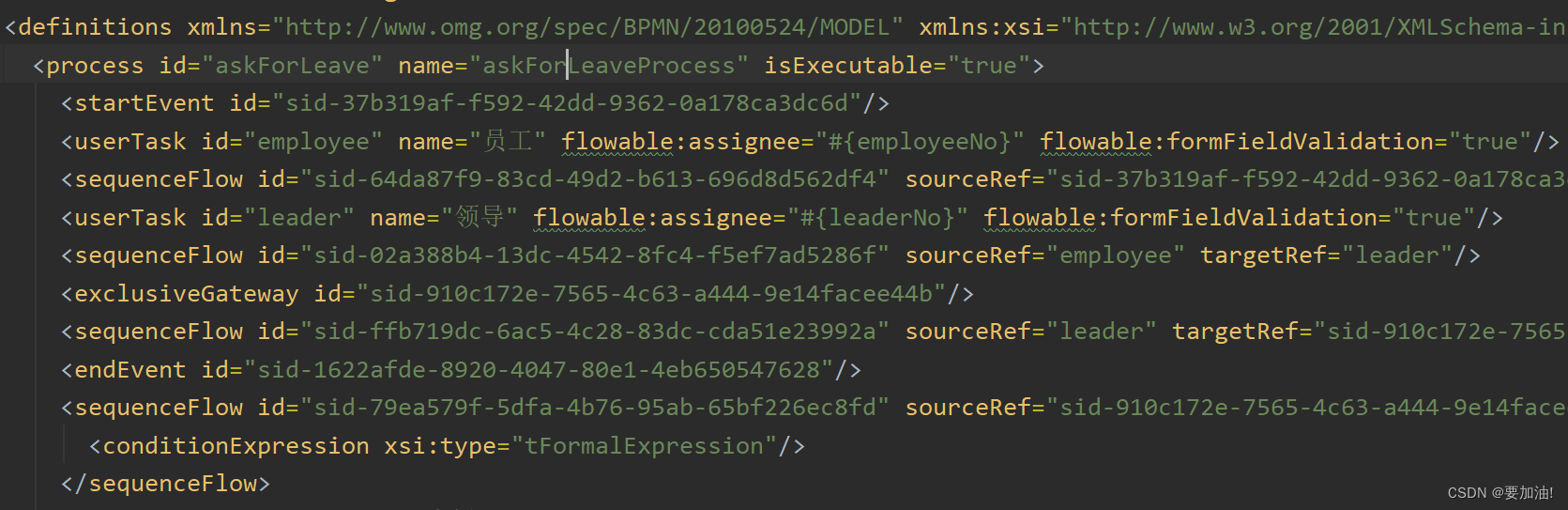
SpringBoot集成Flowable工作流
文章目录 一、了解Flowable1. 什么是Flowable2. Flowable基本流程3. Flowable主要几张表介绍 二、SpringBoot集成Flowable1. 在idea中安装Flowable插件2. SpringBoot集成Flowable3. SpringBoot集成Flowable前端页面 三、创建流程模版(以请假为例) 提示:以下是本篇文…...

try-with-resources 语法详解
目录 一、介绍 二、用法对比 三、优势 四、原理分析 一、介绍 在Java 7中,引入了一项重要的语法糖——try-with-resources,这项特性的目的是为了更有效地处理资源的管理。资源指的是需要在代码执行完毕后手动关闭的对象,比如文件流、网络…...

【Java程序设计】【C00207】基于(JavaWeb+SSM)的宠物领养管理系统(论文+PPT)
基于(JavaWebSSM)的宠物领养管理系统(论文PPT) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于ssm的宠物领养系统 本系统分为前台系统、管理员、收养者和寄养者4个功能模块。 前台系统:游客打开系统…...

2024-2-4-复习作业
源代码: #include <stdio.h> #include <stdlib.h> typedef int datatype; typedef struct Node {datatype data;struct Node *next;struct Node *prev; }*DoubleLinkList;DoubleLinkList create() {DoubleLinkList s(DoubleLinkList)malloc(sizeof(st…...
【Linux】解决:为什么重复创建同一个【进程pid会变化,而ppid父进程id不变?】
前言 大家好吖,欢迎来到 YY 滴Linux 系列 ,热烈欢迎! 本章主要内容面向接触过Linux的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! YY的《C》专栏YY的《C11》专栏YY的…...

【亿级数据专题】「高并发架构」盘点本年度探索对外服务的百万请求量的API网关设计实现
盘点本年度探索对外服务的百万请求量的API网关设计实现 背景介绍高性能API网关API网关架构优化多级缓存架构设计多级缓存富客户端漏斗模型数据读取架构 异步刷新过期缓存网关异步化调用模型高性能批量API调用(减少对于网关的交互和通信)并行调用和请求合…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
