C++枚举算法(3)
我家的门牌号
题目描述: 我家住在一条短胡同里,这条胡同的门牌号从1开始顺序编号。 若所有的门牌号之和减去我家门牌号的两倍,恰好等于n,求 我家的门牌号及总共有多少家。 数据保证有唯一解。 输入 一个正整数n。n < 100000。 输出 一行,包含两个正整数,分别是我家的门牌号及总共有多少 家,中间用单个空格隔开。
样例输入
100
样例输出
10 15
#include<bits/stdc++.h>
using namespace std;
int w(int);
int main()
{int n;cin>>n;for(int i=1;true/*因为题目里没说到底最多有多少家,所以直接true*/;i++){for(int j=1;j<=n;j++){if(w(i)-j*2==n){cout<<j<<" "<<i;//j是我家的门牌号,i是共有多少户 return 0;}}}return 0;
}
int w(int a)
{int sum=0;for(int i=1;i<=a;i++){sum=sum+i;}return sum;
}不定方程求解
题目描述: 给定正整数a,b,c。求不定方程 ax+by=c 关于未知数x和y的所有非负整数解组数。 输入 一行,包含三个正整数a,b,c,两个整数之间用单个空格隔开。每个数均不大于1000。 输出 一个整数,即不定方程的非负整数解组数。
样例输入
2 3 18
样例输出
4
#include<bits/stdc++.h>
using namespace std;
int main()
{int a,b,c;cin>>a>>b>>c;int cnt=0;//用来计算不定方程解的组数 for(int x=0;x<=1000;x++){for(int y=0;y<=1000;y++){if(a*x+b*y==c){cnt++;}}}cout<<cnt; return 0;
}相关文章:
)
C++枚举算法(3)
我家的门牌号 题目描述: 我家住在一条短胡同里,这条胡同的门牌号从1开始顺序编号。 若所有的门牌号之和减去我家门牌号的两倍,恰好等于n,求 我家的门牌号及总共有多少家。 数据保证有唯一解。 输入 一个正整数n。n < 100000。…...
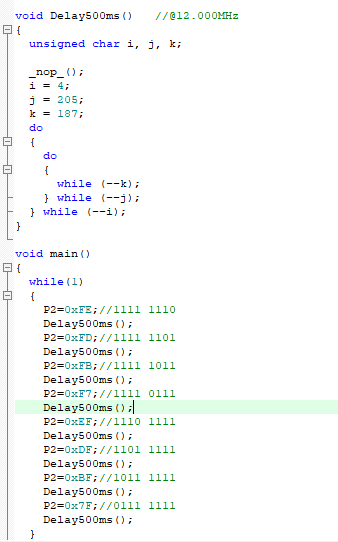
【51单片机】LED的三个基本项目(LED点亮&LED闪烁&LED流水灯)(3)
前言 大家好吖,欢迎来到 YY 滴单片机系列 ,热烈欢迎! 本章主要内容面向接触过单片机的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! YY的《C》专栏YY的《C11》专栏YY的…...

Day 17------C语言收尾之链表的删除、位运算、预处理、宏定义
链表 空链表: 注意:函数不能返回局部变量的地址 操作: 1.创建空链表 2.头插 3.尾插 4.链表遍历 5.链表的长度 free:释放 删除: 头删 void popFront(struct Node *head) { //1.p指针变量指向首节点 //2.断…...
python_蓝桥杯刷题记录_笔记_全AC代码_入门5
前言 关于入门地刷题到现在就结束了。 题单目录 1.P1579 哥德巴赫猜想(升级版) 2.P1426 小鱼会有危险吗 1.P1579 哥德巴赫猜想(升级版) 一开始写的代码是三重循环,结果提交上去一堆地TLE,然后我就给减少…...

二叉树的详解
二叉树 【本节目标】 掌握树的基本概念掌握二叉树概念及特性掌握二叉树的基本操作完成二叉树相关的面试题练习 树型结构(了解) 概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。…...

【第三十五节】idea项目的创建以及setting和Project Structure的设置
项目创建 Project Structure的设置 点击file ~ Project Structure 进入...

【c++】跟webrtc学引用计数
rtc::RefCountInterface 接口类 G:\CDN\rtcCli\m98\src\rtc_base\ref_count.h引用计数想形成一种树状结构 // Interfaces where refcounting is part of the public api should // inherit this abstract interface. The implementation of these // methods is usually provid…...
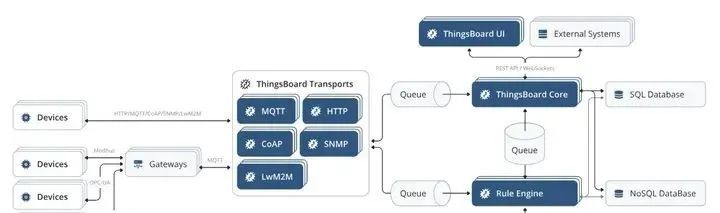
开源免费的物联网网关 IoT Gateway
1. 概述 物联网网关,也被称为IOT网关,是一种至关重要的网络设备。在物联网系统中,它承担着连接和控制各种设备的重要任务,将这些设备有效地连接到云端、本地服务器或其他设备上。它既能够在广域范围内实现互联,也能在…...

华为OD机试真题C卷-篇3
文章目录 查找一个有向网络的头节点和尾节点幼儿园篮球游戏 查找一个有向网络的头节点和尾节点 在一个有向图中,有向边用两个整数表示,第一个整数表示起始节点,第二个整数表示终止节点;图中只有一个头节点,一个或者多…...

[SWPUCTF 2021 新生赛]include
他让我们传入一个flag值 我们传入即可看到代码部分 传入一个php的伪类即可 得到经过Base64加密的flag,解密即可...
LeetCode、17. 电话号码的字母组合【中等,dfs回溯】
文章目录 前言LeetCode、17. 电话号码的字母组合【中等,dfs回溯】题目与类型思路递归回溯优化:StringBuilder来回溯补充代码:2024.1.31(简化) 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博…...
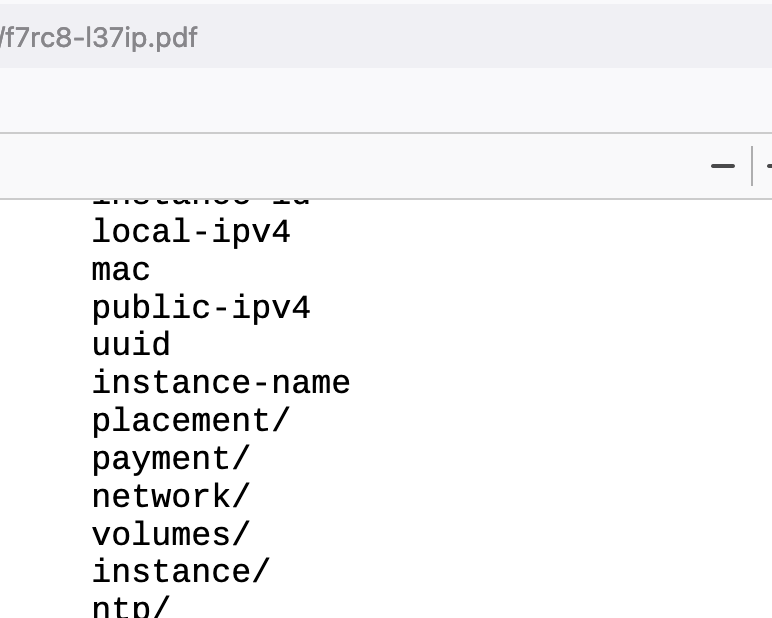
SSRF漏洞给云服务元数据带来的安全威胁
文章目录 前言元数据服务威胁1.1 Metadata元数据1.2 RAM资源管理角色1.3 STS 临时凭据利用1.4 CF云环境利用框架1.5 元数据安全性增强 TerraformGoat2.1 永久性AccessKey2.2 SSRF靶场环境搭建2.3 腾讯云CVM配角色2.4 接管腾讯云控制台 SSRF组合拳案例3.1 上传图片功能SSRF3.2 文…...

【C++】强制类型转换
强制类型转换分为显式和隐式 显式直接用小括号强制转换,float b (int)a; 隐式直接 float b 0.5; int a b; C中更推荐用四个强制类型转换的关键字: 1、static_cast, 2、const_cast, 3、reinterpret_cast, 4、dynami…...
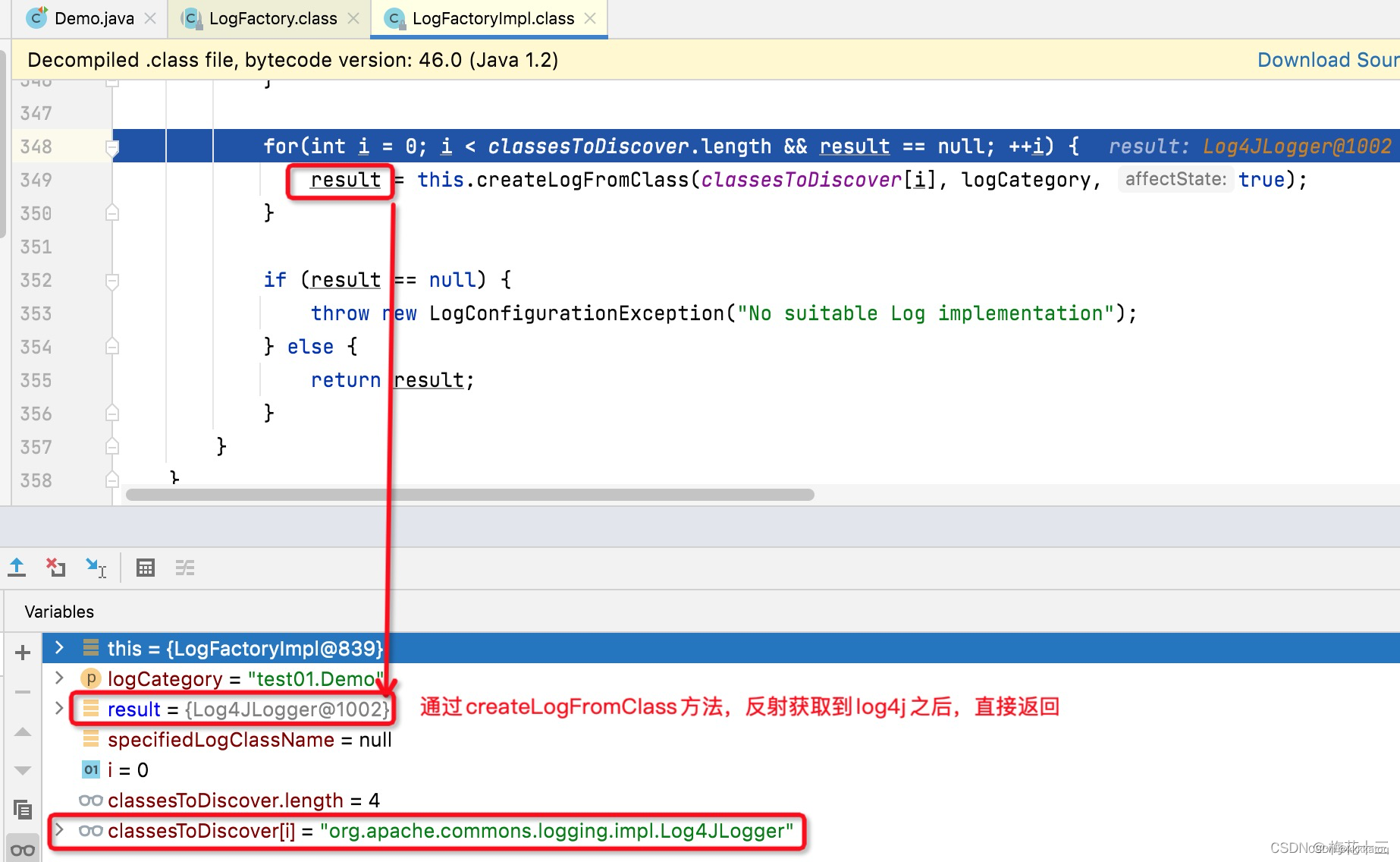
java日志框架总结(四 、JCL日志门面技术)
日志框架出现的历史顺序:Log4j → JUL → JCL → slf4j → logback → log4j2 一、背景 在前面博文中,我们分别讲述了常用的2个日志框架:JUL(Java Util Logging)、Log4J。那么如何选择使用哪一个呢? 根据项…...
mfc140.dll丢失的几种修复方式,有效的解决文件丢失问题
mfc140.dll是Microsoft Foundation Class (MFC)库中的一个非常重要的DLL文件。它承载了许多被执行程序使用的函数和资源。这个库主要被广泛应用于开发Windows操作系统上的应用程序。然而,有时候我们可能会遭遇到mfc140.dll缺失或损坏的情况,这会导致依赖…...
从一个小故事讲解观察者模式~
定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都得到通知并被自动更新。 什么是观察者模式? 观察者模式在我们的日常生活中极其常见。 先来看看观察者模式的定义: 观察者模式定义了对象之间…...
LeetCode、1137. 第 N 个泰波那契数【简单,动态规划】
文章目录 前言LeetCode、1137. 第 N 个泰波那契数【简单,动态规划】题目与分类思路一维动态规划 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博客专家、Java领域优质创作者,博客之星、阿里云平台优质作者、专注于Java后端技术…...
Python爬虫urllib详解
前言 学习爬虫,最初的操作便是模拟浏览器向服务器发出请求,那么我们需要从哪个地方做起呢?请求需要我们自己来构造吗?需要关心请求这个数据结构的实现吗?需要了解 HTTP、TCP、IP 层的网络传输通信吗?需要知…...
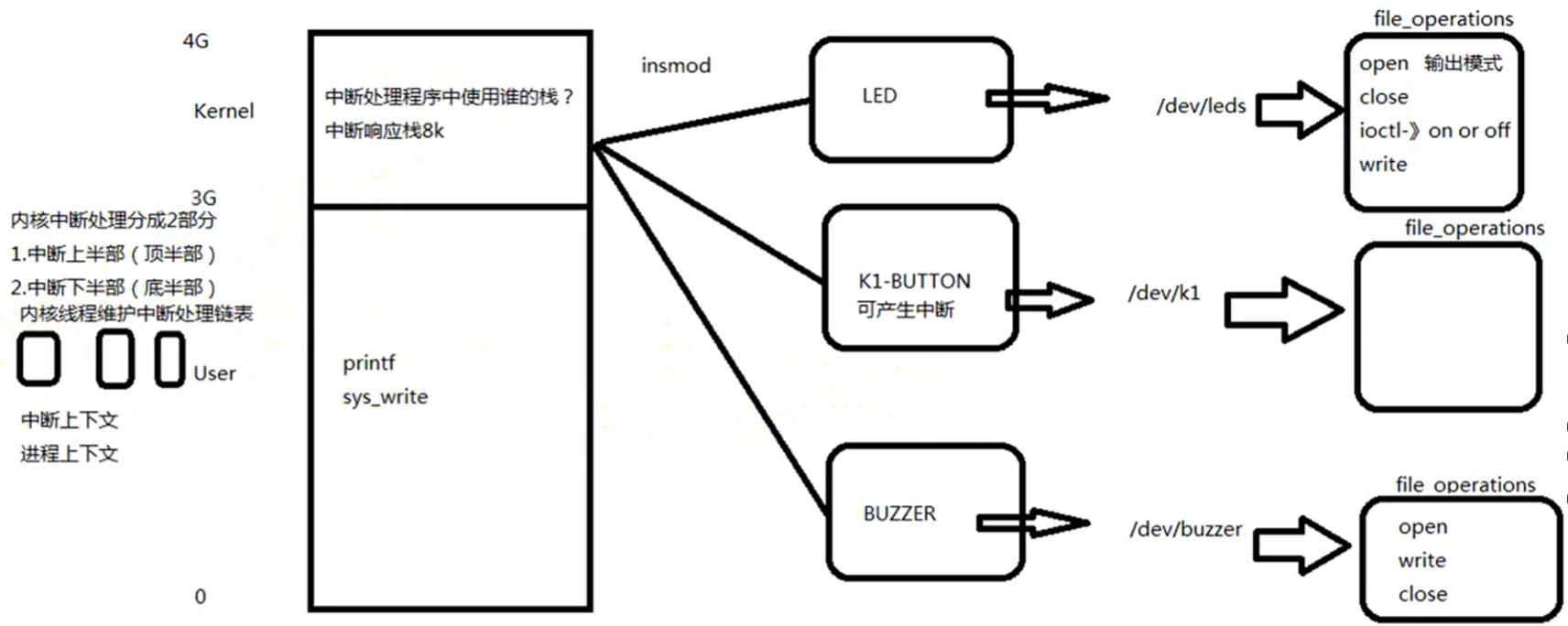
Linux嵌入式开发+驱动开发-中断
swi汇编指令可以产生软中断,以下是硬件中断的产生到执行完毕的全过程: 在自己设计的芯片“CPU响应中断”程序的第四个步骤可以转向“中断向量控制器”,中断向量控制器中存储中断元服务地址即处理中断处理程序的地址,而不用使用0X1…...

android tv开发-1,leanback
目录 1.leanback库的一些事 2.leanback在使用时遇到的一些麻烦 视频卡片 页面空白 关于左侧菜单的一些设置 数据加载异常与加载中的一些操作 如果页面无数据,如何显示错误的页面....
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
