数学建模:数据相关性分析(Pearson和 Spearman相关系数)含python实现
相关性分析是一种用于衡量两个或多个变量之间关系密切程度的方法。相关性分析通常用于探索变量之间的关系,以及预测一个变量如何随着另一个变量的变化而变化。在数学建模中,这是常用的数据分析手段。
相关性分析的结果通常用相关系数来表示,相关系数的取值范围为-1到1,其中1表示完全正相关,-1表示完全负相关,0表示没有相关性。
我们常用的相关系数包括:
- Pearson相关系数:用于衡量两个连续变量之间的线性关系。取值范围在 -1 到 1 之间,其中 -1 表示完全负相关,1 表示完全正相关,0 表示无线性关系。
- Spearman等级相关系数:用于衡量两个变量之间的单调关系,不要求变量呈线性关系。对于等级或顺序数据更为适用。
在使用相关系数时,我们需要注意:样本越大,相关系数估计越稳定;有些相关系数对数据分布的假设比较敏感,确保你的数据满足相关方法的前提条件;相关性不代表因果关系,即使两个变量相关,也不能得出一个是因为另一个的结论。那么,对于这两种相关系数,我们如何选择呢?
Pearson相关系数
Pearson相关系数是一种用于度量两个连续变量之间线性关系强度和方向的统计量。它通常用字母 τ \tau τ 表示,取值范围在 -1 到 1 之间。
计算皮尔逊相关性时,要了解它要符合5个假设:连续变量;两个变量之间存在一定线性关系;两个变量应该大致符合正态分布;数据集中每个观测数据包括成对数据;数据集中不应包括极端异常值数据。
公式为: τ = ∑ ( x i − x ‾ ) ( y i − y ‾ ) ∑ ( x i − x ‾ ) 2 ⋅ ∑ ( y i − y ‾ ) 2 \tau=\frac {\sum(x_i-\overline x)(y_i-\overline y)}{\sqrt{\sum(x_i-\overline x)^2\cdot\sum(y_i-\overline y)^2}} τ=∑(xi−x)2⋅∑(yi−y)2∑(xi−x)(yi−y) 其中, x i x_i xi 和 y i y_i yi分别是两个变量的观察值, x ‾ \overline x x 和 y ‾ \overline y y分别是两个变量的均值。
Pearson相关系数假设两个变量之间的关系是线性的,因此它可能不适用于非线性关系的情况。在数据中存在异常值或数据不符合正态分布的情况下,Pearson相关系数的解释力也可能受到影响。在这些情况下,Spearman等级相关系数可能更为适用,因为它们对于非线性关系和异常值更具有鲁棒性。
Spearman等级相关系数
Spearman等级相关系数(Spearman’s rank correlation coefficient),通常用符号 ρ \rho ρ表示,是一种用于度量两个变量之间的单调关系(不一定是线性关系)的统计量。Spearman相关系数基于变量的等级或秩次而不是具体的数值。这使得它对于数据的分布形状和是否满足正态分布的要求都相对较为鲁棒。
计算Spearman等级相关系数的步骤:对于每个变量,将其观察值按照大小进行排名,即从最小到最大依次排列,并用秩次表示;对于每一对观察值,计算其等级差(即秩次差);计算等级差的平方和;使用公式将等级差的平方和转换为Spearman相关系数。
设 D i D_i Di为变量X和Y对应的秩次差,n为样本大小,Spearman相关系数的计算公式为: ρ = 1 − 6 ∑ D i 2 n ( n 2 − 1 ) \rho=1-\frac{6\sum D_i^2}{n(n^2-1)} ρ=1−n(n2−1)6∑Di2 Spearman相关系数的取值范围在 -1 到 1 之间:当 ρ=1 时,表示存在完全的正单调关系,即一个变量的增加伴随着另一个变量的增加;当 ρ=−1 时,表示存在完全的负单调关系,即一个变量的增加伴随着另一个变量的减少;当 ρ=0 时,表示两个变量之间没有单调关系。
Spearman相关系数对于非线性关系和异常值的敏感性相对较低,因此在数据不满足正态分布、存在异常值或者存在非线性关系的情况。
python代码实现
import pandas as pd# 示例数据
df = pd.DataFrame({'data1': [1, 2, 3, 4, 5], 'data2': [5, 4, 3, 2, 1]})# 计算 Pearson 相关系数
pearson_corr = df['data1'].corr(df['data2'])# 计算 Spearman 等级相关系数
spearman_corr = df['data1'].corr(df['data2'], method='spearman')print("Pearson 相关系数:", pearson_corr)
print("Spearman 等级相关系数:", spearman_corr)# Pearson 相关系数: -0.9999999999999999
# Spearman 等级相关系数: -0.9999999999999999
相关系数热力图:
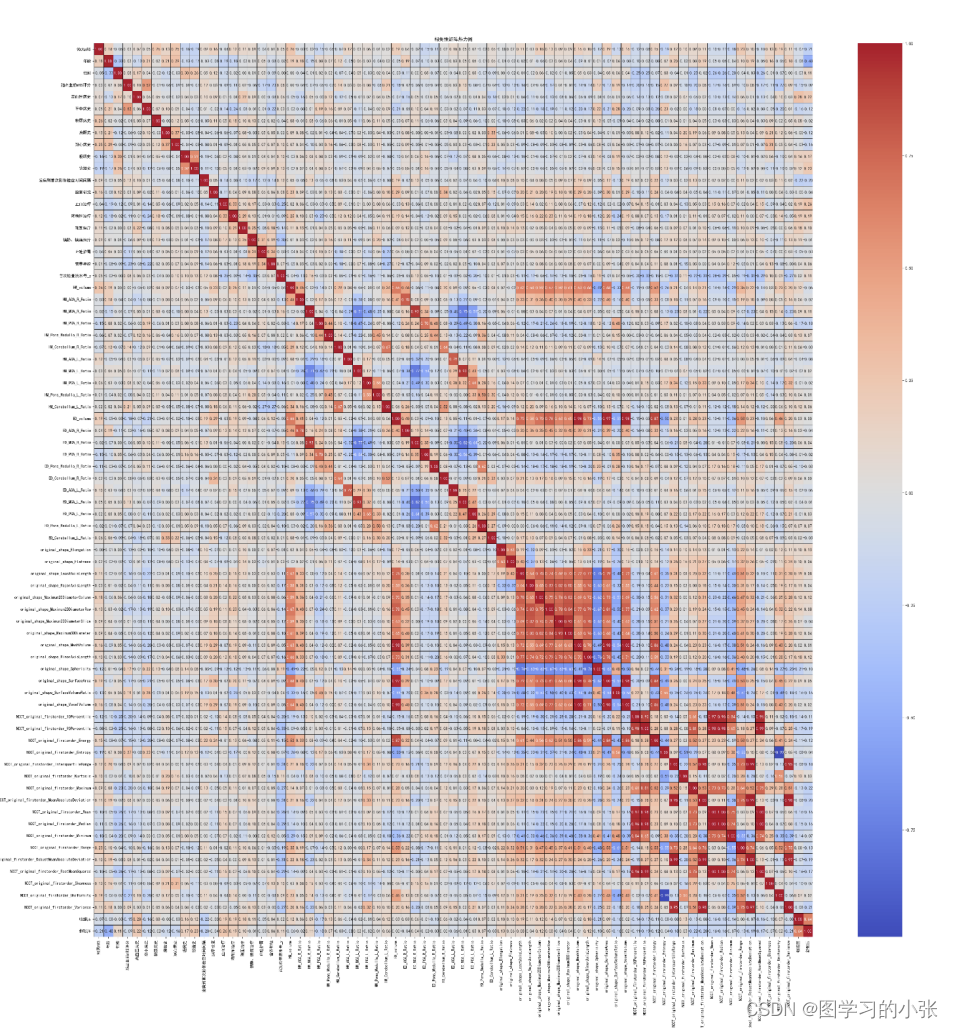
相关文章:

数学建模:数据相关性分析(Pearson和 Spearman相关系数)含python实现
相关性分析是一种用于衡量两个或多个变量之间关系密切程度的方法。相关性分析通常用于探索变量之间的关系,以及预测一个变量如何随着另一个变量的变化而变化。在数学建模中,这是常用的数据分析手段。 相关性分析的结果通常用相关系数来表示ÿ…...
使用pandas将excel转成json格式
1.Excel数据 2.我们想要的JSON格式 {"0": {"raw_data1": "Sam","raw_data2": "Wong","raw_data3": "Good","layer": "12v1"},"1": {"raw_data1": "Lucy…...
双向链表的插入、删除、按位置增删改查、栈和队列区别、什么是内存泄漏
2024年2月4日 1.请编程实现双向链表的头插,头删、尾插、尾删 头文件: #ifndef __HEAD_H__ #define __HEAD_H__ #include<stdio.h> #include<stdlib.h> #include<string.h> typedef int datatype; enum{FALSE-1,SUCCSE}; typedef str…...

Linux 驱动开发基础知识——总线设备驱动模型(七)
个人名片: 🦁作者简介:学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由…...
---03信号(软件中断)源码分析)
RTthread线程间通信(邮箱,消息队列,信号/软件中断)---03信号(软件中断)源码分析
信号 实际使用看这一个 #if defined(RT_USING_SIGNALS)rt_sigset_t sig_pending; /**< the pending signals 记录来了的信号 */rt_sigset_t sig_mask; /**< the mask bits of signal 记录屏蔽的信号 */rt_sigh…...
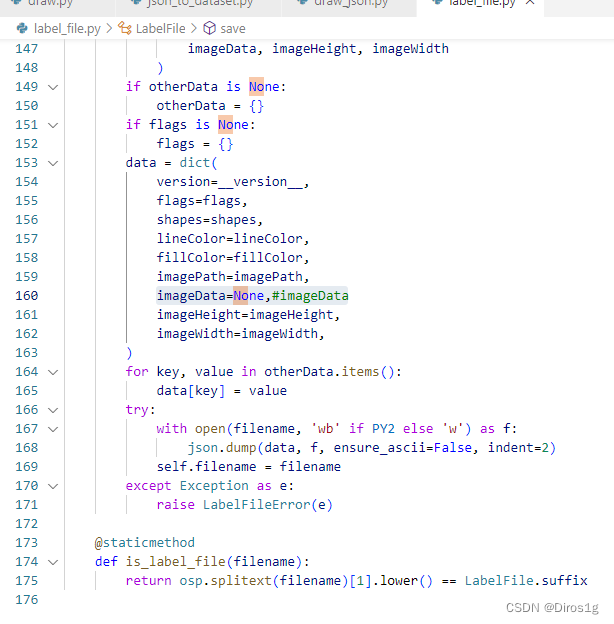
老版本labelme如何不保存imagedata
我的版本是3.16,默认英文且不带取消保存imagedata的选项。 最简单粗暴的方法就是在json文件保存时把传递过来的imagedata数据设定为None,方法如下: 找到labelme的源文件,例如:D:\conda\envs\deeplab\Lib\site-packages…...
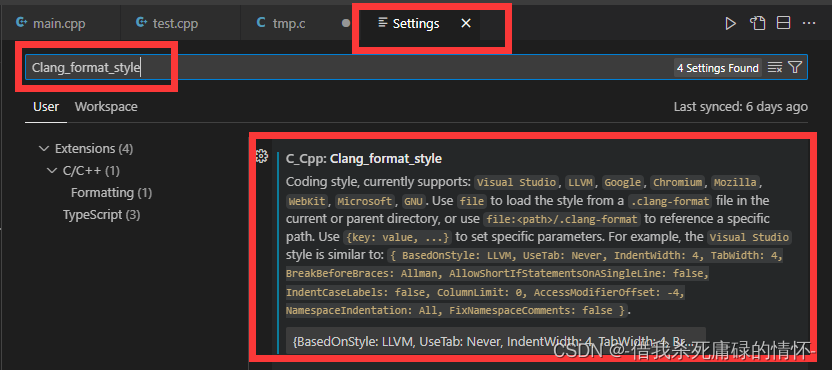
vscode 如何修改c/c++格式化风格,大括号不换行
在Visual Studio Code(VSCode)中,若要修改C代码格式化的风格以实现大括号不换行,通常会借助于插件C/C扩展中的ClangFormat配置。以下是具体的步骤: 确保已安装了C/C扩展: 打开VSCode的扩展市场(…...
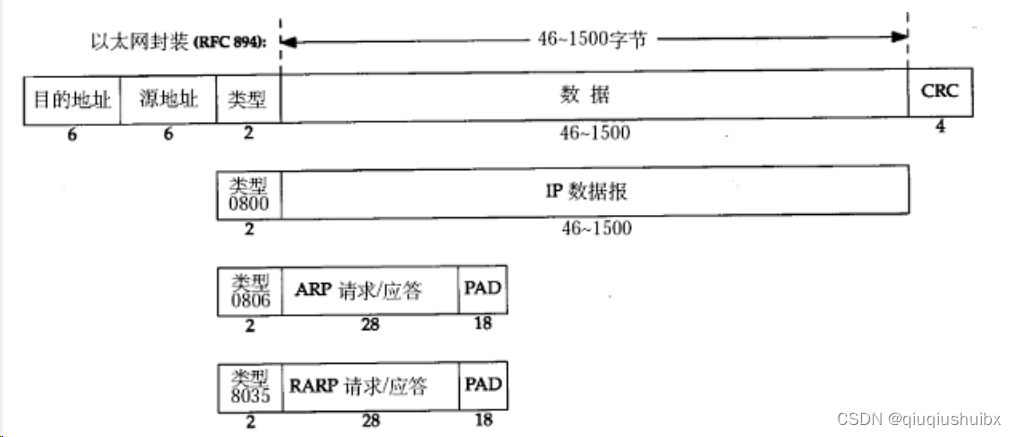
IP协议(2) 和 数据链路层协议基础
IP协议续 1.路由选择 在复杂的网络结构中,我们需要找到一个通往终点的路线,这就是路由选择 举个例子:我们在没有手机导航之前,想去一个地方得是到一个地方问一下路的方式最终找到目的地 路由的过程,其实就是样子问路的过程 1.当IP数据包到达路由器的时候,会查看目的IP 2.路由器…...

Flink-1.18.1环境搭建
下载 下载flink安装包 Index of /dist/flink/flink-1.18.1 下载flink-cdc安装包 Release Release 3.0.0 ververica/flink-cdc-connectors GitHub 安装 添加环境变量 vi ~/.bash_profile export FLINK_HOME=/home/postgres/flink/flink-1.18.1 export PATH=$PATH:$FL…...

deepin20.9安装及配置
安装deepin20.9很简单,刻录u盘 安装 一路next apt install nginx global vim-nox debian11 使用apt安装php, 使php多版本共存_debain11 php5-CSDN博客 vim LeaderF安装问题 - 知乎 debian10安装vue环境, 包括安装node.js-CSDN博客 debian安装vue3 nodejs20-CSD…...

2-2 动手学深度学习v2-损失函数-笔记
损失函数,用来衡量预测值和真实值之间的区别。是机器学习里面一个非常重要的概念。 三个常用的损失函数 L2 loss、L1 loss、Huber’s Robust loss 均方损失 L2 Loss l ( y , y ′ ) 1 2 ( y − y ′ ) 2 l(y,y^{\prime})\frac{1}{2}(y-y^{\prime})^{2} l(y,y′)21…...

非springboot 使用aop 切面
在非Spring Boot应用中使用AOP(Aspect Oriented Programming,面向切面编程)的代码实现需要依赖Spring AOP库。由于Spring AOP库并不直接支持非Spring应用,你需要将Spring AOP库作为依赖项添加到项目中,并使用Spring AO…...

MongoDB 字段中数据类型不一致序列化异常排查与处理
MongoDB 字段中数据类型不一致序列化异常排查与处理 背景如下,因为项目迁移愿意,一个使用Mongodb的业务拥有C#和Java两组Api。Java Api开发和测试都很顺利。上线一段时间后,客服反馈记录都不见了。查看数据库发现,时间字段拥有两…...

网络安全简介
网络安全: 网络安全攻击分为被动攻击和主动攻击。 1. 被动攻击:是指攻击者从网络上窃取了他人的通信内容,通常把这类的攻击称为截获,被动攻击只要有2种形式:消息内容泄漏攻击和流量分析攻击。由于攻击者没…...

【Docker】.NET Core 6.0 webapi 发布上传到Docker Desktop并启动运行访问,接口返回数据乱码解决方法
欢迎来到《小5讲堂》,大家好,我是全栈小5。 这是《Docker容器》系列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对…...
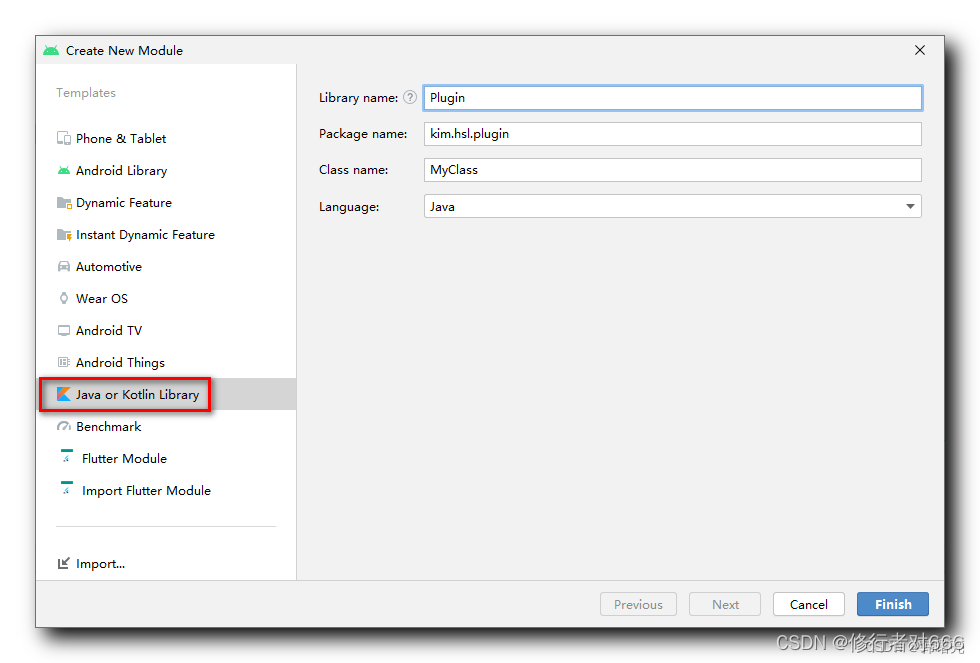
【Android Gradle 插件】自定义 Gradle 插件模块 ⑤ ( 完整总结 )
一、创建自定义插件类型模块 ( Java or Kotlin Library ) 选择 " 菜单栏 / New / New Module… " 选项 , 在 " Create New Module " 对话框中 , 选择 创建 " Java or Kotlin Library " 类型的依赖库 ; 二、手动导入相关依赖 ( Java | Groovy | …...
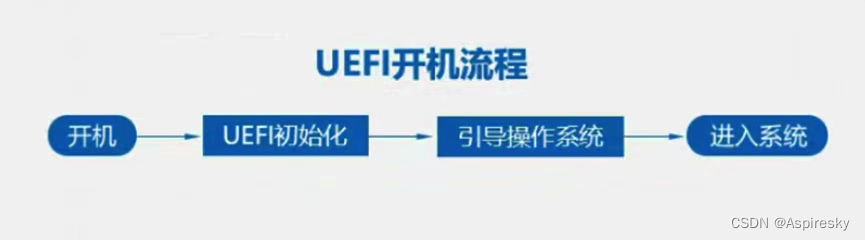
浅析现代计算机启动流程
文章目录 前言启动流程概述磁盘分区格式MBR磁盘GPT磁盘隐藏分区 传统BIOS引导传统BIOS启动流程 UEFI引导UEFI引导程序UEFI启动流程 引导加载程序启动操作系统相关参考 前言 现代计算机的启动是一个漫长的流程,这个流程中会涉及到各种硬件的配置与交互,包…...
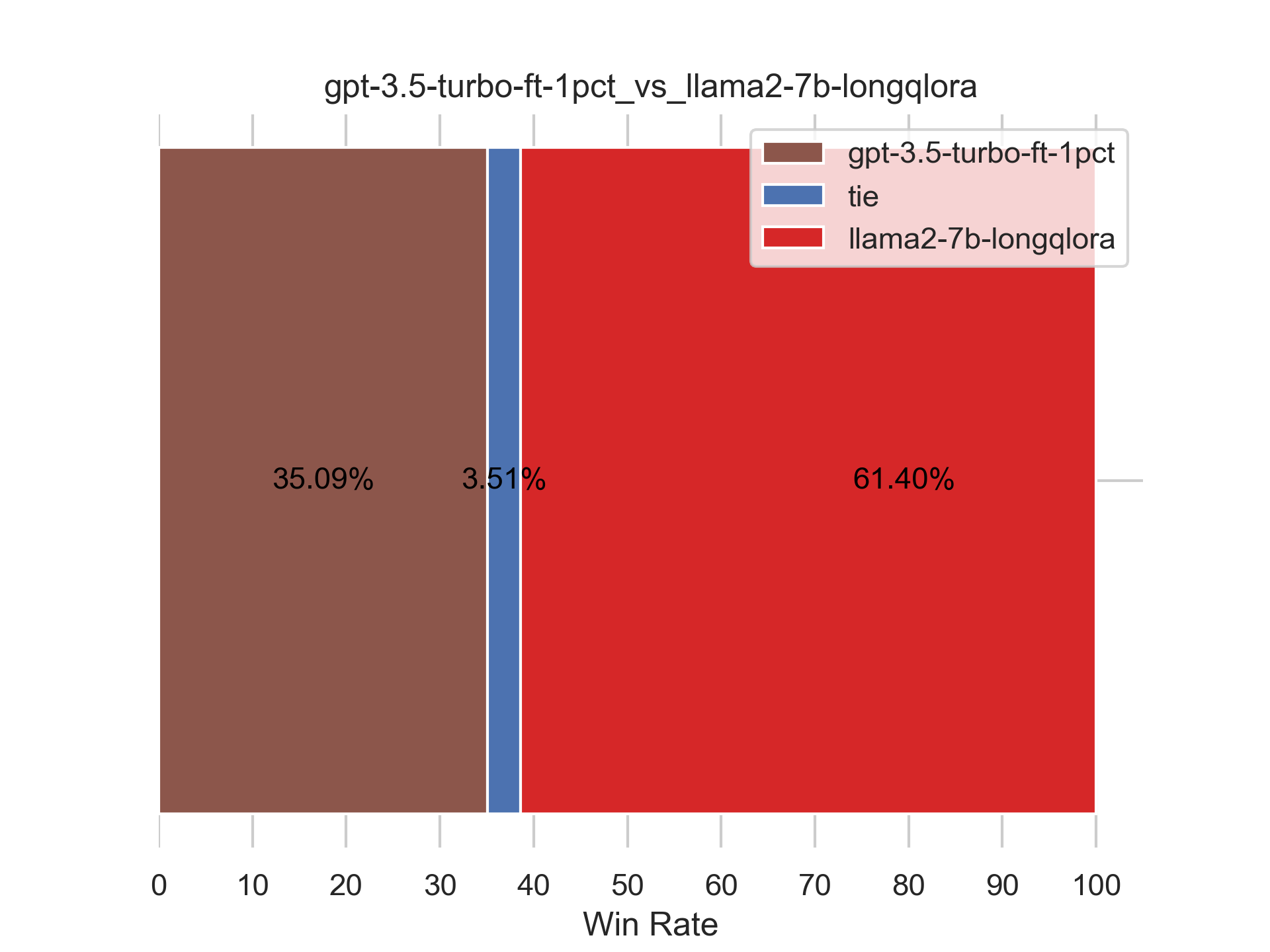
七月论文审稿GPT第2.5和第3版:分别微调GPT3.5、Llama2 13B以扩大对GPT4的优势
前言 自去年7月份我带队成立大模型项目团队以来,我司至今已有5个项目组,其中 第一个项目组的AIGC模特生成系统已经上线在七月官网第二项目组的论文审稿GPT则将在今年3 4月份对外上线发布第三项目组的RAG知识库问答第1版则在春节之前已就绪至于第四、第…...
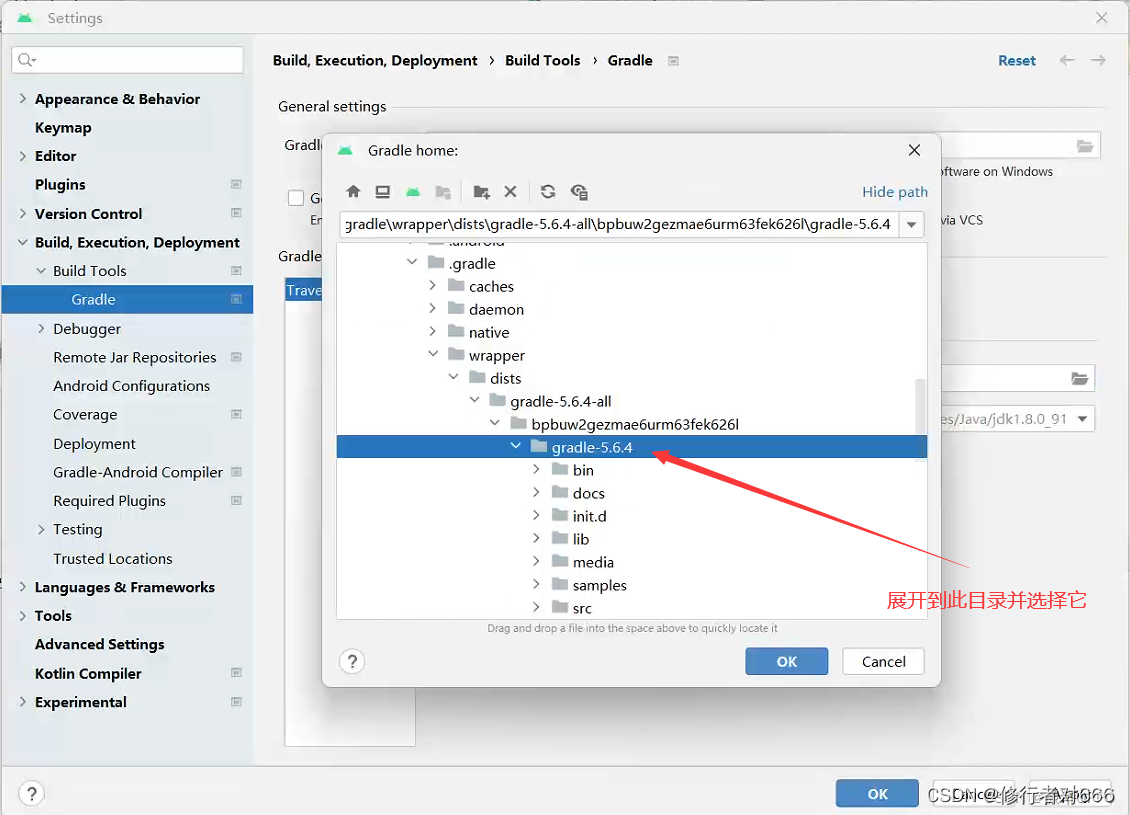
Android Studio导入项目 下载gradle很慢或连接超时
AS最常见的问题之一就是下载gradle非常慢,还经常出现下载失败的情况,没有gradle就无法build项目,所以一定要先解决gradle的下载问题,下面教大家两种常用方法 手动下载压缩包并替换 1、关闭Android Studio,复制下面的网…...
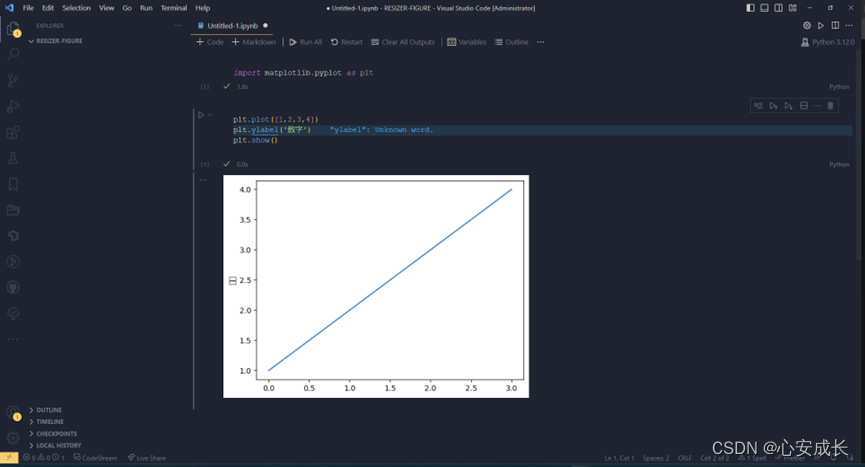
如何使用VSCode上运行Jupyter,详细案例过程出可视化图
Python作为最受AI喜欢的语言之一,我们与大家共同学习下如何在VS Code上运行Jupyter,并且用简单案例实现出图。 环境 VS Code version: 1.80.1 Python: 3.12.0 小白安装过程: 在准备好基础环境,小白心想,AI可是霸占科…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
