基础数学问题整理
最近刷了一些关于基础数学问题的题目,大致是关于组合数、分解质因数还有一些思维题,题目来自洛谷的【数学1】基础数学问题 - 题单 - 洛谷,很多思路还是之前没有见过的,都是简单到一般难度的题目(橙、题、绿题),特别做个整理。
目录
组合数问题
编号
组合数问题
分解质因数
Hankson 的趣味题
细胞分裂
思维题
找筷子
进制转换
又是毕业季II
组合数问题
编号
编号 - 洛谷
这一题的意思就是有若干个位置,每个位置的数字范围都是 1~M[i],每个位置放置的数字都不相同,有多少排列数。
首先升序排序,因为选择更少的一定是先排,前面范围小的可以选择的,后面范围大的也一定可以选择,而且前面排列的也一定是后面拍的其中一个选择,那么对于位置x,此时的选择就有M[i]-x+1,总的排列数量就是(M[1]-1+1)*(M[2]-2+1)*...*(M[n]-n+1),显然若其中任意一个数为0,也就是到这个位置,没有选择了,那么就是无法满足。
记得随时取模。
#include<stdio.h>
#include<algorithm>
using namespace std;
#define ll long long
#define MOD 1000000007int cmp(int x, int y) {return x < y;
}int a[100];
int main()
{int n; scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", a+i);}sort(a + 1, a + n + 1, cmp); // 升序排序首先需要计算出所有的组合数ll ans = 1;for (int i = 1; i <= n; i++) {if (a[i] < i) {printf("0\n");return 0;}ans = ans * (a[i]-i+1) % MOD;}printf("%lld\n", ans);return 0;
}组合数问题
[NOIP2016 提高组] 组合数问题 - 洛谷
这一题略复杂,需要计算对于所有0<i≤n,0<j≤min(i,m),有多少对(i,j)满足k|C(i,j),其中X|Y定义为Y mod X = 0。
对于排列数C(n,m),存在C(n,m)=C(n-1,m-1)+C(n-1,m),也就是在n个东西里面选m个东西,等于除掉任意一个东西x,选x并且在剩下n-1个选m-1的情况,加上在n-1个里面选m个东西,(学过排列组合应该能get?),也可以从代数角度证明等式。这个在图形中就表现为杨辉三角,这也是这一题计算任意C(i,j)的关键所在。
预处理出杨辉三角后存在数组中,此时问题就变成了在一个杨辉三角中画一个矩形,计算矩形中有多少个满足的点,就比如下面计算样例1的i=3,j=3有多少满足2的倍数。
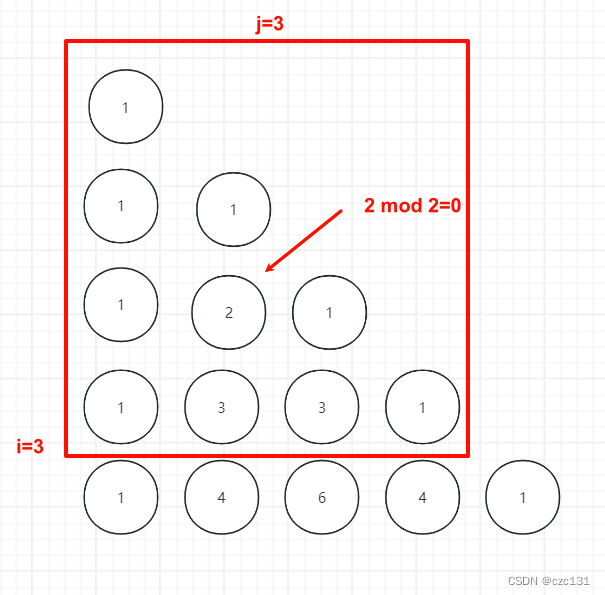
因为有多个询问,那么问题就转为了对于任意i和j,怎么快速计算矩形内满足的数量,读题可以发现, k是恒定的,所以可以预处理出所有(i,j)对应的结果。
定义sum[i][j]为i行到j的前缀和,f[i][j]为到i行到j列(不包括大于j列的)满足mod k=0的,也就是答案数组,那么f[i][j]=f[i-1][j]+sum[i][j]。
#include<stdio.h>
#include<algorithm>
using namespace std;
int tran[2024][2024];//记录杨辉三角
int f[2024][2024];//状态转移 //f[n][m]=f[n-1][m-1]+f[n-1][m]
int t,m,n,k;
int main()
{scanf("%d%d", &t,&k);int maxi = 2010;for (int i = 0; i < maxi; i++)tran[i][0] = 1;int j;for (int i = 1; i <= maxi; i++) {int sum_tmp = 0;//当前行的和for (j = 1; j <= i; j++) {//printf("(%d,%d)%d+%d,", i,j,tran[i - 1][j - 1], tran[i - 1][j]);tran[i][j] = (tran[i - 1][j - 1] + tran[i - 1][j])%k;// 因为后面反正也是要看是不是k的倍数的//printf("%d,", tran[i][j]);if (tran[i][j] == 0) {sum_tmp++;}f[i][j] = f[i - 1][j] + sum_tmp; // 计算数量//printf("(i=%d,j=%d)%d ",i,j, f[i][j]);}f[i][j] = f[i][j - 1];//这是为了下面一行的转移//printf("\n");}for (int epoch = 1; epoch <= t; epoch++) {scanf("%d%d", &n, &m);m = min(m, n);//printf("n=%d m=%d\n", n, m);printf("%d\n", f[n][m]);}return 0;
}分解质因数
Hankson 的趣味题
[NOIP2009 提高组] Hankson 的趣味题 - 洛谷
这一题要一个数x满足和a0的公约数是a1,和b0的最小公倍数是b1,求满足的x数量。
《趣味题》确实是很有趣味,不过前提是能做出来,一开始看到这种题目也是傻眼,完全无从下手。容易得出的是x=k1*a1=b1/k2(a1是公约数,b1是公倍数),因此k1*k2=b0/a0。
此时还需要知道的就是在什么时候k1和k2是合法的,可以证明若x=k1*a1,a0=k2*a1,此时gcd(k1,k2)=1,因为如果k1和k2还有公约数t,那么此时x和a0的最大公约数就应该是t*a1而不是a1,同理对于b的也是类似,因此可以得到判断条件,也就是系数之间的最大公约数都是1。枚举k1并计算出k2判断是否合法,统计出数量。
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
int gcd(int x, int y) {return y == 0 ? x : gcd(y, x%y); // 一句话搞定 这个相当于要是x>y那么就换个位置
}bool check(int x, int y) {if (gcd(x, y) == 1)return 1;return 0;
}int main()
{int t, a0, a1, b0, b1;scanf("%d", &t);int cnt;while (t--) {scanf("%d%d%d%d", &a0, &a1, &b0, &b1);// 开始枚举cnt = 0;int mul_k = b1 / a1;//printf("mul_k=%d\n", mul_k);//printf("%d\n", int(sqrt(mul_k)));int x;// a1是公约数,b1是公倍数for (int now = 1; now<= sqrt(mul_k); now++) { // x=k1*a1=b1/k2 这里枚举的是k1(防止迭代变量变化,这里使用now作为迭代变量)int k = now;if (mul_k%k)continue;// 判断k时的情况x = k * a1; // 算出xif (x%a1 == 0 && b1 % x == 0) { // 满足倍数和约数if (check(a0 / a1, k) && check(b1 / b0, mul_k / k)) {cnt++;}}if (k*k == mul_k) continue;//重复的不用再算一次// 判断mul_k/k时的情况k = mul_k / k;x = k * a1; // 算出xif (x%a1==0 || b1 % x==0) { // 满足倍数和约数if (check(a0 / a1, k) && check(b1 / b0, mul_k / k)) {cnt++;}}}printf("%d\n", cnt);}return 0;
}细胞分裂
[NOIP2009 普及组] 细胞分裂 - 洛谷
这一题需要计算的是一个数(细胞数)及其幂次是否可以为一个数(试管数)的倍数,涉及三个知识点。
- 一个大于2的数都可以分解为若干质数的乘积。
- 一个数是另一个数的倍数满足这个数的质数分解列表包含另一个数的质数分解列表。
- 幂次不改变质数列表的元素,只改变次数,假设m的分解包含t个x,那么m^n包含t*n哥x。
那么这题的思路就很简单了,就是先分解试管数量,再逐个分解细胞数,一个个计算结果找出最小的。
#include<stdio.h>
#include<math.h>
#include<algorithm>
#define N 30000
using namespace std;
struct PipeNode {int num;int idx; // 当前质因数idx有num个
}pipeNode[N+20];
struct Flags {int num; int x0; // 标记当前所属的初值(也就是每种细菌),每次分解质因数都要标记是属于哪种的,如果不匹配就是前面的,那么桶就不需要重复初始化
}flag[N+20]; // 下标就是质因数的数值
int n,m1,m2; // 细菌总数
int a[N+20];
int primes[N+1],prime_cnt;
int pipeCnt;// 试管质因数数量
bool check_prime(int x) {if (x % 2 == 0)return 0;for (int i = 3; i <= sqrt(x); i++) {if (x%i == 0)return 0;}return 1;
}int main()
{scanf("%d", &n);scanf("%d%d", &m1, &m2);for (int i = 1; i <= n; i++)scanf("%d", a + i);// 质因数打表primes[++prime_cnt] = 2;for (int i = 3; i <= N + 10; i++) {if (check_prime(i))primes[++prime_cnt] = i;}// 首先给试管做质因数分解if (m1 == 1) {printf("0\n");//一个就是初始数量,肯定可以满足return 0;}else {for (int i = 1; i <= prime_cnt; i++) {// 枚举质因数if (m1%primes[i] == 0) { // 如果可以分解pipeNode[++pipeCnt].idx = primes[i];pipeNode[pipeCnt].num = 0;while (m1%primes[i] == 0) {pipeNode[pipeCnt].num++;m1 /= primes[i];}}if (m1 == 1)break;//分解结束}}for (int i = 1; i <= pipeCnt; i++)pipeNode[i].num *= m2;// 质因数*倍数// 开始检查每种细菌int ans = 0x3f3f3f3f;//存储需要再过的最短时间for (int index = 1; index <= n; index++) {int x0 = a[index];//printf("a[index]=%d\n", a[index]);// 分解x0并装进桶里int x0_copy = x0;for (int i = 1; i <= prime_cnt; i++) {if (x0_copy%primes[i] == 0) {flag[primes[i]].x0 = x0;flag[primes[i]].num = 0;while (x0_copy%primes[i] == 0) {flag[primes[i]].num++;x0_copy /= primes[i];}}if (x0_copy == 1)break;}// 检查当前细菌是否可以达到菌均分int res = -1; // 找最大值,存在不符合要求的就是-1for (int i = 1; i <= pipeCnt; i++){ // 检查所有菌int num = pipeNode[i].num;int idx = pipeNode[i].idx;if (flag[idx].x0 != x0) {//x0当前没有质因数分解到idx(试管的某个质因数)res = -1;break;}int flag_num = flag[idx].num; // 菌初始值// 计算需要多长时间int det = max(0,num - flag_num);if (det) {res = max(res,(det - 1) / flag_num + 1);}else {res = max(res,0);}if (res > ans)break;//没必要算了}if (res != -1) {ans = min(ans, res);}if (ans == 0)break;//不用算了}if (ans == 0x3f3f3f3f) {printf("-1\n");}else {printf("%d\n", ans+1); // 初始时间为1}return 0;
}思维题
找筷子
找筷子 - 洛谷
这一题需要找到若干个数中,唯一的数量为奇数的那个数字,思路感觉比较巧妙,利用了异或的思路,因为一个数异或偶数次后为0,因此把全部数字取异或后就可以得到个数为奇数的那个数字。
一个数异或两次就是0可以查一下异或的定义,两次为0,那么异或偶数次都是0。
#include<stdio.h>
int main()
{int a=0,n,x;scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", &x);a ^= x;// 取异或}printf("%d\n", a);return 0;
}
进制转换
[NOIP2000 提高组] 进制转换 - 洛谷
这一题涉及到了负进制的概念,比较新颖,一开始确实是没想到十进制数字转为负数进制的方法,后来查了一下,转为负进制也是使用短除法。
类似转为二进制一直除以2,最后从余数逆向连起来得到结果,对于负二进制,也是除以-2,但是直接用C语言的'%'符号计算是会得到负余数的,比如除数为3,转为-2进制,(-3)÷(-2)=1...-1(1余-1),此时为了让余数为非负,把余数的一个被除数放到商,也就是(-3)÷(-2)=2...1,此时2*(-2)+1=-3,然后继续2÷(-2)=-1...0...一直到最后商为1或者为0,那么可以结束(这里一时忘记当时怎么想的了,0结束好理解,1结束应该是因为再除也是一样的结果?)。
去掉前导0不要忘记。
#include<stdio.h>
int a,b;
int res[100000], cnt;
int main()
{scanf("%d%d", &a, &b);int a_copy = a;while (a != 1 && a != 0) {int div = a / b;int mod = a % b;//printf("div=%d mod=%d\n", div, mod);if (mod < 0) {mod -= b;div++;}res[++cnt] = mod;a = div;}if(a) res[++cnt] = a; // 最后一位是1保存下来,0就不要了printf("%d=", a_copy);for (int i = cnt; i >=1; i--) {if(res[i]<=9)printf("%d", res[i]);else printf("%c", 'A' + res[i] - 10);}printf("(base%d)", b);return 0;
}又是毕业季II
又是毕业季II - 洛谷
这一题要计算从n个数中任意取m(1≤m≤n)个数,分别对应的最大公约数。
这一题的思路有点巧妙,当然不是我想到的...
m越大,最大公约数越小,也就是选的越多,那么最大公约数一定越小(如果m个对应了更大的最大公约数,那么m-1个也能满足取得这个最大公约数,那么就矛盾了)。首先计算出每个数的所有因子(不是质因子),并给这些因子计数,然后从后往前看(后也就是公因数可能的最大值,也就是max(a[1~n]),也就是m=1对应的最大公约数),要是某个数字作为因子的个数恰好为m个,那么就是任选m个数字对应的最大公因数(这m个数就是对应此时最大公约数的选择方案,可以细品一下)
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
#define N 1000000
int n;
int flag[N + 10];
int main()
{scanf("%d", &n);int x;int maxx = -1;for (int i = 1; i <= n; i++) {scanf("%d", &x);maxx = max(x, maxx);// 分解所有质因数,存入flagfor (int j = 1; j < sqrt(x); j++) {if (x%j == 0) {flag[j]++;flag[x / j]++;}}int sqrt_x = sqrt(x); // 特判if (pow(sqrt_x,2) == x) {flag[sqrt_x]++;}}for (int i = 1; i <= n; i++) {while (flag[maxx] < i)maxx--;printf("%d\n", maxx); // 打印当前位置}return 0;
}这个题单其实还有一些没写,确实有点超出理解水平了,先记录到这里。
相关文章:

基础数学问题整理
最近刷了一些关于基础数学问题的题目,大致是关于组合数、分解质因数还有一些思维题,题目来自洛谷的【数学1】基础数学问题 - 题单 - 洛谷,很多思路还是之前没有见过的,都是简单到一般难度的题目(橙、题、绿题ÿ…...
【Linux】环境基础开发工具的使用(一)
前言:在此之前我们学习了一些Linux的权限,今天我们进一步学习Linux下开发工具的使用。 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:Linux的深度刨析 👈 💯代码仓库:卫卫周大胖的学习日记…...
))
突破编程_C++_面试(基础知识(5))
面试题9:什么是内存地址 内存地址是指计算机内存中存储变量或对象的地址。内存空间大小就是寻址能力,即能访问到多少个地址,比如 32 位机器内存空间大小就是 2^32 4294967296,也就是 4 GB 。每个变量或对象在内存中都有一个唯一…...

十分钟掌握Go语言==运算符与reflect.DeepEqual函数处理interface{}值的比较规则
在 Go 语言中,interface{} 类型是一种特殊的接口类型,它表示任意类型的值。你可以使用 运算符来检测任意两个 interface{} 类型值的相等性,比较的规则和一般的接口类型一样,需要满足以下条件: 两个 interface{} 值的…...

Unity3d Shader篇(一)— 顶点漫反射着色器解析
文章目录 前言一、顶点漫反射着色器是什么?1. 顶点漫反射着色器的工作原理 二、编写顶点漫反射着色器1. 定义属性2. 创建 SubShader3. 编写着色器程序段4. 完成顶点着色器5. 完成片段着色器 三、效果四、总结 前言 在 Unity 中,Shader 可以用来实现各种…...

WordPress主题YIA的文章页评论内容为什么没有显示出来?
有些WordPress站长使用YIA主题后,在YIA主题设置的“基本”中没有开启“一键关闭评论功能”,而且文章也是允许评论的,但是评论框却不显示,最关键的是文章原本就有的评论内容也不显示,这是为什么呢? 根据YIA主…...
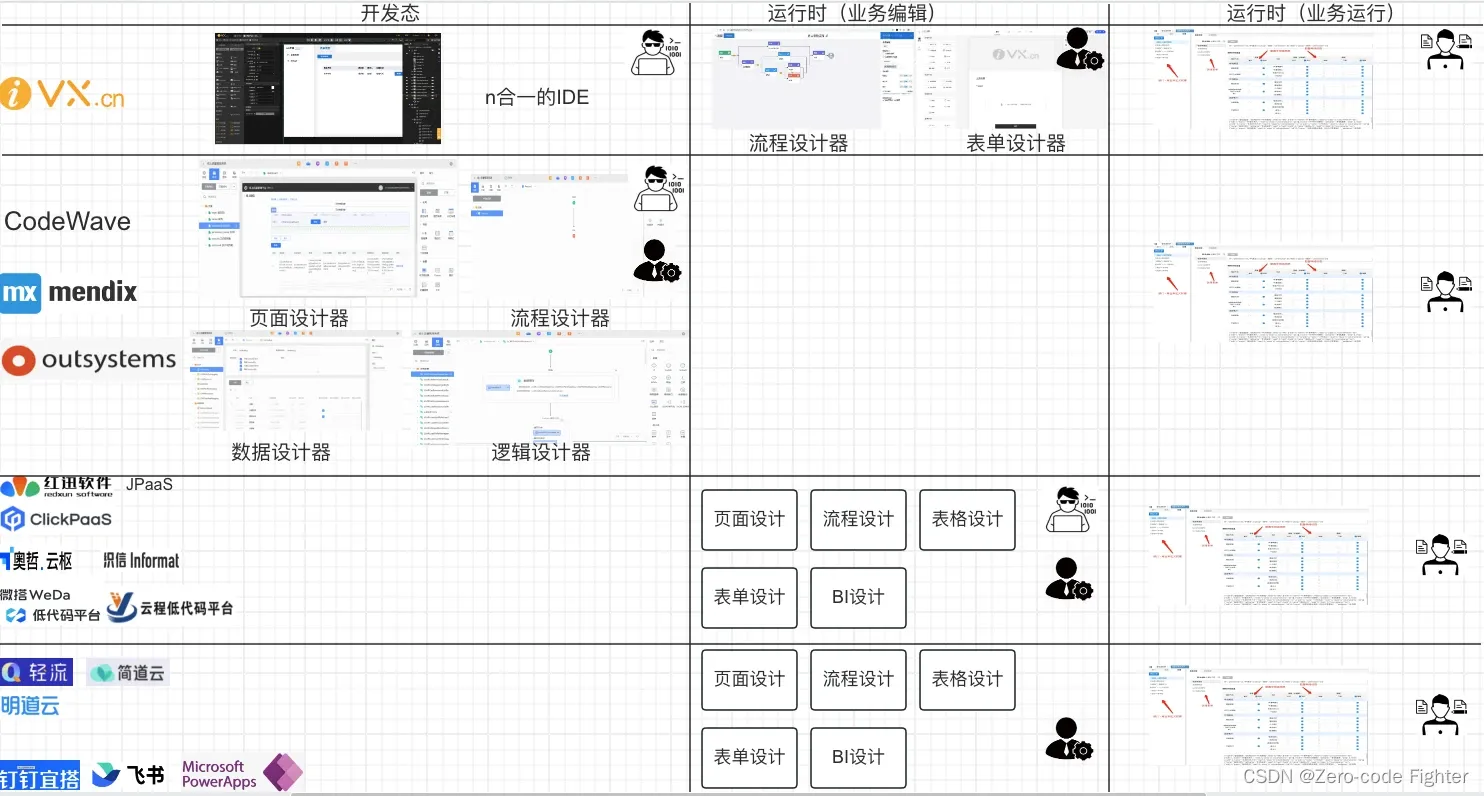
选择低代码应该注意什么?如何选择?
我查看了几乎所有的介绍低代码的总结和分析报告,几乎都没有把低代码最底层的产品逻辑说清楚。今天我尝试不用复杂的技术名词,也不用代码,把这个事儿给大家说明白,低代码到底怎么回事儿!(人云亦云那些&#…...
橘子学linux调优之工具包的安装
今天在公司无聊的弄服务器,想着有些常用的工具包安装一下,这里就简单记录一下。 一、sysstat的安装和使用 1、安装 我是通过源码的方式安装的,这样的好处在于可以自由选择你的版本,很直观。 直接去github上找到sysstat的地址&a…...

函数的连续与间断【高数笔记】
【连续】 分类,分几个?每类特点? 连续条件,是同时满足还是只需其一? 【间断】 分类,分几个大类,又分几个小类?每类特点? 间断条件,是同时满足还是只需其一&am…...

游戏如何选择服务器
选择游戏服务器是一个综合性的过程,涉及到的因素包括但不限于游戏类型和规模、硬件配置、网络质量、安全性、服务商的声誉以及地理分布等。以下是一些具体的指导原则: 游戏类型和规模:根据游戏的具体需求来选择合适的服务器。例如࿰…...

ubuntu20安装mysql8
1.安装 sudo apt update sudo apt install mysql-server-8.0 -y2.查看运行状态 yantaoubuntu20:~$ sudo systemctl status mysql ● mysql.service - MySQL Community ServerLoaded: loaded (/lib/systemd/system/mysql.service; enabled; vendor preset:>Active: active …...
07 SB3之@HttpExchange(TBD)
HttpExchange是SpringBoot3的新特性. Spring Boot3 提供了新的 HTTP 的访问能力,封装了Http底层细节. 通过接口简化 HTTP远程访问,类似 Feign 功能。 SpringBoot 中定义接口提供 HTTP 服务 --> 框架生成的代理对象实现此接口 --> 框架生成的代理…...

Redis数据淘汰策略
Redis作为一种高性能的键值存储数据库,通常用于缓存和提高数据检索速度。然而,由于内存资源有限,当内存不足以容纳所有数据时,Redis就需要采取一些策略来删除部分数据,以确保新的数据能够被写入。这就引入了数据淘汰策…...

Git的一些基本操作
初始git 我们给出下面的一个场景,在大学里,一些老师在我们做完实验之后喜欢让我们交实验报告,假设我们有一个比较追求完美的老师和一个勤奋的学生,这个学生叫做小帅,那天小帅桑勤奋的完成实验报告,在第二天…...

Spring Boot中异步线程池@Async
很多业务场景需要使用异步去完成,比如:发送短信通知。要完成异步操作一般有两种: 1、消息队列MQ 2、线程池处理。 我们来看看Spring框架中如何去使用线程池来完成异步操作,以及分析背后的原理。 一. Spring异步线程池的接口类 …...
ArcGIS学习(五)坐标系-2
3.不同基准面坐标系之间的转换 在上一关中,我们学习了ArcGIS中的投影(投影栅格)工具,并以"WGS1984地理坐标系与WGS1984的UTM投影坐标系的转换”为例进行讲解。 "WGS1984地理坐标系与WGS1984的UTM投影坐标系的转换”代表的是同一个基准面下的两个坐标的转换。 …...
2024Node.js零基础教程(小白友好型),nodejs新手到高手,(五)NodeJS入门——http模块
044_http模块_创建HTTP服务端 hello,大家好,那这个小节我们来使用 nodejs 创建一个 http 的服务,有了这个 http 服务之后,我们就可以处理浏览器所发送过来的请求,并且还可以给这个浏览器返回响应。 顺便说一下&#x…...

sklearn.preprocessing 标准化、归一化、正则化
文章目录 数据标准化的原因作用归一化最大最小归一化针对规模化有异常的数据标准化线性比例标准化法log函数标准化法正则化Normalization标准化的意义数据标准化的原因 某些算法要求样本具有零均值和单位方差;需要消除样本不同属性具有不同量级时的影响: ① 数量级的差异将导…...
 文件与目录操作)
Windows系统编程(一) 文件与目录操作
以下程序需要包含<Windows.h>头文件 创建打开文件 HANDLE hFile CreateFile("D:\\rkvir.ini", GENERIC_READ | GENERIC_WRITE, NULL, NULL, OPEN_ALWAYS, FILE_ATTRIBUTE_NORMAL, NULL); 此处打开文件,参数依次 已有文件的路径,注意…...

6-2、T型加减速计算简化【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:本节介绍简化T型加减速计算过程,使其适用于单片机数据处理。简化内容包括浮点数转整型数计算、加减速对称处理、预处理计算 一、浮点数转整型数计算 根据上一节内容已知 常用的晶振大小…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
