堆排及时间复杂度分析
箴言:
初始阶段,不需要去纠结那一种更优美,非要找出那一种是最好的,其实能解决问题的就是好办法。
一,常见排序时间复杂度
| 冒泡 | 快排 | 归并 | 堆排 | 桶排 | |
|---|---|---|---|---|---|
| 时间 | O(n^2) | O(nlogn) | O(nlogn) | O(nlogn) | kn |
| 空间 | O(1) | O(1) | O(nlogn) | O(1) | kn |
二,堆排
前情提要:
堆属于完全树,完全树可以理解为一个数组。如果不是完全树,就没办法和数组等价,就不会有下面这种父级和子级之间的关系。
已知父级下标i
左孩子下标: 2*i+1
右孩子下标: 2*i+2
已知孩子结点j(无论左还是右)
父级下标 (j-1)/2堆排序过程:
堆排序分成两个阶段,第一个阶段从由无序数组建立一个大/小根堆,第二个阶段在大/小根堆的基础上调整,形成有序数组。
从无序数组到大根堆:
对于数组中每一个元素,我们需要将其和其父级做对比,若比父级大,则进行交换,直到最顶层为止。
代码:(其实找父亲的时候可以不区分左右减一除二即可,我这里就不改了)
public static void builddui(int[] arr) {for (int i = 0; i < arr.length; i++) {int j = i;int p = 0;if (j % 2 == 1) {//左孩子p = (j - 1) / 2;} else {p = (j - 2) / 2;//右孩子}while (p >= 0 && arr[p] < arr[j]) {int t = arr[p];//交换位置arr[p] = arr[j];arr[j] = t;j = p;p = (j - 1) / 2;}}}从大根堆到有序序列:
最后一个位置和堆顶交换,将交换之后的堆顶下沉到正确的位置。然后堆顶和倒数第二个交换,堆顶下沉到正确的位置,直到剩下一个为止。这是一个堆顶元素不断下沉的过程。
代码:(r表示的是最后一个的索引位置)
public static void weichidui(int[] arr, int r) {int t = arr[r];arr[r] = arr[0];arr[0] = t;int cur = 0;//当前下标while (2 * cur + 1 < r) {int index = 2 * cur + 1;int maxv = arr[index];if (2 * cur + 2 < r && arr[index] < arr[2 * cur + 2]) {index = 2 * cur + 2;maxv = arr[2 * cur + 2];}if (maxv > arr[cur]) {int tmp = arr[cur];arr[cur] = arr[index];arr[index] = tmp;}cur = index;}}时间复杂度分析:
上述两个阶段分别分析: 从无序序列到建成大顶堆: 已知数组中数量为n,每正确插入一个元素,时间复杂度为logn(因为树的深度为logn),因为插入n个元素,时间复杂度为nlogn。
从大顶堆到有序序列:每次首尾交换之后都需要将堆顶元素下沉到正确的位置,时间复杂度为logn(因为树的深度为logn,比较交换次数其实是小于logn的,但是理解为logn就行),需要下沉n次,所以时间复杂度是nlogn。
ABOVE ALL,堆排时间复杂度为2nlogn,也就是O(nlogn),一切操作都是在原数组上进行的操作,所以空间复杂度为O(1)。
堆排序是一个完美的排序方式,无论时间或者空间,数据量小的时候差距不明显,数据量越大,优势就会越明显。
代码:
数组:[34,56,23,33,5,46,4,57,6,76,34,42,634,6,536,3,3423,3,1,5,537,3,57,3563,4,65,764,4]
import java.util.Arrays;/*** @Author YuLing* @Date 2024-02-07 19:14* @Description:* @Version 1.0*/
public class dui {public static void main(String[] args) {int[] arr = new int[]{34,56,23,33,5,46,4,57,6,76,34,42,634,6,536,3,3423,3,1,5,537,3,57,3563,4,65,764,4};builddui(arr);System.out.println(Arrays.toString(arr));for (int i = 0; i < arr.length; i++) {weichidui(arr, arr.length - 1 - i);}System.out.println(Arrays.toString(arr));}public static void builddui(int[] arr) {for (int i = 0; i < arr.length; i++) {int j = i;int p = 0;if (j % 2 == 1) {//左孩子p = (j - 1) / 2;} else {p = (j - 2) / 2;//右孩子}while (p >= 0 && arr[p] < arr[j]) {int t = arr[p];//交换位置arr[p] = arr[j];arr[j] = t;j = p;p = (j - 1) / 2;}}}public static void weichidui(int[] arr, int r) {int t = arr[r];arr[r] = arr[0];arr[0] = t;int cur = 0;//当前下标while (2 * cur + 1 < r) {int index = 2 * cur + 1;int maxv = arr[index];if (2 * cur + 2 < r && arr[index] < arr[2 * cur + 2]) {index = 2 * cur + 2;maxv = arr[2 * cur + 2];}if (maxv > arr[cur]) {int tmp = arr[cur];arr[cur] = arr[index];arr[index] = tmp;}cur = index;}}
}
输出:
[3563, 634, 3423, 57, 537, 764, 76, 34, 6, 56, 57, 46, 536, 4, 6, 3, 33, 3, 1, 5, 5, 3, 34, 23, 4, 42, 65, 4]
[1, 3, 3, 3, 4, 4, 4, 5, 5, 6, 6, 23, 33, 34, 34, 42, 46, 56, 57, 57, 65, 76, 536, 537, 634, 764, 3423, 3563]
相关文章:

堆排及时间复杂度分析
箴言: 初始阶段,不需要去纠结那一种更优美,非要找出那一种是最好的,其实能解决问题的就是好办法。 一,常见排序时间复杂度 冒泡快排归并堆排桶排时间O(n^2)O(nlogn)O(nlogn)O(nlogn)kn空间O(1)O(1)O(nlogn)O(1)kn 二ÿ…...
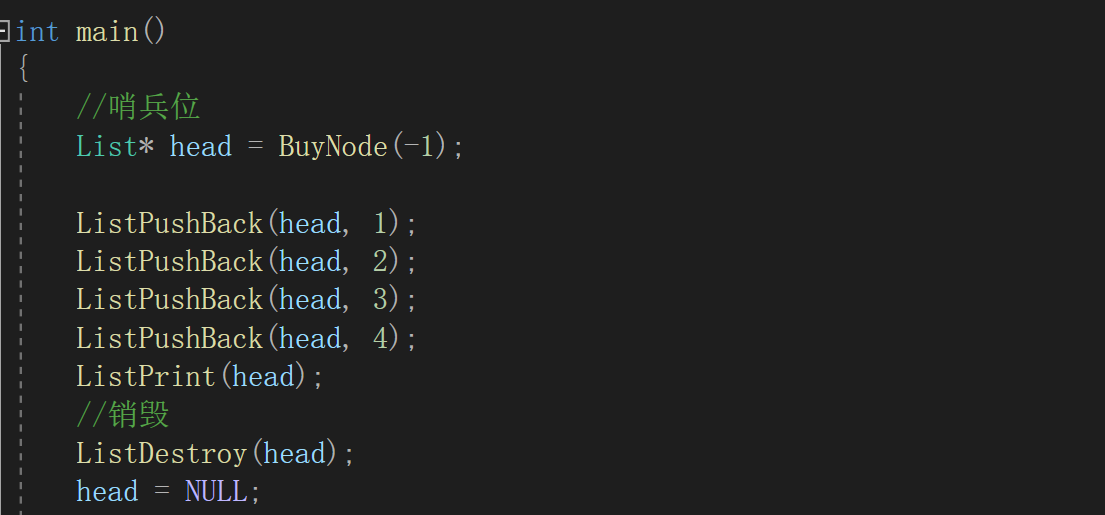
数据结构:双向链表
文章目录 1. 双向带头循环链表的结构2. 相关操作2.1 创建节点2.2 尾插2.3 头插2.4 打印2.5 尾删2.6 头删2.7 查找2.8 指定位置前/后插入2.9 删除指定位置的节点2.10 删除指定位置后的节点2.11 销毁链表 3.顺序表与链表区别 1. 双向带头循环链表的结构 与单链表不同的是…...

51单片机之数码管显示表白数字篇
朝菌不知晦朔 蟪蛄不知春秋 眼界决定境界 CSDN 请求进入专栏 是否进入《51单片机专栏》? 确定 目录 数码管的简介 数码管引脚定义 数码管的原理图 74HC245 代码实现 静态数码管的显示 动态数码管的显示 数码管实现表白画面 数码管的简介 L…...
代码随想录算法训练营DAY16 | 二叉树 (3)
一、LeetCode 104 二叉树的最大深度 题目链接:104.二叉树的最大深度https://leetcode.cn/problems/maximum-depth-of-binary-tree/ 思路:采用后序遍历递归求解。 class Solution {int ans 0;public int maxDepth(TreeNode root) {if(root null){retur…...

springboot(ssm大学生计算机基础网络教学系统 在线课程系统Java系统
springboot(ssm大学生计算机基础网络教学系统 在线课程系统Java系统 开发语言:Java 框架:springboot(可改ssm) vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mys…...

前端架构: 脚手架的开发流程和常用框架
脚手架的开发流程 脚手架的创建 $ npm init 脚手架的开发 分包 分包是指当我们一个脚手架比较复杂的时候,不可能把所有的js代码全部写在一个脚手架当中势必会把它建很多的不同的模块 package,通常我们会把它称之为一个分包的过程会和实际的这个项目一样…...
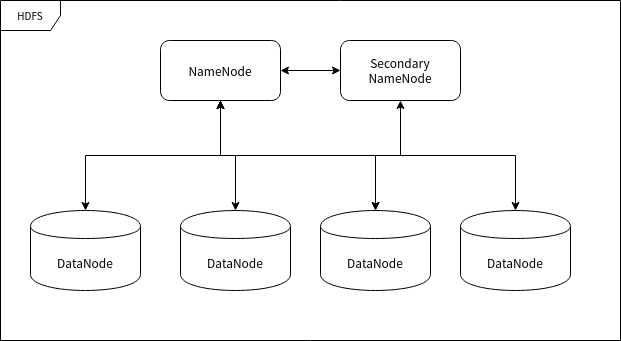
3.0 Hadoop 概念
本章着重介绍 Hadoop 中的概念和组成部分,属于理论章节。如果你比较着急可以跳过。但作者不建议跳过,因为它与后面的章节息息相关。 Hadoop 整体设计 Hadoop 框架是用于计算机集群大数据处理的框架,所以它必须是一个可以部署在多台计算机上…...

mysql 对于null字段排序处理
最近遇到一个需求 ,需要对一个报表的多个字段进行多字段复杂条件排序 排序字段为NULL时 Mysql对于排序字段为NULL时,有自身默认的排序规则,默认是认为null 值 是无穷小 ELECT id,script_id,last_modified,live_count,next_show FROM virtua…...

NLP_语言模型的雏形 N-Gram 模型
文章目录 N-Gram 模型1.将给定的文本分割成连续的N个词的组合(N-Gram)2.统计每个N-Gram在文本中出现的次数,也就是词频3.为了得到一个词在给定上下文中出现的概率,我们可以利用条件概率公式计算。具体来讲,就是计算给定前N-1个词时࿰…...

mac电脑flutter环境配置,解决疑难问题
准备工作 首先搭建flutter的环境需要使用到flutter的sdk,可以直接跳去官网下载:Choose your first type of app - Flutter 中文文档 - Flutter 中文开发者网站 - Flutter,下载时要注意你电脑所使用的芯片是Intel的还是苹果的芯片。 下载好的…...

C++ bool 布尔类型
在C 中 bool类型占用1个字节长度,bool 类型只有两个取值,true 和 false,true 表示“真”,false 表示“假”。 需要注意的C中使用cout 打印的时候是没有true 和 false 的 只有0和1 ,这里0表示假,非0表示真 …...
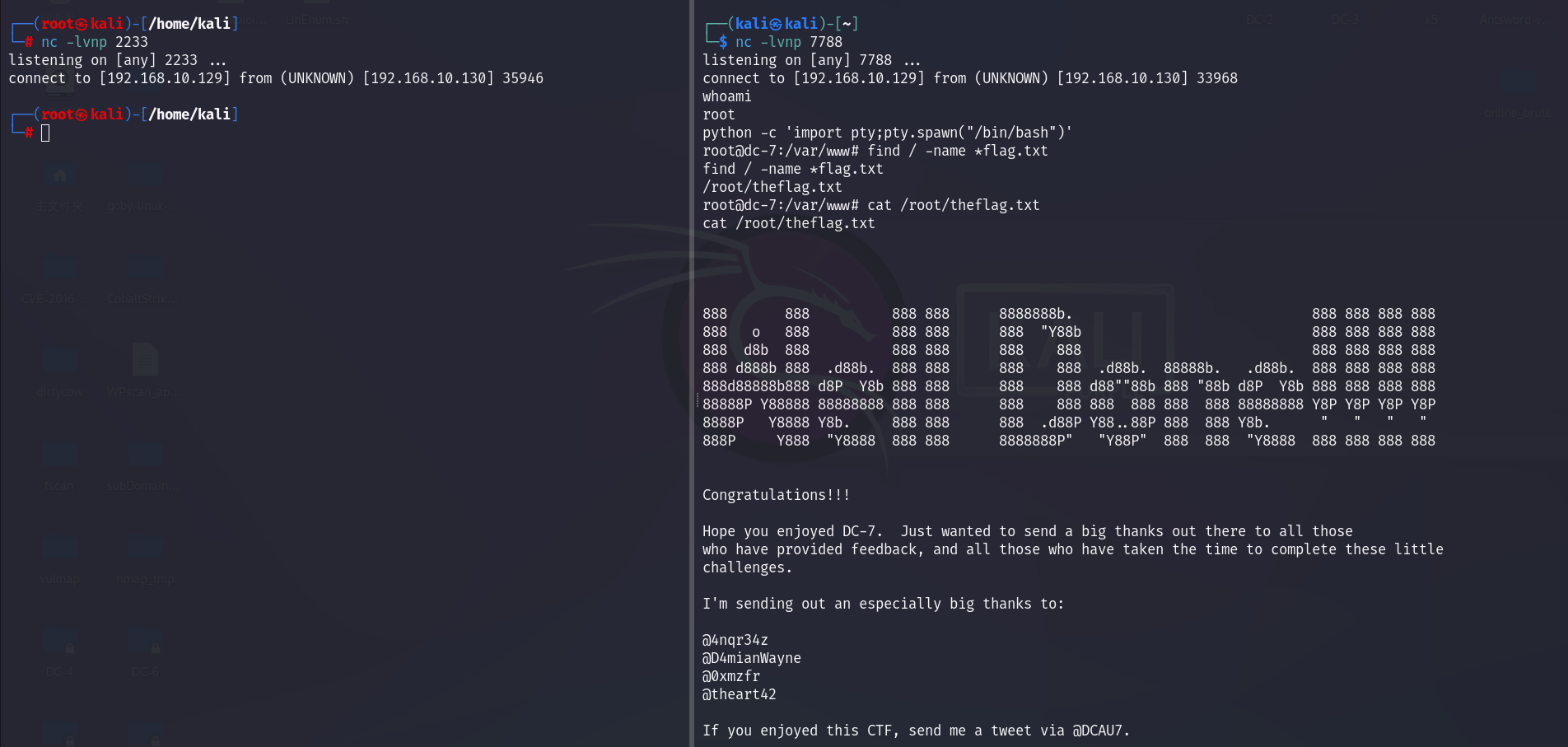
DC-7靶机渗透详细流程
信息收集: 1.存活扫描: 由于靶机和kali都是nat的网卡,都在一个网段,我们用arp-scan会快一点: arp-scan arp-scan -I eth0 -l └─# arp-scan -I eth0 -l Interface: eth0, type: EN10MB, MAC: 00:0c:29:dd:ee:6…...

提速MySQL:数据库性能加速策略全解析
提速MySQL:数据库性能加速策略全解析 引言理解MySQL性能指标监控和评估性能指标索引优化技巧索引优化实战案例 查询优化实战查询优化案例分析 存储引擎优化InnoDB vs MyISAM选择和优化存储引擎存储引擎优化实例 配置调整与系统优化配置调整系统优化优化实例 实战案例…...
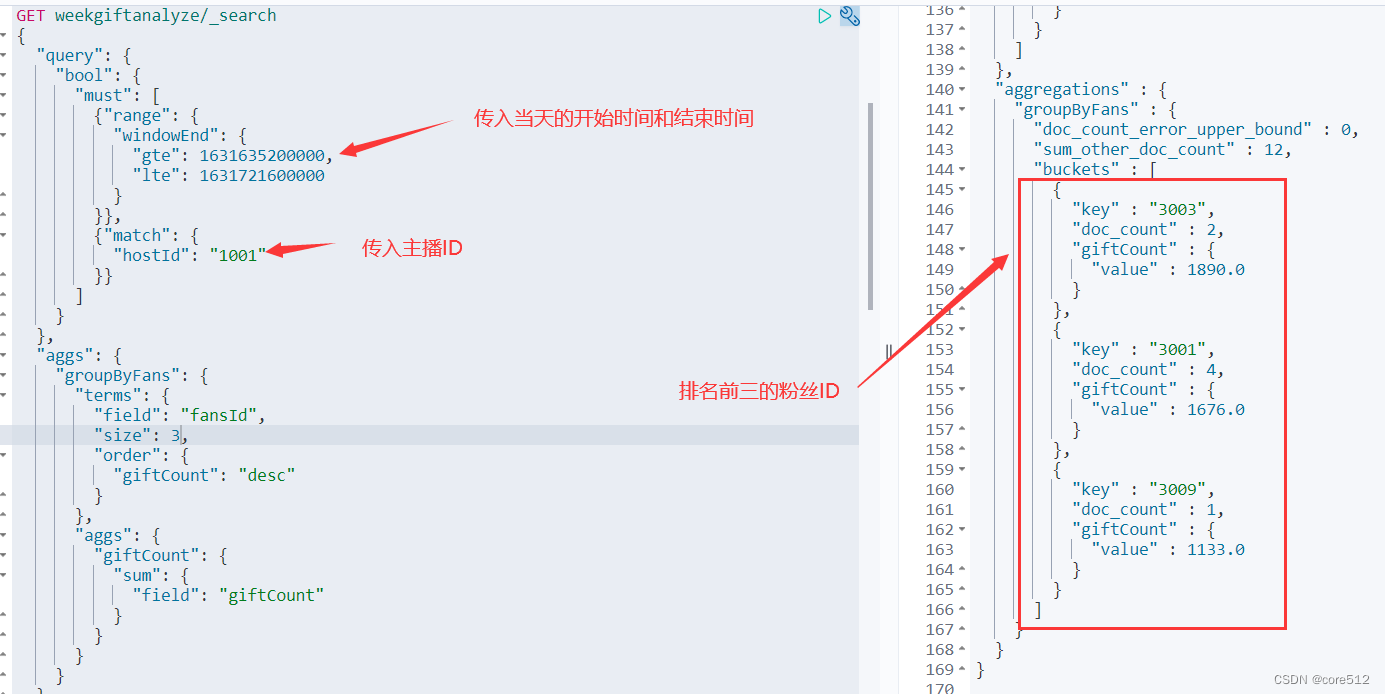
Flink实战六_直播礼物统计
接上文:Flink实战五_状态机制 1、需求背景 现在网络直播平台非常火爆,在斗鱼这样的网络直播间,经常可以看到这样的总榜排名,体现了主播的人气值。 人气值计算规则:用户发送1条弹幕互动,赠送1个荧光棒免费…...
 | Scaffold - 脚手架)
Compose | UI组件(十五) | Scaffold - 脚手架
文章目录 前言一、Scaffold脚手架简介二、Scaffold的主要组件三、如何使用Scaffold四、Compose中Scaffold脚手架的具体例子例子1:基本Scaffold布局例子2:带有Drawer的Scaffold布局例子3:带有Snackbar的Scaffold布局 总结 前言 Compose中的Sca…...

Vue-60、Vue技术router-link的replace属性
1、作用:控制路由跳转时操作浏览器历史记录的模式 2、浏览器的历史记录有两种写入方式:分别是push和replace,push是追加历史记录,replace是替换当前记录。路由跳转时候默认为push 3、如何开启replace模式: <router-link rep…...

Hive与Presto中的列转行区别
Hive与Presto列转行的区别 1、背景描述2、Hive/Spark列转行3、Presto列转行 1、背景描述 在处理数据时,我们经常会遇到一个字段存储多个值,这时需要把一行数据转换为多行数据,形成标准的结构化数据 例如,将下面的两列数据并列转换…...

探讨CSDN等级制度:博客等级、原力等级、创作者等级
个人名片: 🦁作者简介:学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由…...

2.8作业
sqlite3数据库操作接口详细整理,以及常用的数据库语句 头文件: #include <sqlite3.h> 编译时候要加上-lsqlite3 gcc a.c -lsqlite3 1)sqlite3_open 打开一个数据库,如果数据库不存在,则创建一个数据库 2&am…...

机器学习中常用的性能度量—— ROC 和 AUC
什么是泛化能力? 通常我们用泛化能力来评判一个模型的好坏,通俗的说,泛化能力是指一个机器学期算法对新样本(即模型没有见过的样本)的举一反三的能力,也就是学以致用的能力。 举个例子,高三的…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
