数字图像处理实验记录八(图像压缩实验)
前言:做这个实验的时候很忙,就都是你抄我我抄你了
一、基础知识
1.为什么要进行图像压缩:
图像的数据量巨大,对计算机的处理速度、存储容量要求高。传输信道带宽、通信链路容量一定,需要减少传输数据量,提高通信速度。因此要进行图像压缩,减少数据量。
2.怎么进行图像压缩:
我们使用霍夫曼编码进行压缩。霍夫曼编码原理是利用信息符号概率分布特性的变字长的编码方法。对于出现概率大的信息符号编以短字长的码,对于出现概率小的信息符号编以长字长的码。


二、实验要求
1.读入一幅灰度图像,计算该图像的平均信息量-熵。
(备注:可以读入小一些的图像,例如256256,512512的。)
2.使用霍夫曼编码的方法,对该图像进行压缩。
3. 计算编码后的平均码长及压缩比。
三、实验记录
任务1:
读入一幅灰度图像,计算该图像的平均信息量-熵。
(备注:可以读入小一些的图像,例如256256,512512的。)
%求一幅图像的熵值
clc
clear
close all
I=imread('Acat.png');
I = rgb2gray(I);G=256; %图像的灰度级
[height,width] = size(I); %获取输入值的高和宽
[count,x] = imhist(I,G);
p = count; %原始灰度直方图
I_size = height*width;
H_x = 0;
for i=1:256 %循环p(i) = count(i)/I_size;if p(i)~=0; %如果像素点的概率不为零H_x=-p(i)*log2(p(i))+H_x; %求熵值的公式end
end
H_x %显示熵值
任务2:
使用霍夫曼编码的方法,对该图像进行压缩。
[M,N] = size(I);%将图像转为二维矩阵
I1 = I(:);%转为一维向量
k = 0:255;
dict = huffmandict(k,p); %根据灰度级k和概率数组P生成Huffman字典
enco = huffmanenco(I1,dict);
deco = huffmandeco(enco,dict); %哈夫曼解码
Ide = col2im(deco,[M,N],[M,N],'distinct'); %把向量重新转换成图像块;
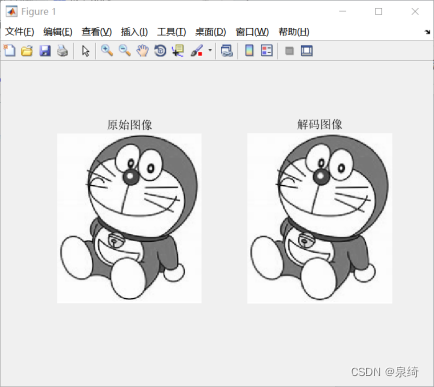
subplot(1,2,1);imshow(I);title('原始图像');
subplot(1,2,2);imshow(uint8(Ide));title('解码图像');
任务3:
计算编码后的平均码长及压缩比。
B=length(enco);
sumcode=length(deco);%编码后比特长度
CR=sumcode/B;%计算压缩率
disp(['原始图像 Bit: ',num2str(B),' bit']);
disp(['压缩图像 Bit: ',num2str(sumcode),' bit']);
disp(['压缩率: ',num2str(CR)]);
四、实验结果
任务1:
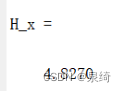
任务2:
任务3:

相关文章:

数字图像处理实验记录八(图像压缩实验)
前言:做这个实验的时候很忙,就都是你抄我我抄你了 一、基础知识 1.为什么要进行图像压缩: 图像的数据量巨大,对计算机的处理速度、存储容量要求高。传输信道带宽、通信链路容量一定,需要减少传输数据量&a…...
navigator.mediaDevices.getUserMedia获取本地音频/麦克权限并提示用户
navigator.mediaDevices.getUserMedia获取本地音频/麦克权限并提示用户 效果获取权限NotFoundErrorNotAllowedError 代码 效果 获取权限 NotFoundError NotAllowedError 代码 // 调用 captureLocalMedia()// 方法 function captureLocalMedia() {console.warn(Requesting lo…...

CTF-show WEB入门--web19
今晚web19也就顺便解决了 老样子我们先打开题目看看题目提示: 可以看到题目提示为: 密钥什么的,就不要放在前端了 然后我们打开题目链接: 然后我们查看网页源代码: 可以发现有用的内容全在网页源代码里。 前端验证…...

04 使用gRPC实现客户端和服务端通信
使用gRPC实现客户端和服务端通信 参考文档: 基于C#的GRPC 1 创建项目和文件夹 GrpcClientDemoGrpcServerDemoProtos解决方案和文件夹1.1 添加nuget依赖 客户端和服务器都要有依赖和gRPC_Objects文件夹 <ItemGroup><PackageReference Include"Google.Protobu…...
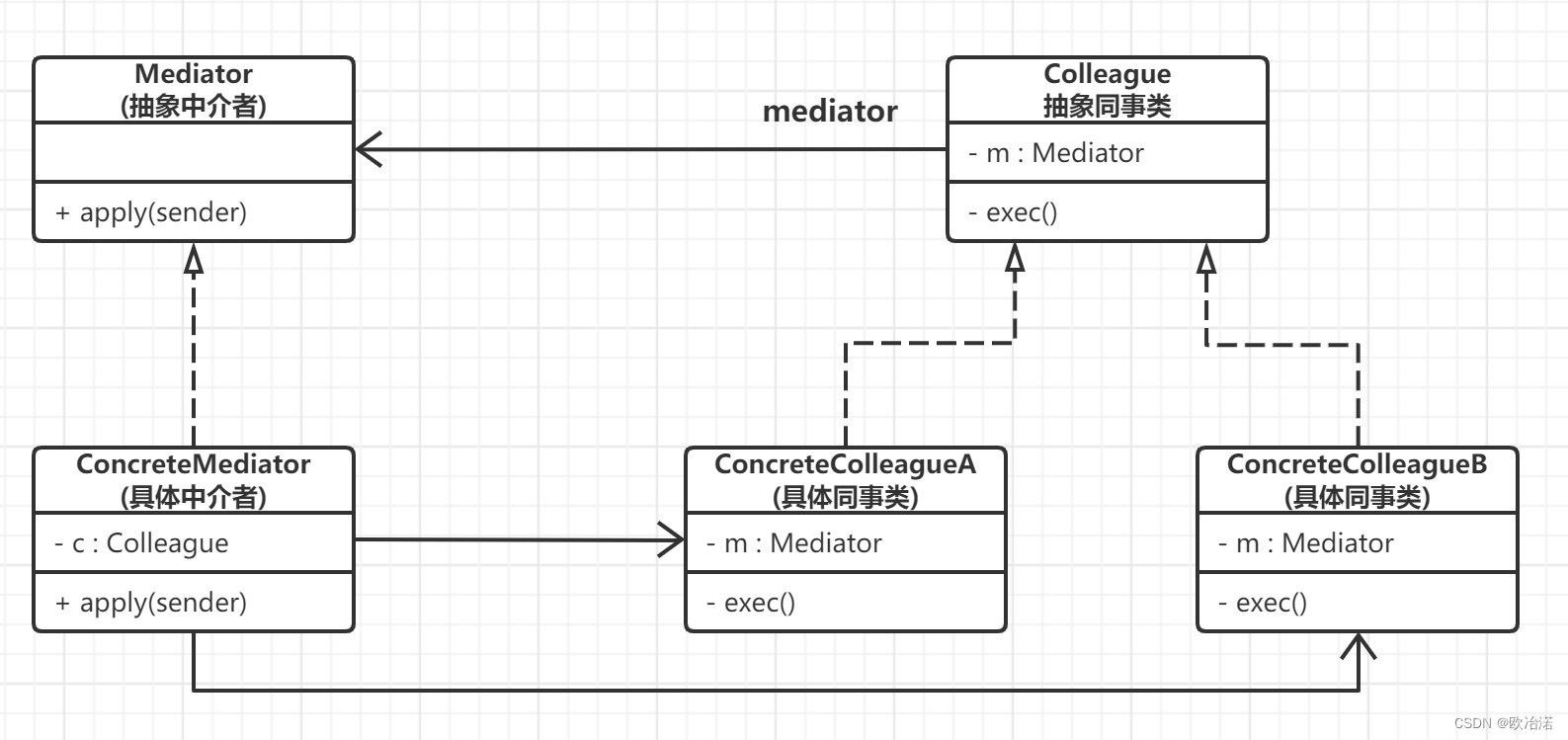
设计模式-行为型模式(下)
1.访问者模式 访问者模式在实际开发中使用的非常少,因为它比较难以实现并且应用该模式肯能会导致代码的可读性变差,可维护性变差,在没有特别必要的情况下,不建议使用访问者模式. 访问者模式(Visitor Pattern) 的原始定义是: 允许在运行时将一个或多个操作应用于一…...

华为交换机常用命令
一、查看命令 1、查看交换机信息 display version 查看交换机软件版本display clock 查看交换机时钟2、查看交换机配置 display saved-configuration 显示系统保存配置display current-configuration 显示系统当前配置 3、查看当前对象信息 display this …...

【Linux】信号-上
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 🏠个人专栏:题目解析 🌎推荐文章:【LeetCode】winter vacation training 目录 👉🏻信号的概念与产生jobs命令普通信号和实…...

uniapp 开发App 权限授权 js-sdk
从官网的插件市场下载的: 直接上代码: /*** 本模块封装了Android、iOS的应用权限判断、打开应用权限设置界面、以及位置系统服务是否开启*/var isIos // #ifdef APP-PLUS isIos (plus.os.name "iOS") // #endif// 判断推送权限是否开启 fu…...
【01】判断素数/质数(C语言)
目录 (1)素数特点:只能被1和本身整除 (2)代码如下: (3)运行结果如下 编辑 (4)函数引申 (1)素数特点:只能被1和本身…...
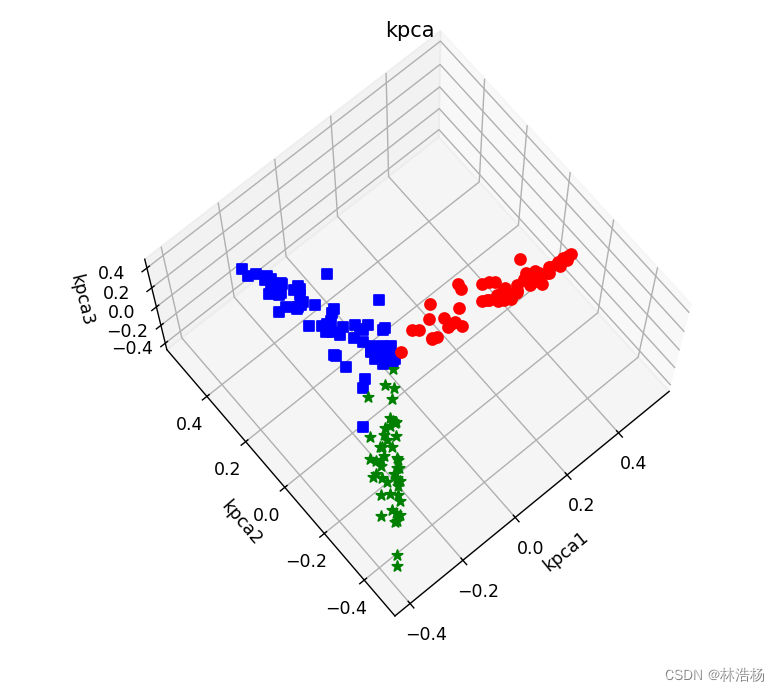
特征工程:特征提取和降维-上
目录 一、前言 二、正文 Ⅰ.主成分分析 Ⅱ.核主成分分析 三、结语 一、前言 前面介绍的特征选择方法获得的特征,是从原始数据中抽取出来的,并没有对数据进行变换。而特征提取和降维,则是对原始数据的特征进行相应的数据变换,并…...

前端JavaScript篇之强类型语言和弱类型语言的区别和对比
目录 强类型语言和弱类型语言的区别和对比总结 强类型语言和弱类型语言的区别和对比 强类型语言和弱类型语言是编程语言的两种不同类型系统,它们处理变量类型的方式有所不同。 强类型语言: 强类型语言要求在使用变量之前必须明确声明其类型,…...
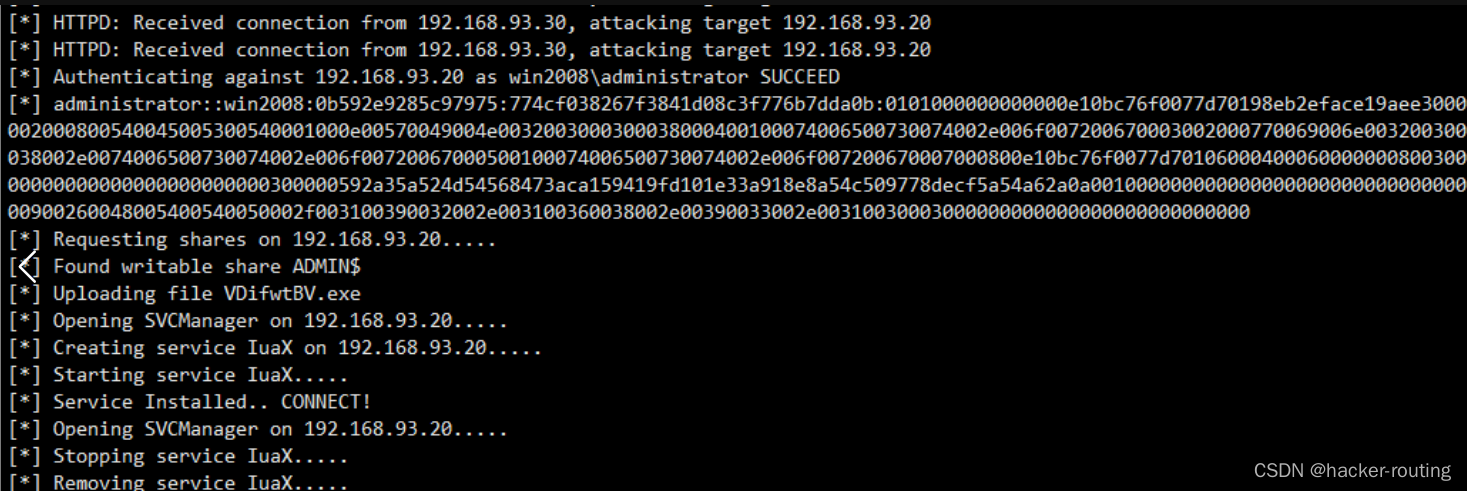
[红日靶机渗透] ATKCK红队评估实战靶场三
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【ATK&CK红队评估实战靶场】 【VulnHub靶场复现】【面试分析】 …...
)
网课:N皇后问题——牛客(题解和疑问)
题目描述 给出一个nnn\times nnn的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。 输入描述: …...
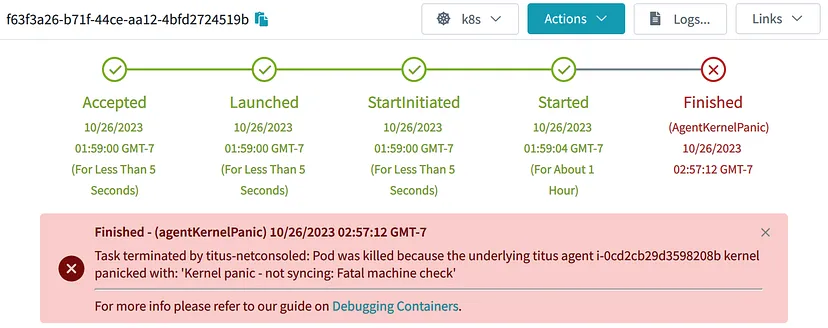
[大厂实践] Netflix容器平台内核panic可观察性实践
在某些情况下,K8S节点和Pod会因为出错自动消失,很难追溯原因,其中一种情况就是发生了内核panic。本文介绍了Netflix容器平台针对内核panic所做的可观测性增强,使得发生内核panic的时候,能够导出信息,帮助排…...

2024/2/8
数据类型与作用域练习 1、选择题 1.1、以下选项中,不能作为合法常量的是 ___b_______ A)1.234e04 B)1.234e0.4 C)1.234e4 D)1.234e0 1.2、以下定义变量并初始化错误的是______d_______。 A) char c1 ‘H’ &am…...
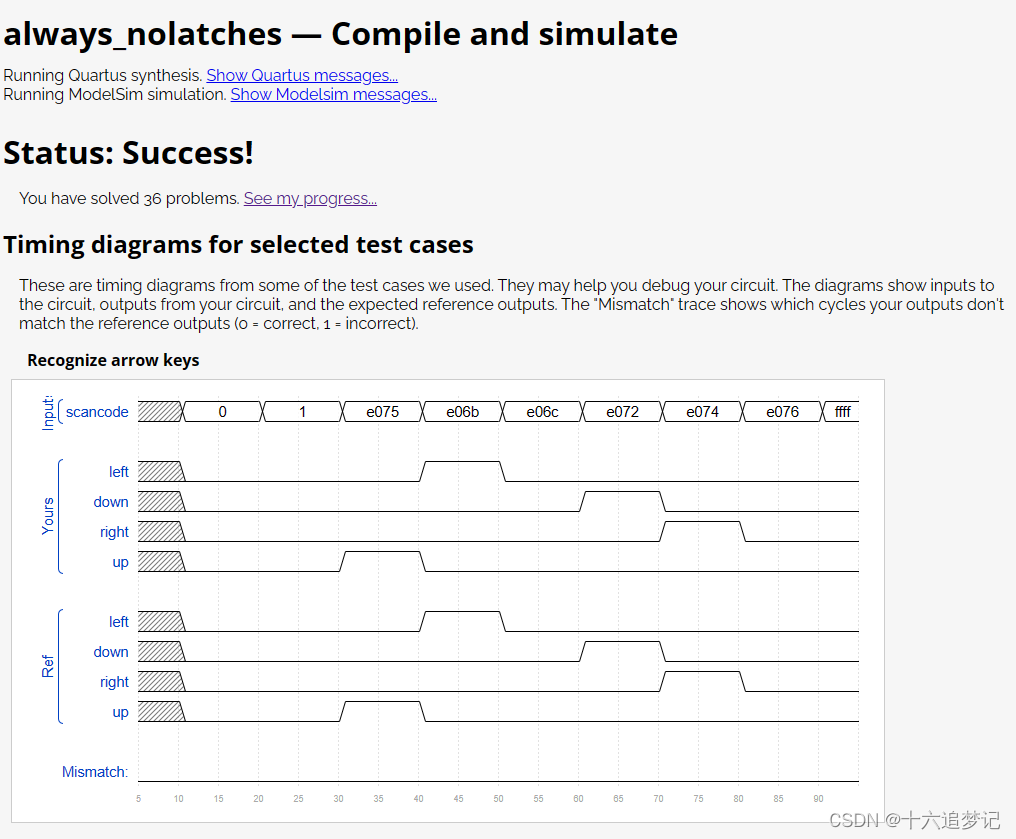
Verilog刷题笔记23
题目: Suppose you’re building a circuit to process scancodes from a PS/2 keyboard for a game. Given the last two bytes of scancodes received, you need to indicate whether one of the arrow keys on the keyboard have been pressed. This involves a fairly simp…...
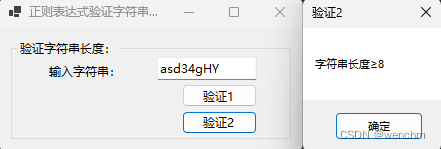
C#验证字符串的长度,用正则表达式 vs 字符数组长度或字符串的长度
目录 一、使用的方法 1.使用正则表达式 2.通过计算字符串的长度验证 二、实例 1.源码 2.生成效果 一、使用的方法 1.使用正则表达式 使用正则表达式可以判断和限制用户输入的字符串长度。 比如验证用户密码不得少于8为,匹配的正则表达式"^.{8,}$"…...

opencv C++ dnn模块调用yolov5以及Intel RealSense D435深度相机联合使用进行目标检测
一、代码 #include <opencv2/opencv.hpp> #include <opencv2/dnn/dnn.hpp> #include <librealsense2/rs.hpp> // Include RealSense Cross Platform APIusing namespace cv; using namespace dnn; using namespace std; using namespace rs2;// 类名数组&am…...
2024牛客寒假算法基础集训营1(视频讲解全部题目)
2024牛客寒假算法基础集训营1(题目全解) ABCDEFGHIJKLM 2024牛客寒假算法基础集训营1(视频讲解全部题目) A #include<bits/stdc.h> #define endl \n #define deb(x) cout << #x << " " << …...

第三百一十三回
文章目录 1. 概念介绍2. 实现方法2.1 obscureText属性2.2 decoration属性 3. 示例代码4. 内容总结 我们在上一章回中介绍了"如何实现倒计时功能"相关的内容,本章回中将介绍如何实现密码输入框.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
