P3647 题解
文章目录
- P3647 题解
- Overview
- Description
- Solution
- Lemma
- Proof
- Main
- Code
P3647 题解
Overview
很好的题,但是难度较大。
模拟小数据!——【数据删除】
Description
给定一颗树,有边权,已知这棵树是由这两个操作得到的:
Append(u, w):在 u u u 和 w w w 之间连一条红边,注意这里的 w w w 必须是新点。Insert(u, v, w):在 u u u 和 w w w, v v v 和 w w w 之间各连一条蓝边,注意这里的 w w w 必须是新点。
问蓝线的长度最大能到多少。
Solution
我们可以尝试将所有的 Insert 所产生的蓝边对都提取出来。
它们只可能有两种形式:son - u - father 和 son1 - u - son2。
Lemma
引理:所有的蓝边都可以在某一个根上表现出形如 son - u - father 的形式。
Proof
当树上没有形如 son1 - u - son2 的蓝边时,显然成立;
当树上恰好有一个形如 son1 - u - son2 的蓝边时,可以将 son1 和 son2 其中之一作为根,解决问题;
当树上有大于一个形如 son1 - u - son2 的蓝边时,可以证明不存在这样的边。
如图,当存在形如 1 的情况时,son1 和 son2 构成了单独的连通块,因为如果不是,那么 son1 和 son2 一定会是父子关系,矛盾;
当存在多个这样的连通块时,如图 2,建树时节点一定会组成单一的连通块,因为 u u u 总是存在,所以不成立。
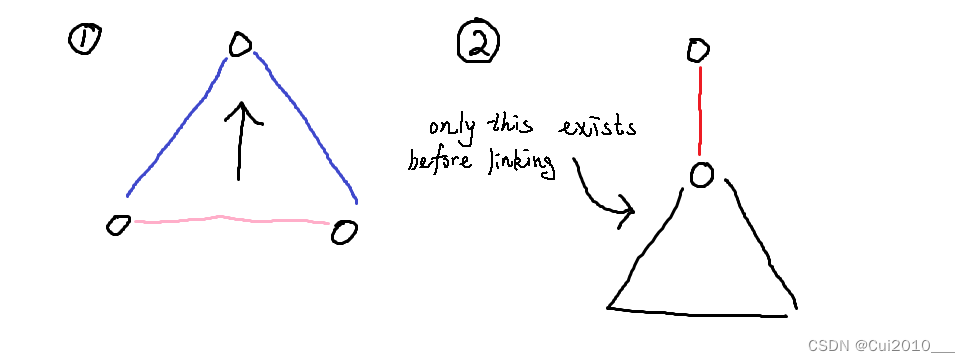
Main
有了引理,就可以树形 dp 了。
枚举树根,对每个根 DP。设 d u , 0 / 1 d_{u,0/1} du,0/1 为 u u u 为根, u u u 是否为蓝边终点的子树最大边权和。
先看 d u , 0 d_{u,0} du,0,因为没有边上的限制,所以可以任意取,对于是中点的情况,可以再加上边权 w ( u , v ) w(u,v) w(u,v),即 max ( d v , 1 + w ( u , v ) , d v , 0 ) \max(d_{v,1}+w(u,v), d_{v,0}) max(dv,1+w(u,v),dv,0)。
再看 d u , 1 d_{u,1} du,1,一定有一个 d v , 0 + w ( u , v ) d_{v,0}+w(u,v) dv,0+w(u,v),其它都是 max ( d v , 1 + w ( u , v ) , d v , 0 ) \max(d_{v,1}+w(u,v), d_{v,0}) max(dv,1+w(u,v),dv,0),所以要加上 max Δ sum \max \Delta_{\text{sum}} maxΔsum。
所以关于 d d d 的状态转移方程可以这样写:
d u , 0 = ∑ v ∈ son ( u ) max ( d v , 1 + w ( u , v ) , d v , 0 ) d u , 1 = d u , 0 + max v ∈ son ( u ) { d v , 0 + w ( u , v ) − max ( d v , 1 + w ( u , v ) , d v , 0 ) } d_{u,0} = \sum_{v\in \text{son}(u)}\max(d_{v,1}+w(u,v),d_{v,0})\\d_{u,1} = d_{u,0}+\max_{v\in \text{son}(u)}\{d_{v,0} + w(u,v) - \max(d_{v,1} + w(u,v), d_{v,0})\} du,0=v∈son(u)∑max(dv,1+w(u,v),dv,0)du,1=du,0+v∈son(u)max{dv,0+w(u,v)−max(dv,1+w(u,v),dv,0)}
这样,就可以枚举根得到 O ( n 2 ) O(n^2) O(n2) 的复杂度, 15 pts 15\text{pts} 15pts。
接下来考虑换根 DP。
一张图解释接下来两个 DP 数组的含义。
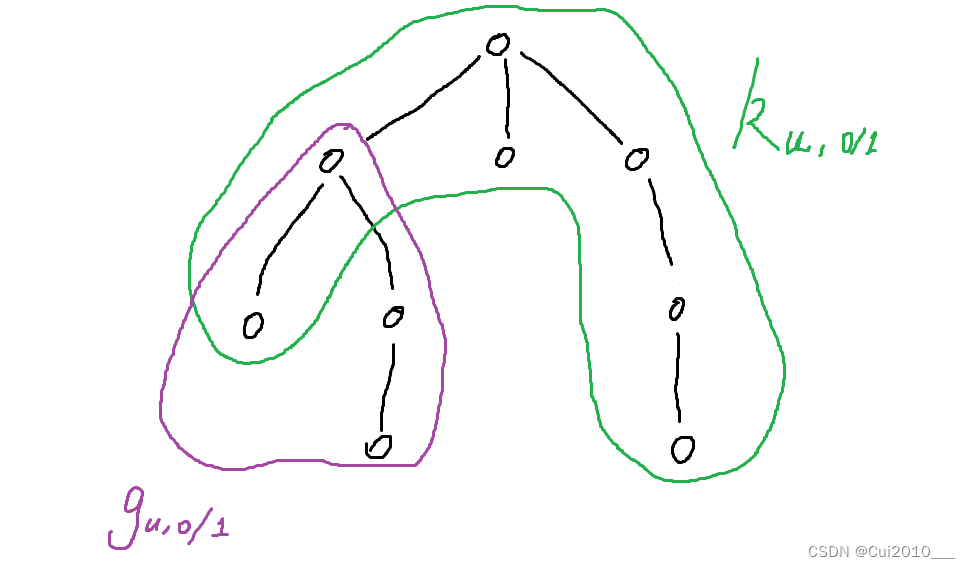
这里的 g g g 并不描述这个子树,而是以 u u u 为根的整棵树。
根据 f f f 的转移方程,我们照样也可以推出 g g g 和 k k k 的转移方程,留给读者思考。
注意到方程里仍有大量之前可以利用的内容,所以需要维护最大值和次大值。
Code
#include <bits/stdc++.h>using namespace std;int dp[200001][2], dp1[200001][2], dp2[200001][2], mx[200001], mx2[200001];vector<pair<int, int> > gv[200001];inline void add_edge(int u, int v, int w){gv[u].push_back(make_pair(v, w));gv[v].push_back(make_pair(u, w));
}void dfs(int u, int fa){vector<int> vec;vec.push_back(INT_MIN), vec.push_back(INT_MIN);for(auto v : gv[u]){if(v.first == fa) continue;dfs(v.first, u);dp[u][0] += max(dp[v.first][0], dp[v.first][1] + v.second);vec.push_back(dp[v.first][0] + v.second - max(dp[v.first][0], dp[v.first][1] + v.second));}sort(vec.begin(), vec.end(), greater<int>());mx[u] = vec[0], mx2[u] = vec[1];dp[u][1] = dp[u][0] + mx[u];
}void dfs1(int u, int fa, int lst){for(auto v : gv[u]){if(v.first == fa) continue;int tmp = dp[v.first][0] + v.second - max(dp[v.first][0], dp[v.first][1] + v.second);dp2[u][0] = dp1[u][0] - max(dp[v.first][0], dp[v.first][1] + v.second);dp2[u][1] = dp2[u][0] + (mx[u] == tmp ? mx2[u] : mx[u]);if(fa + 1) dp2[u][1] = max(dp2[u][1], dp2[u][0] + dp2[fa][0] + lst - max(dp2[fa][0], dp2[fa][1] + lst));dp1[v.first][0] = dp[v.first][0] + max(dp2[u][0], dp2[u][1] + v.second);
// dp1[v.first][1] = dp1[v.first][0] + max(mx[v.first], dp2[u][0] + v.second - max(dp2[u][0], dp2[u][1] + v.second));dfs1(v.first, u, v.second);}
}void init_vars(){// type your initiating code...
}void solve(int testcase, ...){init_vars();int n; cin >> n;for(int i = 0; i < n - 1; i++){int u, v, w; cin >> u >> v >> w;add_edge(u, v, w);}dfs(1, -1); dp1[1][0] = dp[1][0];dfs1(1, -1, 0);int ans = 0;for(int i = 1; i <= n; i++){//cout << mx[i] << " " << mx2[i] << endl;ans = max(ans, dp1[i][0]);}cout << ans << endl;
}signed main(){
#ifdef filesfreopen(".in", "r", stdin);freopen(".out", "w", stdout);
#endifios::sync_with_stdio(0);cin.tie(0), cout.tie(0);solve(1);
#ifdef filesfclose(stdin); fclose(stdout);
#endifreturn 0;
}/** things to check* 1. int overflow or long long memory need* 2. recursion/array/binary search/dp/loop bounds* 3. precision* 4. special cases(n=1,bounds)* 5. delete debug statements* 6. initialize(especially multi-tests)* 7. = or == , n or m ,++ or -- , i or j , > or >= , < or <=* 8. keep it simple and stupid* 9. do not delete, use // instead* 10. operator priority* 11. is there anything extra to output?* 12. THINK TWICE CODE ONCE, THINK ONCE DEBUG FOREVER* 13. submit ONCE, AC once. submit twice, WA forever* 14. calm down and you'll get good rank* 15. even a bit wrong scores zero* 16. ...**//** something to think about* 1. greedy? dp? searching? dp with matrix/ segment tree? binary search? ...?* 2. If it is difficult, why not the opposite?**//*########## ############ ##### ######### ##### #### ####
#### ##### #### ####
#### ########## #### ####
#### ##### #####
#### ##### ######### ##### ################ ############# #####
*/相关文章:

P3647 题解
文章目录 P3647 题解OverviewDescriptionSolutionLemmaProof Main Code P3647 题解 Overview 很好的题,但是难度较大。 模拟小数据!——【数据删除】 Description 给定一颗树,有边权,已知这棵树是由这两个操作得到的࿱…...
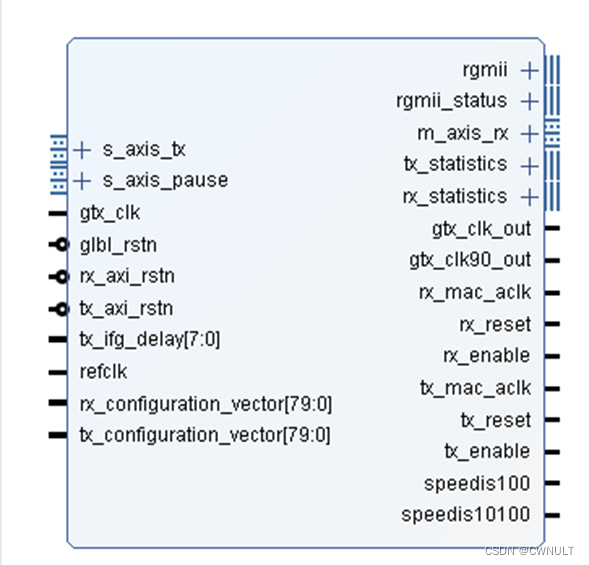
Vivado Tri-MAC IP的例化配置(三速以太网IP)
目录 1 Tri-MAC IP使用RGMII接口的例化配置1.1 Data Rate1.2 interface配置1.3 Shared Logic配置1.4 Features 2 配置完成IP例化视图 1 Tri-MAC IP使用RGMII接口的例化配置 在网络设计中,使用的IP核一般为三速以太网IP核,使用时在大多数场景下为配置为三…...
交友系统---让陌生人变成熟悉人的过程。APP小程序H5三端源码交付,支持二开。
随着社交网络的发展和普及,人们之间的社交模式正在发生着深刻的变革。传统的线下交友方式已经逐渐被线上交友取而代之。而同城交友正是这一趋势的产物,它利用移动互联网的便利性,将同城内的人们连接在一起,打破了时空的限制&#…...

uni-app 经验分享,从入门到离职(三)——关于 uni-app 生命周期快速了解上手
文章目录 📋前言⏬关于专栏 🎯什么是生命周期🧩应用生命周期📌 关于 App.vue/App.uvue 🧩页面生命周期📌关于 onShow 与 onLoad 的区别 🧩组件生命周期 📝最后 📋前言 这…...

PostgreSQL 与 MySQL 相比,优势何在?
我们将通过一张对比表格详细列出 PostgreSQL 与 MySQL 在不同方面的对比: 对比表格 特性/数据库PostgreSQLMySQL数据类型支持支持JSON/JSONB、数组、区间等高级数据类型基本数据类型支持,JSON支持较普通遵循SQL标准更严格遵循,支持复杂查询…...

Linux(三)--文件系统
Linux命令简介 [rootlocalhost ~]# 表示 Linux 系统的命令提示符。 []:这是提示符的分隔符号,没有特殊含义。 root:显示的是当前的登录用户,笔者现在使用的是 root 用户登录。 :分隔符号,没有特殊含义。 l…...
DC-8靶机渗透详细流程
信息收集: 1.存活扫描: arp-scan -I eth0 -l └─# arp-scan -I eth0 -l Interface: eth0, type: EN10MB, MAC: 00:0c:29:dd:ee:6a, IPv4: 192.168.10.129 Starting arp-scan 1.10.0 with 256 hosts (https://github.com/royhills/arp-scan) 192.168.10…...
SolidWorks学习笔记——入门知识2
目录 建出第一个模型 1、建立草图 2、选取中心线 3、草图绘制 4、拉伸 特征的显示与隐藏 改变特征名称 5、外观 6、渲染 建出第一个模型 1、建立草图 图1 建立草图 按需要选择基准面。 2、选取中心线 图2 选取中心线 3、草图绘制 以对称图形举例,先画出…...
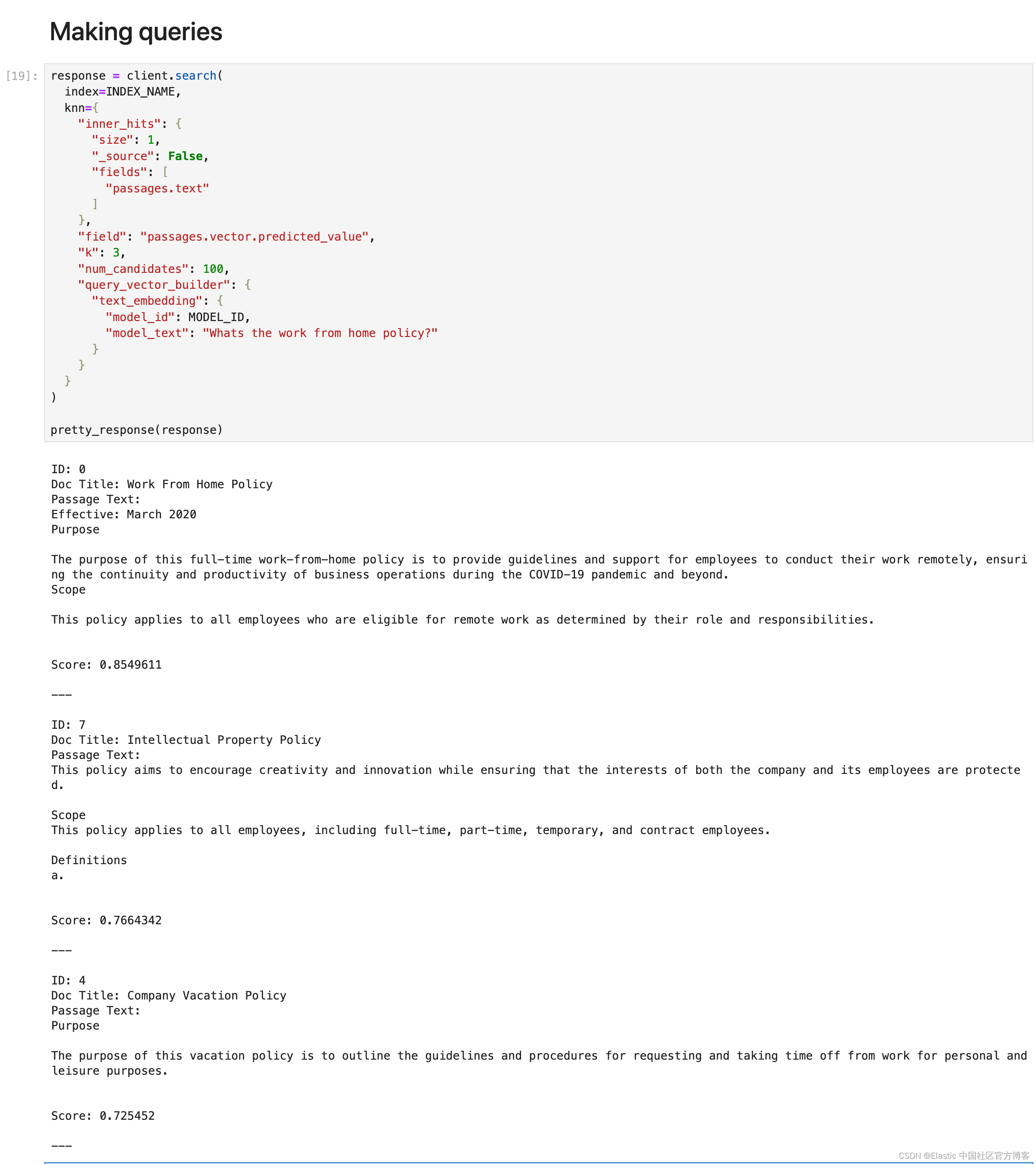
Elasticsearch:通过 ingest pipeline 对大型文档进行分块
在我之前的文章 “Elasticsearch:使用 LangChain 文档拆分器进行文档分块” 中,我详述了如何通过 LangChain 对大的文档进行分块。那个分块的动作是通过 LangChain 在 Python 中进行实现的。对于使用版权的开发者来说,我们实际上是可以通过 i…...
数据库管理-第148期 最强Oracle监控EMCC深入使用-05(20240208)
数据库管理148期 2024-02-08 数据库管理-第148期 最强Oracle监控EMCC深入使用-05(20240208)1 性能主页2 ADDM Spotlight3 实时ADDM4 数据库的其他5 主机总结 数据库管理-第148期 最强Oracle监控EMCC深入使用-05(20240208) 作者&am…...

Bug2- Hive元数据启动报错:主机被阻止因连接错误次数过多
错误代码: 在启动Hive元数据时,遇到了以下错误信息: Caused by: java.sql.SQLException: null, message from server: "Host 192.168.252.101 is blocked because of many connection errors, unblock with mysqladmin flush-hosts&qu…...
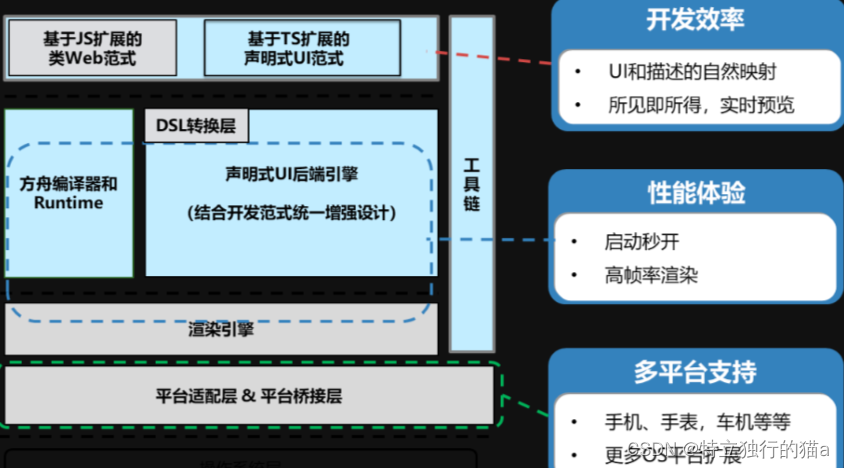
HarmonyOS 鸿蒙应用开发(十、第三方开源js库移植适配指南)
在前端和nodejs的世界里,有很多开源的js库,通过npm(NodeJS包管理和分发工具)可以安装使用众多的开源软件包。但是由于OpenHarmony开发框架中的API不完全兼容V8运行时的Build-In API,因此三方js库大都需要适配下才能用。 移植前准备 建议在适…...

Docker- chapter 1
note 1: docker 利用 volume 进行 presist data。 eg : compose.yaml: volumes:database: //# named db by self list golbal volumes: docker volume ls # the volumes on the disk inpect someone volume: docker volume inspect m…...
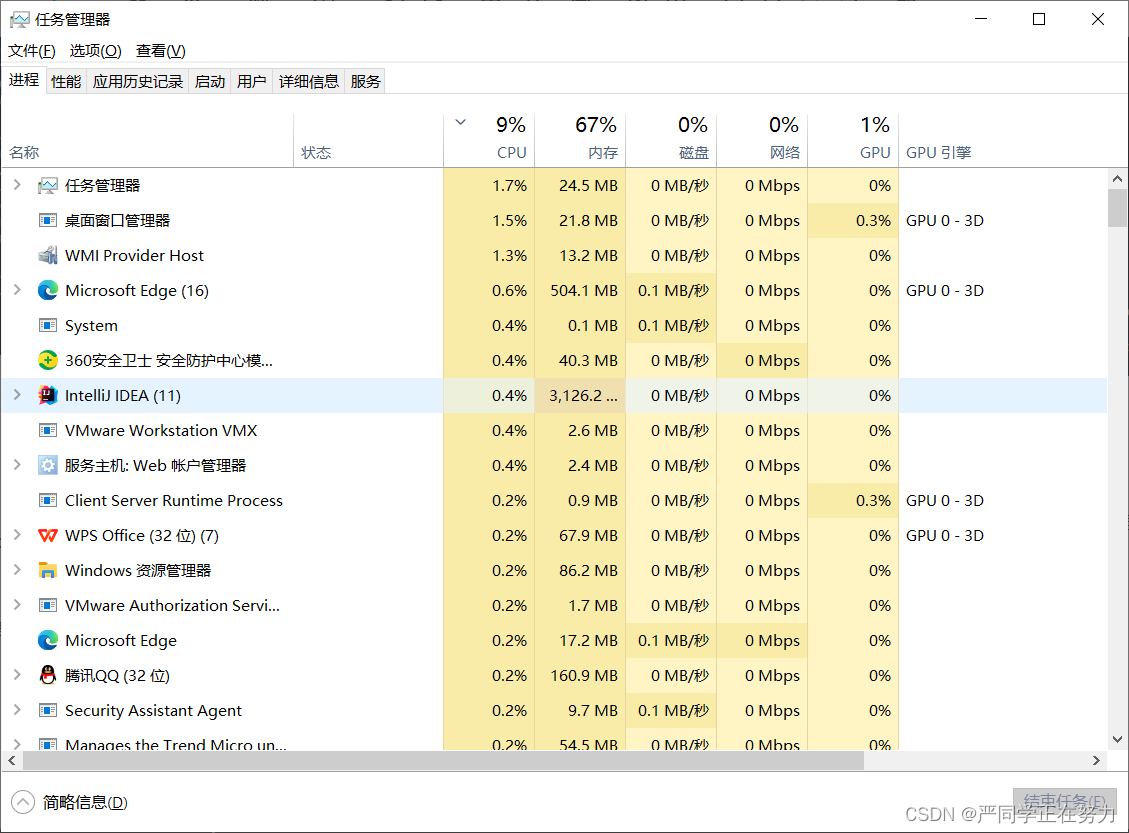
解决IntellIJ Idea内存不足
突然有一天我在IDEA打开两个项目时,发生了报错,说我内存不足,我这电脑内存16G怎么会内存不足。下面是我的解决方案。 IntelliJ IDEA 报告内存不足的原因通常与以下几个因素有关: 项目规模较大:如果您正在开发的项目非…...
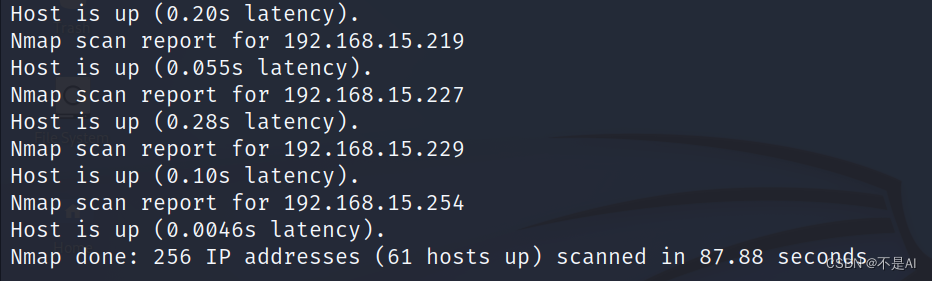
【网络技术】【Kali Linux】Nmap嗅探(二)多设备扫描
上期实验博文:(一)简单扫描 一、实验环境 本次实验进行Nmap多设备扫描,实验使用 Kali Linux 虚拟机(扫描端)、Ubuntu 22.04虚拟机(被扫描端1)、Ubuntu 18.04虚拟机(被扫…...
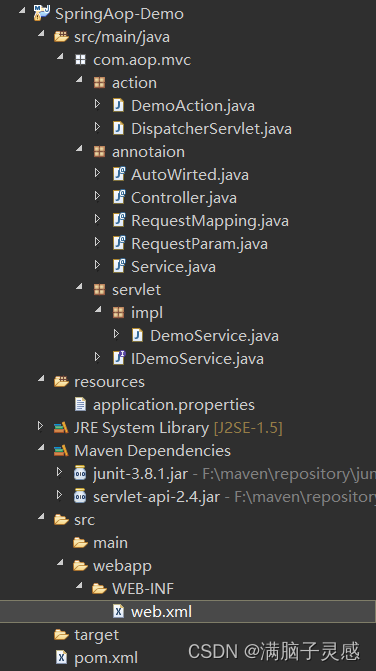
简化版SpringMVC
简化版SpringMVC web.xml xml version"1.0" encoding"UTF-8"?> <web-app version"2.5" xmlns"http://java.sun.com/xml/ns/javaee" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocation&quo…...
Java密码校验(正则表达式):密码由这四种元素组成(数字、大写字母、小写字母、特殊字符),且必须包含全部四种元素;密码长度大于等于8个字符。
1. 需求 对用户密码的强度进行校验,要求用户密码达到一定的强度,符合安全性要求。 1.1. 基础版需求 密码必须由字母和数字组成(同时包括数字和数字);密码长度大于等于8个字符。 1.2. 进阶版需求 密码由这四种元素…...

【AMI】2400 环境安装步骤
2400 环境安装步骤 ----------Ubuntu14.4 MDS4.0 加载代码需要勾上Update Installing SPX related packages sudo apt install gcc-multilib mtd-utils:i386 subversion patch patchutils bison sudo apt install libc6-dev libxml-dom-perl zlib1g zlib1g-dev libcurl4-ope…...

AI:124-基于深度学习的人体遮挡物体重建技术
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的关键代码,详细讲解供…...

23种设计模式之单例模式
目录 什么是单例模式 单例模式的优点 创建单例模式的三大要点 单例模式的实现方式 饿汉模式 懒汉模式 使用场景 什么是单例模式 单例模式是一种创建型设计模式,它的核心思想是保证一个类只有一个实例,并提供一个全局访问点来访问这个实例。 什…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
