DAY39: 动态规划不同路径问题62
Leetcode: 62 不同路径
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
基本思路
1、确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2、确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。所以dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
3、dp数组的初始化
dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
时间复杂度:O(m × n)
空间复杂度:O(m × n)
想不出来的时候,可以想想最后的步骤是由上一步怎么导出的。
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n,0));//初始化二维向量for(int i = 0; i < m; i++){dp[i][0] = 1;//初始化起始} for(int i = 0; i < n; i++){dp[0][i] = 1;}for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){dp[i][j] = dp[i - 1][j]+ dp[i][j - 1];//递推公式}}return dp[m - 1][n - 1];}
};当然也可以使用数论的方法。最后获得组合的方法如下。
但是这道题目要防止两个int相乘出现溢出的情况,所以要对两数相乘做特殊处理。需要在计算分子的时候,不断除以分母。
代码如下
代码随想录
时间复杂度:O(m)
空间复杂度:O(1)
class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1; // 分子int denominator = m - 1; // 分母int count = m - 1;int t = m + n - 2;while (count--) {numerator *= (t--);while (denominator != 0 && numerator % denominator == 0) {numerator /= denominator;denominator--;}}return numerator;}
};Leetcode: 63 不同路径 II
这道题与上道题不一样的点,在于现在的的路径出现了障碍物。
1、dp数组的初始化
dp[i][0]一定都是1,但是如果遇到障碍物,那么后面的所有数组都是0,是无法达到的道路。
2、确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。所以dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。如果出现障碍物,就跳过元素,这样这个元素还是0,那么即使相加相当于只有一个方向的信息。因此我们的递推公式还是dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。遇到障碍物之后都是0。
时间复杂度:O(n × m)
空间复杂度:O(n × m)
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();//注意维度的选择vector<vector<int>> dp(m, vector<int>(n,0));if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for(int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1;for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){if(obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};相关文章:
DAY39: 动态规划不同路径问题62
Leetcode: 62 不同路径 机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。 基本思路 1、确定dp数组(dp table)以及下标的含义 dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条…...
idea开发工具的简单使用与常见问题
1、配置git 选择左上角目录file->setting 打开,Version Control 目录下Git,选择git安装目录下的git.exe文件; 点击test,出现git版本,则表示git识别成功,点击右下角确认即可生效。 2、配置node.js 选…...
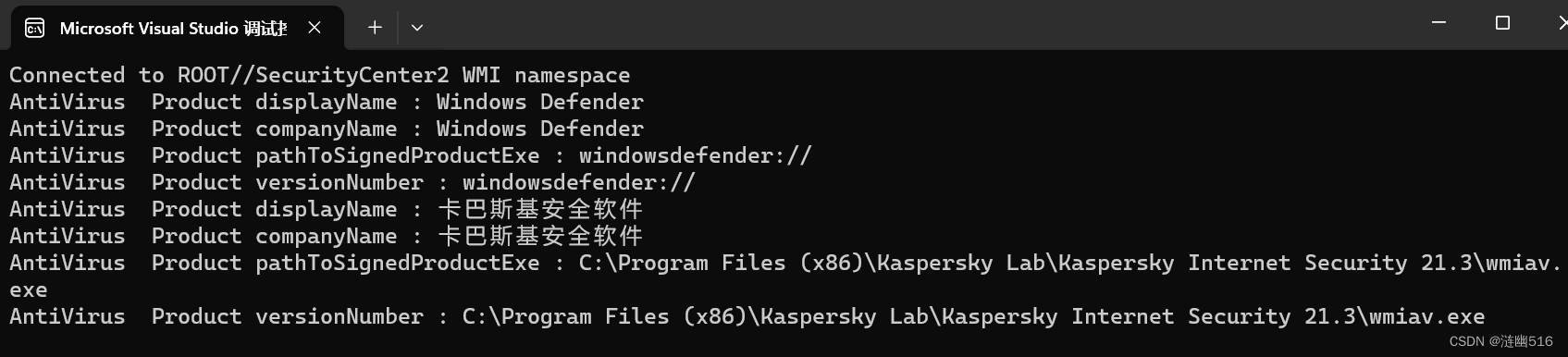
使用 WMI 查询安全软件信息
在这篇文章中,我们将详细介绍如何使用 Windows Management Instrumentation (WMI) API 来查询当前计算机上安装的安全软件的基本信息。我们将分析代码的各个部分,并解释每个步骤所涉及的技术和原理。 一、什么是 WMI? WMI 是 Windows Manag…...
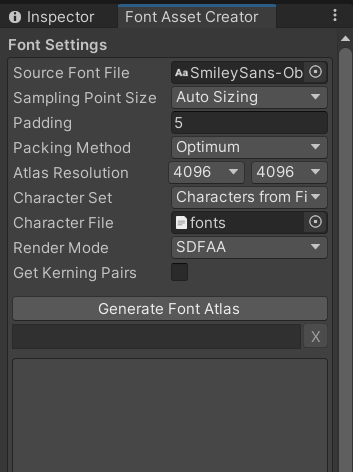
创建TextMeshPro字体文件
相比于Unity的Text组件,TextMesh Pro提供了更强大的文本格式和布局控制,更高级的文本渲染技术,更灵活的文本样式和纹理支持,更好的性能以及更易于使用的优点。但unity自带TextMeshPro字体不支持中文。这里使用普通字体文件生成Tex…...

信创ARM架构QT应用开发环境搭建
Linux ARM架构QT应用开发环境搭建 前言交叉工具链Ubuntu上安装 32 位 ARM 交叉工具链Ubuntu上安装 64 位 ARM 交叉工具链 交叉编译 QT 库下载 QT 源码交叉编译 QT 源码 Qt Creator交叉编译配置配置 Qt Creator Kits创建一个测试项目 小结 前言 有没有碰到过这种情况࿱…...
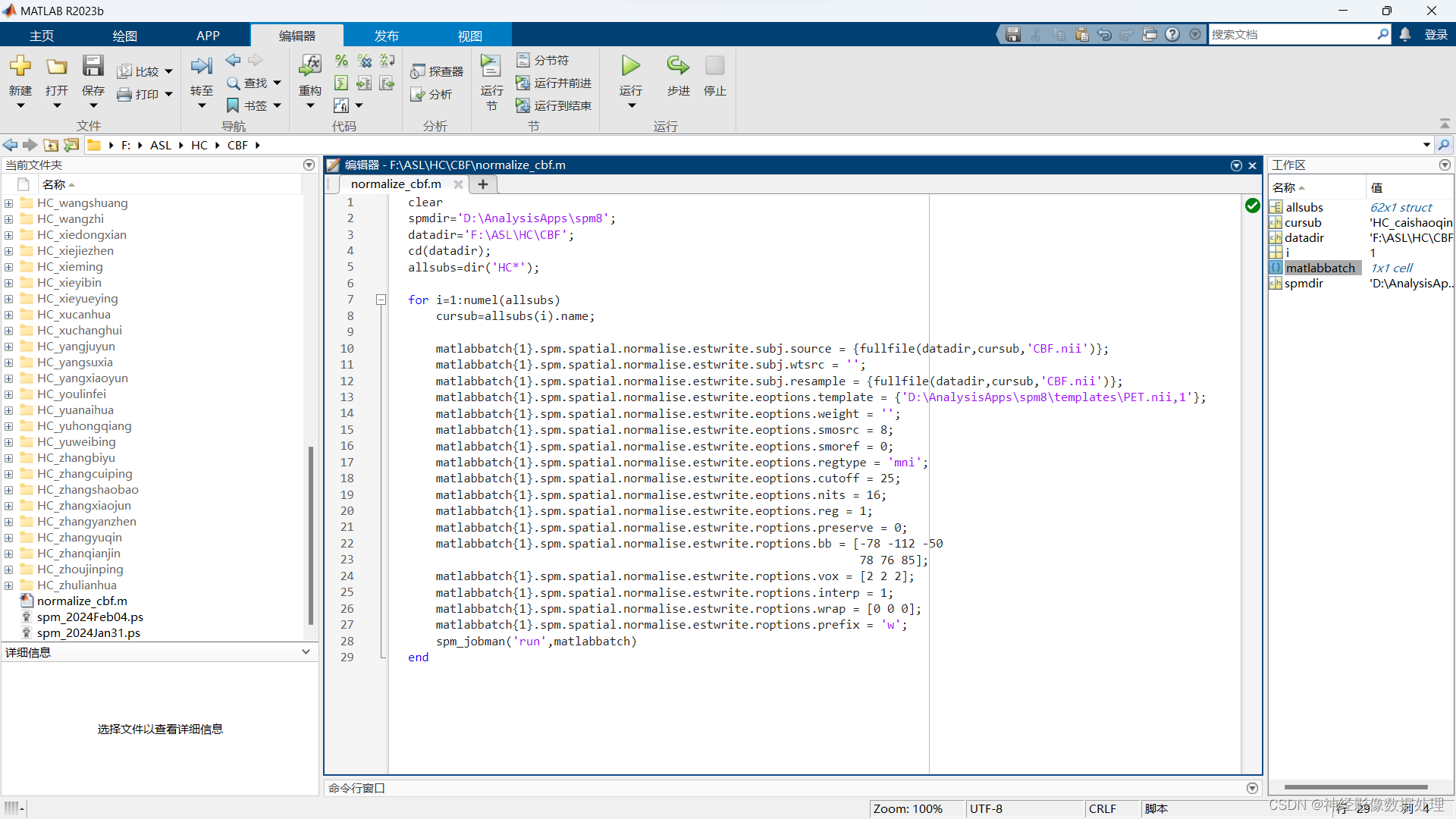
使用SPM_batch进行批量跑脚本(matlab.m)
软件:spm8matlab2023bwin11 数据格式: F:\ASL\HC\CBF\HC_caishaoqing\CBF.nii F:\ASL\HC\CBF\HC_caishaoqing\T1.nii F:\ASL\HC\CBF\HC_wangdonga\CBF.nii F:\ASL\HC\CBF\HC_wangdonga\T1.nii clear spmdirD:\AnalysisApps\spm8; datadirF:\ASL\HC\CBF…...

力扣0124——二叉树的最大路径和
二叉树的最大路径和 难度:困难 题目描述 二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。 路径和 是路径中各节点…...

c# 字符串帮助类
public class StringHelper { #region 全角半角互相转换 /// <summary> /// 转全角的函数(SBC case) /// </summary> /// <param name"str">任意字符串</param> /// <returns>全…...
LabVIEW双光子荧光显微成像系统开发
双光子显微成像是一种高级荧光显微技术,广泛用于生物学和医学研究,尤其是用于活体组织的深层成像。在双光子成像过程中,振镜(Galvo镜)扮演了非常关键的角色,它负责精确控制激光束在样本上的扫描路径。以下是…...

Prim模板
通过代码探索Prim算法:最小生成树之旅 在计算机科学领域,图算法占据了至关重要的位置,尤其是在设计高效的网络(无论是社交网络、计算机网络还是交通网)时。在这些算法中,寻找最小生成树(MST&am…...

CSS之盒子模型
盒子模型 01-选择器 结构伪类选择器 基本使用 作用:根据元素的结构关系查找元素。 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IE…...
Linux系统安装(CentOS Vmware)
学习环境安装 VMware安装 VMware下载&安装 访问官网:https://www.vmware.com 在此处可以选择语言 点击China(简体中文) 点击产品,点击Workstation Pro 下滑,点击下载试用版 下滑找到Workstation 17 Pro for Wi…...

STM32 硬件随机数发生器(RNG)
STM32 硬件随机数发生器 文章目录 STM32 硬件随机数发生器前言第1章 随机数发生器简介1.1 RNG主要特性1.2.RNG应用 第2章 RNG原理框图第3章 RNG相关寄存器3.1 RNG 控制寄存器 (RNG_CR)3.2 RNG 状态寄存器 (RNG_SR)3.3 RNG 数据寄存器 (RNG_DR) 第3章 RNG代码部分第4章 STM32F1 …...
Window环境下使用go编译grpc最新教程
网上的grpc教程都或多或少有些老或者有些问题,导致最后执行生成文件时会报很多错。这里给出个人实践出可执行的编译命令与碰到的报错与解决方法。(ps:本文代码按照煎鱼的教程编写:4.2 gRPC Client and Server - 跟煎鱼学 Go (gitbook.io)&…...
简单介绍、分类、读写流程及注意事项)
STM32——FLASH(1)简单介绍、分类、读写流程及注意事项
文章目录 FLASH的特点Nor flash和nand flashflash的读写flash 的存储单位 flash的读写过程 FLASH的特点 可擦写数据可修改可重写访问速度<ROM Nor flash和nand flash Nor flash 1、与SDRAM相似,用户可以直接运行装载到NORFLASH里面的代码,减少SRAM…...

MySQL的DML语言
DML:Data Manipulation Language(数据操作语言) DML语言用来对数据库中表的数据记录进行增、删、改操作。 一、添加数据命令 注意: 插入数据时,指定的字段顺序需要与值的顺序是一一对应的。 字符串和日期型数据应该包…...
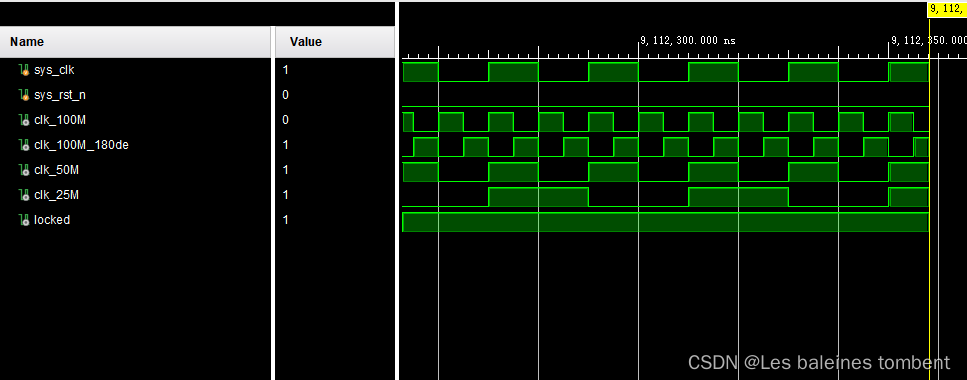
Vivado-IP核
Vivado-IP核 主程序 timescale 1ns / 1ps ////module ip_clk_wiz(input sys_clk,input sys_rst_n,output clk_out1,output clk_out2,output clk_out3,output clk_out4,output locked);clk_wiz_0 instance_name(// Clock out ports.clk_out1(clk_out1), // output clk_out…...
品牌如何营造生活感氛围?媒介盒子分享
「生活感」简而言之是指人们对生活的感受和意义,它往往没有充斥在各种重要的场合和事件中,而是更隐藏在细碎平凡的生活场景中。在营销越来越同质化的当下,品牌应该如何打破常规模式,洞察消费情绪,找到更能打动消费者心…...

Java 学习和实践笔记(2)
今天的学习进度: 注册并下载安装好了Java 8,之后进行以下配置。 1)path 是一个常见的环境变量,它告诉系统除了在当前的目标下妹寻找此程序外,还可以到path指定的目录下找。这句话是什么意思呢?以下举报例…...

Python:批量url链接保存为PDF
我的数据是先把url链接获取到存入excel中,后续对excel做的处理,各位也可以直接在程序中做处理,下面就是针对excel中的链接做批量处理 excel内容格式如下(涉及具体数据做了隐藏) 标题文件链接文件日期网页标题1http://…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
