图形学:Transform矩阵(3维 2维) 平移,旋转,缩放
0. 简介
在图形学领域中,Transform矩阵(变换矩阵)是一种表示图形对象在二维或三维空间中的位置、方向和大小变化的数学工具。它们用于执行各种图形变换,如平移、旋转、缩放。Transform矩阵通常表示为一个二维或三维矩阵,具体形式取决于空间的维度。
0.1 二维变换矩阵
- 在二维图形学中,通常使用
3x3的矩阵表示变换,其中最后一行通常是[0, 0, 1],因为二维变换不影响z轴。这个矩阵可以表示平移、旋转、缩放和剪切。 - 例如,一个简单的二维平移矩阵可以写成:
[ 1 0 tx ][ 0 1 ty ][ 0 0 1 ]
其中tx和ty是平移的水平和垂直距离。
0.2 三维变换矩阵
- 在三维图形学中,通常使用
4x4的矩阵表示变换,其中最后一列通常是[0, 0, 0, 1]。这种矩阵可以表示平移、旋转、缩放以及更复杂的变换。 - 一个简单的三维平移矩阵可以写成:
[ 1 0 0 tx ][ 0 1 0 ty ][ 0 0 1 tz ][ 0 0 0 1 ]
其中tx、ty和tz是平移的x、y和z轴距离。
不管是二维变换矩阵还是三维变换矩阵,它的最后一行都是齐次坐标,通常是[0, ... , 1]用于处理齐次坐标,使得可以用矩阵乘法来同时处理旋转和平移。
1. 举个例子
1.1 平移
给定的初始 Transform 矩阵如下:
[ 1 0 0 tx ]
[ 0 1 0 ty ]
[ 0 0 1 tz ]
[ 0 0 0 1 ]
希望在 x 轴增加 2 个单位,y 轴增加 1 个单位,z 轴减小 3 个单位。
1.1.1 计算过程
- 对 x 轴进行增加 2 个单位: 可以将 tx(原始平移量)增加 2 个单位。
- 对 y 轴进行增加 1 个单位: 将 ty(原始平移量)增加 1 个单位。
- 对 z 轴进行减小 3 个单位: 要使物体沿 z 轴负方向移动,需要将 tz 减小 3 个单位。
1.1.2 计算结果
[ 1 0 0 tx + 2 ]
[ 0 1 0 ty + 1 ]
[ 0 0 1 tz - 3 ]
[ 0 0 0 1 ]
这个新的矩阵表示了对原始物体进行了所需的平移操作。
1.2 旋转
1.2.1 2维旋转矩阵
```css
[ cos(θ) -sin(θ) ]
[ sin(θ) cos(θ) ]
1.2.1 3维旋转矩阵
- 绕x轴旋转矩阵
[ 1 0 0 0 ]
[ 0 cos(θ) -sin(θ) 0 ]
[ 0 sin(θ) cos(θ) 0 ]
[ 0 0 0 1 ]
- z轴旋转
[ cos(θ) -sin(θ) 0 0 ]
[ sin(θ) cos(θ) 0 0 ]
[ 0 0 1 0 ]
[ 0 0 0 1 ]
- 绕y轴旋转
[ cos(θ) 0 sin(θ) 0 ]
[ 0 1 0 0 ]
[-sin(θ) 0 cos(θ) 0 ]
[ 0 0 0 1 ]
原始的Transform矩阵T与旋转矩阵R相乘,得到新的Transform矩阵 T'
T' = T * R
1.3 缩放
1.3.1 缩放矩阵
[ sx 0 0 0 ]
[ 0 sy 0 0 ]
[ 0 0 sz 0 ]
[ 0 0 0 1 ]
原始的Transform矩阵T与缩放矩阵S相乘,得到新的Transform矩阵 T'
T' = T * S
相关文章:
 平移,旋转,缩放)
图形学:Transform矩阵(3维 2维) 平移,旋转,缩放
0. 简介 在图形学领域中,Transform矩阵(变换矩阵)是一种表示图形对象在二维或三维空间中的位置、方向和大小变化的数学工具。它们用于执行各种图形变换,如平移、旋转、缩放。Transform矩阵通常表示为一个二维或三维矩阵ÿ…...

Docker学习历程
Docker学习历程 Q1、docker还没启动Q2、Docker容器名称冲突的问题Q3:启动minio时发现,容器已经再重启Q4:容器被占用的情况Q5:查看日志 Q1、docker还没启动 docker run --env MODEstandalone --name nacos --restartalways -d -p …...

Android:Volley框架使用
3.15 Volley框架使用 Volley框架主要作为网络请求,图片加载工具。当应用数据量小、网络请求频繁,可以使用Volley框架。 框架Github地址:https://github.com/google/volley Volley框架的简单使用,创建项目Pro_VolleyDemo。将Github上下载Volley框架源代码,volley-master.zi…...
)
前端修炼手册(uniapp的api篇)
一、页面相关API uni.navigateTo 该API用于跳转到应用内的某个页面,可以传递参数。 uni.navigateTo({url: /pages/detail/detail?id1 })uni.redirectTo 该API用于关闭当前页面并跳转到应用内的某个页面,可以传递参数。 uni.redirectTo({url: /pages/…...

JAVA面试题16
什么是Java中的反射机制?它的用途是什么? 答案:Java的反射机制是指在运行时,通过获取类的信息来操作类的属性、方法和构造函数等。它可以用来创建对象、调用方法,以及实现动态代理等功能。 什么是Java中的泛型&#x…...

P1044 [NOIP2003 普及组] 栈题解
题目 有一个单端封闭的管子,将N(1<N<18)个不同的小球按顺序放入管子的一端。在将小球放入管子的过程中也可以将管子最顶上的一个或者多个小球倒出来。请问:倒出来的方法总数有多少种? 输入输出格式 输入格式 输入文件只含一个整数n…...
)
【DSP】数字信号处理发展里程碑(AI【文心一言】 辅助生成)
在远离尘嚣的学术殿堂中,数字信号处理(DSP)这一学科犹如一颗璀璨的明珠,其发展历程充满了传奇色彩。下面,就让我们一起穿越时空,回到那些激动人心的时刻,见证数字信号处理从无到有、从弱到强的壮…...

【JavaScript 】finally() 方法和Filter() 方法
JavaScript 中的finally() 方法 finally是 JavaScript 构造中使用的方法try-catch。try它在and阻塞之后执行catch,无论 Promise 是已履行还是已拒绝。该函数的主要作用是执行必要的清理任务并向用户传达消息。一个常见的用例可能是通知用户“您的请求已被处理”&am…...

假期作业8
线程和进程服务器 线程 #include <myhead.h>#define SIP "192.168.0.114" #define SPORT 8888void *task(void *arg){printf("客户端连接\n");sleep(1);pthread_exit(NULL); }int main(int argc, const char *argv[]) {int sfd socket(AF_INET, S…...
基于vue+node.js的校园跳蚤市场系统多商家
校园跳蚤市场系统可以在短时间内完成大量的数据处理、帮助用户快速的查找校园跳蚤市场相关信息,实现的效益更加直观。校园跳蚤市场系统中采用nodejs技术和mysql数据库。主要包括管理员、发布者和用户三大部分,主要功能是实现对个人中心、用户管理、发布者…...

Linux操作系统基础(六):Linux常见命令(一)
文章目录 Linux常见命令 一、命令结构 二、ls命令 三、cd命令 四、mkdir命令 五、touch命令 六、rm命令 七、cp命令 八、mv命令 九、cat命令 十、more命令 Linux常见命令 一、命令结构 command [-options] [parameter]说明: command : 命令名, 相应功能的英文单词…...

【Android-Compose】Material3 新版下拉刷新 PullRefresh
这里写自定义目录标题 1、(新)用于 Jetpack Compose 的刷新指示器1.1 SwipeRefresh 迁移到新的 PullRefresh1.2 迁移步骤1.3 自定义指示器 2、原始文档(SwipeRefresh )的使用依赖导入2.1 使用方法2.2 完整示例(包括视图…...
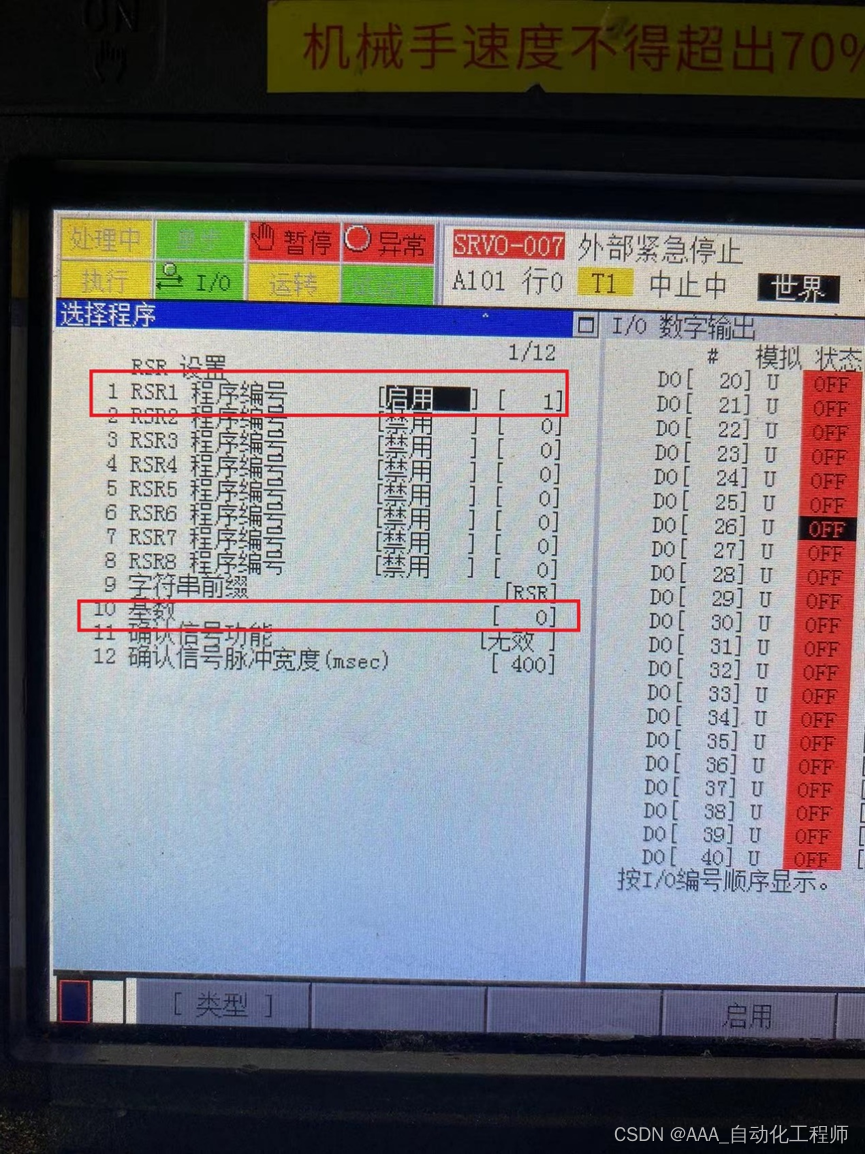
FANUC机器人外部远程启动的相关参数设置示例
FANUC机器人外部远程启动的相关参数设置示例 如下图所示,在MENU---设置---选择程序中,设置程序选择模式:RSR(这个根据自己实际使用的自动启动方式来决定,你用RSR选RSR,用PNS就选PNS), 自动运行开始方法:选择UOP,即RSR1-RSR8的启动信号分别对应UI9-UI16, 最后,点击…...

供货商、品牌方、供应链如何对接快团团头部大团长?这三个关键点你一定要记住
供货商、品牌方、供应链如何对接快团团头部大团长?这三个关键点你一定要记住 有很多的品牌方、供应链、工厂在线上拿到了不少的社群快团团团长的资源,但是真正对接上的寥寥无几,哪怕自己的品做得非常好,但是都在这个行业触了霉头…...
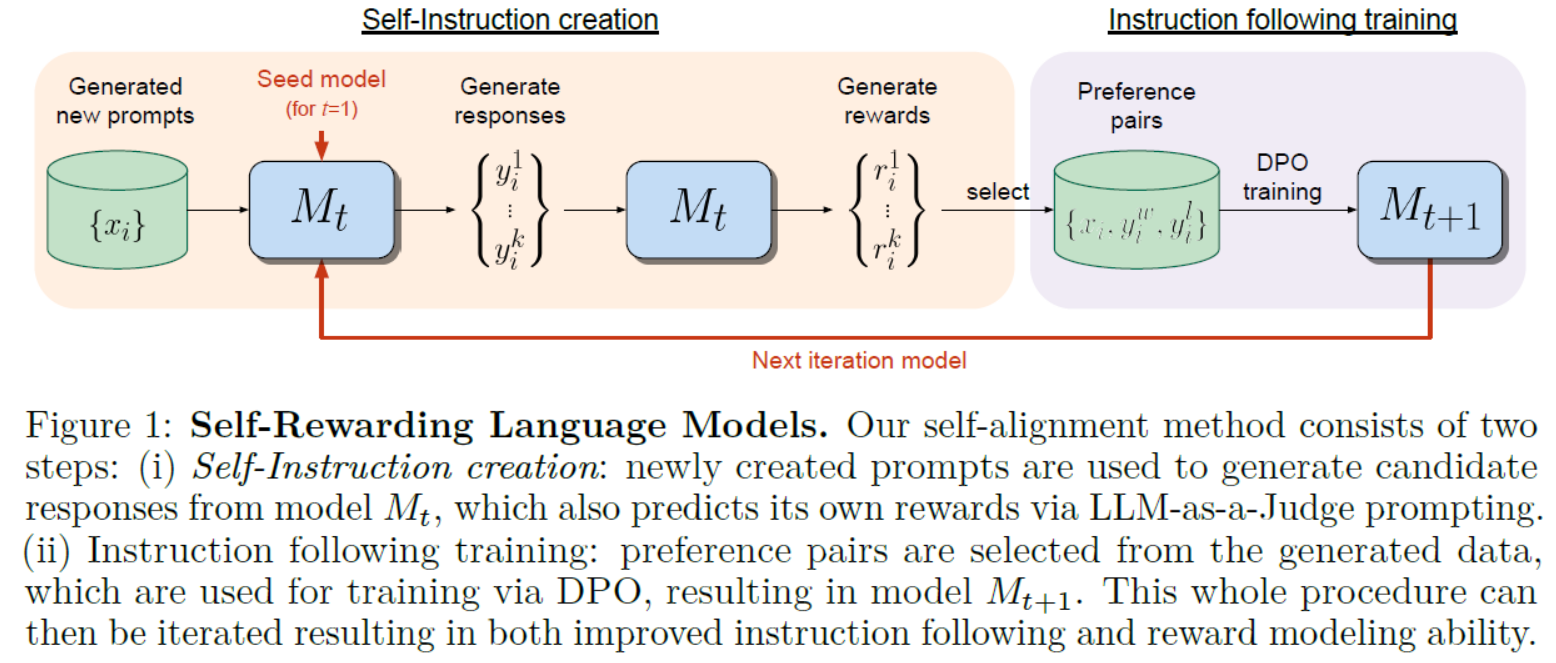
LLMs之Llama2 70B:《Self-Rewarding Language Models自我奖励语言模型》翻译与解读
LLMs之Llama2 70B:《Self-Rewarding Language Models自我奖励语言模型》翻译与解读 目录 《Self-Rewarding Language Models》翻译与解读 Abstract 5 Conclusion结论 6 Limitations限制 《Self-Rewarding Language Models》翻译与解读 地址 文章地址࿱…...

电商小程序06用户审核
目录 1 创建自定义应用2 显示待办数量3 创建审核页面4 开发审核功能5 搭建布局6 最终效果总结 上一篇我们讲解了用户注册的功能,用户注册之后状态是待审核,需要管理员进行审核。通常给管理员提供一套PC端的软件进行相关的操作,在低代码中&…...
通信:事件总线【Event Bus】)
vue3跨组件(多组件)通信:事件总线【Event Bus】
★推荐方案:使用 events npm库; 可用范围:vue、react、angular等任何框架都可使用;且使用方式完全一致; 本文仅介绍、讲解对web页面端项目的常用API;通过events实现事件总线功能; event库概述&a…...
教材管理系统
文章目录 教材管理系统一、系统演示二、项目介绍三、系统部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 教材管理系统 一、系统演示 教材管理系统 二、项目介绍 语言:nodejs 框架:egg.js、Vue 数据库…...
PV、UV、IP
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1. PV1.1 PV 计算1.2 PV 的影响因素 2. UV2.1 UV 计算2.2UV 的影响因素 3. IP3.1 IP和UV①UV大于IP②UV小于IP 三者的关系PV 和 UV 前言 PV、UV、IP是我们在运…...
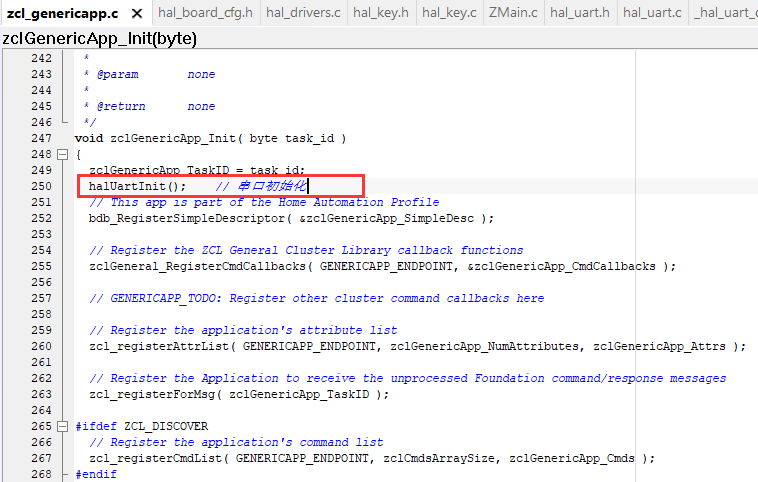
ZigBee学习——在官方例程上实现串口通信
Z-Stack版本为3.0.2 IAR版本为10.10.1 文章目录 一、添加头文件二、定义接收缓冲区三、编写Uart初始化函数四、编写串口回调函数五、函数声明六、函数调用七、可能遇到的问题(function “halUartInit“ has no prototype) 以下所有操作都是在APP层进行,也就是这个文…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
