一、西瓜书——绪论
第一章 绪论
1.独立同分布
2.假设空间
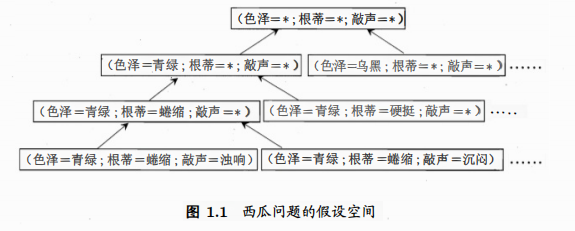
3.归纳偏好
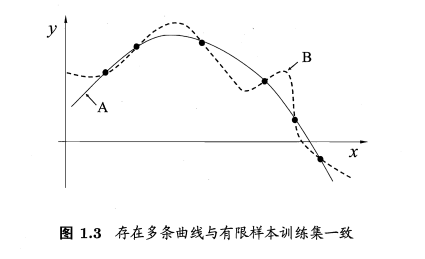
4.NFL定理
公式推导:




这个公式说明,在所有假设的情况下,误差与算法无关。所以,NFL定理最重要的寓意,是让我们清楚地认识到,脱离具体问题,空泛地谈论“什么学习算法更好”毫无意义,因为若考虑所有潜在的问题,则所有学习算法都一样好.要谈论算法的相对优劣,必须要针对具体的学习问题;在某些问题上表现好的学习算法,在另一些问题上却可能不尽如人意,学习算法自身的归纳偏好与问题是否相配,往往会起到决定性的作用.
第二章 模型评估与选择
1.训练集与测试集的划分
(1)留出法
(2)交叉验证法
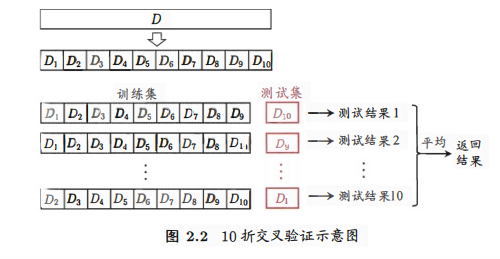
(3)自助法

自助法在数据集较小、难以有效划分训练/测试集时很有用
2.模型估计与选择
3.性能度量
(1)错误率与准确度
(2)查准率、查全率与F1

PR曲线
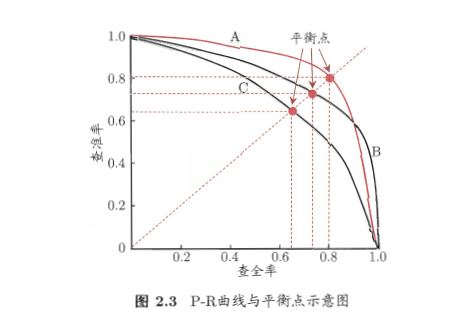
F1度量(调和均值)
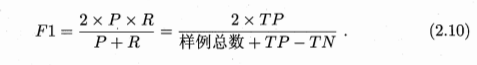
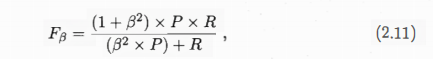

还可先将各混淆矩阵的对应元素进行平均:
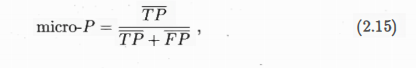

(3)ROC与AUC

AUC可通过对ROC曲线下各部分的面积求和而得.


4.代价敏感错误率与代价曲线
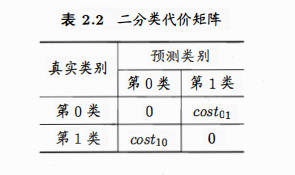
则“代价敏感”(cost-sensitive)错误率为:
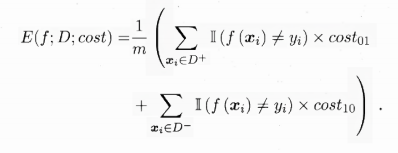
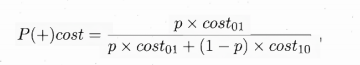
其中p是样例为正例的概率;纵轴是取值为[0,1]的归一化代价
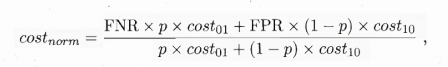
其中FPR是式(2.19)定义的假正例率,FNR=1-TPR是假反例率.代价曲线的绘制很简单:ROC曲线上每一点对应了代价平面上的一条线段,设ROC曲线上点的坐标为(TPR,FPR),则可相应计算出FNR,然后在代价平面上绘制一条从(0,FPR)到(1,FNR)的线段,线段下的面积即表示了该条件下的期望总体代价;如此将ROC曲线上的每个点转化为代价平面上的一条线段,然后取所有线段的下界,围成的面积即为在所有条件下学习器的期望总体代价,如图2.5所示.
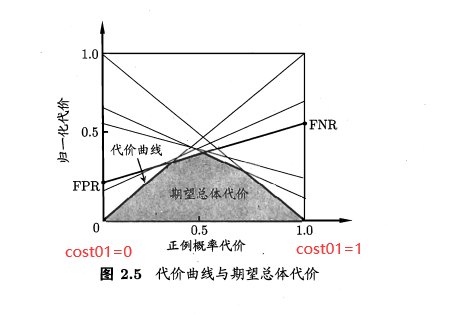
4.比较检验
机器学习中性能比较这件事要比大家想象的复杂得多.这里面涉及几个重要因素:首先,我们希望比较的是泛化性能,然而通过实验评估方法我们获得的是测试集上的性能,两者的对比结果可能未必相同;第二,测试集上的性能与测试集本身的选择有很大关系,且不论使用不同大小的测试集会得到不同的结果,即便用相同大小的测试集,若包含的测试样例不同,测试结果也会有不同;第三,很多机器学习算法本身有一定的随机性,即便用相同的参数设置在同一个测试集上多次运行,其结果也会有不同.
统计假设检验(hypothesis test)为我们进行学习器性能比较提供了重要依据.
(1)假设检验



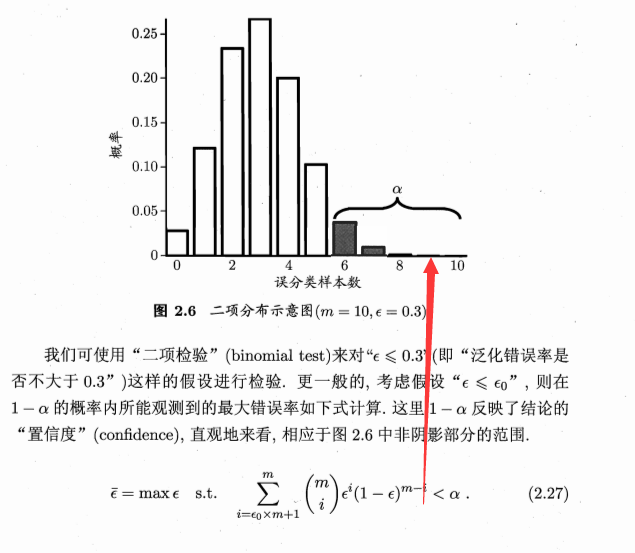

接下来查表,若t>临界值,落入拒绝域内,则拒绝原假设,否则接受原假设。认为测试错误率与泛化错误率相等。
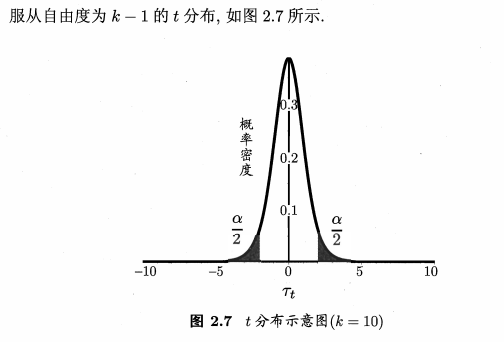
(2)交叉验证t检验
交叉验证t检验是使用的配对样本的t检验,假设学习器A,B测试错误率相等。

(3)McNemar检验

(4)Friedman检验 与 Nemenyi后续检验
McNemar检验:



五.偏差与方差
首先,引入学习算法的期望预测:
![]()


偏差(2.40)度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力;
方差(2.38)度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响;
噪声(2.39)则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度.
偏差-方差分解说明,泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的.给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小.
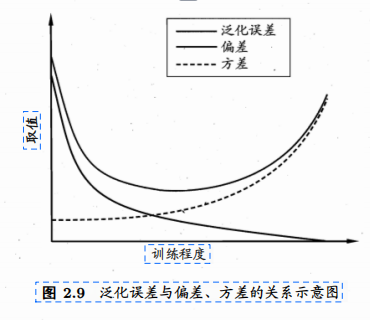
一般来说,偏差与方差是有冲突的,这称为偏差-方差窘境(bias-variancedilemma).图2.9给出了一个示意图.给定学习任务,假定我们能控制学习算法的训练程度,则在训练不足时,学习器的拟合能力不够强,训练数据的扰动不足以使学习器产生显著变化,此时偏差主导了泛化错误率;随着训练程度的加深,学习器的拟合能力逐渐增强,训练数据发生的扰动渐渐能被学习器学到,方差逐渐主导了泛化错误率;在训练程度充足后,学习器的拟合能力已非常强,训练数据发生的轻微扰动都会导致学习器发生显著变化,若训练数据自身的、非全局的特性被学习器学到了,则将发生过拟合.
相关文章:

一、西瓜书——绪论
第一章 绪论 1.独立同分布 通常 假设 样本空间 中 全 体样 本 服 从 一 个 未 知 “ 分 布 ” ( d i s t r i b u t i o n ) D , 我们获得的每个样本都是独立地从这个分布上采样获得的, 即 “ 独 立同 分布 ” ( i n d e p e n d e n t a n d i d e n t ic a …...
如何连接ChatGPT?无需科学上网,使用官方GPT教程
随着AI的发展,ChatGPT也越来越强大了。 它可以帮你做你能想到的几乎任何事情,妥妥的生产力工具。 然而,对于许多国内的用户来说,并不能直接使用ChatGPT,不过没关系,我最近发现了一个可以直接免科学上网连…...
qt学习:串口
头文件 #include <QSerialPort> #include <QSerialPortInfo> 模块 QT core gui serialport 编程步骤 配置一个ui界面,五个QComboBox和一个按钮和一个QTextEdit 添加一个成员 private:QSerialPort *serial; 在构造函数中初始化ui端口列表和…...
145. 二叉树的后序遍历
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。 示例 1: 输入:root [1,null,2,3] 输出:[3,2,1]示例 2: 输入:root [] 输出:[]示例 3: 输入:root [1] 输…...
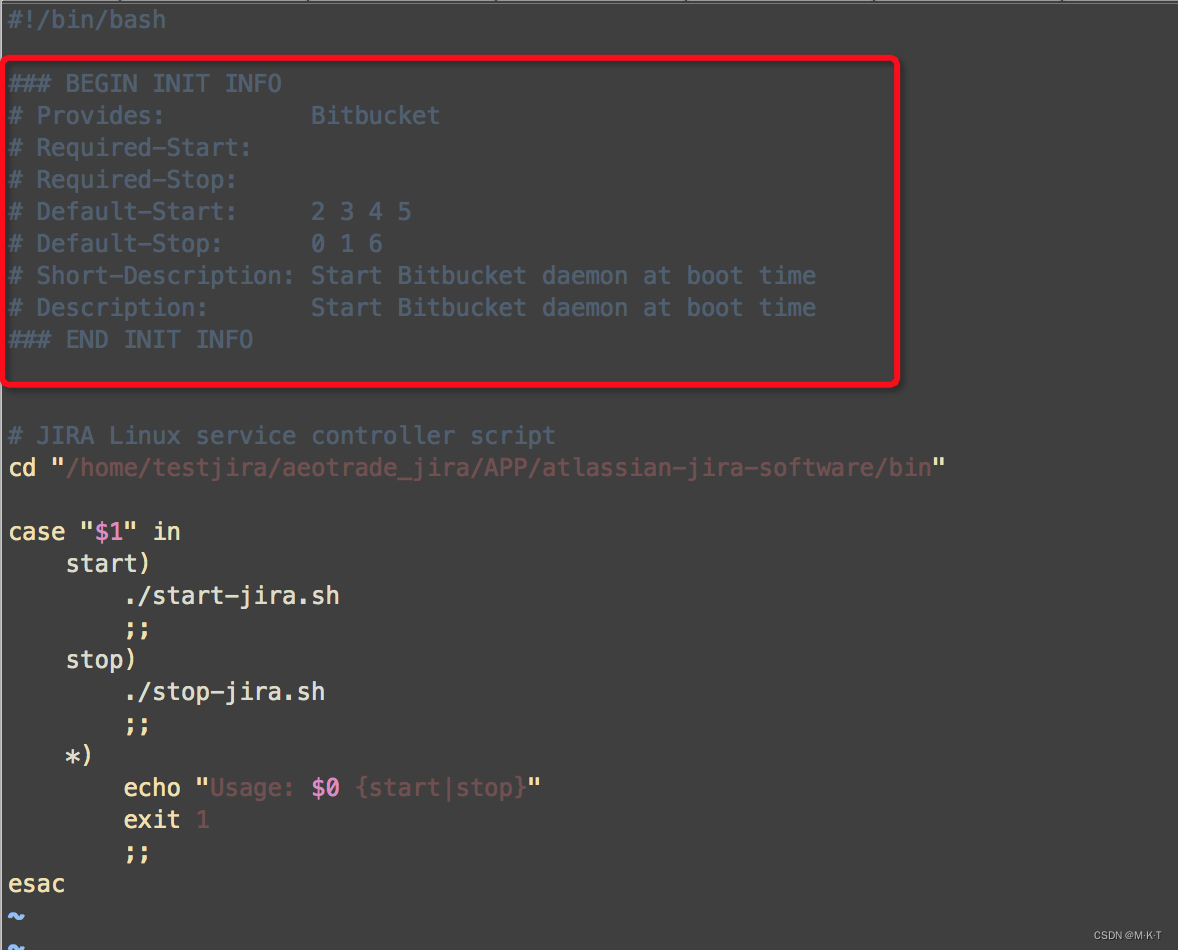
Postgresql 的编译安装与包管理安装, 全发行版 Linux 通用
博客原文 文章目录 实验环境信息编译安装获取安装包环境依赖编译安装安装 contrib 下工具代码 创建用户创建数据目录设置开机自启动启动数据库常用运维操作 apt 安装更新源安装 postgresql开机自启修改配置修改密码 实验环境信息 Ubuntu 20.04Postgre 16.1 编译安装 获取安装…...
【Java EE初阶十】多线程进阶二(CAS等)
1. 关于CAS CAS: 全称Compare and swap,字面意思:”比较并交换“,且比较交换的是寄存器和内存; 一个 CAS 涉及到以下操作: 下面通过语法来进一步进项说明: 下面有一个内存M,和两个寄存器A,B; CAS(M,A,B)&am…...

与AI对话:编写高效Prompt的指南
与AI对话:编写高效Prompt的指南 一、明确目标 引导AI提供特定格式或内容答案的策略一、明确需求二、使用示例三、设置参数四、分步询问五、使用关键词 利用关键词引导AI重点关注核心内容的技巧一、确定关键概念二、使用专业术语三、强调重要性四、避免相关术语的混淆…...
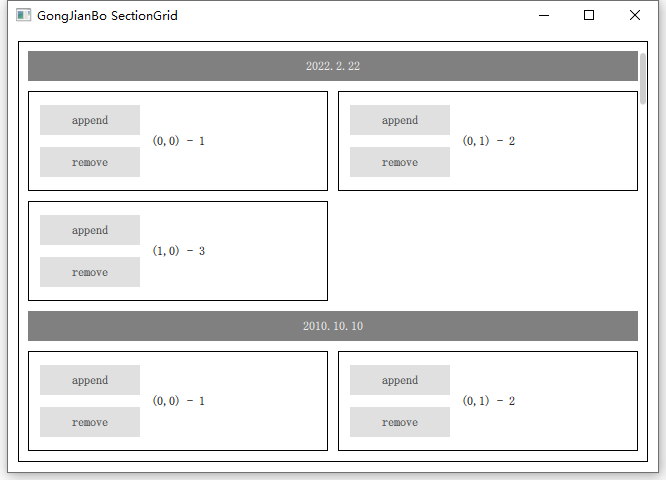
QML用ListView实现带section的GridView
QML自带的GridView只能定义delegate,没有section,类似手机相册带时间分组标签的样式就没法做。最简单的方式就是组合ListViewGridView,或者ListViewFlow,但是嵌套View时,子级View一般是完全展开的,只显示该…...

docker之程序镜像的制作
目录 一、每种资源的预安装(基础) 安装 nginx安装 redis 二、dockerfile文件制作(基础) 打包 redis 镜像 创建镜像制作空间制作dockerfile 打包 nginx 镜像 三、创建组合镜像(方式一) 生成centos容器并…...

Git - 每次 git pull/push 时需要账号和密码解决方案
问题描述 在提交项目代码或者拉取代码的时候,每次 git 都要输入用户名密码,很烦~ 解决方案 让服务器记下来用户名和密码,此时输入一次,以后再 git push /pull 的时候就不用再输账号和密码了 # 配置 git 记录用户名和密码 git c…...

C语言中在main函数之后运行的函数
在 Linux 平台上,atexit 函数同样是一个用于注册终止处理函数的库函数,它是 C 标准库 <stdlib.h> 的一部分。atexit 函数允许你注册一个或多个函数,这些函数会在 main 函数执行结束后,或者在调用 exit 函数时,由…...
pytorch训练指标记录之tensoboard,wandb
详解Tensorboard及使用教程_tensorboard怎么用-CSDN博客文章浏览阅读5.1w次,点赞109次,收藏456次。目录一、什么是Tensorboard二、配置Tensorboard环境要求安装三、Tensorboard的使用使用各种add方法记录数据单条曲线(scalar)多条曲线(scalars)直方图(hi…...

C语言——oj刷题——实现字符串逆序
当我们需要逆序一个字符串的内容时,可以通过C语言编写一个函数来实现。下面将详细介绍如何通过C语言实现这个功能,并附上代码示例。 1、实现原理 要逆序一个字符串的内容,可以使用两个指针来交换字符串中对应位置的字符。具体实现原理如下&am…...
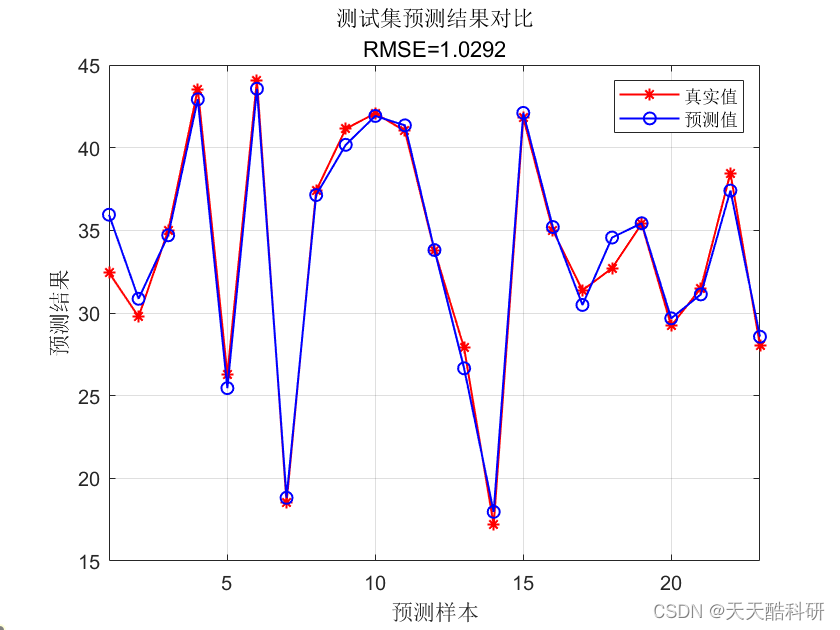
空气质量预测 | Matlab实现基于SVR支持向量机回归的空气质量预测模型
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 政府机构使用空气质量指数 (AQI) 向公众传达当前空气污染程度或预测空气污染程度。 随着 AQI 的上升,公共卫生风险也会增加。 不同国家有自己的空气质量指数,对应不同国家的空气质量标准。 基于支持向量机(Su…...

Vue中的请求拦截器
目录 1 前言 2 使用方法 2.1 创建拦截器 2.2 引入拦截器 1 前言 我们常常会使用JWT令牌来验证登录,因此很多请求都需要携带JWT令牌,我们当然可以用{headers:{Authorization:xx}}的方式,向每个请求中都以这样的方式添加JWT令牌。不过这样…...
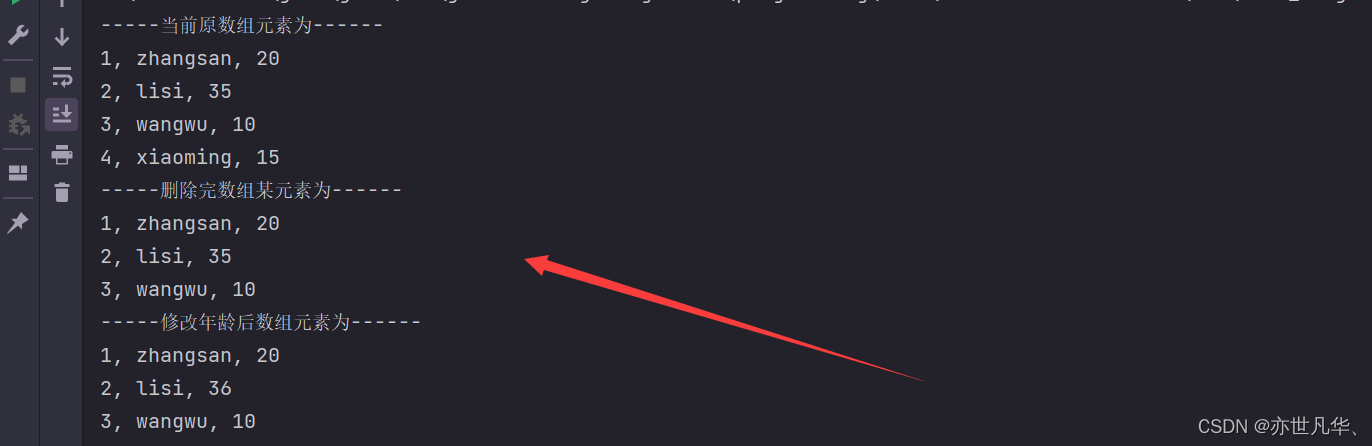
Java奠基】对象数组练习
目录 商品对象信息获取 商品对象信息输入 商品对象信息计算 商品对象信息统计 学生数据管理实现 商品对象信息获取 题目要求是这样的: 定义数组存储3个商品对象。 商品的属性:商品的id,名字,价格,库存。 创建三个…...

排序算法---快速排序
原创不易,转载请注明出处。欢迎点赞收藏~ 快速排序是一种常用的排序算法,采用分治的策略来进行排序。它的基本思想是选取一个元素作为基准(通常是数组中的第一个元素),然后将数组分割成两部分,其中一部分的…...
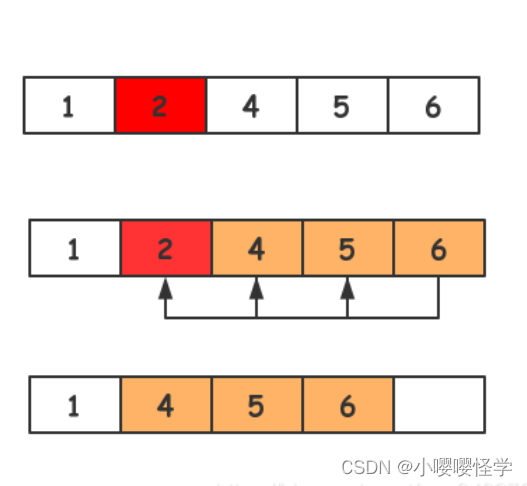
算法||实现典型数据结构的查找、添加和删除数据 并分析其时间和空间复杂度
实现典型数据结构的查找、添加和删除数据 并分析其时间和空间复杂度 线性结构: 数组:是一种线性表数据结构,它用一组连续的内存空间,来存储一组具有相同类型的数据。 查找数据 :随机访问 流程图 /** 查询元素下标…...

【蓝桥杯冲冲冲】Invasion of the Milkweed G
【蓝桥杯冲冲冲】Invasion of the Milkweed G 蓝桥杯备赛 | 洛谷做题打卡day30 文章目录 蓝桥杯备赛 | 洛谷做题打卡day30[USACO09OCT] Invasion of the Milkweed G题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 题解代码我的一些话 [USACO09OCT] Invasion of the Mi…...

【JAVA WEB】 百度热榜实现 新闻页面 Chrome 调试工具
目录 百度热榜 新闻页面 Chrome 调试工具 --查看css属性 打开调试工具的方式 标签页含义 百度热榜 实现效果: 实现代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"vi…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
