假期刷题打卡--Day26
1、MT1212乘法表
请编写一个简单程序,输出九九乘法表。输入n,就输出乘法表到n的地方。
格式
输入格式:
输入整型
输出格式:
输出整型。形式如:1*1=1
样例 1
输入:
5
输出:
1*1=1 2*1=2 2*2=4 3*1=3 3*2=6 3*3=9 4*1=4 4*2=8 4*3=12 4*4=16 5*1=5 5*2=10 5*3=15 5*4=20 5*5=25
备注
乘式之间一个空格。乘法结果占两格,不足两位的左对齐。
分析过程
本题实现的是我们从小背的九九乘法表的表示,使用的是双重循环。唯一需要注意的是,本题中对于空格的要求是不同的,要注意备注中所说的,不然就算代码是能够输出乘法表的,也无法通过所有用例。

所以,就要按照备注将空格进行修改。
按照备注可得,不足两位的占2个空格,除此之外,乘法之间占用1个空格。
实现代码
#include<bits/stdc++.h> using namespace std;int main( )
{int n;scanf("%d",&n);for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){if(i*j>=10){printf("%d*%d=%d ",i,j,i*j);}else{printf("%d*%d=%d ",i,j,i*j);}}printf("\n");}return 0;
}2、MT1213 x个a
求a+aa+aaa+…+a…a(x个a),x和a由键盘输入。
格式
输入格式:
输入为整型,空格分隔
输出格式:
输出为整型
样例 1
输入:
3 1
输出:
123
分析过程
本来想的是,使用一个循环,循环结束条件为x,然后在这个循环中,改变a的值,求出sum。按照这个代码实现的代码如下:
#include<bits/stdc++.h> using namespace std;int main( )
{int x,a,sum;cin >> x >> a;sum = a;for(int i=1;i<x;i++){// cout << a << "&" << sum << "^";a = a + pow(10,i);// cout << a <<"*";sum += a;}cout << sum;return 0;
}但是,这个代码无法通过所有的用例,只能通过一个用例

所以,继续分析遗漏点。
是因为,在测试用例的时候,a为1,所以恰巧可以通过,而如果a不为1,按照我上面写的代码,最高位始终为1,所以结果是错误的。要修改为正确答案,就需要在最高位乘以a,实现代码如下:
实现代码
#include<bits/stdc++.h> using namespace std;int main( )
{int x,a,sum,b;cin >> x >> a;sum = a,b=a;for(int i=1;i<x;i++){// cout << a << "&" << sum << "^";a = a + b*pow(10,i);
// cout << a <<"*";sum += a;}cout << sum;return 0;
}需要注意的是,a是随着i的增加而改变的,所以不能直接在高位乘以a,而是要在最初的时候,就把a保存在一个变量当中,在最高位乘以这个数即可。
3、MT1214上三角矩阵
输入3X3的整型矩阵A,输出对应的上三角矩阵。
格式
输入格式:
输入矩阵,元素在0到9之间,空格分隔。
输出格式:
输出矩阵,空格分隔。
样例 1
输入:
1 2 3 4 5 6 7 8 9
输出:
1 2 3 0 5 6 0 0 9
解决思路
法一:因为本题要求的矩阵是3*3的矩阵,是固定的,所以可以直接使用一维数组,找出上三角矩阵包含的几位,除了这几位,其余的都直接设置位0即可。
法二:使用二维数组,设置为a[i][j],当i>j时,输入0。然后输出矩阵即可。
实现代码
法一:一维矩阵解决
#include<bits/stdc++.h> using namespace std;int main( )
{int a[9]={0},count=0;for(int i=0;i<9;i++){//这里需要注意,数组位数为9位,所以应该是从0~8cin >> a[i];if(i==3||i==6||i==7){a[i]=0;}}for(int i=0;i<9;i++){// cout << a[i];count++;cout << a[i] << " ";if(count%3==0){cout << endl;}}return 0;
}法二:二维矩阵解决
#include<bits/stdc++.h> using namespace std;int main( )
{int a[3][3]={0};for(int i=0;i<3;i++){for(int j=0;j<3;j++){cin >> a[i][j];if(i>j) a[i][j]=0;}}for(int i=0;i<3;i++){for(int j=0;j<3;j++){cout << a[i][j] << " ";}cout << endl;}return 0;
}明天继续吧。
相关文章:

假期刷题打卡--Day26
1、MT1212乘法表 请编写一个简单程序,输出九九乘法表。输入n,就输出乘法表到n的地方。 格式 输入格式: 输入整型 输出格式: 输出整型。形式如:1*11 样例 1 输入: 5输出: 1*11 2*12 …...
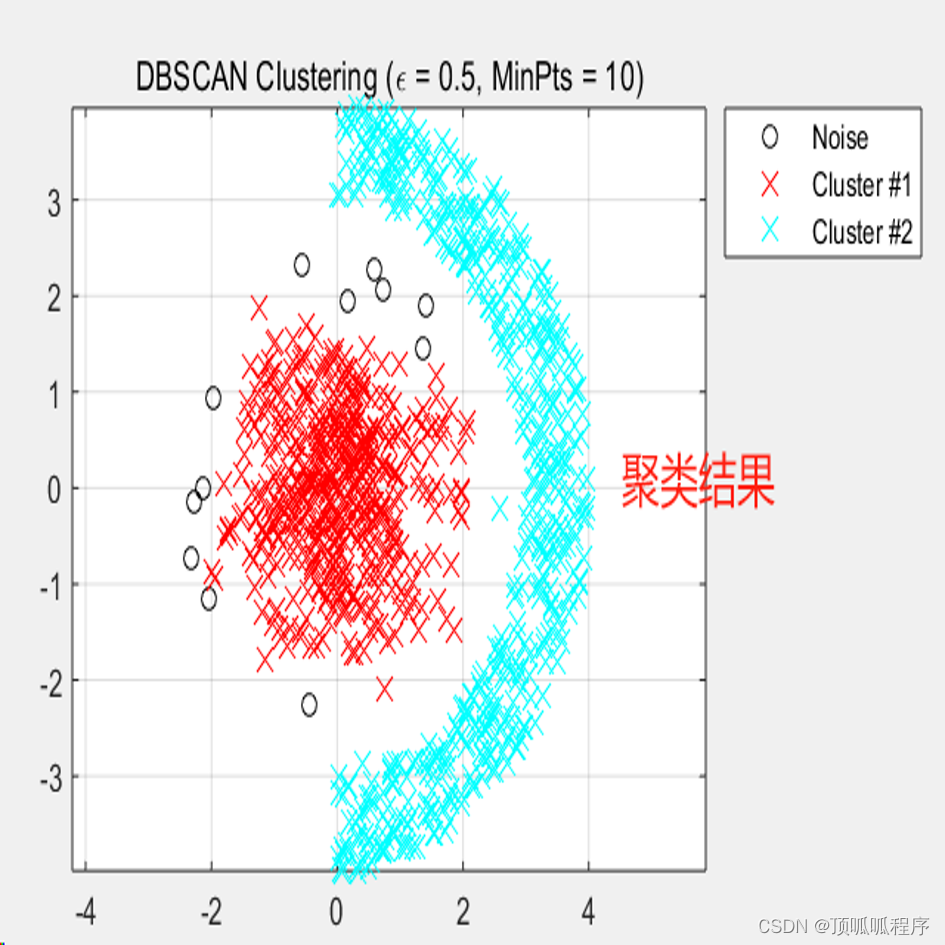
159基于matlab的基于密度的噪声应用空间聚类(DBSCAN)算法对点进行聚类
基于matlab的基于密度的噪声应用空间聚类(DBSCAN)算法对点进行聚类,聚类结果效果好,DBSCAN不要求我们指定集群的数量,避免了异常值,并且在任意形状和大小的集群中工作得非常好。它没有质心,聚类簇是通过将相邻的点连接…...

CVPR 2023: GANmouflage: 3D Object Nondetection with Texture Fields
我们使用以下6个分类标准对本文的研究选题进行分析: 1. 伪装类型: 自然伪装: 此类别关注受自然界伪装策略启发或直接复制的研究。这包括研究动物的体色、图案和纹理,为人工伪装的设计提供信息,通常以生物学真实性和有效性为目标 (例如,参考文献 [12, 19, 30, 48])。人工伪…...

【ASP.NET Core 基础知识】--部署和维护--日志记录和错误处理
一、日志记录(Logging) 1.1 日志记录的概念 日志记录是一种记录系统运行状态、活动和事件的重要机制。在软件开发和系统管理中,日志记录扮演着关键角色,用于追踪应用程序的执行过程、监视系统的健康状况、诊断问题和安全审计等。在ASP.NET Core等现代W…...

docker命令梳理
docker镜像操作 //从硬盘加入镜像 docker load -i xxx.tar //基于dockerfile构建镜像 docker build -t xxx:xxx . //查看镜像 docker images //镜像改名 docker tag //docker镜像提交到容器 //docker commit [-m“描述信息”] [-a“作者”]容器id 镜像名[:标签名] docker镜像仓…...
彩虹系统7.0免授权+精美WAP端模板源码
最低配置环境 PHP7.2 1、上传源码到网站根目录,导入数据库文件 2、修改数据库配置文件:/config.php 3、后台:/admin 账号: 4、前台用户:123456 密码:1234561...

linux系统haproxy负载均衡工具的介绍以及使用
haproxy 概述haproxy的特点haproxy算法haproxy做四层负载均衡haproxy做七层负载均衡 概述 ha-proxy是一款高性能的负载均衡软件。其专注于负载均衡这一些事情,因此与nginx比起来,负载均衡做的更好haproxy---主要是做负载均衡的7层,也可以做4…...

七、Nacos源码系列:Nacos服务发现
目录 一、服务发现 二、getServices():获取服务列表 2.1、获取服务列表 2.2、总结图 三、getInstances(serviceId):获取服务实例列表 3.1、从缓存中获取服务信息 3.2、缓存为空,执行订阅服务 3.2.1、调度更新,往线程池中…...
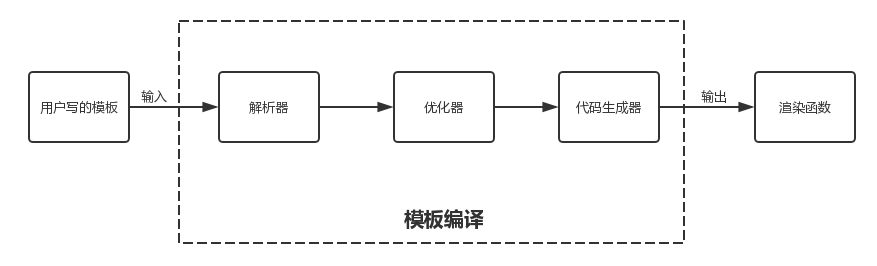
Vue源码系列讲解——模板编译篇【一】(综述)
目录 1. 前言 2. 什么是模板编译 3. 整体渲染流程 4. 模板编译内部流程 4.1 抽象语法树AST 4.2 具体流程 5. 总结 1. 前言 在前几篇文章中,我们介绍了Vue中的虚拟DOM以及虚拟DOM的patch(DOM-Diff)过程,而虚拟DOM存在的必要条件是得先有VNode&…...

【机器学习】数据清洗之识别异常点
🎈个人主页:甜美的江 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步…...

MacOS 制作 TF 卡/ U 盘镜像
最近有张老的 TF 卡没办法直接拷贝里面的数据,于是打算利用 dd 工具直接全卡拷贝为镜像再分析里面的数据 在终端中,输入以下命令来列出所有磁盘设备: diskutil list这将显示Mac上所有的磁盘设备。你需要找到TF卡对应的设备,它通…...
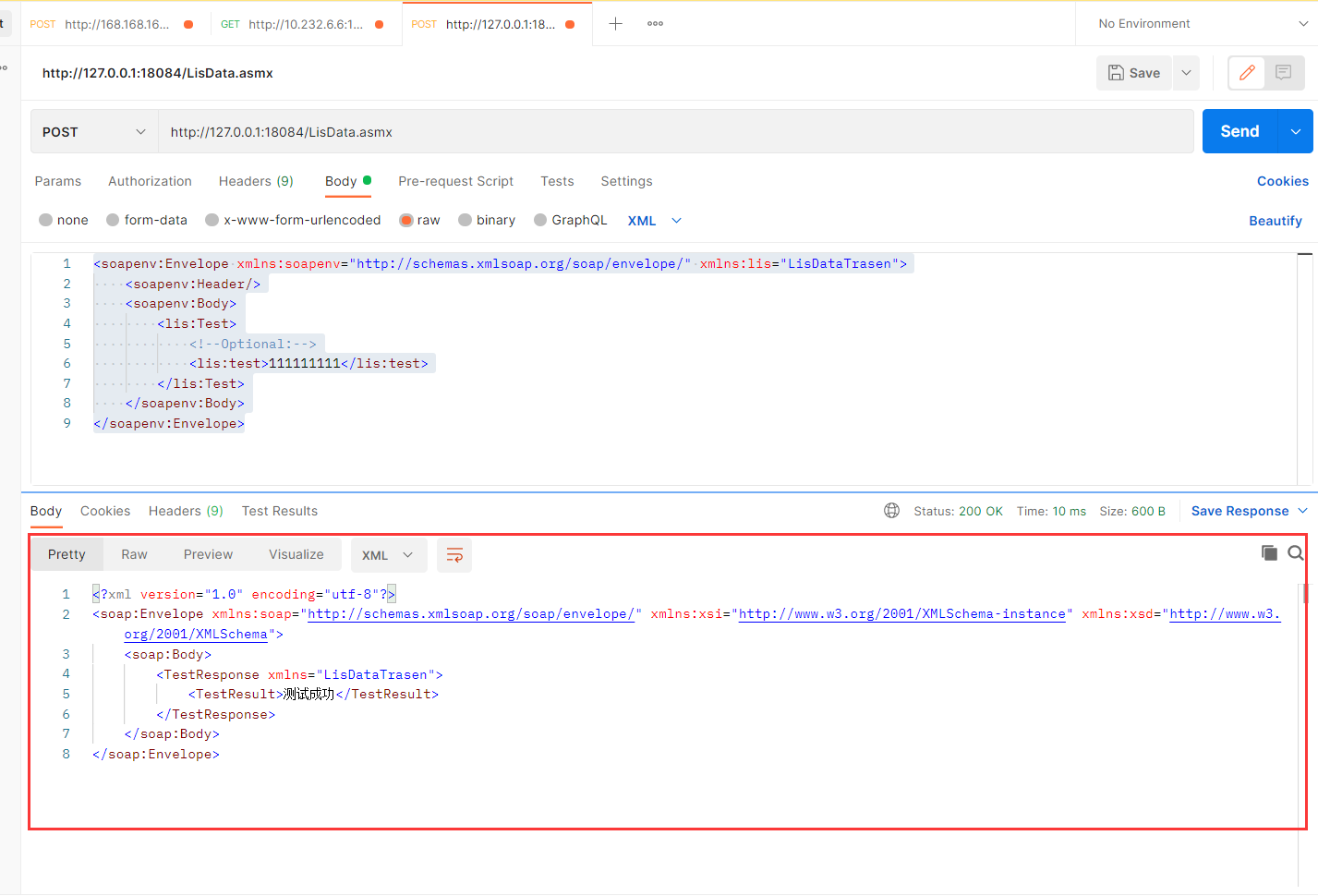
怎么用postman调用webservice(反推SoapUI)
<soapenv:Envelope xmlns:soapenv“http://schemas.xmlsoap.org/soap/envelope/” xmlns:lis“LisDataTrasen”> soapenv:Header/ soapenv:Body lis:Test lis:test111111111</lis:test> </lis:Test> </soapenv:Body> </soapenv:Envelope> Conten…...

【开源】JAVA+Vue.js实现衣物搭配系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 衣物档案模块2.2 衣物搭配模块2.3 衣物收藏模块 三、系统设计3.1 用例设计3.2 E-R图设计3.3 数据库设计3.3.1 衣物档案表3.3.2 衣物搭配表3.3.3 衣物收藏表 四、系统实现4.1 登录页4.2 衣物档案模块4.3 衣物搭配模块4.4…...

【Flask + AI】接入CHATGLM API 实现翻译接口
【Flask AI】接入CHATGLM API 实现翻译接口 最近的项目中,需要加一个翻译功能,正好chatglm4发布了,于是决定着手用它实现。 https://chatglm.cn 准备 首先,在chatglm开发者中心申请api key,这里不再赘述 其次&…...

并发事务带来的问题及解决方法
引言 在数据库系统中,事务是指一组操作被视为一个逻辑单元,要么全部执行成功,要么全部不执行,保证数据库的一致性和完整性。而并发事务则是指多个事务同时执行的情况。虽然并发事务能够提高系统的性能和吞吐量,但也会…...

CRNN介绍:用于识别图中文本的深度学习模型
CRNN:用于识别图中文本的深度学习模型 CRNN介绍:用于识别图中文本的深度学习模型CRNN的结构组成部分工作原理 CRNN结构分析卷积层(Convolutional Layers)递归层(Recurrent Layers)转录层(Transc…...

机器人运动学林沛群——变换矩阵
对于仅有移动,由上图可知: A P B P A P B o r g ^AP^BP^AP_{B org} APBPAPBorg 对于仅有转动,可得: A P B A R B P ^AP^A_BR^BP APBARBP 将转动与移动混合后,可得: 一个例子 在向量中ÿ…...
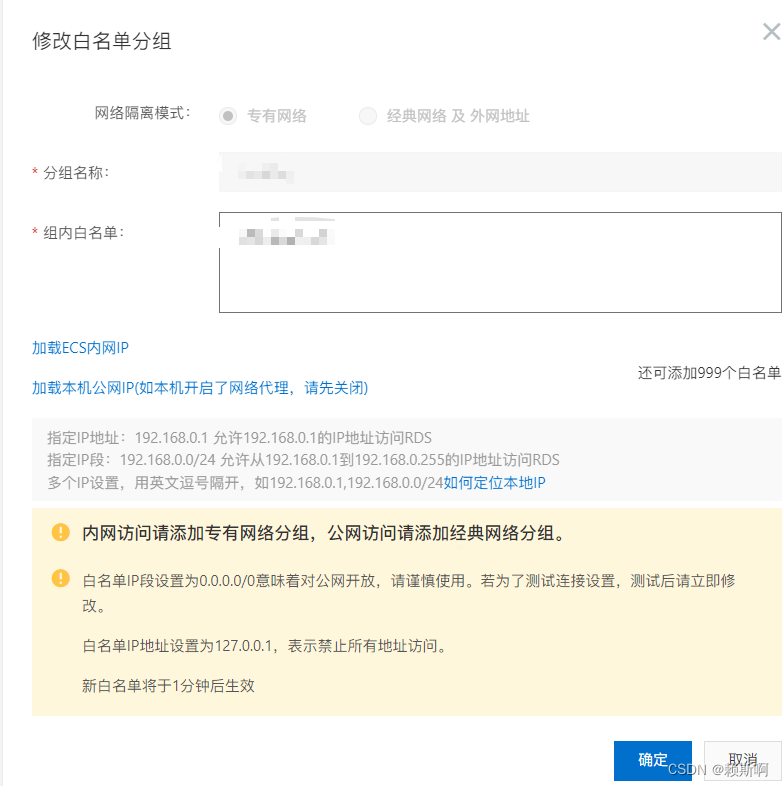
阿里云增加数据库访问白名单
阿里云增加数据库访问白名单 概况 我们希望在外网访问数据库时,可能会遇到无法连接的问题,这有可能是被拦截了。这时就需要去查看自己的ip有没有在白名单里面,没有的话就把ip加入到白名单。 路径 阿里云控制台-搜索RDS-进入RDS管理控制台…...

Rust基础拾遗--辅助功能
Rust基础拾遗 前言1.错误处理1.1 panic为什么是 Result 2. create与模块3. 宏4. 不安全代码5. 外部函数 前言 通过Rust程序设计-第二版笔记的形式对Rust相关重点知识进行汇总,读者通读此系列文章就可以轻松的把该语言基础捡起来。 1.错误处理 Rust 中的两类错误处理…...
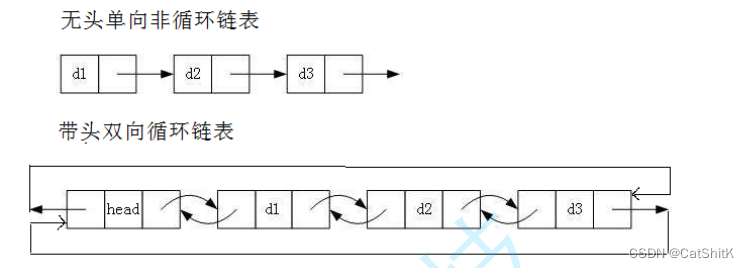
【数据结构】双向链表(链表实现+测试+原码)
前言 在双向链表之前,如果需要查看单链表来复习一下,链接在这里: http://t.csdnimg.cn/Ib5qS 1.双向链表 1.1 链表的分类 实际中链表的结构非常多样,以下情况组合起来就有8种链表结构: 1.1.1 单向或者双向 1.1.2 …...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
