三、搜索与图论
DFS
排列数字

#include<iostream>
using namespace std;
const int N = 10;
int a[N], b[N];
int n;void dfs(int u){if(u > n){for(int i = 1; i <= n; i++)cout<<a[i]<<" ";cout<<endl;return;}for(int i = 1; i <= n; i++){if(!b[i]){b[i] = 1;a[u] = i;dfs(u + 1);b[i] = 0;}}
}int main(){cin>>n;dfs(1);return 0;
}
n-皇后问题

#include<iostream>
using namespace std;
const int N = 20;
char g[N][N];
int a[N], b[N], c[N];
int n;void dfs(int u){if(u > n){for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++)cout<<g[i][j];cout<<endl;}cout<<endl;return;}for(int i = 1; i <= n; i++){if(!a[i] && !b[u + i] && !c[-u + i + n]){a[i] = b[u + i] = c[-u + i + n] = 1;g[u][i] = 'Q';dfs(u + 1);g[u][i] = '.';a[i] = b[u + i] = c[-u + i + n] = 0;}}
}int main(){cin>>n;for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)g[i][j] = '.';dfs(1);return 0;
}
BFS
走迷宫

#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
int g[N][N], d[N][N];
pair<int, int> q[N * N];
int hh, tt = - 1;
int n, m;int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};void bfs(int x, int y){memset(d, -1, sizeof(d));q[++tt] = make_pair(x, y);d[x][y] = 0;while(hh <= tt){auto t = q[hh++];for(int i = 0; i < 4; i++){int a = dx[i] + t.first, b = dy[i] + t.second;if(a < 1 || a > n || b < 1 || b > m) continue;if(d[a][b] != -1) continue;if(g[a][b] != 0) continue;d[a][b] = d[t.first][t.second] + 1;q[++tt] = make_pair(a, b);}}cout<<d[n][m];
}int main(){cin>>n>>m;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)cin>>g[i][j];bfs(1, 1);return 0;
}
八数码


#include<iostream>
#include<unordered_map>
using namespace std;
const int N = 1e6; //一共有9!种情况
unordered_map<string, int> d;
string q[N];
int hh, tt = -1;
int n = 9;int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};int bfs(string s){q[++tt] = s;d[s] = 0;//记录终点string end = "12345678x";while(hh <= tt){string t = q[hh++];//存储当前位置到起点的距离int dis = d[t];//如果到终点了,那就返回距起点距离if(t == end) return dis;//查找x的下标int k = t.find('x');//x在矩阵中的位置int x = k / 3, y = k % 3;for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a < 0 || a > 2 || b < 0 || b > 2) continue;//转移xswap(t[k], t[3 * a + b]);//如果没有遍历过,那就存储到队列中if(!d.count(t)){d[t] = dis + 1;q[++tt] = t;}//还原swap(t[k], t[3 * a + b]);}}return -1;
}int main(){char c;string s = "";for(int i = 0; i < n; i++){cin>>c;s += c;}cout<<bfs(s);return 0;
}
树和图的存储
树是一种特殊的图
存储可以用链式向前星或者vector
//链式向前星
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[N], ne[N], idx;
int st[N];void add(int a, int b){e[idx] = b;ne[idx] = h[a];h[a] = idx;idx++;
}void dfs(int u){st[u] = 1;for(int i = u; i != -1; i = ne[i]){int j = e[i];if(!st[j]) dfs(j);}
}int main(){memset(h, -1, sizeof(h));return 0;
}//vector存储
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5 + 10;
vector<int> v[N];
int st[N];void add(int a, int b){v[a].push_back(b);v[b].push_back(a);
}void dfs(int u){st[u] = 1;for(int i = 0; i < v[u].size(); i++){int j = v[u][i];if(!st[j]) dfs(j);}
}int main(){return 0;
}
树与图的深度优先遍历
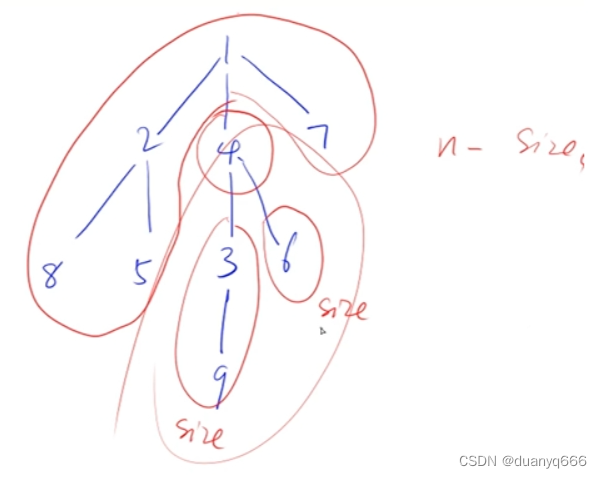
树的重心

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int st[N];
int n, ans = 1e9;void add(int a, int b){e[idx] = b;ne[idx] = h[a];h[a] = idx;idx++;
}int dfs(int u){st[u] = 1;//cnt存储以u为根的节点数(包括u),res是删除掉某个节点后的最大连通子图节点数int cnt = 1, res = 0; for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(!st[j]){//以u为节点的单棵子树的节点数int t = dfs(j);//计算以j为根的树的节点数cnt += t;//记录最大连通子图节点数res = max(res, t);}}//以u为重心,最大的连通子图节点数res = max(res, n - cnt);ans = min(ans, res);return cnt;
}int main(){memset(h, -1, sizeof(h));cin>>n;int a, b;for(int i = 0; i < n - 1; i++){cin>>a>>b;add(a, b);add(b, a);}dfs(1);cout<<ans;return 0;
}
树与图的宽度优先遍历
图中点的层次

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int q[N], d[N], hh, tt = -1;
int n, m;void add(int a, int b){e[idx] = b;ne[idx] = h[a];h[a] = idx;idx++;
}void bfs(int u){memset(d, -1, sizeof(d));q[++tt] = u;d[u] = 0;while(hh <= tt){//使用队头,弹出队头int t = q[hh++];for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(d[j] == -1){//更新距离d[j] = d[t] + 1;//入队q[++tt] = j;}}}cout<<d[n];
}int main(){memset(h, -1, sizeof(h));cin>>n>>m;int x, y;while(m--){cin>>x>>y;add(x, y);}bfs(1);return 0;
}
拓扑排序
有向无环图也是拓扑图
入度:有多少条边指向自己
出度:有多少条边出去
有向图的拓扑序列

入度为0就是起点,出度为0就是终点
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int q[N], hh, tt = -1;
int n, m;
int r[N]; //存储入度void add(int a, int b){e[idx] = b;ne[idx] = h[a];h[a] = idx;idx++;
}void bfs(){//判断哪些点入度为0for(int i = 1; i <= n; i++)if(!r[i]) q[++tt] = i;while(hh <= tt){int t = q[hh++];for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];r[j]--;if(!r[j]) q[++tt] = j;}}if(tt == n - 1){for(int i = 0; i <= tt; i++) cout<<q[i]<<" ";}else cout<<-1;
}int main(){memset(h, -1, sizeof(h));cin>>n>>m;int x, y;while(m--){cin>>x>>y;add(x, y);r[y]++;}bfs();return 0;
}
最短路
帮助理解
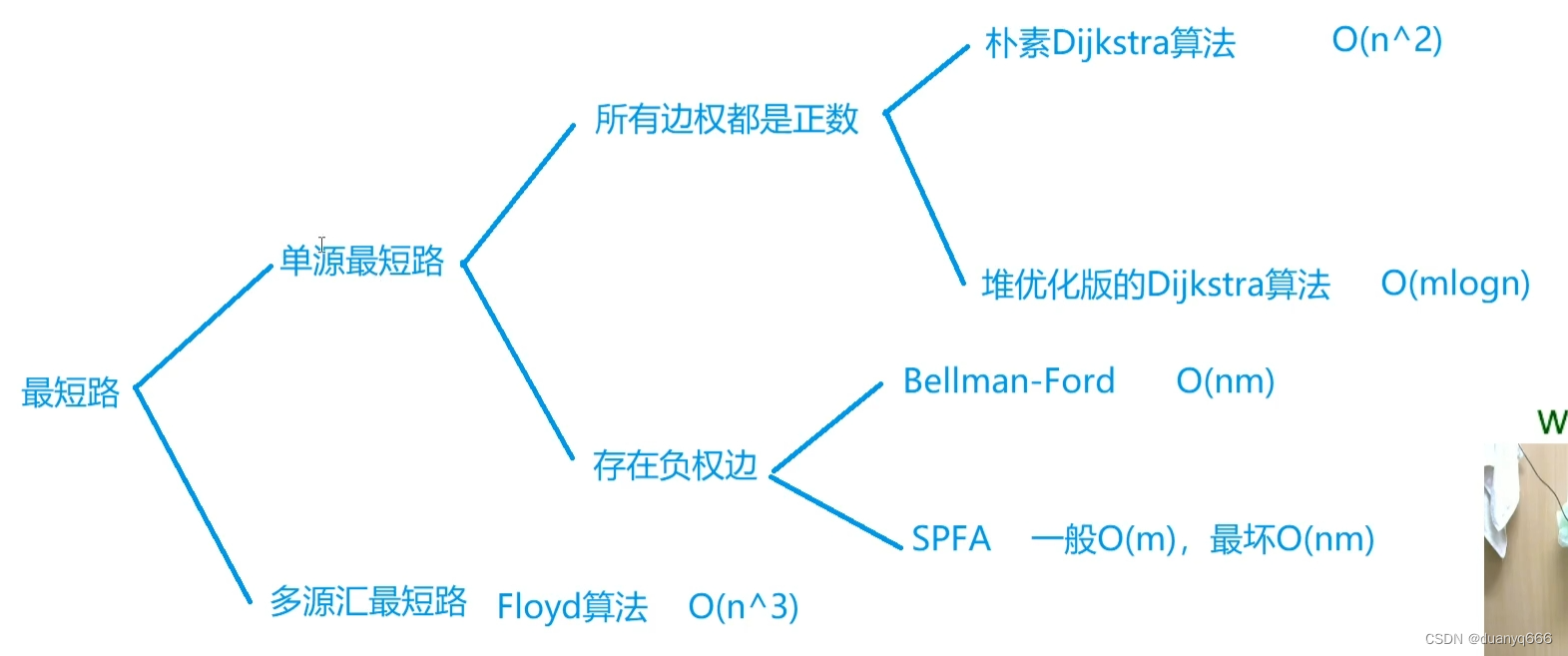
Dijkstra
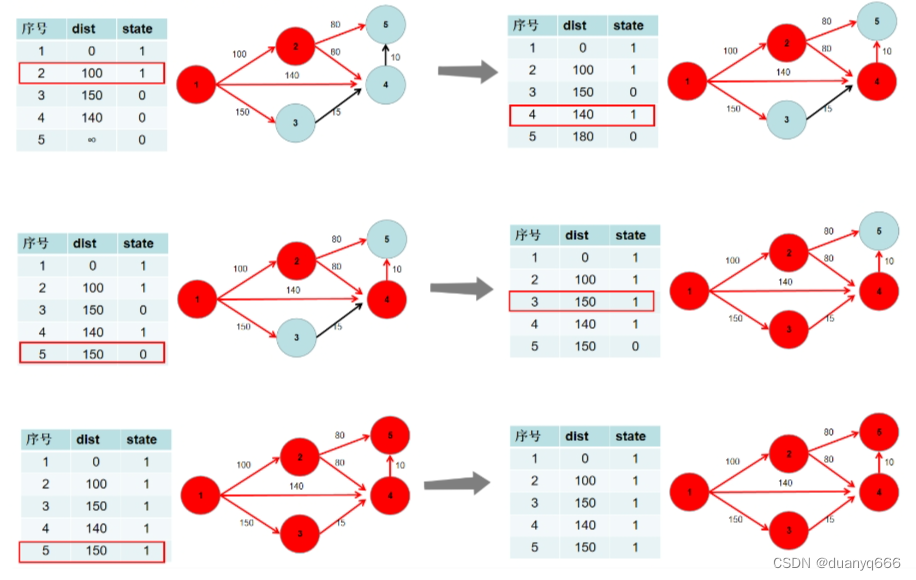
Dijkstra求最短路 I
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;
int g[N][N], d[N], b[N];
int n, m;void dijkstra(int u){memset(d, 0x3f, sizeof(d));d[u] = 0;for(int i = 0; i < n; i++){int t = -1;for(int j = 1; j <= n; j++)if(!b[j] && (t == -1 || d[t] > d[j])) t = j;b[t] = 1;for(int j = 1; j <= n; j++)d[j] = min(d[j], d[t] + g[t][j]);}cout<<((d[n] == 0x3f3f3f3f) ? -1 : d[n]);
}int main(){memset(g, 0x3f, sizeof(g));cin>>n>>m;int x, y, z;while(m--){cin>>x>>y>>z;g[x][y] = min(g[x][y], z);}dijkstra(1);return 0;
}
Dijkstra求最短路 II
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 2e5;
int h[N], e[N], ne[N], w[N], idx; //w[i]存储上个点到i的距离
int d[N], b[N];
int n, m;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q; //小根堆,第一个元素存储距离,第二个元素存储下标void add(int x, int y, int z){e[idx] = y;w[idx] = z;ne[idx] = h[x];h[x] = idx;idx++;
}void dijkstra(int u){memset(d, 0x3f, sizeof(d));d[u] = 0;q.push(make_pair(0, 1));while(q.size()){auto t = q.top();q.pop();int x = t.first, y = t.second;if(b[y]) continue; //如果遍历过就退出b[y] = 1;for(int i = h[y]; i != -1; i = ne[i]){int j = e[i];if(d[j] > x + w[i]){d[j] = x + w[i];q.push(make_pair(d[j], j));}}}cout<<(d[n] == 0x3f3f3f3f ? -1 : d[n]);
}int main(){memset(h, -1, sizeof(h));cin>>n>>m;int x, y, z;while(m--){cin>>x>>y>>z;add(x, y, z);}dijkstra(1);return 0;
}
增加点权,求有多少条最短路
题目链接
#include<iostream>
#include<cstring>
using namespace std;
int g[505][505], dis[505], st[505];
int a[505], paths[505], teams[505];
int n, m, c1, c2;void dj(int u){teams[u] = a[u];paths[u] = 1;dis[u] = 0;for(int j = 0; j < n; j++){int t = -1;for(int i = 0; i < n; i++){if(!st[i] && (t == -1 || dis[t] > dis[i])){t = i;}}st[t] = 1;for(int i = 0; i < n; i++){if(dis[i] > dis[t] + g[t][i]){dis[i] = dis[t] + g[t][i]; paths[i] = paths[t]; //继承路径条数teams[i] = teams[t] + a[i]; //更新救援队人数}else if(dis[i] == dis[t] + g[t][i]){if(teams[i] < teams[t] + a[i]){teams[i] = teams[t] + a[i]; //选救援队人数更多的} paths[i] += paths[t]; //累加路径条数}}}
}int main(){memset(g, 0x3f, sizeof(g));cin>>n>>m>>c1>>c2;for(int i = 0; i < n; i++) cin>>a[i];while(m--){int x, y, z;cin>>x>>y>>z;g[x][y] = g[y][x] = min(g[x][y], z);}memset(dis, 0x3f, sizeof(dis));dj(c1);cout<<paths[c2]<<" "<<teams[c2];return 0;
}
增加边权,求花费最少
题目链接
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
int g[505][505], dis[505], st[505];
int cost[505][505], c[505], pre[505];
vector<int> path;
int n, m, s, d;void dj(int u){dis[u] = 0;c[u] = 0;for(int i = 0; i < n; i++){int t = -1;for(int j = 0; j < n; j++){if(!st[j] && (t == -1 || dis[t] > dis[j])){t = j;}}st[t] = 1;for(int j = 0; j < n; j++){if(dis[j] > dis[t] + g[t][j]){pre[j] = t;dis[j] = dis[t] + g[t][j];c[j] = c[t] + cost[t][j];}else if(dis[j] == dis[t] + g[t][j] && c[j] > c[t] + cost[t][j]){pre[j] = t;c[j] = c[t] + cost[t][j];}}}
}int main(){memset(g, 0x3f, sizeof(g));memset(dis, 0x3f, sizeof(dis));memset(c, 0x3f, sizeof(c));memset(cost, 0x3f, sizeof(cost));cin>>n>>m>>s>>d;while(m--){int x, y, z, h;cin>>x>>y>>z>>h;g[x][y] = g[y][x] = min(g[x][y], z);cost[x][y] = cost[y][x] = min(cost[x][y], h);}for(int i = 0; i < n; i++) pre[i] = i;dj(s);int q = d;while(q != s){path.push_back(q);q = pre[q];}path.push_back(s);int p = path.size();for(int i = p - 1; i >= 0; i--) cout<<path[i]<<" ";cout<<dis[d]<<" "<<c[d];return 0;
}
bellman-ford
有边数限制的最短路
如果负环在1到n的路径上,那就不存在最短路
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510, M = 1e4 + 10;
int d[N], b[N]; //b数组备份
int n, m, k;
struct E{int x, y, z;
}e[M];void bellman_ford(int u){memset(d, 0x3f, sizeof(d));d[u] = 0;//最多k条边for(int i = 0; i < k; i++){//每次只更新一条串联路径,防止更新了多条串联路径memcpy(b, d, sizeof(d));for(int j = 0; j < m; j++){int x = e[j].x, y = e[j].y, z = e[j].z;d[y] = min(d[y], b[x] + z);}}if(d[n] > 0x3f3f3f3f / 2) cout<<"impossible";else cout<<d[n];
}int main(){cin>>n>>m>>k;int x, y, z;for(int i = 0; i < m; i++){cin>>x>>y>>z;e[i] = {x, y, z};}bellman_ford(1);return 0;
}
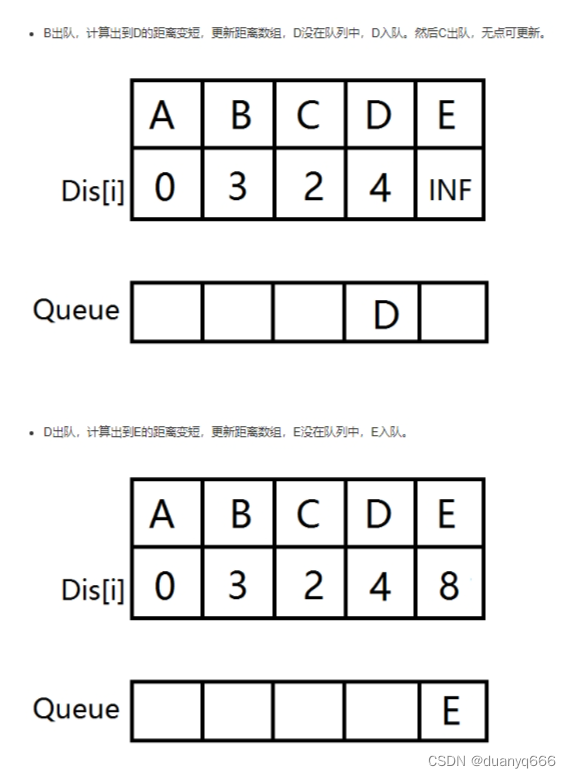
spfa
spfa求最短路

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], w[N], idx;
int dis[N], st[N];
int q[N], hh, tt = -1;
int n, m;void add(int x, int y, int z){e[idx] = y;w[idx] = z;ne[idx] = h[x];h[x] = idx;idx++;
}void spfa(int u){memset(dis, 0x3f, sizeof(dis));dis[u] = 0;q[++tt] = u;st[u] = 1;while(hh <= tt){int t = q[hh++];//有环,所以可能一个点会遍历两次st[t] = 0;for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(dis[j] > dis[t] + w[i]){dis[j] = dis[t] + w[i];if(!st[j]){q[++tt] = j;st[j] = 1;}}}}if(dis[n] == 0x3f3f3f3f) cout<<"impossible";else cout<<dis[n];
}int main(){memset(h, -1, sizeof(h));cin>>n>>m;int x, y, z;for(int i = 0; i < m; i++){cin>>x>>y>>z;add(x, y, z);}spfa(1);return 0;
}
spfa判断负环
#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e3 + 10, M = 1e4 + 10;;
int h[N], e[M], ne[M], w[M], idx;
int dis[N], st[N], cnt[N];
int q[N * N], hh, tt = -1; //有环的时候,一个元素可能会一直插入队列,所以要开N * N
int n, m;void add(int x, int y, int z){e[idx] = y;w[idx] = z;ne[idx] = h[x];h[x] = idx;idx++;
}void spfa(){//存在的负权回路,不一定从1开始for(int i = 1; i <= n; i++){q[++tt] = i;st[i] = 1;}while(hh <= tt){int t = q[hh++];//有环,所以可能一个点会遍历两次st[t] = 0;for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(dis[j] > dis[t] + w[i]){dis[j] = dis[t] + w[i];cnt[j] = cnt[t] + 1;if(cnt[j] >= n){cout<<"Yes";return;}if(!st[j]){q[++tt] = j;st[j] = 1;}}}}cout<<"No";
}int main(){memset(h, -1, sizeof(h));cin>>n>>m;int x, y, z;for(int i = 0; i < m; i++){cin>>x>>y>>z;add(x, y, z);}spfa();return 0;
}
Floyd
Floyd求最短路
f(k, i, j) = f(k - 1, i, k) + f(k - 1, k, j);
#include<iostream>
using namespace std;
const int N = 210;
int f[N][N];
int n, m, k;void floyd(){for(int k = 1; k <= n; k++)for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}int main(){cin>>n>>m>>k;for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)if(i == j) f[i][j] = 0;else f[i][j] = 0x3f3f3f3f;int x, y, z;for(int i = 1; i <= m; i++){cin>>x>>y>>z;f[x][y] = min(f[x][y], z);}floyd();for(int i = 1; i <= k; i++){cin>>x>>y;//可能存在负权边if(f[x][y] > 0x3f3f3f3f / 2) cout<<"impossible"<<endl;else cout<<f[x][y]<<endl;}return 0;
}
最小生成树

Prim
Kruskal
二分图
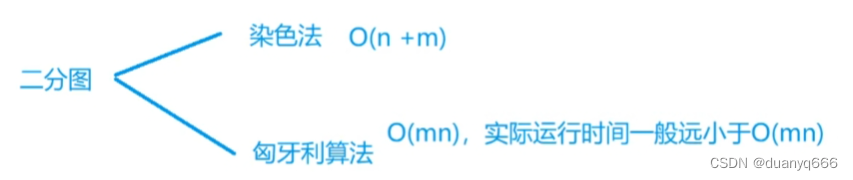
染色法判定二分图
匈牙利算法
相关文章:

三、搜索与图论
DFS 排列数字 #include<iostream> using namespace std; const int N 10; int a[N], b[N]; int n;void dfs(int u){if(u > n){for(int i 1; i < n; i)cout<<a[i]<<" ";cout<<endl;return;}for(int i 1; i < n; i){if(!b[i]){b[…...
【翻译】Processing安卓模式的安装使用及打包发布(内含中文版截图)
原文链接在下面的每一章的最前面。 原文有三篇,译者不知道贴哪篇了,这篇干脆标了原创。。 译者声明:本文原文来自于GNU协议支持下的项目,具备开源二改授权,可翻译后公开。 文章目录 Install(安装࿰…...
MATLAB图像处理——边缘检测及图像分割算法
1.检测图像中的线段 clear clc Iimread(1.jpg);%读入图像 Irgb2gray(I); %转换为灰度图像 h1[-1, -1. -1; 2, 2, 2; -1, -1, -1]; %模板 h2[-1, -1, 2; -1, 2, -1; 2, -1, -1]; h3[-1, 2, -1; -1, 2, -1; -1, 2, -1]; h4[2, -1, -1; -1, 2, -1; -1, -1, 2]; J1imfilter(I, h1)…...

探索设计模式:原型模式深入解析
探索设计模式:原型模式深入解析 设计模式是软件开发中用于解决常见问题的标准解决方案。它们不仅能提高代码的可维护性和可复用性,还能让其他开发者更容易理解你的设计决策。今天,我们将聚焦于创建型模式之一的原型模式(Prototyp…...

IAR报错解决:Fatal Error[Pe1696]: cannot open source file “zcl_ha.h“
报错信息 Fatal Error[Pe1696]: cannot open source file "zcl_ha.h" K:\Z-Stack 3.0.2\Projects\zstack\Practice\SampleSwitch\Source\zcl_samplesw_data.c 51 意思是找不到zcl_ha.h文件 找不到的理由可能是我把例程复制了一份到别的文件目录下,少复制…...
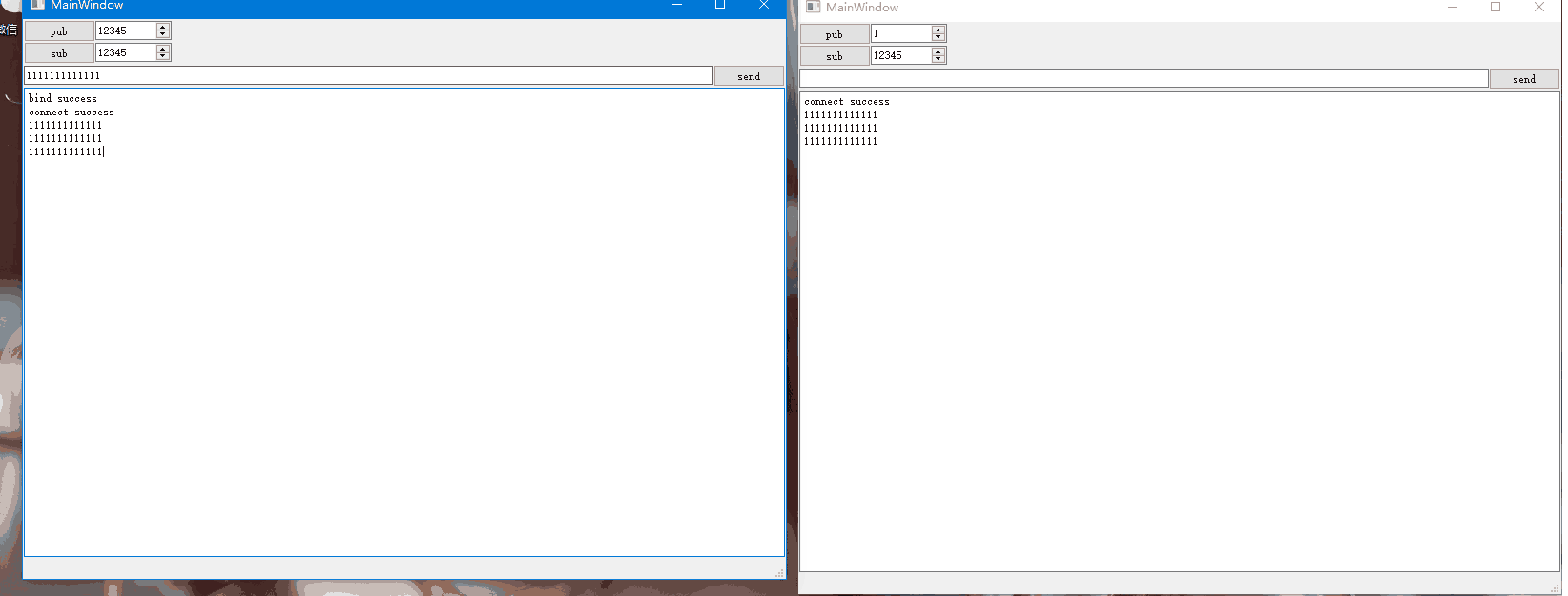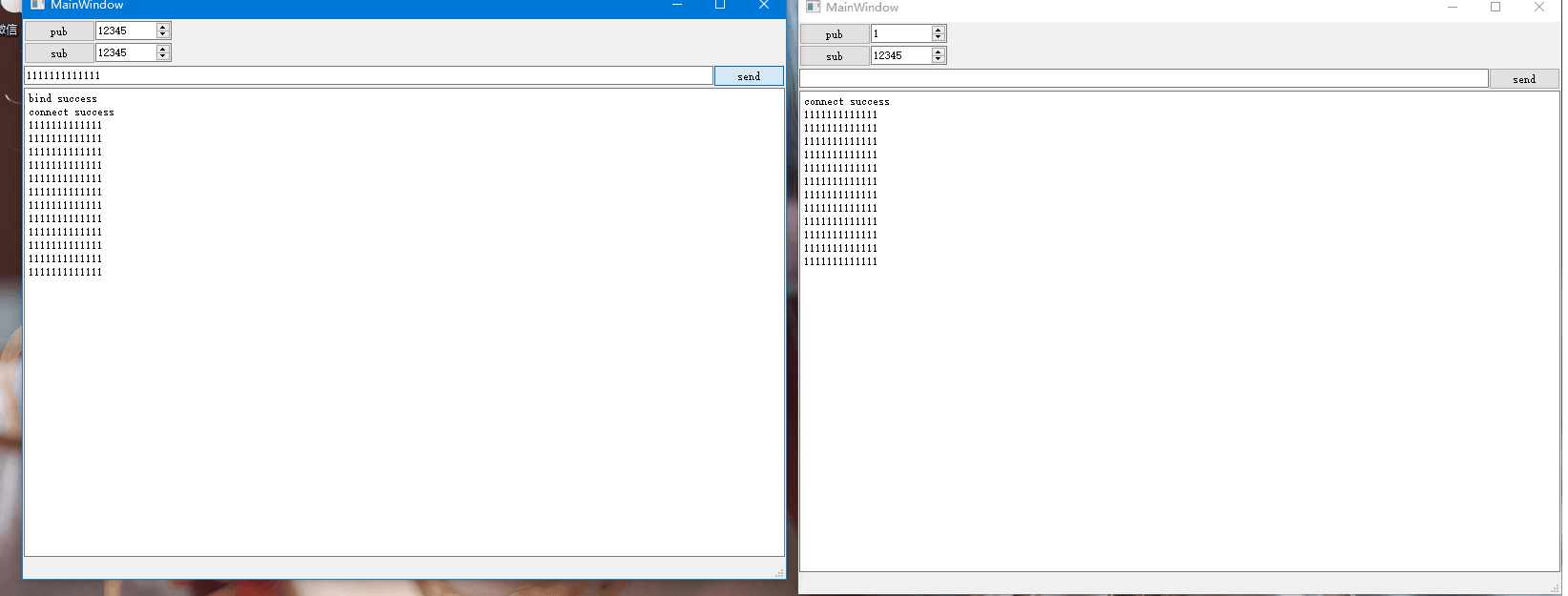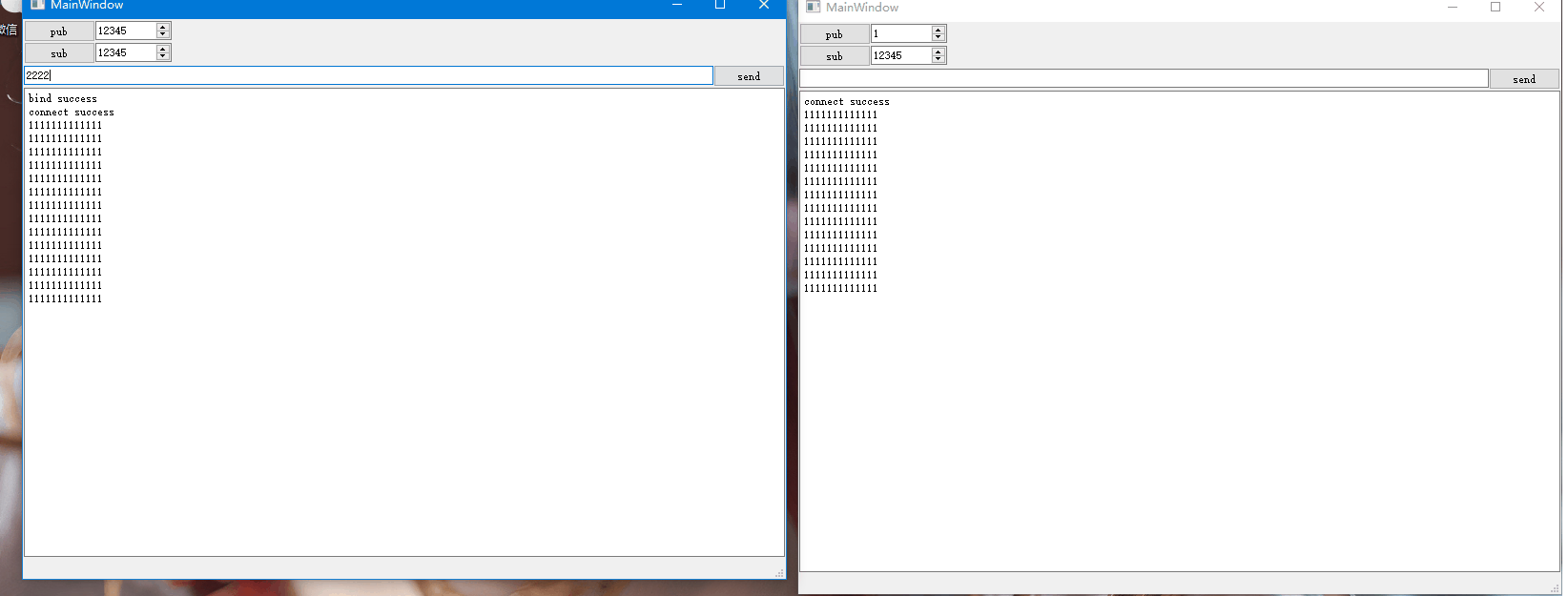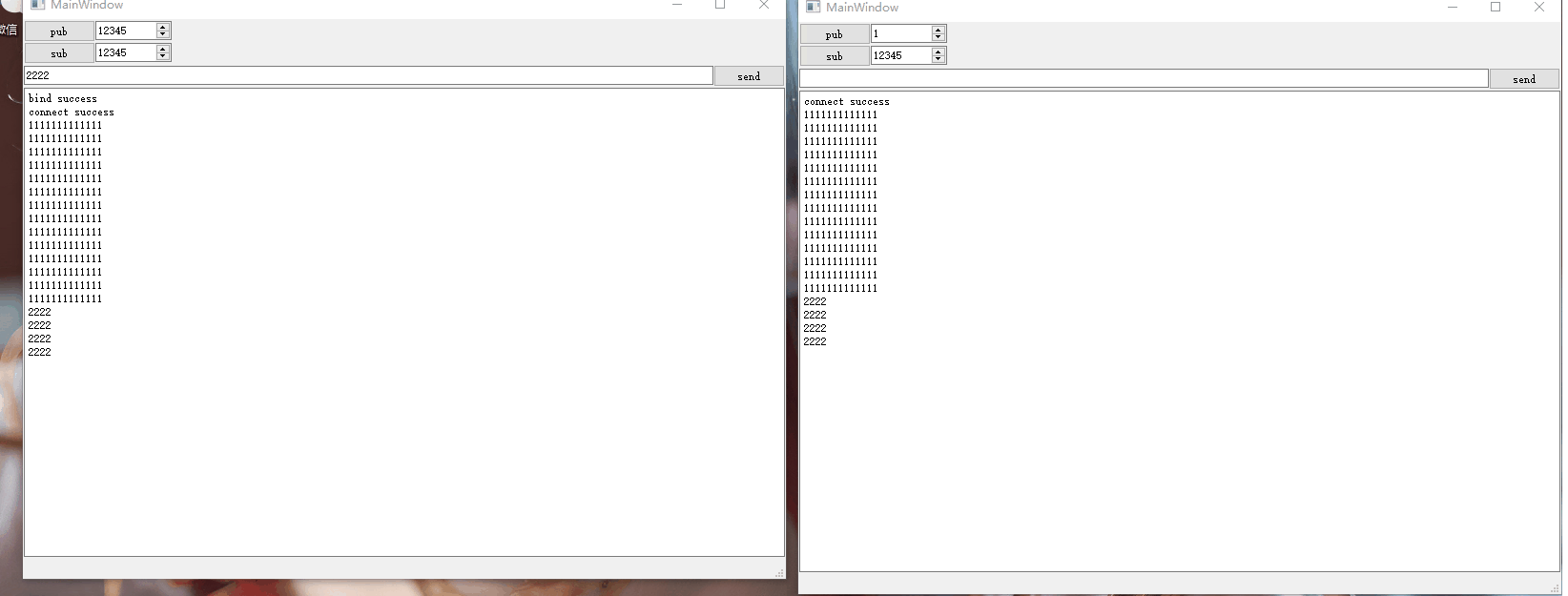
Qt网络编程-ZMQ的使用
不同主机或者相同主机中不同进程之间可以借助网络通信相互进行数据交互,网络通信实现了进程之间的通信。比如两个进程之间需要借助UDP进行单播通信,则双方需要知道对方的IP和端口,假设两者不在同一主机中,如下示意图: …...

如何清理Docker占用的磁盘空间?
在Docker中,随着时间的推移,占用的磁盘空间可能会不断增加。为了保持系统的稳定性和性能,定期清理Docker占用的磁盘空间非常重要。下面将介绍一些清理Docker磁盘空间的方法。 一、清理无用的容器 有时候,我们可能会运行一些临时…...

从零开始学HCIA之NAT基本工作原理
1、NAT设计之初的目的是解决IP地址不足的问题,慢慢地其作用发展到隐藏内部地址、实现服务器负载均衡、完成端口地址转换等功能。 2、NAT完成将IP报文报头中的IP地址转换为另一个IP地址的过程,主要用于实现内部网络访问外部网络的功能。 3、NAT功能一般…...

Day40- 动态规划part08
一、单词拆分 题目一:139. 单词拆分 139. 单词拆分 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以…...

论文笔记:相似感知的多模态假新闻检测
整理了RecSys2020 Progressive Layered Extraction : A Novel Multi-Task Learning Model for Personalized Recommendations)论文的阅读笔记 背景模型实验 论文地址:SAFE 背景 在此之前,对利用新闻文章中文本信息和视觉信息之间的关系(相似…...

5G技术对物联网的影响
随着数字化转型的加速,5G技术作为通信领域的一次重大革新,正在对物联网(IoT)产生深远的影响。对于刚入行的朋友们来说,理解5G技术及其对物联网应用的意义,是把握行业发展趋势的关键。 让我们简单了解什么是…...
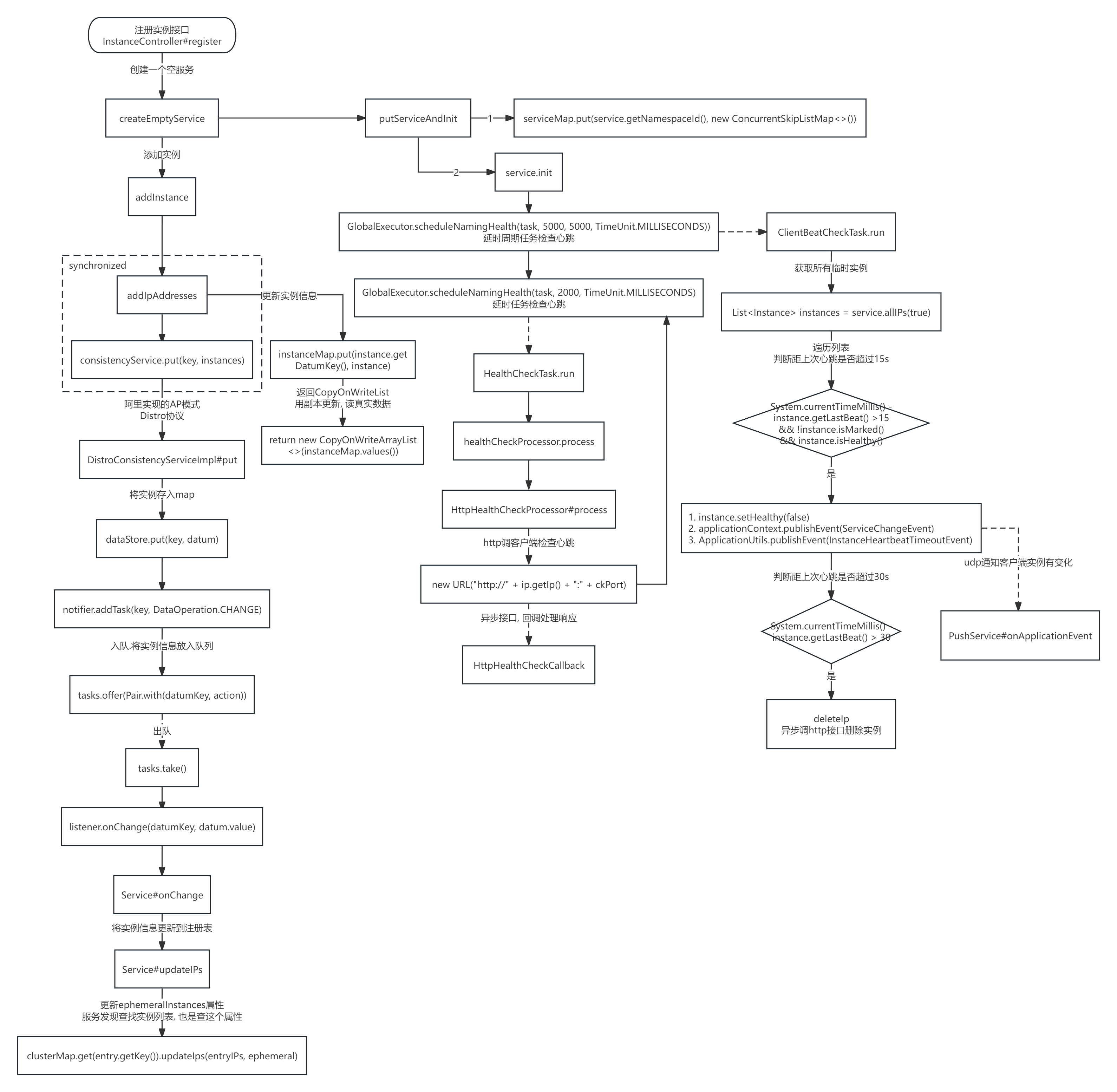
Nacos1.X源码解读(待完善)
目录 下载源码 注册服务 客户端注册流程 注册接口API 服务端处理注册请求 设计亮点 服务端流程图 下载源码 1. 克隆git地址到本地 # 下载nacos源码 git clone https://github.com/alibaba/nacos.git 2. 切换分支到1.4.7, maven编译(3.5.1) 3. 找到启动类com.alibaba.na…...

算法之双指针系列1
目录 一:双指针的介绍 1:快慢指针 2:对撞指针 二:对撞指针例题讲述 一:双指针的介绍 在做题中常用两种指针,分别为对撞指针与快慢指针。 1:快慢指针 简称为龟兔赛跑算法,它的基…...

苍穹外卖面试题
8. 如何理解分组校验 很多情况下,我们会将校验规则写到实体类中的属性上,而这个实体类有可能作为不同功能方法的参数使用,而不同的功能对象参数对象中属性的要求是不一样的。比如我们在新增和修改一个用户对象时,都会接收User对象…...
【Qt 学习之路】在 Qt 使用 ZeroMQ
文章目录 1、概述2、ZeroMQ介绍2.1、ZeroMQ 是什么2.2、ZeroMQ 主线程与I/O线程2.3、ZeroMQ 4种模型2.4、ZeroMQ 相关地址 3、Qt 使用 ZeroMQ3.1、下载 ZeroMQ3.2、添加 ZeroMQ 库3.3、使用 ZeroMQ3.4、相关 ZeroMQ 案例 1、概述 今天是大年初一,先给大家拜个年&am…...

CI/CD到底是啥?持续集成/持续部署概念解释
前言 大家好,我是chowley,日常工作中,我每天都在接触CI/CD,今天就给出我心中的答案。 在现代软件开发中,持续集成(Continuous Integration,CI)和持续部署(Continuous D…...
)
golang常用库之-disintegration/imaging图片操作(生成缩略图)
文章目录 golang常用库之什么是imaging库导入和使用生成缩略图 golang常用库之 什么是imaging库 官网:https://github.com/disintegration/imaging imaging 是一个 Go 语言的图像处理库,它提供了一组功能丰富的函数和方法,用于进行各种图像…...

CSS 控制 video 标签的控制栏组件的显隐
隐藏下载功能 <video src"" controlsList"nodownload" />controlslist 取值如下(设定多个值则使用空格进行间隔) 如:controlslist"nodownload nofullscreen noremoteplayback"nodownload:取消更多控件弹窗的下载功…...

数据可视化之维恩图 Venn diagram
文章目录 一、前言二、主要内容三、总结 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 维恩图(Venn diagram),也叫文氏图或韦恩图,是一种关系型图表,用于显示元素集合之间的重叠区…...

2024刘谦春晚第二个扑克牌魔术
前言 就是刚才看春晚感觉这个很神奇,虽然第一个咱模仿不过来,第二个全国人民这么多人,包括全场观众都有成功,这肯定是不需要什么技术,那我觉得这个肯定就是数学了,于是我就胡乱分析一通。 正文 首先准备…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...
