###C语言程序设计-----C语言学习(12)#进制间转换,十进制,二进制,八进制,十六进制
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。

计算机处理的所有信息都以二进制形式表示,即数据的存储和计算都采用二进制,同时对于计算机系统所识别的也主要为二进制,如:单片机系统等,所以今天我们分享二进制,八进制,十进制,十六进制,以及进制间的转换。
目录
一. 进制的简单介绍
1.二进制
2.八进制
3.十进制
4.十六进制
二. 进制间转换
1.其他进制转十进制
(1)二进制转十进制
(2)八进制转十进制
(3)十六进制转十进制
2.十进制转其他进制
(1)十进制转二进制
(2)十进制转八进制
(3)十进制转十六进制
一. 进制的简单介绍
进制是一种数学计数系统,用于表示数值。在计算机科学和数字电子中,进制尤为重要,因为计算机只能理解和处理二进制数据。
1.二进制
二进制是一种基础的数字系统,它只有两个数码0和1,可以表示任何数字信息哦。
2.八进制
八进制是一种以8为基数的计数法,它采用0到7这八个数字,并且逢八进一。在计算机科学和电子技术中,八进制常用于表示和处理数字、数据和指令。比如,在计算机系统中,文件和目录的权限通常以八进制形式表示。此外,八进制也常用于UNIX时间戳、文件和存储容量、POSIX文件权限、系统调用操作码以及文件和目录索引节点(iNode)的表示。
与二进制相比,八进制可以减少数字的长度和复杂度,因为每一位八进制数可以对应三位二进制数。这使得八进制在计算机科学中成为一种重要的数制系统。
3.十进制
十进制是我们日常生活中最为熟悉和常用的一种数制系统。它基于10个数字(0-9),并且遵循“逢十进一”的规则。在十进制中,每一位数字的权重是10的幂次,从右向左依次增加。例如,数字“123”可以表示为1×10^2 + 2×10^1 + 3×10^0。
十进制数的特点是直观易懂、易于理解和使用。我们在进行数字的四则运算、货币计算、单位换算以及各种数学应用时,通常都使用十进制数。此外,十进制数也可以方便地与其他进制数进行转换,如二进制、八进制和十六进制等。
与其他进制数相比,十进制数在人类生活和科学计算中占据重要地位。它不仅是我们日常生活和工作中使用的主要数制系统,也是计算机科学和电子技术中不可或缺的一部分。
4.十六进制
十六进制(Hexadecimal)是一种基数为16的计数系统,它采用0到9和A到F这16个数字来表示数值。其中,A到F代表10到15的十进制数。十六进制数的特点是逢16进1,这意味着当某一位的数字达到16时,它会向前一位进位。
在计算机科学和电子技术中,十六进制是一种非常重要的数制系统。由于它使用16个数字来表示数值,因此它比二进制和八进制更加紧凑,能够减少数字的长度和复杂度。这使得十六进制成为表示二进制数据的一种有效方式,特别是在低级编程、内存和存储器管理、网络协议和通信等领域中广泛应用。
十六进制数的表示方式非常直观,可以通过将每四位二进制数转换为一位十六进制数来实现。这种转换方式使得大整数和二进制数据在十六进制下更加易读和处理。此外,十六进制与二进制之间可以方便地进行转换,这也使得它在计算机科学中成为一种重要的数制系统。
二. 进制间转换
1.其他进制转十进制
(1)二进制转十进制
例如对于一个十进制数235,它由个位,十位,百位组成,所以235可以写成2*10^2+3*10^1+5*10^0
则同理对于一个二进制数1011可以写成
1*2^3+0*2^2+1*2^1+1*2^0 得出转换为十进制11
(2)八进制转十进制
首先八进制由01234567来表示,对于八进制数277可写成
2*8^2+7*8^1+7*8^0 得出转换为十进制数191
(3)十六进制转十进制
首先十六进制由0123456789ABCDEF组成,其中ABCDEF分别对应10,11,12,13,14,15,则对于十六进制数2AE可写成
2*16^2+10*16^1+14*16^0 得出转换十进制数686
2.十进制转其他进制
(1)十进制转二进制
十进制转其他进制可采用连除法,如十进制数29
29/2 余1
14/2 余0
7/2 余1
3/2 余1
1/2 余1 (一直连除到结果为0,只有余数为止)
0
此时余数从下到上排列得到二进制数11101
(2)十进制转八进制
例如十进制数900
900/8 余4
112/8 余0
14/8 余6
1/8 余1
0 此时得到转换得八进制数1604
(3)十进制转十六进制
例如十进制数2717
2717/16 余13
169/16 余9
10/16 余10
0 此时通过转换为十六进制为A9D
感谢老铁的浏览,希望老铁可以一键三连加个关注,您的支持和鼓励是我前进的动力,后续会分享更多学习编程的内容。

相关文章:

###C语言程序设计-----C语言学习(12)#进制间转换,十进制,二进制,八进制,十六进制
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 计算机处理的所有信息都以二进制形式表示,即数据的存储和计算都采…...

锐捷设备常用命令
一、命令模式 命令行主要有用户模式、特权模式、全局模式、VLAN模式、接口模式、线程模式 switch> "用户模式"switch# "特权模式"switch(config) "全局模式"switch(conf…...

python:lxml 读目录.txt文件,用 xmltodict 转换为json数据,生成jstree所需的文件
请参阅:java : pdfbox 读取 PDF文件内书签 请注意:书的目录.txt 编码:UTF-8,推荐用 Notepad 转换编码。 pip install lxml ; lxml-5.1.0-cp310-cp310-win_amd64.whl (3.9 MB) pip install xmltodict ; lxml 读目录.txt文件&…...

【Spring】Spring 对 Ioc 的实现
一、Ioc 控制反转 控制反转是一种思想 控制反转是为了降低程序耦合度,提高程序扩展力,达到 OCP 原则,达到 DIP 原则 控制反转,反转的是什么? 将对象的创建权利交出去,交给第三方容器负责 将对象和对象之…...

QT学习文件操作类 QFile
(一)QFile QFile 是 Qt 框架中用于文件处理的一个类。它提供了读取和写入文件的功能,支持文本和二进制文件。QFile 继承自 QIODevice ,因此它可以像其他 IO 设备一样使用。 (1)主要功能 1. 文件读写…...

VOL_常用记录!!
目录 前端1.js如何获取当前时间(yy-MM-dd HH:MM:SS)2.http请求3.grid扩展js常用 后端1.待补充 前端 1.js如何获取当前时间(yy-MM-dd HH:MM:SS) getCurrentTime() {const now new Date();return ${now.getFullYear()}-${(now.getMonth() 1).toString().padStart(2, "0&…...
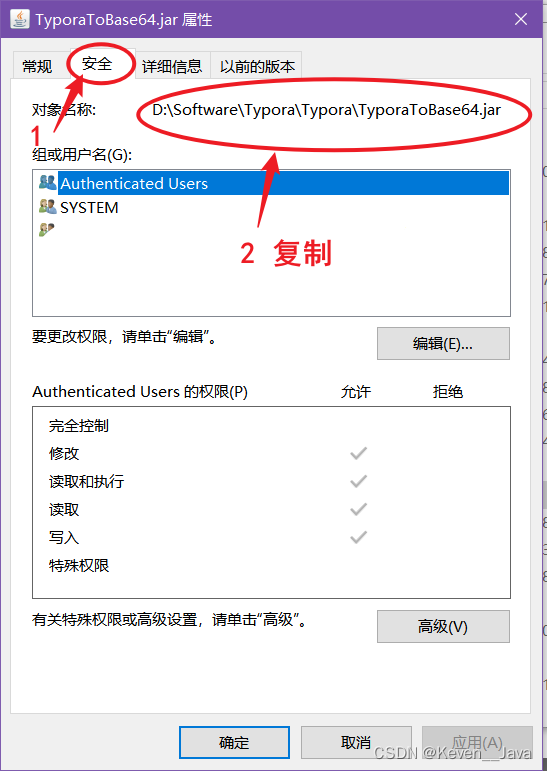
解决Typora导出HTML不显示图片
解决Typora导出HTML不显示图片 产生原因 Typora导出HTML不显示图片,可能时图片存放在我们的硬盘中。 我们可以将markdown中的图片转化为base64格式,嵌入到html中。 解决步骤 首先,下载 TyporaToBase64.jar 密码:45jq 其次,将…...
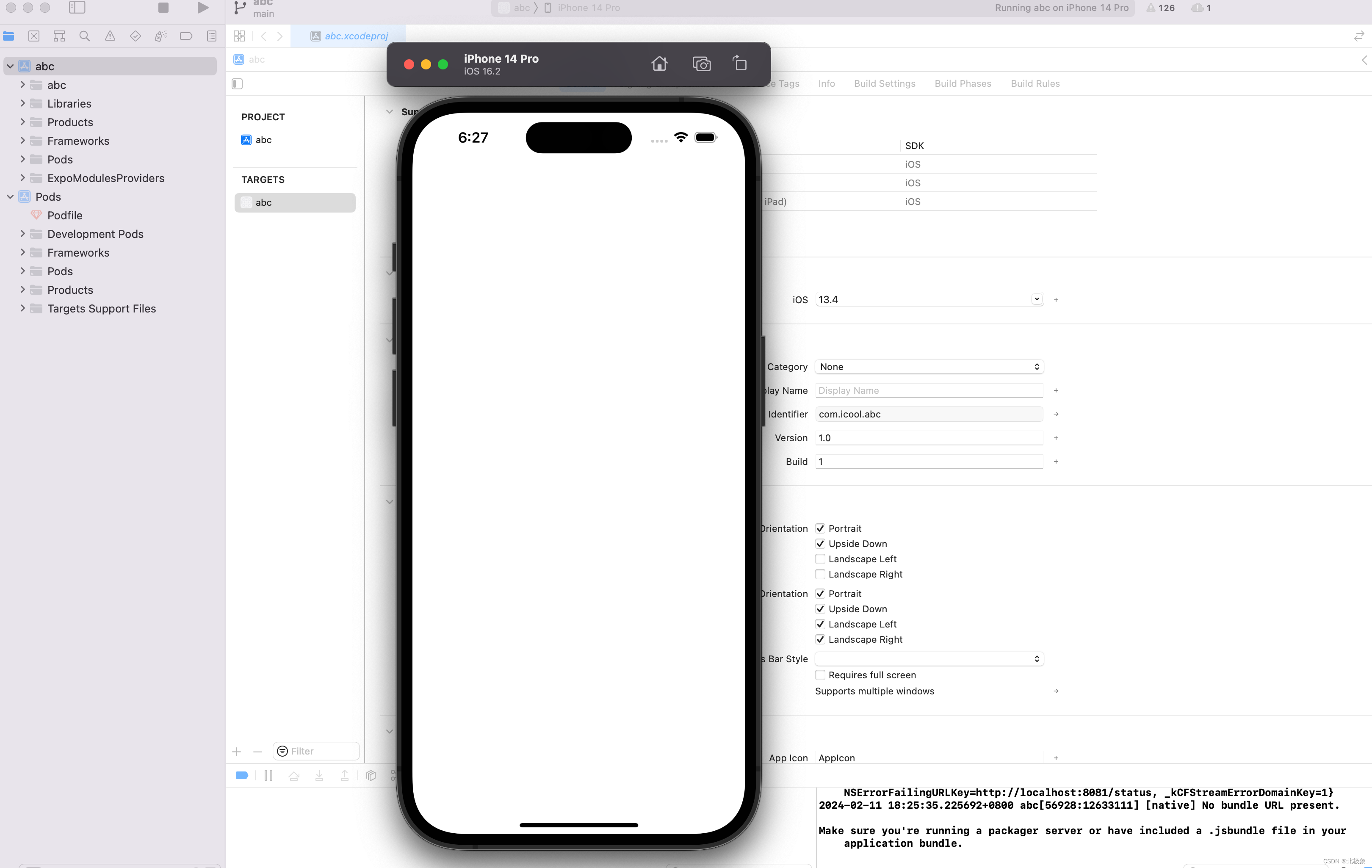
React Native开发iOS实战录
文章目录 背景环境准备主要工具xcode安装安装CocoaPods 基本步骤采用Expo go运行iOS模拟器运行安装在真机上测试发布到苹果商店 常见问题ruby3在macOS上编译失败import of module ‘glog.glog.log_severity’ appears within namespace ‘google’yarn网络问题pod安装失败unabl…...

C++局部变量与全局变量
在C中,可以为函数的参数指定默认值。这样做的好处是在调用函数时,如果没有提供对应的参数,那么将会使用默认值。 下面是一个求2个或3个数中最大数的函数的示例,其中使用了默认参数: #include <iostream> using…...
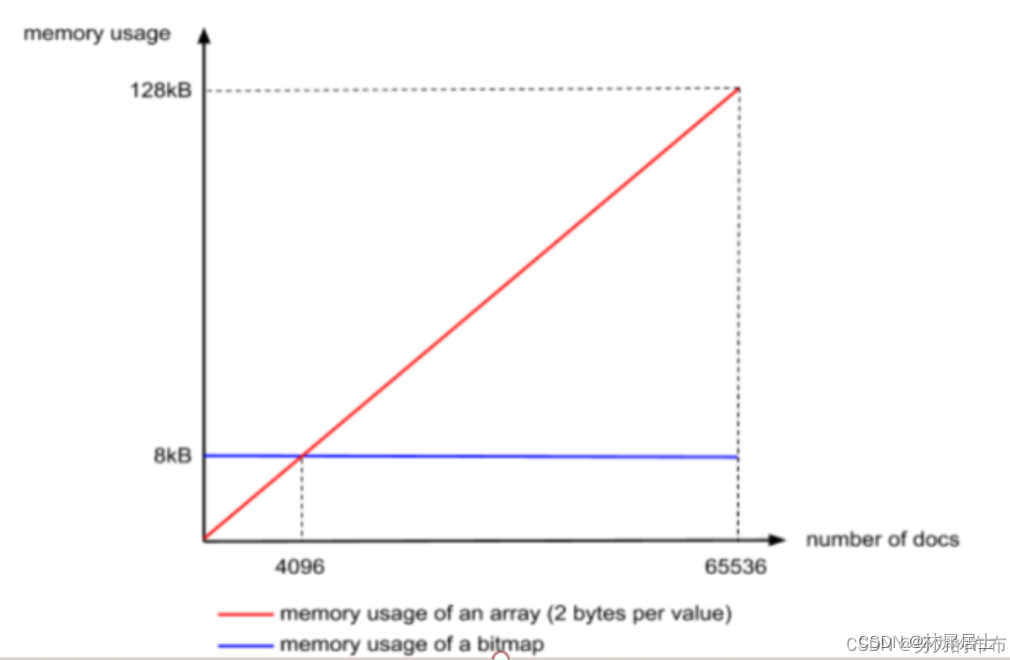
深入理解ES的倒排索引
目录 数据写入过程 词项字典 term dictionary 倒排表 posting list FOR算法 RBM算法 ArrayContainer BitMapContainer 词项索引 term index 在Elasticsearch中,倒排索引的设计无疑是惊为天人的,下面看下倒排索引的结构。 倒排索引分为词项索引【…...

HTML世界之第一重天
一、HTML 元素 注:HTML 文档由 HTML 元素定义。 1.HTML 元素 开始标签 * 元素内容 结束标签 * <p> 这是一个段落 </p> <a href"default.htm"> 这是一个链接 </a> <br> 换行 开始标签常被称为起始标签&…...

docker run报 docker: Error response from daemon: no command specified.
docker run报 docker: Error response from daemon: no command specified. 1. export出mysql的container为tar, 拷贝到另一台虚拟机, import该tar为image, docker run该image时报 docker: Error response from daemon: no command specified. 时间240211 export出mysql的con…...

vue3 之 商城项目—详情页
整体认识 路由配置 准备组件模版 <script setup></script><template><div class"xtx-goods-page"><div class"container"><div class"bread-container"><el-breadcrumb separator">">&…...

Linux笔记之Docker进行镜像备份与迁移
Linux笔记之Docker进行镜像备份与迁移 ——2024-02-11 code review! 文章目录 Linux笔记之Docker进行镜像备份与迁移1. 导出容器文件系统为 tar 归档文件2. 将 tar 归档文件导入为新的 Docker 镜像3. 运行新的 Docker 镜像并创建容器 1. 导出容器文件系统为 tar 归档文件 要导…...
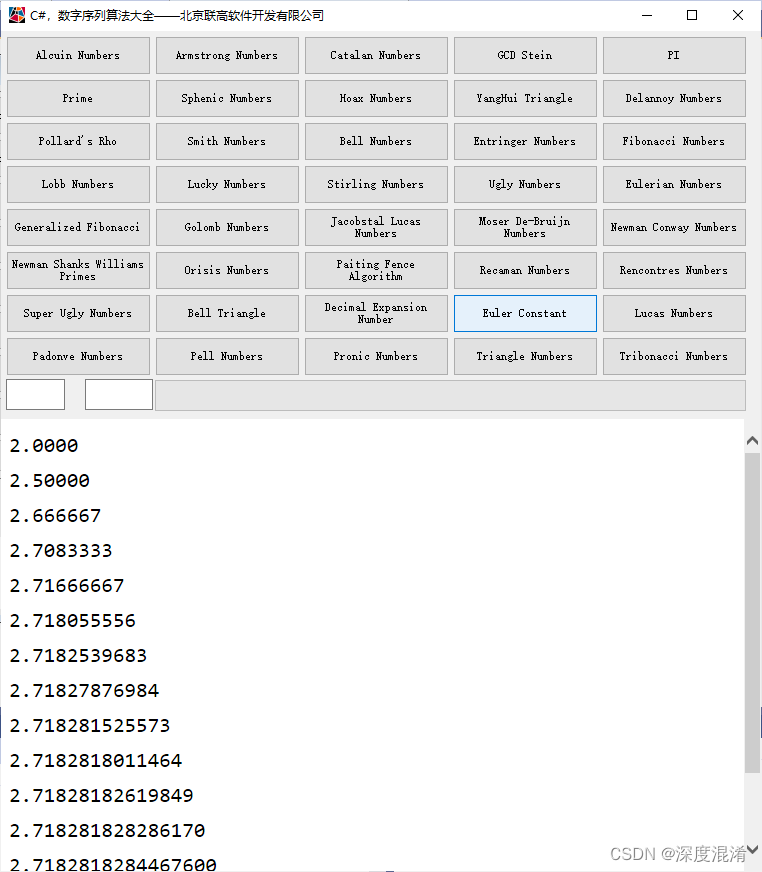
C#,欧拉常数(Euler Constant)的算法与源代码
1 欧拉常数 欧拉常数最先由瑞士数学家莱昂哈德 欧拉 (Leonhard Euler) 在1735年发表的文章《De Progressionibus harmonicus observationes》中定义。欧拉曾经使用γ作为它的符号,并计算出了它的前6位,1761年他又将该值计算到了16位 。 欧拉常数最先由瑞…...

asio监听eventfd
c - Does BOOST asio supports eventfd? like epoll - Stack Overflow asio的官方example并没有asio监听eventfd的例子,但asio支持posix::stream_descriptor, 如果将eventfd包装成posix::stream_descriptor,并注册到io_context里…...

《统计学简易速速上手小册》第9章:统计学在现代科技中的应用(2024 最新版)
文章目录 9.1 统计学与大数据9.1.1 基础知识9.1.2 主要案例:社交媒体情感分析9.1.3 拓展案例 1:电商销售预测9.1.4 拓展案例 2:实时交通流量分析 9.2 统计学在机器学习和人工智能中的应用9.2.1 基础知识9.2.2 主要案例:预测客户流…...
问题排查利器 - 分布式 trace
在分布式系统开发中,系统间的调用往往会横跨多个应用之间的接口。负责的调用链路也导致了,当线上环境出现问题时,例如请求失败、延迟增加或错误发生,我们无法第一时间确定是哪个环节出了问题,这给故障排查和修复带来了…...
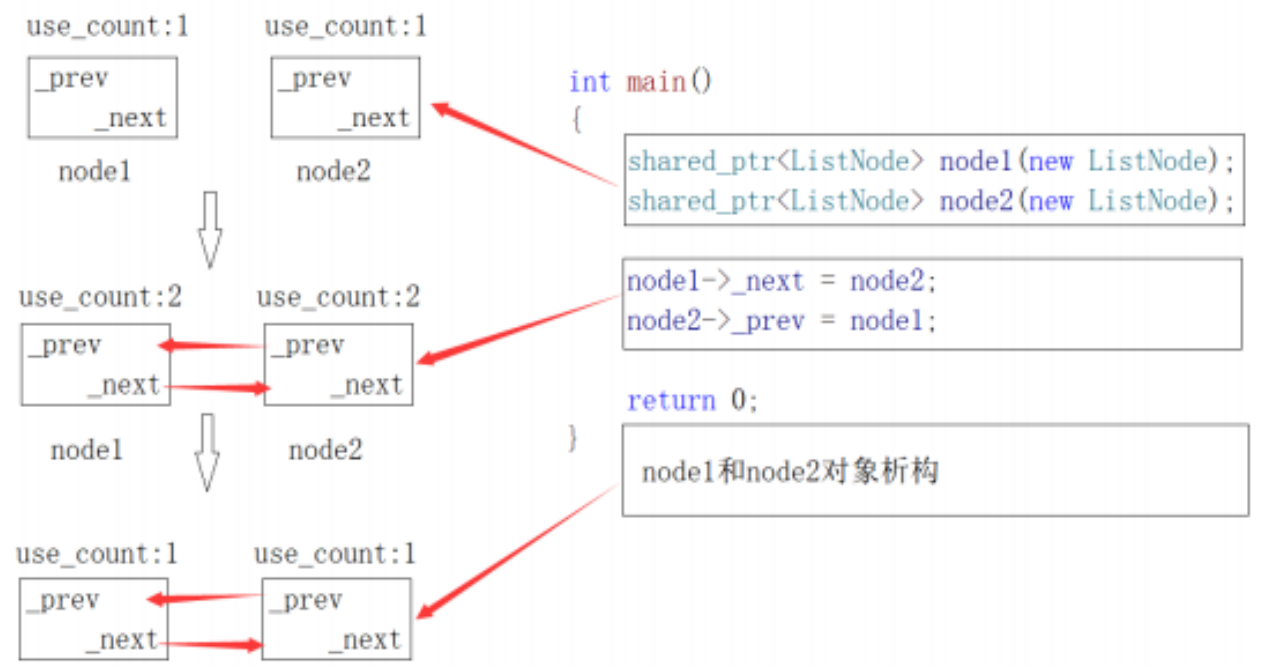
C++进阶(十四)智能指针
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、为什么需要智能指针?二、内存泄漏1、 什么是内存泄漏,内存泄漏的危…...

GPT最新进展:推出视频功能!迭代即将来临!
随着人工智能的不断进步,ChatGPT正准备以其全新的视频功能大跃进,同时,备受期待的GPT-5也即将在今年露面,预示着AI领域即将迎来一场变革。 在最近一期充满激情的Unconfuse Me播客中,OpenAI的首席执行官Sam Altman与技…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
