C#,欧拉常数(Euler Constant)的算法与源代码

1 欧拉常数
欧拉常数最先由瑞士数学家莱昂哈德· 欧拉 (Leonhard Euler) 在1735年发表的文章《De Progressionibus harmonicus observationes》中定义。欧拉曾经使用γ作为它的符号,并计算出了它的前6位,1761年他又将该值计算到了16位 。
欧拉常数最先由瑞士数学家莱昂哈德·欧拉(Leonhard Euler)在1735年发表的文章 De Progressionibus harmonicus observationes 中定义。欧拉曾经使用C作为它的符号,并计算出了它的前6位小数。1761年他又将该值计算到了16位小数。1790年,意大利数学家马歇罗尼(Lorenzo Mascheroni)引入了γ作为这个常数的符号,并将该常数计算到小数点后32位。但后来的计算显示他在第20位的时候出现了错误。欧拉数以世界著名数学家欧拉名字命名;还有一个鲜为人知的名字纳皮尔常数,用来纪念苏格兰数学家约翰·纳皮尔 (John Napier) 引进对数 。
2 计算结果
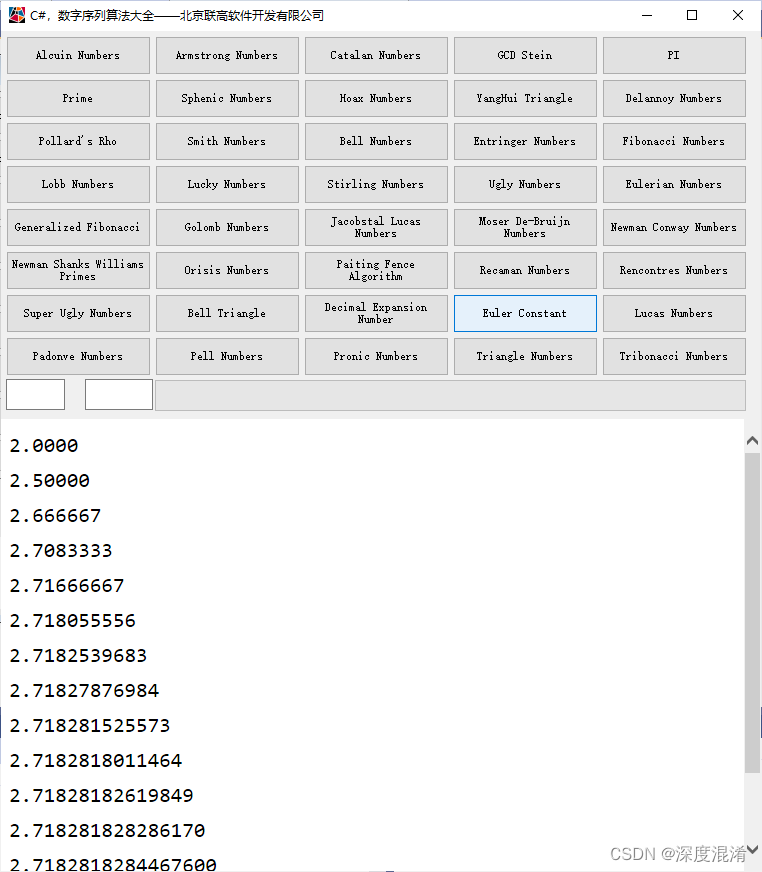
3 源程序
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
private static double doubleFactorial(int n)
{
if (n == 1) return 1;
else return n * doubleFactorial(n - 1);
}
public static double Euler_Constant(int n)
{
if (n == 0) return 1;
else return (1 / doubleFactorial(n) + Euler_Constant(n - 1));
}
}
}
欧拉常数(Euler-Mascheroni constant)
欧拉-马歇罗尼常数(Euler-Mascheroni constant)是一个主要应用于数论的数学常数。它的定义是调和级数与自然对数的差值。
学过高等数学的人都知道,调和级数S=1+1/2+1/3+……是发散的,证明如下:
由于ln(1+1/n)<1/n (n=1,2,3,…)
于是调和级数的前n项部分和满足
Sn=1+1/2+1/3+…+1/n>ln(1+1)+ln(1+1/2)+ln(1+1/3)+…+ln(1+1/n)
=ln2+ln(3/2)+ln(4/3)+…+ln[(n+1)/n]
=ln[2*3/2*4/3*…*(n+1)/n]=ln(n+1)
由于
lim Sn(n→∞)≥lim ln(n+1)(n→∞)=+∞
所以Sn的极限不存在,调和级数发散。
但极限S=lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)却存在,因为
Sn=1+1/2+1/3+…+1/n-ln(n)>ln(1+1)+ln(1+1/2)+ln(1+1/3)+…+ln(1+1/n)-ln(n)
=ln(n+1)-ln(n)=ln(1+1/n)
由于
lim Sn(n→∞)≥lim ln(1+1/n)(n→∞)=0
因此Sn有下界
而
Sn-S(n+1)=1+1/2+1/3+…+1/n-ln(n)-[1+1/2+1/3+…+1/(n+1)-ln(n+1)]
=ln(n+1)-ln(n)-1/(n+1)=ln(1+1/n)-1/(n+1)
将ln(1+1/n)展开,取其前两项,由于舍弃的项之和大于0,故
ln(1+1/n)-1/(n+1)>1/n-1/(2n^2)-1/(n+1)=1/(n^2+n)-1/(2n^2)>0
即ln(1+1/n)-1/(n+1)>0,所以Sn单调递减。由单调有界数列极限定理,可知Sn必有极限,因此
S=lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)存在。
于是设这个数为γ,这个数就叫作欧拉常数,他的近似值约为0.57721566490153286060651209,目前还不知道它是有理数还是无理数。在微积分学中,欧拉常数γ有许多应用,如求某些数列的极限,某些收敛数项级数的和等。例如求lim[1/(n+1)+1/(n+2)+…+1/(n+n)](n→∞),可以这样做:
lim[1/(n+1)+1/(n+2)+…+1/(n+n)](n→∞)=lim[1+1/2+1/3+…+1/(n+n)-ln(n+n)](n→∞)-lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)+lim[ln(n+n)-ln(n)](n→∞)=γ-γ+ln2=ln2
4 代码格式
using System;namespace Legalsoft.Truffer.Algorithm
{public static partial class Number_Sequence{private static double doubleFactorial(int n){if (n == 1) return 1;else return n * doubleFactorial(n - 1);}public static double Euler_Constant(int n){if (n == 0) return 1;else return (1 / doubleFactorial(n) + Euler_Constant(n - 1));}}
}相关文章:

C#,欧拉常数(Euler Constant)的算法与源代码
1 欧拉常数 欧拉常数最先由瑞士数学家莱昂哈德 欧拉 (Leonhard Euler) 在1735年发表的文章《De Progressionibus harmonicus observationes》中定义。欧拉曾经使用γ作为它的符号,并计算出了它的前6位,1761年他又将该值计算到了16位 。 欧拉常数最先由瑞…...

asio监听eventfd
c - Does BOOST asio supports eventfd? like epoll - Stack Overflow asio的官方example并没有asio监听eventfd的例子,但asio支持posix::stream_descriptor, 如果将eventfd包装成posix::stream_descriptor,并注册到io_context里…...

《统计学简易速速上手小册》第9章:统计学在现代科技中的应用(2024 最新版)
文章目录 9.1 统计学与大数据9.1.1 基础知识9.1.2 主要案例:社交媒体情感分析9.1.3 拓展案例 1:电商销售预测9.1.4 拓展案例 2:实时交通流量分析 9.2 统计学在机器学习和人工智能中的应用9.2.1 基础知识9.2.2 主要案例:预测客户流…...
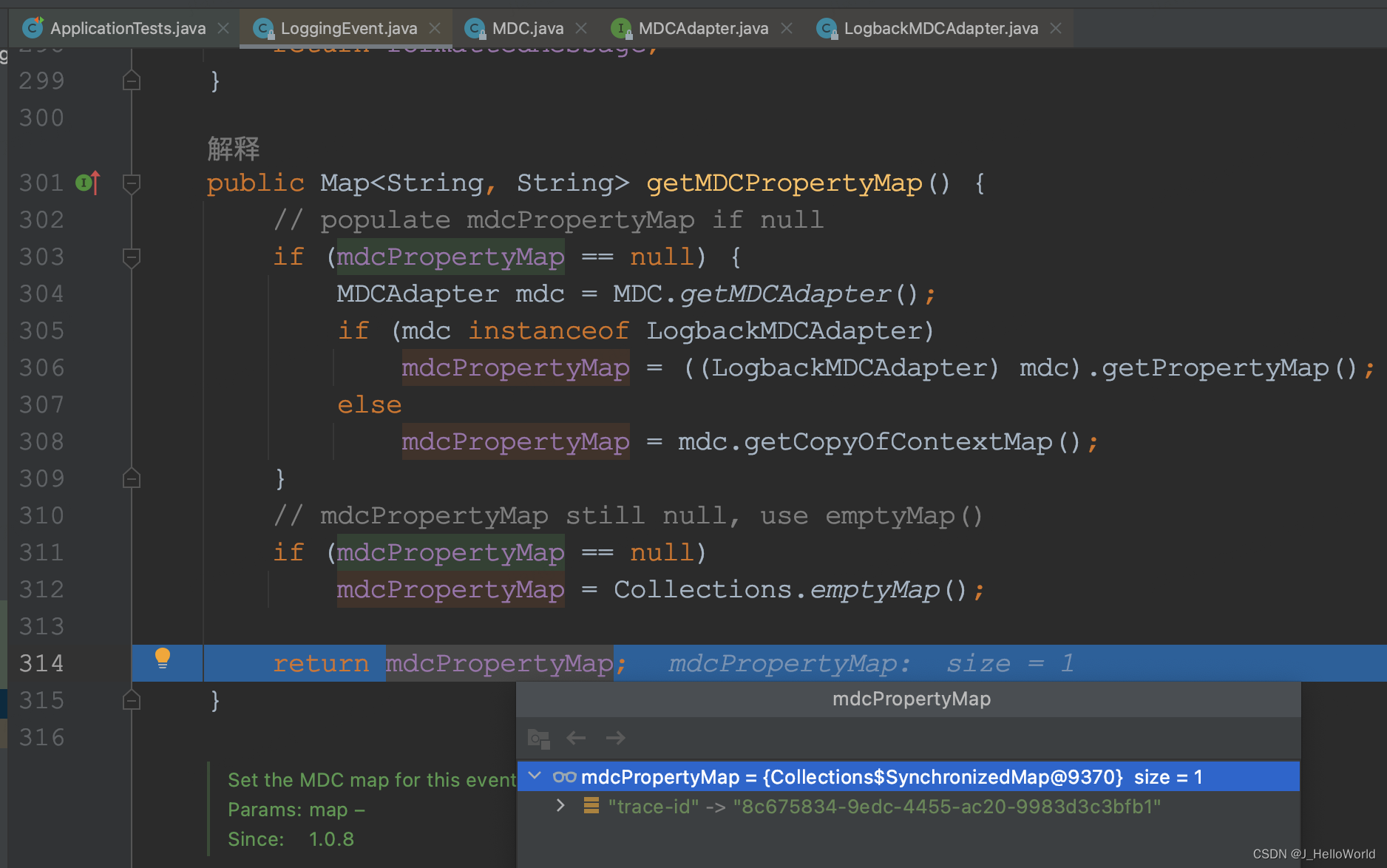
问题排查利器 - 分布式 trace
在分布式系统开发中,系统间的调用往往会横跨多个应用之间的接口。负责的调用链路也导致了,当线上环境出现问题时,例如请求失败、延迟增加或错误发生,我们无法第一时间确定是哪个环节出了问题,这给故障排查和修复带来了…...
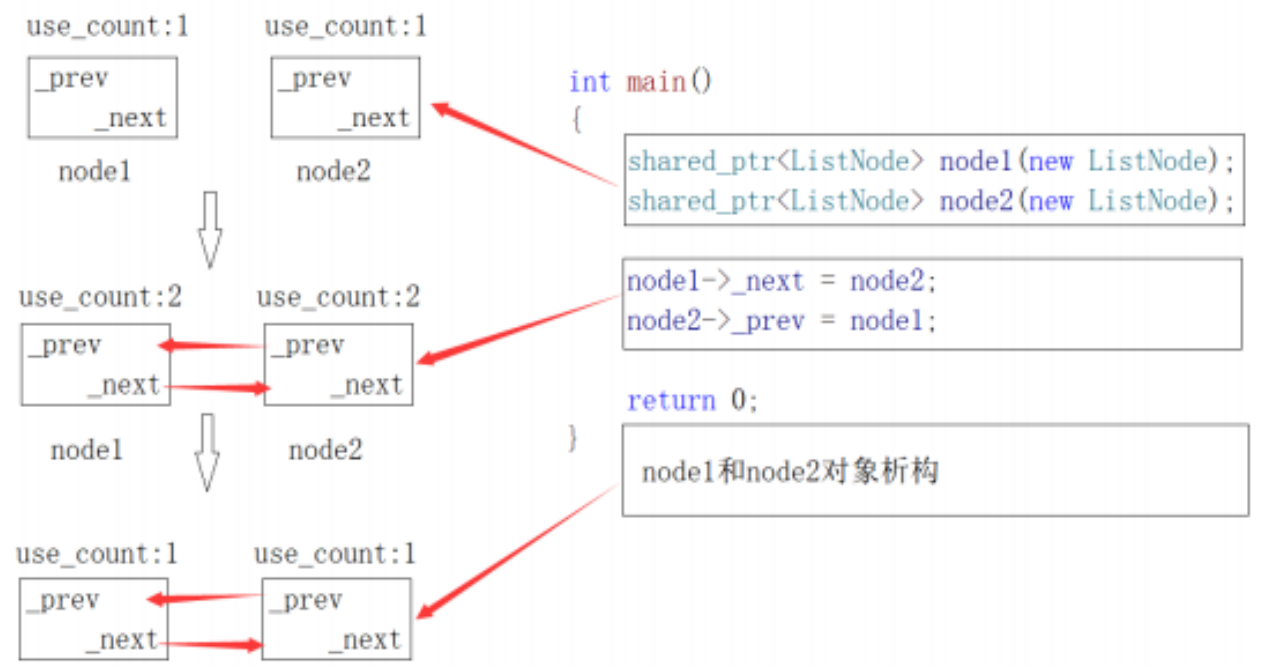
C++进阶(十四)智能指针
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、为什么需要智能指针?二、内存泄漏1、 什么是内存泄漏,内存泄漏的危…...

GPT最新进展:推出视频功能!迭代即将来临!
随着人工智能的不断进步,ChatGPT正准备以其全新的视频功能大跃进,同时,备受期待的GPT-5也即将在今年露面,预示着AI领域即将迎来一场变革。 在最近一期充满激情的Unconfuse Me播客中,OpenAI的首席执行官Sam Altman与技…...
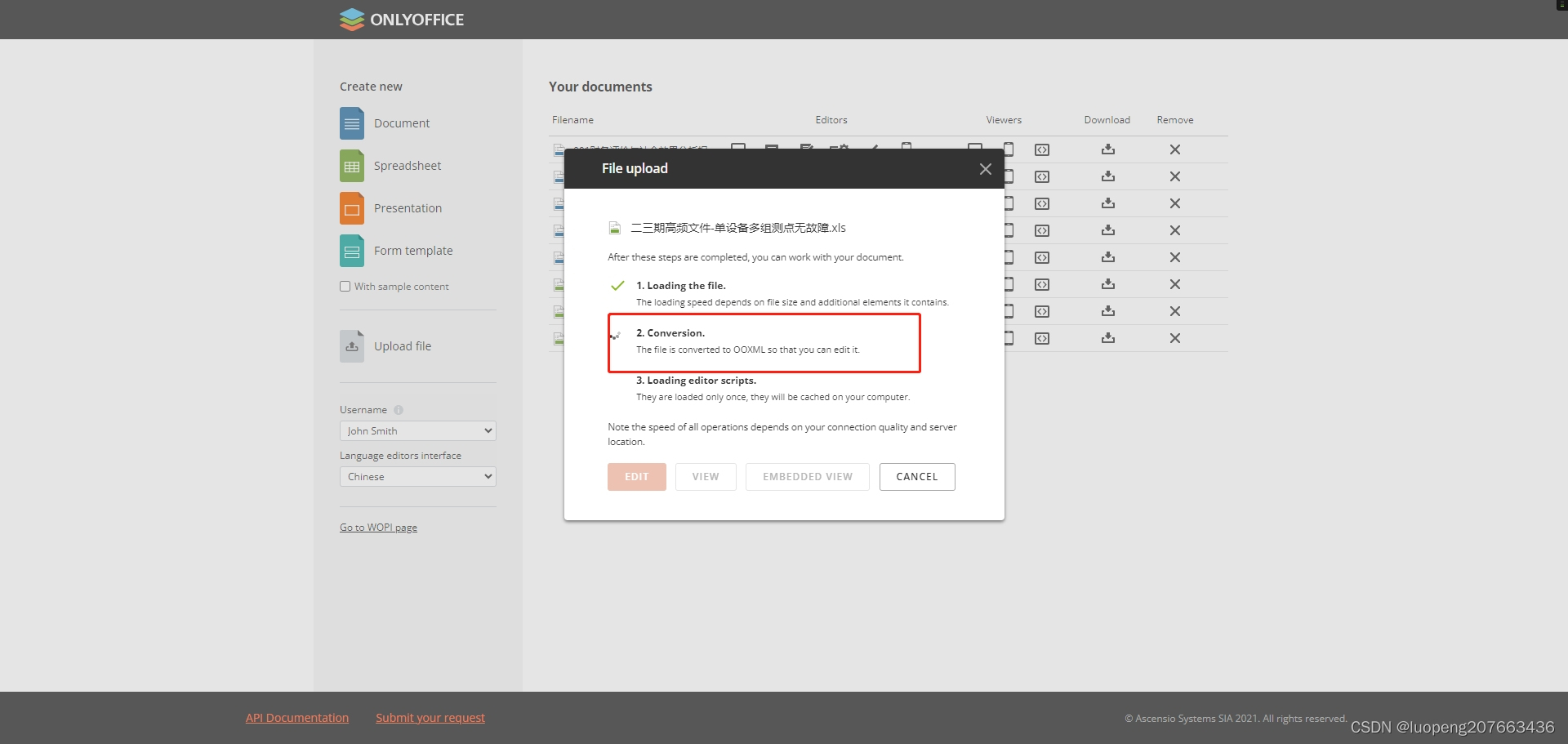
各款Excel、word在线预览工具对比分析以及onlyoffice预览Excel加载时间长的解决方案
对于onlyoffice插件预览慢的问题分析: 研究了一下onlyoffice,得出以下结论! 对于预览慢的问题,原因出在文件类型上,文件类型为低版本xls而非新版xlsx文件,onlyoffice服务器会自动将该文件转换为xlsx文件再…...

【课程作业_01】国科大2023模式识别与机器学习实践作业
国科大2023模式识别与机器学习实践作业 作业内容 从四类方法中选三类方法,从选定的每类方法中 ,各选一种具体的方法,从给定的数据集中选一 个数据集(MNIST,CIFAR-10,电信用户流失数据集 )对这…...

LeetCode374. Guess Number Higher or Lower——二分查找
文章目录 一、题目二、题解 一、题目 We are playing the Guess Game. The game is as follows: I pick a number from 1 to n. You have to guess which number I picked. Every time you guess wrong, I will tell you whether the number I picked is higher or lower th…...
继承
1.继承的作用 有些类与类之间存在特殊关系,下级别的成员除了拥有上一级别的共性,还有自己的特性。 这个时候我们就可以考虑利用继承技术,减少重复代码。 总结: 继承的好处:可以减少重复的代码 class A : public B;…...

北斗卫星在物联网时代的应用探索
北斗卫星在物联网时代的应用探索 在当今数字化时代,物联网的应用已经深入到人们的生活中的方方面面,让我们的生活更加智能便捷。而北斗卫星系统作为我国自主研发的卫星导航系统,正为物联网的发展提供了强有力的支撑和保障。本文将全面介绍北…...

SQL注入 - 利用报错函数 floor 带回回显
环境准备:构建完善的安全渗透测试环境:推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 一、原理 利用COUNT(), FLOOR(), RAND(), 和 GROUP BY来生成主键重复错误 函数解释 count(): 这个函数用于计算满足某一条件下的行数,是SQL中的一个聚合函数,常用于统计查询结…...
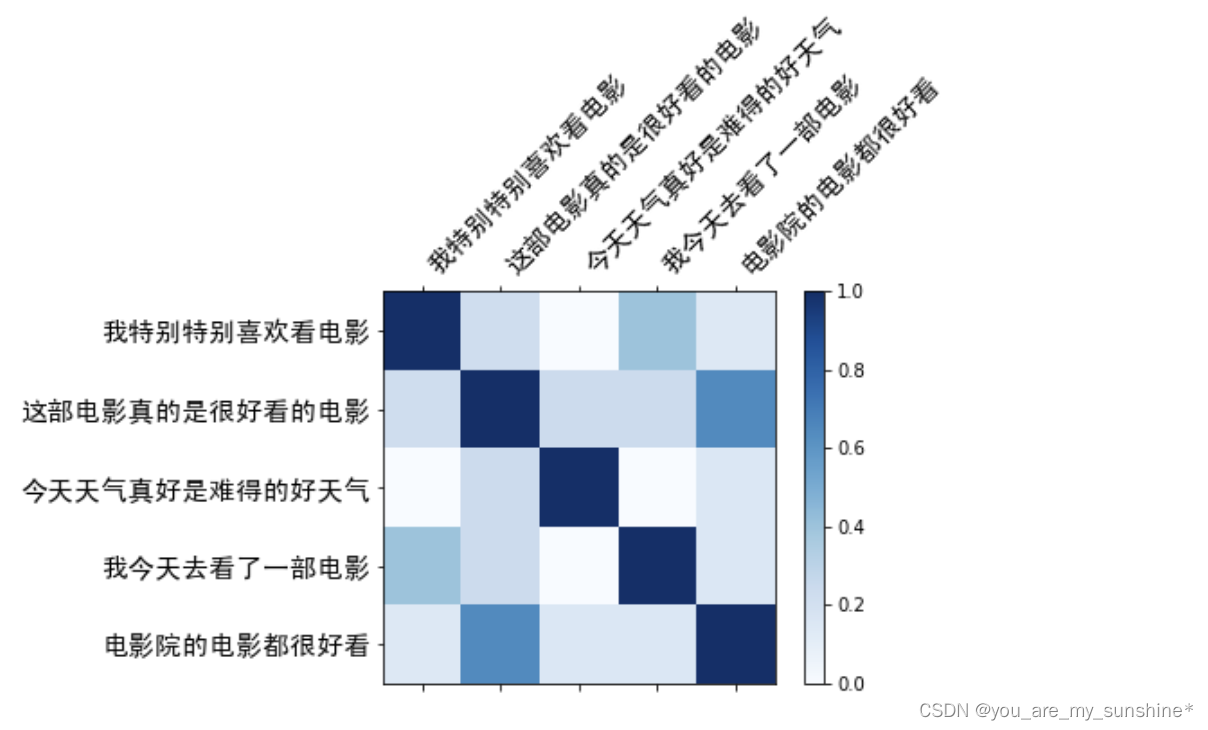
NLP_Bag-Of-Words(词袋模型)
文章目录 词袋模型用词袋模型计算文本相似度1.构建实验语料库2.给句子分词3.创建词汇表4.生成词袋表示5.计算余弦相似度6.可视化余弦相似度 词袋模型小结 词袋模型 词袋模型是一种简单的文本表示方法,也是自然语言处理的一个经典模型。它将文本中的词看作一个个独立…...
C语言rand随机数知识解析和猜数字小游戏
rand随机数 rand C语言中提供了一个可以随机生成一个随机数的函数:rand() 函数原型: int rand(void);rand函数返回的值的区间是:0~RAND_MAX(32767)之间。大部分编译器都是32767。 #include<stdlib.h> int ma…...

django中的缓存功能
一:介绍 Django中的缓存功能是一个重要的性能优化手段,它可以将某些耗时的操作(如数据库查询、复杂的计算等)的结果存储起来,以便在后续的请求中直接使用这些缓存的结果,而不是重新执行耗时的操作。Django…...
三、搜索与图论
DFS 排列数字 #include<iostream> using namespace std; const int N 10; int a[N], b[N]; int n;void dfs(int u){if(u > n){for(int i 1; i < n; i)cout<<a[i]<<" ";cout<<endl;return;}for(int i 1; i < n; i){if(!b[i]){b[…...
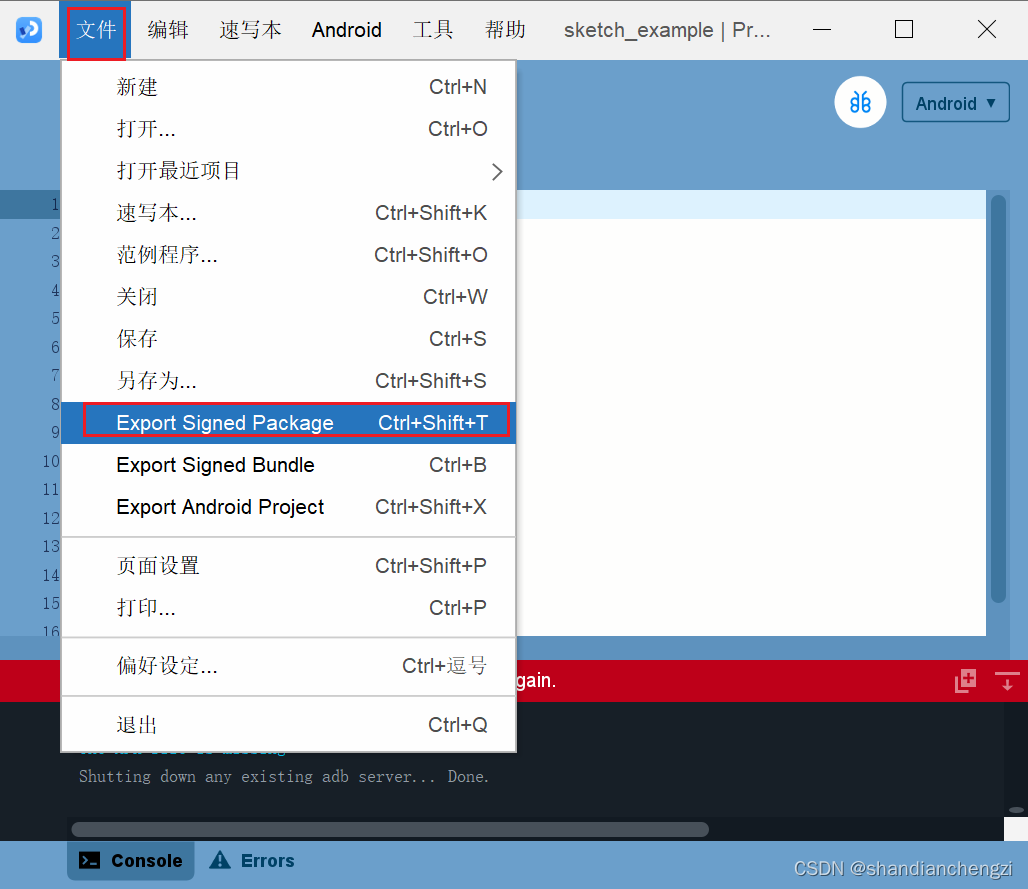
【翻译】Processing安卓模式的安装使用及打包发布(内含中文版截图)
原文链接在下面的每一章的最前面。 原文有三篇,译者不知道贴哪篇了,这篇干脆标了原创。。 译者声明:本文原文来自于GNU协议支持下的项目,具备开源二改授权,可翻译后公开。 文章目录 Install(安装࿰…...
MATLAB图像处理——边缘检测及图像分割算法
1.检测图像中的线段 clear clc Iimread(1.jpg);%读入图像 Irgb2gray(I); %转换为灰度图像 h1[-1, -1. -1; 2, 2, 2; -1, -1, -1]; %模板 h2[-1, -1, 2; -1, 2, -1; 2, -1, -1]; h3[-1, 2, -1; -1, 2, -1; -1, 2, -1]; h4[2, -1, -1; -1, 2, -1; -1, -1, 2]; J1imfilter(I, h1)…...

探索设计模式:原型模式深入解析
探索设计模式:原型模式深入解析 设计模式是软件开发中用于解决常见问题的标准解决方案。它们不仅能提高代码的可维护性和可复用性,还能让其他开发者更容易理解你的设计决策。今天,我们将聚焦于创建型模式之一的原型模式(Prototyp…...

IAR报错解决:Fatal Error[Pe1696]: cannot open source file “zcl_ha.h“
报错信息 Fatal Error[Pe1696]: cannot open source file "zcl_ha.h" K:\Z-Stack 3.0.2\Projects\zstack\Practice\SampleSwitch\Source\zcl_samplesw_data.c 51 意思是找不到zcl_ha.h文件 找不到的理由可能是我把例程复制了一份到别的文件目录下,少复制…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
