蓝桥杯每日一题------背包问题(二)
前言
本次讲解背包问题的一些延申问题,新的知识点主要涉及到二进制优化,单调队列优化DP,树形DP等。
多重背包

原始做法
多重背包的题意处在01背包和完全背包之间,因为对于每一个物品它规定了可选的个数,那么可以考虑将完全背包的第三维修改一下,j2表示选择的当前物品的个数,给它限制为s[i]。代码如下所示,
import java.util.Scanner;
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int k = scanner.nextInt();int[] v = new int[n + 1];int[] w = new int[n + 1];int[] s = new int[n + 1];for (int i = 1; i <= n; i++) {v[i] = scanner.nextInt();w[i] = scanner.nextInt();s[i] = scanner.nextInt();}int[][] dp = new int[n + 1][k + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j < k + 1; j++) {for (int j2 = 0; j2 * v[i] <= j && j2 <= s[i]; j2++) {dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - j2 * v[i]] + j2 * w[i]);
// dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - j2 * v[i]] + j2 * w[i]);//原本写的j2 = 1开始}}}System.out.println(dp[n][k]);}
}
这个的时间复杂度是 O ( N ∗ V ∗ S ) = 1000 ∗ 20000 ∗ 20000 = 4 e 11 O(N*V*S)=1000*20000*20000=4e11 O(N∗V∗S)=1000∗20000∗20000=4e11,时间复杂度太高需要优化。
二进制优化做法
假设最终的选择方案中,第i个物品需要选择p次,按照原始做法,这p次需要遍历p遍才能选出来,那么还有没有其它更快的做法?如果大家学过倍增或者快速幂学的较为深入的话,这里其实就是考虑快速算出数字p,我们很容易想到二进制,二进制可以表示十进制里的任何一个数字。比如p=10,写成二进制是1010,如果我们预处理过每个物品二进制的值,只需要执行4次就可以了,第一次遍历2的3次方,要选择。第二次遍历到2的2次方,不选择。第三次遍历2的1次方,要选择。第四次遍历2的0次方,不选择。
怎么预处理呢?假设s[i]是10,那么把2进制每一位表示的数字都处理出来,让它单独表示一个物品,比如1个物品i(s[i]个还剩9个),2个物品i(s[i]个还剩7个),4个物品i(s[i]个还剩3个),8个物品i(不够8个了,直接剩余的3个作为1组就行。这里为啥不能用8个?如果用了八个,在后续选择的过程中,我选了4个物品i和8个物品i这样就一共选了13个物品i,超出了它的最大可选值)。
预处理后我要怎么用呢?每一个看作单独的一个新物品,那么一个可选个数为S个的物品,可以被处理处logS(以2为底的S的对数)个新物品,那么S的最大值为20000,lon(20000)≈15。现在就变成了每个物品只能选择一个,可以使用01背包的代码,时间复杂度为 O ( N ∗ l o g S ∗ V ) = 1000 ∗ 15 ∗ 20000 = 3 e 8 O(N*logS*V)=1000*15*20000=3e8 O(N∗logS∗V)=1000∗15∗20000=3e8。时间复杂度比一开始好了很多,但是对于本题的数据规模还是不能通过。完整代码如下,
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;public class Main {static class good{int v,w;public good(int v, int w) {super();this.v = v;this.w = w;}}
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int V = scanner.nextInt();int[] v = new int[n+1];int[] w = new int[n+1];int[] s = new int[n+1];for (int i = 1; i < w.length; i++) {v[i] = scanner.nextInt();w[i] = scanner.nextInt();s[i] = scanner.nextInt();}//二进制预处理每一个物品List<good> list = new ArrayList<good>();list.add(new good(0,0));for (int i = 1; i < n+1; i++) {for (int j = 1; j <= s[i]; j *= 2) {list.add(new good(v[i]*j, w[i]*j));s[i] -= j;}if(s[i]>0) {list.add(new good(v[i]*s[i], w[i]*s[i]));}}//01背包代码int[][] dp = new int[list.size()][V+1];for (int i = 1; i < dp.length; i++) {for (int j = 0; j < V+1; j++) {dp[i][j] = Math.max(dp[i][j], dp[i-1][j]);if(j>=list.get(i).v)dp[i][j] = Math.max(dp[i][j], dp[i-1][j-list.get(i).v]+list.get(i).w);}}System.out.println(dp[list.size()-1][V]);
}
}单调队列优化做法
这个如果光看别人推导还是无法完全理解其中含义,还是需要自己进行推导。我们现在就开始进行推导,算法的本质其实和数学是有一定联系的,如果你光想百思不得其解,那么这个时候就该动笔了,动笔有两个方向,一个是自己推导,一个是根据它的推导结果进行模拟。
f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − v [ i ] ] + w [ i ] , f [ i − 1 ] [ j − 2 ∗ v [ i ] ] + 2 ∗ w [ i ] , f [ i − 1 ] [ j − 3 ∗ v [ i ] ] + 3 ∗ w [ i ] , f [ i − 1 ] [ j − 4 ∗ v [ i ] ] + 4 ∗ w [ i ] ) + . . . , f [ i − 1 ] [ j − t ∗ v [ i ] ] + t ∗ w [ i ] f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i],f[i-1][j-2*v[i]]+2*w[i],f[i-1][j-3*v[i]]+3*w[i],f[i-1][j-4*v[i]]+4*w[i])+...,f[i-1][j-t*v[i]]+t*w[i] f[i][j]=max(f[i−1][j],f[i−1][j−v[i]]+w[i],f[i−1][j−2∗v[i]]+2∗w[i],f[i−1][j−3∗v[i]]+3∗w[i],f[i−1][j−4∗v[i]]+4∗w[i])+...,f[i−1][j−t∗v[i]]+t∗w[i]
当i固定时,其中 j − t ∗ v [ i ] < v [ i ] j-t*v[i]<v[i] j−t∗v[i]<v[i],也就是 r = j − t ∗ v [ i ] r=j-t*v[i] r=j−t∗v[i]是j关于v[i]的余数。r可能的取值为 [ 0 , v [ i ] − 1 ] [0,v[i]-1] [0,v[i]−1],对于r来说,我们可以有下述公式,下述公式是上述公式倒推的结果。
f [ i ] [ r ] = f [ i − 1 ] [ r ] f[i][r]=f[i-1][r] f[i][r]=f[i−1][r]
f [ i ] [ r + v [ i ] ] = m a x ( f [ i − 1 ] [ r + v [ i ] ] , f [ i − 1 ] [ r ] ) f[i][r+v[i]]=max(f[i-1][r+v[i]],f[i-1][r]) f[i][r+v[i]]=max(f[i−1][r+v[i]],f[i−1][r])
f [ i ] [ r + 2 ∗ v [ i ] ] = m a x ( f [ i − 1 ] [ r + 2 ∗ v [ i ] , f [ i − 1 ] [ r + v [ i ] ] , f [ i − 1 ] [ r ] ) f[i][r+2*v[i]]=max(f[i-1][r+2*v[i],f[i-1][r+v[i]],f[i-1][r]) f[i][r+2∗v[i]]=max(f[i−1][r+2∗v[i],f[i−1][r+v[i]],f[i−1][r])
…
f [ i ] [ r + s [ i ] ∗ v [ i ] ] = m a x ( f [ i − 1 ] [ r + s [ i ] ∗ v [ i ] ] , f [ i − 1 ] [ r + ( s [ i ] − 1 ) ∗ v [ i ] ] . . . f [ i − 1 ] [ r ] ) f[i][r+s[i]*v[i]]=max(f[i-1][r+s[i]*v[i]],f[i-1][r+(s[i]-1)*v[i]]...f[i-1][r]) f[i][r+s[i]∗v[i]]=max(f[i−1][r+s[i]∗v[i]],f[i−1][r+(s[i]−1)∗v[i]]...f[i−1][r])
f [ i ] [ r + ( s [ i ] + 1 ) ∗ v [ i ] ] = m a x ( f [ i − 1 ] [ r + ( s [ i ] + 1 ) ∗ v [ i ] ] , f [ i − 1 ] [ r + s [ i ] ∗ v [ i ] ] . . . f [ i − 1 ] [ r + v [ i ] ] ) f[i][r+(s[i]+1)*v[i]]=max(f[i-1][r+(s[i]+1)*v[i]],f[i-1][r+s[i]*v[i]]...f[i-1][r+v[i]]) f[i][r+(s[i]+1)∗v[i]]=max(f[i−1][r+(s[i]+1)∗v[i]],f[i−1][r+s[i]∗v[i]]...f[i−1][r+v[i]])
对于第i个物品,最多只能选择s[i]个,一开始的体积是(s[i]+1)*v[i],体积变成r+v[i]时,已经选了s[i]个物品,后续不能再选择了。如果学过滑动窗口其实可以理解成窗口的大小为s[i]+1,这里的+1来源于不选择第i个物品,其余是依次选择1个,2个…s[i]个物品。
再接着向后写,最后一个是
f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − v [ i ] ] . . . f [ i − 1 ] [ j − s [ i ] ∗ v [ i ] ] ) f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]...f[i-1][j-s[i]*v[i]]) f[i][j]=max(f[i−1][j],f[i−1][j−v[i]]...f[i−1][j−s[i]∗v[i]])
f[i][j]等于对大小为s[i]+1的窗口取最大值,用单调队列去维护,这里只需要O(1)的时间复杂度,那么对于第1维度当前考虑前i个物品,不能省略,和以前一样。对于第2个维度,体积,这里只需要遍历j对于v[i]的余数r即可,然后再来一个for循环,遍历当前的体积,但是他是在r的基础上累加v[i]直到大于总体积j,那么虽然这里是两个for循环遍历的体积,但是总的次数依然是从体积的次数,只不过改变了遍历的顺序,先遍历对v[i]取模余0的体积大小,再遍历对v[i]取模余1的体积大小,依次类推。看一下这里的代码,
for(int i = 1;i <= N;i++) {for(int r = 0;r < v[i];r++) {for(int j = r;j <= M;j += v[i]) {}}}
所以这个思路的时间复杂度是 O ( N ∗ V ) = 1000 ∗ 20000 = 2 e 7 O(N*V)=1000*20000=2e7 O(N∗V)=1000∗20000=2e7,此时的时间复杂度就符合要求。本题的关键在于理解上述for循环,理解这里后面就是顺理成章的事情。
接下来考虑单调队列实现滑动窗口。这里简单介绍一下滑动窗口,假设有一个长度为10的数组,滑动窗口的大小是3,求滑动窗口里的最大值,其过程如下,
从数组下标为1初开始遍历,依次向队列里面添加元素。
第一个while循环把此时不在窗口内的数字从队列里面删除。
假设此时在队列里面的数组下标分别为1,2,3,4。队尾元素减队头元素+1就是此时队列里的元素个数(注意这里存的是数组对应的下标),如果大于3,需要将队头元素移除(因为对头元素是最早进入队列的,比如这个例子里就要把数字1移除)。重复上述过程,直到队列里面的元素个数等于3。
但是对于本题而言,所谓的下标表示的是此时的体积,只要体积之差不超过s[i]*v[i]即可,注意这里的灵活变通,代码如下,
while(!queue.isEmpty()&&j-queue.peekFirst()>s[i]*v[i]) queue.pollFirst();
第二个while循环把后续不会对答案构成贡献的数字提前删掉。当前维护的是窗口里的最大值,那么对于队列而言,队头元素维护的就是最大值,整个队列从队头到队尾是单调递减序列。那么如果新加入的元素是要放在队尾的,如果它比此时队尾的元素大,就要删除队尾的元素,重复执行,直到它比队尾的元素小,或者队列为空。(原因:假设队列里此时有2,3,4,此时要加入5,a[5]>a[4],也就是说如果窗口内同时存在a[4]和a[5],a[5]会是最大值,也就是只要有a[5]存在a[4]永远不会成为最大值,而随着窗口的移动,a[4]会先被移走,所以只要a[4]在,a[5]一定在,那么a[4]不会对答案产生贡献,直接删除不会造成影响)
注意对于本题而言,对应的值应该加上这几个物品的价值,代码如下,
while(!queue.isEmpty()&&dp[i-1][queue.peekLast()]+(j-queue.peekLast())/v[i]*w[i]<=dp[i-1][j]) queue.pollLast();
( j − q u e u e . p e e k L a s t ( ) ) / v [ i ] (j-queue.peekLast())/v[i] (j−queue.peekLast())/v[i]表示对于体积为j时,选择的第i个物品的个数。
while结束后,把当前值插入队列,这里插入的是dp[i-1][j],但是队列里面只记录j,所以插入的是j,然后把队列的最大值赋值给dp[i][j]。代码如下,
queue.add(j);
dp[i][j] = dp[i-1][queue.peekFirst()]+(j-queue.peekFirst())/v[i]*w[i];
注意对于每一个物品队列是不同的,所以要有清空队列的操作,完整代码如下,
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.Scanner;public class Main{
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int N = scanner.nextInt();int M = scanner.nextInt();int v[] = new int[N+1];int w[] = new int[N+1];int s[] = new int[N+1];for(int i = 1;i <= N;i++) {v[i] = scanner.nextInt();w[i] = scanner.nextInt();s[i] = scanner.nextInt();}int dp[][] = new int[N+1][M+1];ArrayDeque<Integer> queue = new ArrayDeque<Integer>();for(int i = 1;i <= N;i++) {for(int r = 0;r < v[i];r++) {queue.clear();for(int j = r;j <= M;j += v[i]) {while(!queue.isEmpty()&&j-queue.peekFirst()>s[i]*v[i]) queue.pollFirst();while(!queue.isEmpty()&&dp[i-1][queue.peekLast()]+(j-queue.peekLast())/v[i]*w[i]<=dp[i-1][j]) queue.pollLast();queue.add(j);dp[i][j] = dp[i-1][queue.peekFirst()]+(j-queue.peekFirst())/v[i]*w[i];}}}System.out.println(dp[N][M]);
}
}多重背包就讲完了,主要讲了两种优化方法来应对数据规模较大的情况。
混合背包

混合背包就是01背包、完全背包、多重背包的结合体,其实完全可以变成多重背包,因为多重背包的s[i]=1时就是01背包,s[i]=∞(用一个比较大的数)时就是完全背包,话不多说,直接看代码吧,这里用的最普通的代码,
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int k = scanner.nextInt();int[] v = new int[n + 1];int[] w = new int[n + 1];int[] s = new int[n + 1];for (int i = 1; i <= n; i++) {v[i] = scanner.nextInt();w[i] = scanner.nextInt();s[i] = scanner.nextInt();if (s[i] == -1) {s[i] = 1;}if (s[i] == 0) {s[i] = 1000000000;}}int[][] dp = new int[n + 1][k + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j < k + 1; j++) {for (int j2 = 0; j2 * v[i] <= j && j2 <= s[i]; j2++) {dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - j2 * v[i]] + j2 * w[i]);
// dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - j2 * v[i]] + j2 * w[i]);//原本写的j2 = 1开始,可是这样不对}}}System.out.println(dp[n][k]);}
}二维费用的背包问题

类似01背包,只是多了一个维度,那么这里再用之前介绍的动态规划思路来思考一下。
第一步:缩小规模。考虑n个物品,那我就先考虑1个物品,再考虑2个物品…,需要一个维度表示当前考虑的物品个数。
第二步:限制。
(1)所选物品个数不能超过背包容量,那么需要一个维度记录当前背包的容量。
(2)所选物品个数不能超过背包重量,那么需要一个维度记录当前背包的重量。
第三步:写出dp数组。dp[i][j][k]表示当前考虑了前i个物品,背包容量为j,重量为k时的最大价值。
第四步:推状态转移方程。dp[i][j][k]应该从哪里转移过来呢,必然是从前i-1个物品转移,我要考虑两种情况,对于第i个物品,可以选择要它,也可以不要它,如果要第i个物品,我就需要背包里面给我预留出第i个物品的体积和重量,也就是从a[i-1][j-v[i]][k-m[i]]转移,同时也能获得该物品的价值。如果不要第i个物品,那么之前从前一个状态相同容量的背包转移过来就行,即a[i-1][j][k]。
综上状态转移方程如下
a [ i ] [ j ] = m a x ( a [ i − 1 ] [ j ] [ k ] , a [ i − 1 ] [ j − v [ i ] ] [ k − m [ i ] ] + w [ i ] ) a[i][j] = max(a[i-1][j][k],a[i-1][j-v[i]][k-m[i]]+w[i]) a[i][j]=max(a[i−1][j][k],a[i−1][j−v[i]][k−m[i]]+w[i])
考虑写代码了
第一步:确定好遍历顺序,对于背包问题,一般第一个for遍历规模,第二个for遍历限制,但是我们有两个限制所以需要两个嵌套的for循环分别表示容量和重量。
代码如下,
import java.util.Scanner;
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int k = scanner.nextInt();//容积int mm = scanner.nextInt();//重量int[] v = new int[n+1];//容积int[] w = new int[n+1];int[] m = new int[n+1];//重量for (int i = 1; i < n+1; i++) {v[i] = scanner.nextInt();//容积m[i] = scanner.nextInt();//重量w[i] = scanner.nextInt();}int[][][] dp = new int[n+1][k + 1][mm + 1];for (int j = 1; j <= n; j++) {for (int i = 1; i <= k; i++) {for (int q = 1; q <= mm; q++){dp[j][i][q] = dp[j-1][i][q];if(i>=v[j]&&q>=m[j])dp[j][i][q] = Math.max(dp[j][i][q], dp[j-1][i - v[j]][q - m[j]] + w[j]);}}}//for (int i = 1; i < dp.length; i++) {//}System.out.println(dp[n][k][mm]);}
}
分组背包问题

分组背包的关键在于每一组的物品只能选一个,这个要求我们只需要在选物品的时候来进行约束即可,因此dp数组的含义还是和原来一样的。本来是每个物品遍历一次取一个最大值,现在是遍历某一组的物品,选取一个最大值。其实对于完全背包而言,遍历选择多个物品的情况,然后在其中选一个最大值也相当于一个分组,直接看代码吧,
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {static class good{int v,w;public good(int v, int w) {super();this.v = v;this.w = w;} }
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int V = scanner.nextInt();List<good> goods[] = new ArrayList[n+1];for (int i = 1; i < goods.length; i++) {goods[i] = new ArrayList<good>();int m = scanner.nextInt();for (int j = 0; j < m; j++) {goods[i].add(new good(scanner.nextInt(), scanner.nextInt()));}}int[][] dp = new int[n+1][V+1];for (int i = 1; i < dp.length; i++) {for (int k = 0; k < V+1; k++) {dp[i][k] = dp[i-1][k];for (int j = 0; j < goods[i].size(); j++) {if(goods[i].get(j).v<=k)dp[i][k] = Math.max(dp[i][k], dp[i-1][k-goods[i].get(j).v]+goods[i].get(j).w);}} }System.out.println(dp[n][V]);
}
}
简要分析一下代码,用good去存每一个分组,good[i]存的是第i个分组的物品。
遍历的时候先遍历分组,再遍历背包容量,然后遍历当前分组可以使用的物品,取一个最大值。
有依赖的背包问题
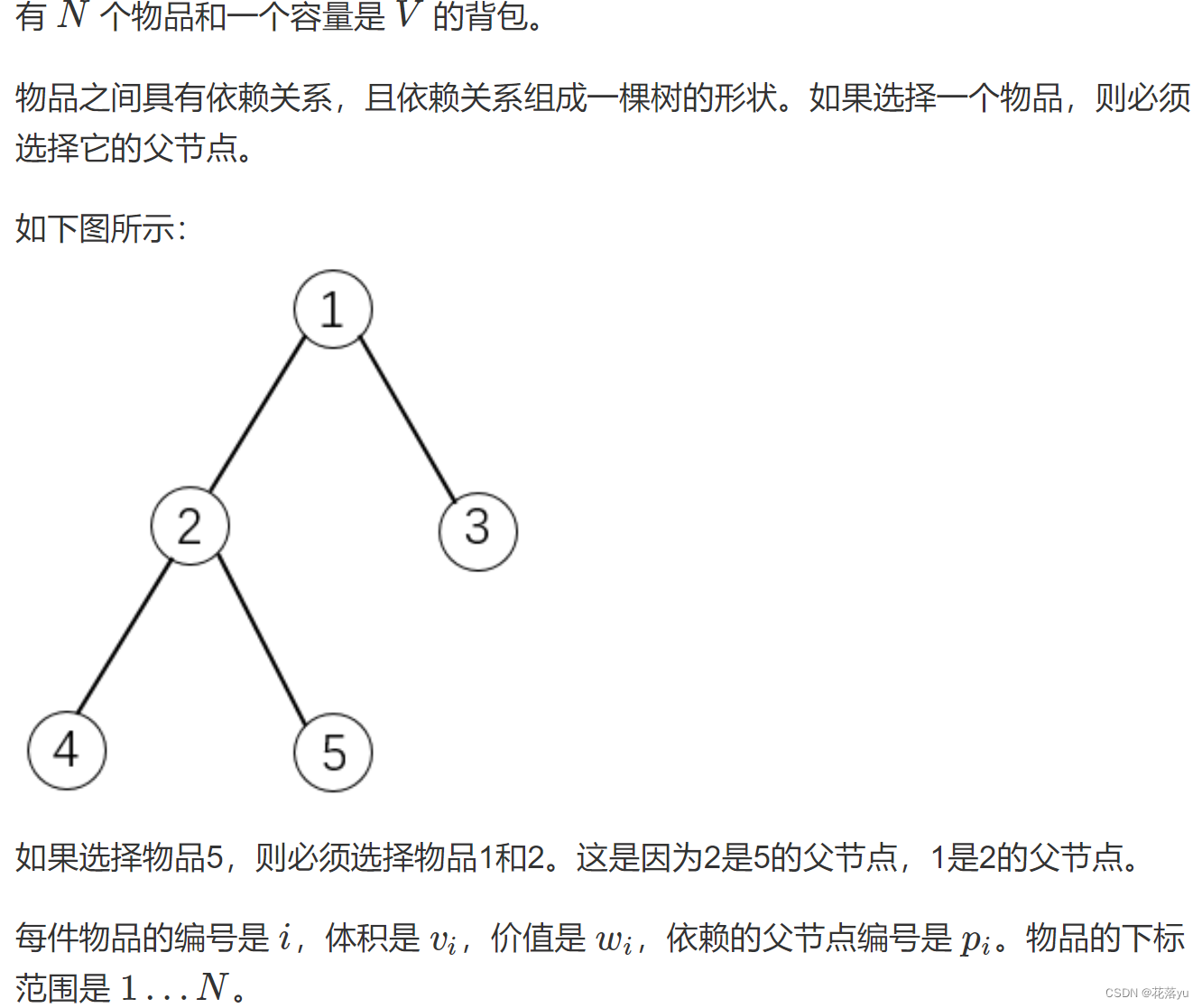

保证所有物品构成一颗树,如果选择了儿子节点,父节点必须选择。这里其实有一点像树形dp了,树形dp的dp数组定义套路和背包dp不太一样。
定义dp数组
第一步:缩小规模。这里考虑的是一棵树,考虑以root节点为根节点的树,然后root节点有son节点,为了缩小规模,接着考虑以son节点为根节点的树。
第二步:限制。所选物品个数不能超过物品容量,那么需要一个维度记录当前背包的容量。
第三步:写出dp数组。dp[i][j]表示当前考虑了以节点i为根节点的子树所具有的物品,背包容量为j时的最大价值。
第四步:推状态转移方程。dp[i][j]应该从哪里转移过来呢,必然是从i的儿子节点son转移过来。对于son来说他有多个不同的状态dp[son][k],在转移的时候j需要遍历,k也需要遍历,所以有两层嵌套的for循环。
为了满足这个条件,我们从根节点开始遍历,一般这种遍历就需要dfs了,从根节点进入就是dfs(root),dfs(root)返回的是以root为根的子树的最大值,也就是物品考虑了以root为父节点的所有物品可以选出来的最大值。
然后遍历root的所有儿子节点,这里用的链式前向星存储节点,其实对于java而言,用list或者hashmap存节点都可以。
for (int i = h[u]; i != -1 ; i = ne[i]) {int son = e[i];}}
对于以儿子节点为根的所有物品,我有选择和不选两种操作,但是如果我要选择儿子节点,我一定要选择父节点,所以在选择儿子节点时我要预留出父节点的位置。所以下面代码是从m-v[u]开始的,减掉的是给父节点预留的,第一个for循环遍历的是以父节点为根的物品在不同的背包容量下的结果,第二个for循环遍历的是以儿子节点为根的物品在不同的背包容量下的结果。
for (int j = m - v[u]; j >= 0; j--) {//u节点的所有可能的重量的组合for (int k = 0; k <= j; k++) {//u节点的子节点可以选的重量的组合dp[u][j] = Math.max(dp[u][j], dp[u][j-k]+dp[son][k]);} }
在进行这个操作之前,以儿子节点为根的物品在不同的背包容量下的结果应该已经求出来了。所以在for循环之前有dfs(son)。
所有儿子节点都考虑完了之后,把当前父节点加进去。
for (int i = m; i >= v[u]; i--) {dp[u][i] = dp[u][i-v[u]] + w[u];}for (int i = 0; i < v[u]; i++) {dp[u][i] = 0;}
全部代码如下,
import java.util.Arrays;
import java.util.Scanner;public class Main{static int[] h;static int[] ne;static int[] e;static int idx;static int dp[][];static int[] w;static int[] v;static int n;static int m;
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();m = scanner.nextInt();w = new int[n+1];//价值v = new int[n+1];//体积h = new int[n+1];ne = new int[n+1];Arrays.fill(h, -1);e = new int[n+1];dp = new int[n+1][m+1];int s;int root = -1;for (int i = 1; i < n+1; i++) {v[i] = scanner.nextInt();w[i] = scanner.nextInt();s = scanner.nextInt();if(s == -1) {root = i;}else {add(s,i);}}dfs(root);System.out.println(dp[root][m]);
}
private static void dfs(int u) {for (int i = h[u]; i != -1 ; i = ne[i]) {int son = e[i];dfs(son);for (int j = m - v[u]; j >= 0; j--) {//u节点的所有可能的重量的组合for (int k = 0; k <= j; k++) {//u节点的子节点可以选的重量的组合dp[u][j] = Math.max(dp[u][j], dp[u][j-k]+dp[son][k]);} }}for (int i = m; i >= v[u]; i--) {dp[u][i] = dp[u][i-v[u]] + w[u];}for (int i = 0; i < v[u]; i++) {dp[u][i] = 0;}
}
private static void add(int a, int b) {// TODO Auto-generated method stube[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
}
这里我们要明确一点,就是如果当前背包容量可以让我们选儿子节点,那么就是不选白不选,区别在于不能选全部儿子节点时要选哪一个儿子节点。
相关文章:

蓝桥杯每日一题------背包问题(二)
前言 本次讲解背包问题的一些延申问题,新的知识点主要涉及到二进制优化,单调队列优化DP,树形DP等。 多重背包 原始做法 多重背包的题意处在01背包和完全背包之间,因为对于每一个物品它规定了可选的个数,那么可以考虑…...

牛客错题整理——C语言(实时更新)
1.以下程序的运行结果是() #include <stdio.h> int main() { int sum, pad,pAd; sum pad 5; pAd sum, pAd, pad; printf("%d\n",pAd); }答案为7 由于赋值运算符的优先级高于逗号表达式,因此pAd sum, pAd, pad;等价于(…...

CIFAR-10数据集详析:使用卷积神经网络训练图像分类模型
1.数据集介绍 CIFAR-10 数据集由 10 个类的 60000 张 32x32 彩色图像组成,每类 6000 张图像。有 50000 张训练图像和 10000 张测试图像。 数据集分为5个训练批次和1个测试批次,每个批次有10000张图像。测试批次正好包含从每个类中随机选择的 1000 张图像…...

《傲剑狂刀》中的人物性格——龙吟风
在《傲剑狂刀》这款经典武侠题材的格斗游戏中,龙吟风作为一位具有传奇色彩的角色,其性格特征复杂且引人入胜。以下是对龙吟风这一角色的性格特点进行深度剖析: 一、孤高独立的剑客气质 龙吟风的名字本身就流露出一种独特的江湖气息,"吟风"象征着他的飘逸与淡泊名…...
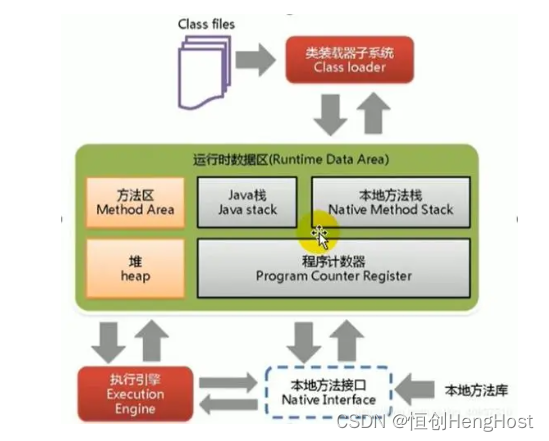
KVM和JVM的虚拟化技术有何区别?
随着虚拟化技术的不断发展,KVM和JVM已成为两种主流的虚拟化技术。尽管它们都提供了虚拟化的解决方案,但它们在实现方式、功能和性能方面存在一些重要的差异。本文将深入探讨KVM和JVM的虚拟化技术之间的区别。 KVM(Kernel-based Virtual Mac…...
 持续更新中)
LeetCode力扣 面试经典150题 详细题解 (1~5) 持续更新中
目录 1.合并两个有序数组 2.移动元素 3.删除有序数组中的重复项 4.删除排序数组中的重复项 II 5.多数元素 暂时更新到这里,博主会持续更新的 1.合并两个有序数组 题目(难度:简单): 给你两个按 非递减顺序 排列的…...

如何解决利用cron定时任务自动更新SSL证书后Nginx重启问题
利用cron定时任务自动更新SSL证书后,用浏览器访问网站,获取到的证书仍然是之前的。原因在于没有对Nginx进行重启。 据说certbot更新完成证书后会自动重启Nginx,但显然经我检测不是这回事儿。 所以我们需要创建一bash脚本,然后定时调用这个脚…...
第一个 Angular 项目 - 静态页面
第一个 Angular 项目 - 静态页面 之前的笔记: [Angular 基础] - Angular 渲染过程 & 组件的创建 [Angular 基础] - 数据绑定(databinding) [Angular 基础] - 指令(directives) 这是在学完了上面这三个内容后能够完成的项目,目前因为还没有学到数…...
网络协议与攻击模拟_17HTTPS 协议
HTTPShttpssl/tls 1、加密算法 2、PKI(公钥基础设施) 3、证书 4、部署HTTPS服务器 部署CA证书服务器 5、分析HTTPS流量 分析TLS的交互过程 一、HTTPS协议 在http的通道上增加了安全性,传输过程通过加密和身份认证来确保传输安全性 1、TLS …...
【linux系统体验】-ubuntu简易折腾
ubuntu 一、终端美化二、桌面美化2.1 插件安装2.2 主题和图标2.3 美化配置 三、常用命令 以后看不看不重要,咱就是想记点儿东西。一、终端美化 安装oh my posh,参考链接:Linux 终端美化 1、安装字体 oh my posh美化工具可以使用合适的字体&a…...

Android 判断通知是进度条通知
1.需求: 应用监听安卓系统中的通知,需要区分出带进度条的通知. 当使用NotificationCompat.Builder构建一个通知时,可以通过调用setProgress(max, progress, indeterminate)方法来添加一个进度条。这里的max参数表示最大进度值,progress表示当前进度值&a…...

学习数据结构和算法的第8天
顺序表的实现 顺序表 本质就是数组 概念及结构 顺序表是用一段物理地址连续的储存单元依次储存数据元素的线性结构,一般情况下采用数组储存,在数组上完成数据的增删。 顺序表就是数组,但是在数组的基础上,它还要求数据…...
JCIM | MD揭示PTP1B磷酸酶激活RtcB连接酶的机制
Background 内质网应激反应(UPR) 中的一个重要过程。UPR是由内质网中的三种跨膜传感器(IRE1、PERK和ATF6)控制的细胞应激反应,当内质网中的蛋白质折叠能力受到压力时,UPR通过减少蛋白质合成和增加未折叠或错…...

基于Java (spring-boot)的音乐管理系统
一、项目介绍 播放器的前端: 1.首页:点击歌单中的音乐播放列表中的歌曲进行播放,播放时跳转播放界面,并显示歌手信息,同时会匹配歌词,把相应的歌词显示在歌词面板中。 2.暂停:当歌曲正在播放时…...

在 MacOS M系列处理器上使用 Anaconda 开发 Oralce 的Python程序
在 MacOS M系列处理器上使用 Anaconda 开发 Oralce 的Python程序 因oracle官方驱动暂无 苹果 M 系列处理器版本,所以使用Arm的python解释器报驱动错误: cx_Oracle.DatabaseError: DPI-1047: Cannot locate a 64-bit Oracle Client library: "dlop…...

四、OpenAI之文本生成模型
文本生成模型 OpenAI的文本生成模型(也叫做生成预训练的转换器(Generative pre-trained transformers)或大语言模型)已经被训练成可以理解自然语言、代码和图片的模型。模型提供文本的输出作为输入的响应。对这些模型的输入内容也被称作“提示词”。设计提示词的本质是你如何对…...

CSS之flex布局
flex布局 CSS的Flex布局(Flexible Box Layout)是一种用于在页面上布置元素的高效方法,特别适合于响应式设计。Flex布局使得元素能够伸缩以适应可用空间,可以简化很多原本需要复杂CSS和HTML结构才能实现的布局设计。 flex布局包括…...

UnityShader——02三大主流编程语言
三大主流编程语言 Shader Language Shader language的发展方向是设计出在便携性方面可以与C/JAVA相比的高级语言,“赋予程序员灵活而方便的编程方式”,并“利用图形硬件的并行性,提高算法的效率” Shader language目前主要有 3 种语言&…...
Centos7安装nginx yum报错
Centos7安装nginx yum报错,yum源报错解决办法: 1、更新epel源后,出现yum报错 [roothacker117 ~]# yum install epel-release(安装成功) [roothacker117 ~]# yum install nginx(安装失败,提示如…...

【机组】基于FPGA的32位算术逻辑运算单元的设计(EP2C5扩充选配类)
🌈个人主页:Sarapines Programmer🔥 系列专栏:《机组 | 模块单元实验》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 一、实验目的 二、实验要求 …...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
