LeetCode--代码详解 155.最小栈
155.最小栈
题目
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
示例 1:
输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]]输出: [null,null,null,null,-3,null,0,-2]解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
提示:
-231 <= val <= 231 - 1pop、top和getMin操作总是在 非空栈 上调用push,pop,top, andgetMin最多被调用3 * 104次
思路
用栈存储正常的值,再用一个栈从大到小存储最小值
代码
class MinStack {private Stack<Integer> stack;private Stack<Integer> minStack;public MinStack() {this.stack = new Stack<>();this.minStack = new Stack<>();}public void push(int val) {stack.push(val);if (!minStack.isEmpty()) {int top = minStack.peek();if (top >= val) minStack.push(val);} else minStack.push(val);}public void pop() {int pop = stack.pop();int top = minStack.peek();if (pop == top) minStack.pop();}public int top() {return stack.peek();}public int getMin() {return minStack.peek();}
}相关文章:

LeetCode--代码详解 155.最小栈
155.最小栈 题目 设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶…...

第6讲后端鉴权拦截器实现
后端鉴权拦截器实现 package com.java1234.interceptor;import com.java1234.util.JwtUtils; import com.java1234.util.StringUtil; import io.jsonwebtoken.Claims; import org.springframework.web.method.HandlerMethod; import org.springframework.web.servlet.HandlerI…...

uniapp从入门到进阶
一、了解uniapp 跨平台开发:Uniapp可以同时开发多个平台的应用,只需编写一套代码即可。开发者可以通过编写Vue组件来构建界面,通过编写JavaScript代码来实现业务逻辑。 页面和组件:Uniapp的页面和组件都是基于Vue组件的ÿ…...

CDN缓存404、403状态码
可以参考一下:浏览器缓存和 CDN 在前端的落地 事故记录: 前端发版时存在新旧两个容器,在资源替换的间隙,用户请求到的肯定是新容器的html文件,但是根据新容器的html向新静态资源发起请求,此时旧容器还没有…...

【Python网络编程之DHCP服务器】
🚀 作者 :“码上有前” 🚀 文章简介 :Python开发技术 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 Python网络编程之DHCP服务器 代码见资源,效果图如下一、实验要求二、协议原理2.1 D…...

【MySQL】:深入理解并掌握DML和DCL
🎥 屿小夏 : 个人主页 🔥个人专栏 : MySQL从入门到进阶 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一. DML1.1 添加数据1.2 修改数据1.3 删除数据 二. DCL2.1 管理用户2.2 权限控制…...
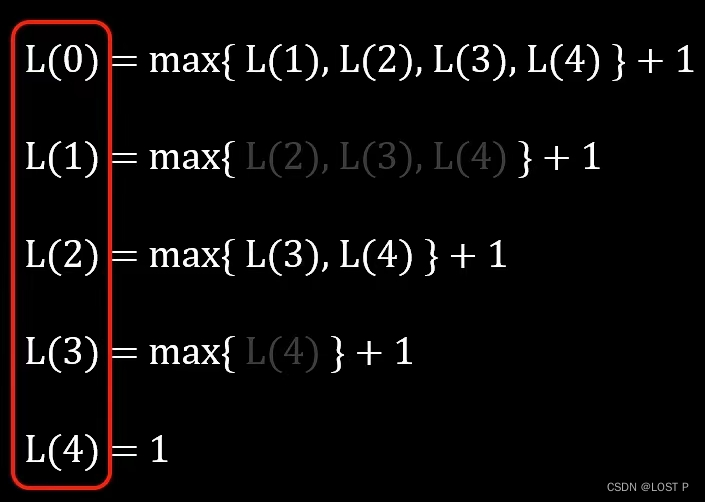
CSP-动态规划-最长公共子序列(LCS)
一、动态规划 动态规划(Dynamic Programming,简称DP)主要用于求解可以被分解为相似子问题的复杂问题,特别是在优化问题上表现出色,如最短路径、最大子数组和、编辑距离等。动态规划的核心思想是将原问题分解为较小的子…...

安装nodejs2011并配置npm仓库
1. 安装nodejs 选择2011版本下载 在安装目录(个人情况)下 D:\Program Files\nodejs2011创建2个文件夹: node_global (依赖库) node_cache (缓存) 然后在当前目录下cmd进入dos窗口,执行: npm c…...
)
排序C++代码(已更:快速排序,归并排序)
一、快速排序 #include<iostream> using namespace std;//设定三个数组,判断排序算法代码的正确性 int a[100]{3,4,2,6,9,7,1,0,1,2,3,3,5,6,7,8,3,4,5}; int b[100]{1,5,3,4}; int c[100]{7,8,9,1,2,3};void quickSort(int* num,int l,int r){if(l>r) re…...

CentOS 7.9安装Tesla M4驱动、CUDA和cuDNN
正文共:1333 字 21 图,预估阅读时间:2 分钟 上次我们在Windows上尝试用Tesla M4配置深度学习环境(TensorFlow识别GPU难道就这么难吗?还是我的GPU有问题?),但是失败了。考虑到Windows…...

Java设计模式——策略
前言 策略模式是平时Java开发中常用的一种,虽然已有很多讲解设计模式的文章,但是这里还是写篇文章来从自己理解的角度讲解一下。 使用场景 我们不妨进行场景假设,要对我们的软件进行授权管理:在启动我们的软件之前先要校验是否…...
线性代数的本质 1 向量
向量是线性代数中最为基础的概念。 何为向量? 从物理上看, 向量就是既有大小又有方向的量,只要这两者一定,就可以在空间中随便移动。 从计算机应用的角度看,向量和列表很接近,可以用来描述某对象的几个不同…...

基于JAVA的贫困地区人口信息管理系统 开源项目
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 人口信息管理模块2.2 精准扶贫管理模块2.3 特殊群体管理模块2.4 案件信息管理模块2.5 物资补助模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 人口表3.2.2 扶贫表3.2.3 特殊群体表3.2.4 案件表3.2.5 物资补助表 四…...
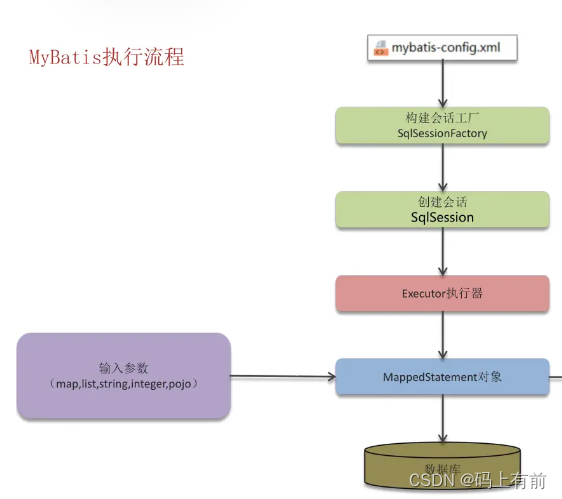
【后端高频面试题--Mybatis篇】
🚀 作者 :“码上有前” 🚀 文章简介 :后端高频面试题 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 后端高频面试题--Mybatis篇 什么是Mybatis?Mybatis的优缺点?Mybatis的特点…...

【笔记】Helm-5 Chart模板指南-12 .helmignore文件
.helmignore文件 .helmignore文件用来指定您不想包含在您的helm chart中的文件。 如果该文件存在,helm package命令会在打包应用时忽略所有在.helmignore文件中匹配的文件。 有助于避免不需要的或敏感文件及目录添加到您的helm chart中。 .helmignore文件支持Uni…...
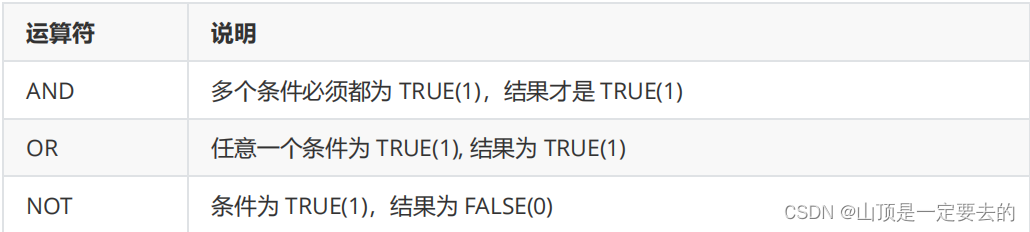
【MySQL】表的增删改查(基础)
MySQL表的增删改查(基础) 1. CRUD2. 新增(Create)2.1 单行数据全列插入2.2 多行数据 指定列插入 3. 查询(Retrieve)3.1 全列查询3.2 指定列查询3.3 查询字段为表达式3.4 别名3.5 去重:DISTINCT…...
Android矩阵Matrix动画缩放Bitmap移动手指触点到ImageView中心位置,Kotlin
Android矩阵Matrix动画缩放Bitmap移动手指触点到ImageView中心位置,Kotlin 借鉴 Android双指缩放ScaleGestureDetector检测放大因子大图移动到双指中心点ImageView区域中心,Kotlin(2)-CSDN博客 在此基础上实现手指在屏幕上点击后&…...

C语言:表达式求值
引言:在笔试中,有一类的题目,题目给出代码,要求分析得出输出结果。这类题目更加考察我们对于运算顺序和运算类型转换的理解。文章介绍了隐式类型转换和操作符注意点,希望增加读者对于表达式求值的理解。 1.隐式类型转…...
GO 的 Web 开发系列(五)—— 使用 Swagger 生成一份好看的接口文档
经过前面的文章,已经完成了 Web 系统基础功能的搭建,也实现了 API 接口、HTML 模板渲染等功能。接下来要做的就是使用 Swagger 工具,为这些 Api 接口生成一份好看的接口文档。 一、写注释 注释是 Swagger 的灵魂,Swagger 是通过…...
【极数系列】Flink集成KafkaSink 实时输出数据(11)
文章目录 01 引言02 连接器依赖2.1 kafka连接器依赖2.2 base基础依赖 03 使用方法04 序列化器05 指标监控06 项目源码实战6.1 包结构6.2 pom.xml依赖6.3 配置文件6.4 创建sink作业 01 引言 KafkaSink 可将数据流写入一个或多个 Kafka topic 实战源码地址,一键下载可用…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
