蓝桥杯每日一题----素数筛
素数筛
素数筛的作用是筛选出[2,N]范围内的所有素数,本次主要讲解两种方法,分别是埃氏筛和欧拉筛。证明时会提到唯一分解定理,如果不知道的小伙伴可以先去学一学,那我们开始啦!
1.埃氏筛
主要思想:当找到一个素数时,利用该素数把该素数的所有倍数筛掉。
时间复杂度: O ( n l o g ( l o g ( n ) ) ) O(nlog(log(n))) O(nlog(log(n)))
上代码,
//每个数的最小质因子//pre[i]表示i的最小质因子book[1] = 1;//记录是否为素数,1表示不是素数book[0] = 1;for(int i =2;i<book.length;i++) {if(book[i]==0) {// i是素数,筛掉素数的倍数 i=2 6 = 2+2+2for(int j = i+i;j<book.length&&j>0;j+=i) {book[j] = 1;} }}
问题:
-
为什么遍历到i时,若i没有被标记为合数(也就是没有被i前面的数筛掉),则一定是素数?
-
为什么for循环遍历到sqrt(N)就可以了?
先自己想一想哦,提示是唯一分解定理。
答案:
- 还记得唯一分解定理吗?一个正整数可以用若干个质数表示,假设当前正整数是n,它可以用质数 p 1 , p 2 . . . p k p_1,p_2...p_k p1,p2...pk表示, p 1 , p 2 . . . p k p_1,p_2...p_k p1,p2...pk一定比q小。假设q是合数,那么遍历到q,q一定会被 p 1 , p 2 . . . p k p_1,p_2...p_k p1,p2...pk筛掉。如果q是质数呢?他只能写出1*q的形式,它会被自己筛掉。
其实也就是证明sqrt(N)后面的合数一定会被小于sqrt(N)的数筛掉。设 N < n < N \sqrt{N}<n<N N<n<N且 a ∗ b = n a*b=n a∗b=n,若a<b,则 a < n < N a<\sqrt{n}<\sqrt{N} a<n<N,若a是素数,则n会被a筛掉,若a是合数,则a可以继续分解为更小的素数,而a和n都会被这个更小的素数筛掉,所以即便 N < n \sqrt{N}<n N<n,但是仅用小于 N \sqrt{N} N的数就可以把n筛掉,所以可以遍历到sqrt(N)。
2.欧拉筛
主要思想:埃氏筛的一部分时间耗在了重复的筛某些合数,比如18会被2和3筛掉。欧拉筛保证每个合数只被筛一次,因此也保证了 O ( n ) O(n) O(n)的时间复杂度。
时间复杂度: O ( n ) O(n) O(n)
上代码,
int count = 0;for (int i = 2; i < 20000005; i++) {//线性if (!visit[i]) {//如果i是一个质数prime[count++] = i;//记录当前已经找出来的所有的质数}for (int j = 0; j < count && i * prime[j] < 20000005; j++) {visit[i * prime[j]] = true;//用prime[j]筛掉了i * prime[j]。if (i % prime[j] == 0) break;//保证每个合数只被最小的质因子筛掉}}
问题:
- 为什么if语句满足后可以提前退出循环?
- 两个for循环嵌套如何实现的线性复杂度?
先自己想一想哦,提示是prime[j]是i的因子,你可以把式子写出来看看。
再讲答案之前先来捋一捋欧拉筛的结构,因为它不像埃氏筛那么直接。
首先一个for循环,接着如果当前的i是素数,则用另一个数组prime存一下,这个数组只存素数。
再来一个for循环,这个for循环就是用来筛合数的,遍历之前找到的所有素数,然后筛掉 p r i m e [ j ] ∗ i prime[j]*i prime[j]∗i。当满足if语句时,这一轮的筛合数可以提前退出了。
答案:
- 若此时if语句条件满足了,则prime[j]是i的因子,因此有 i = k ∗ p r i m e [ j ] i=k*prime[j] i=k∗prime[j]。如果此时没有退出for循环,会有 p r i m e [ j + 1 ] ∗ i prime[j+1]*i prime[j+1]∗i被prime[j+1]筛掉。 p r i m e [ j + 1 ] ∗ i = p r i m e [ j + 1 ] ∗ k ∗ p r i m e [ j ] = k ‘ ∗ p r i m e [ j ] prime[j+1]*i=prime[j+1]*k*prime[j]=k^`*prime[j] prime[j+1]∗i=prime[j+1]∗k∗prime[j]=k‘∗prime[j],这说明了什么?说明被prime[j+1]筛掉的 p r i m e [ j + 1 ] ∗ i prime[j+1]*i prime[j+1]∗i也会被prime[j]筛掉,这就重复筛了,怎么办?我们让每个数都被其最小的质因子筛掉,那么这里prime[j]就是 p r i m e [ j + 1 ] ∗ i prime[j+1]*i prime[j+1]∗i最小的质因子,因此j就不继续增大了,直接退出该循环。
- 因为保证了每个数只被筛一次,第二个for循环总共被执行n次,所有的数被筛完代码也就结束了。
例题
埃氏筛——最小质因子之和
参考代码:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Scanner;public class 最小质因子之和Easy {
public static void main(String[] args) throws IOException{//进行预处理f();//求2-n每个数对应的最小质因子sum();//求前缀和数组StreamTokenizer sc = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in))); Scanner scanner = new Scanner(System.in);sc.nextToken();int t = (int)sc.nval;while(t-- >0) {sc.nextToken();int n = (int)sc.nval;System.out.println(res[n]);}
}
static int book[] = new int[4000000];
static int pre[] = new int[4000000];
private static void f() {//埃氏筛模板//每个数的最小质因子//pre[i]表示i的最小质因子book[1] = 1;//记录是否为素数,1表示不是素数book[0] = 1;for(int i =2;i<book.length;i++) {if(book[i]==0) {// i是素数,筛掉素数的倍数 i=2 6 = 2+2+2pre[i] = i;//求的是质数的最小质因子for(int j = i+i;j<book.length&&j>0;j+=i) {if(book[j]==0) {pre[j] =i;}book[j] = 1;}}}}
static long res[] = new long[4000000];
private static void sum() {//一次求出i 2- n// 2-i的最小质因子之和,前缀和数组可以在O(n)for(int i=2;i<res.length;i++) {res[i] = res[i-1]+pre[i];}
}
}
欧拉筛——最小质因子之和困难版
参考代码:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;public class 最小质因子之和Hard {public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));int[] prime = new int[20000005];int[] f = new int[20000005];boolean[] visit = new boolean[20000005];int count = 0;for (int i = 2; i < 20000005; i++) {//线性if (!visit[i]) {//如果i是一个质数prime[count++] = i;f[i] = i;}for (int j = 0; j < count && i * prime[j] < 20000005; j++) {visit[i * prime[j]] = true;f[i * prime[j]] = prime[j];if (i % prime[j] == 0) break;}}long[] sum = new long[20000005];//前缀和数组for (int i = 2; i < f.length; i++) {//System.out.println(f[i]);sum[i] = sum[i - 1] + f[i];}int t = Integer.parseInt(br.readLine());while (t-- > 0) {int n = Integer.parseInt(br.readLine());System.out.println(sum[n]);}}
}
相关文章:

蓝桥杯每日一题----素数筛
素数筛 素数筛的作用是筛选出[2,N]范围内的所有素数,本次主要讲解两种方法,分别是埃氏筛和欧拉筛。证明时会提到唯一分解定理,如果不知道的小伙伴可以先去学一学,那我们开始啦! 1.埃氏筛 主要思想:当找到…...
20240212请问如何将B站下载的软字幕转换成为SRT格式?
20240212请问如何将B站下载的软字幕转换成为SRT格式? 2024/2/12 12:47 百度搜索:字幕 json 转 srt json srt https://blog.csdn.net/a_wh_white/article/details/120687363?share_token2640663e-f468-4737-9b55-73c808f5dcf0 https://blog.csdn.net/a_w…...

《CSS 简易速速上手小册》第6章:高级 CSS 技巧(2024 最新版)
文章目录 6.1 使用 CSS 变量进行设计:魔法配方的调配6.1.1 基础知识6.1.2 重点案例:创建可定制的主题6.1.3 拓展案例 1:响应式字体大小6.1.4 拓展案例 2:使用 CSS 变量创建动态阴影效果 6.2 calc(), min(), max() 等函数的应用&am…...

2024-02-11 多进程、多线程 work
1. 创建一个多进程服务器和多线程服务器 a. 多进程 #include<myhead.h> #define PORT 9999 //端口号 #define IP "192.168.125.113" //IP地址//定义信号处理函数,用于回收僵尸进程 void handler(int signo) {if(signo S…...

详解结构体内存对齐及结构体如何实现位段~
目录 编辑 一:结构体内存对齐 1.1对齐规则 1.2.为什么存在内存对齐 1.3修改默认对齐数 二.结构体实现位段 2.1什么是位段 2.2位段的内存分配 2.3位段的跨平台问题 2.4位段的应用 2.5位段使用的注意事项 三.完结散花 悟已往之不谏,知来者犹可…...
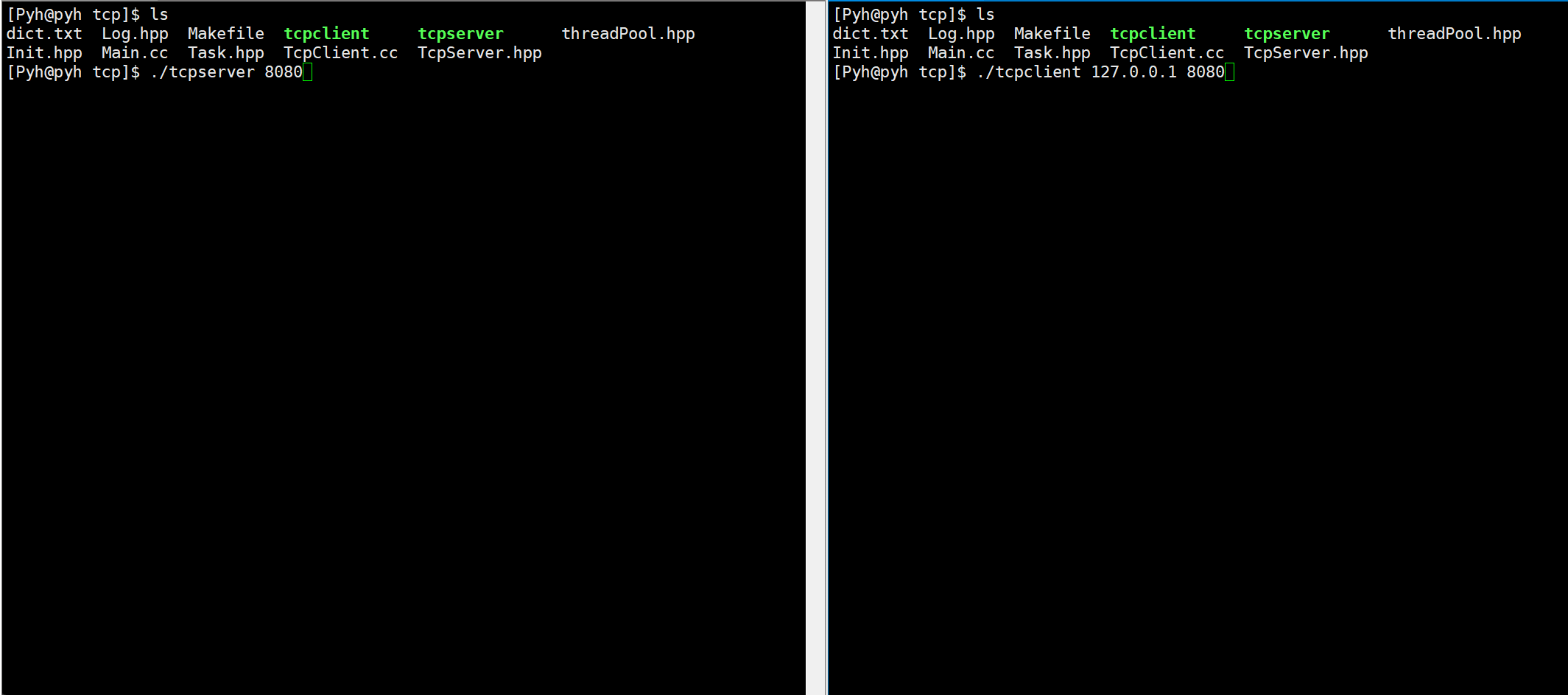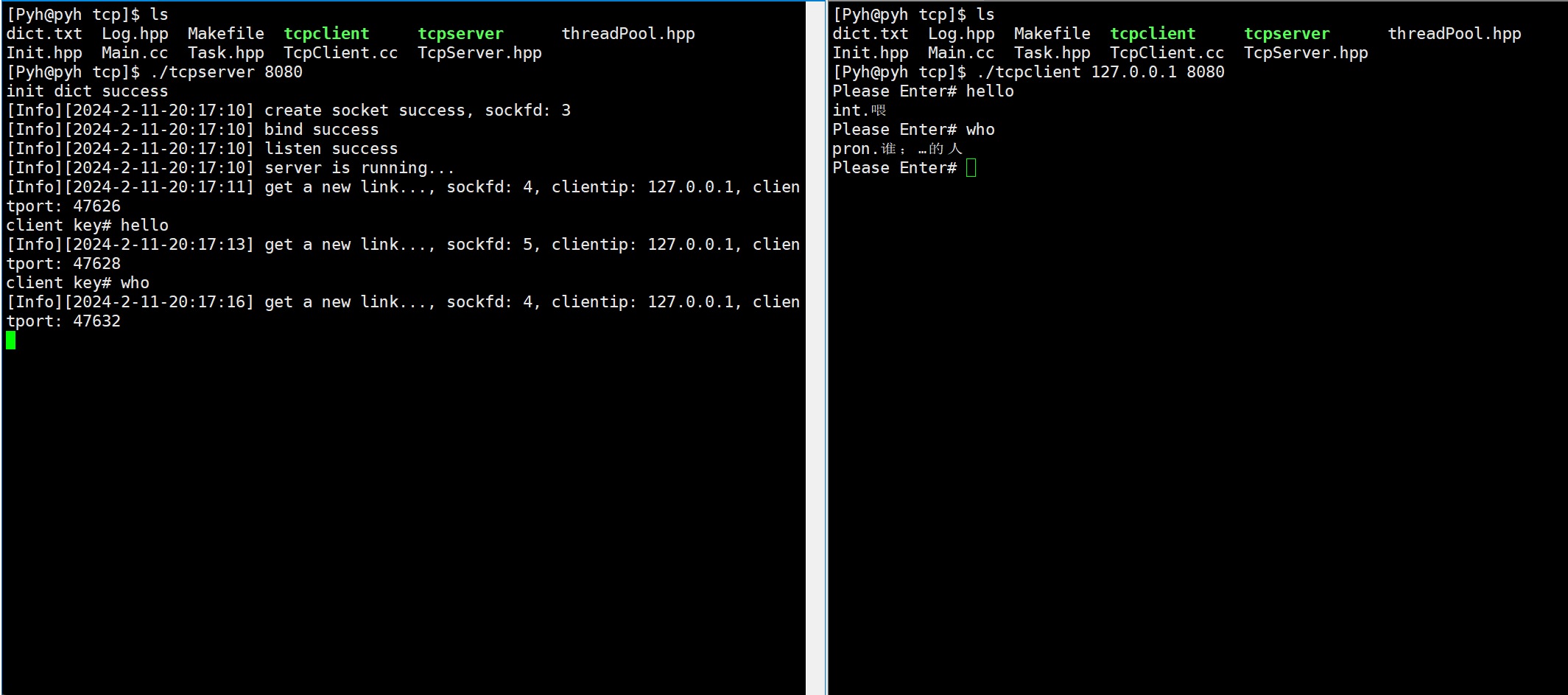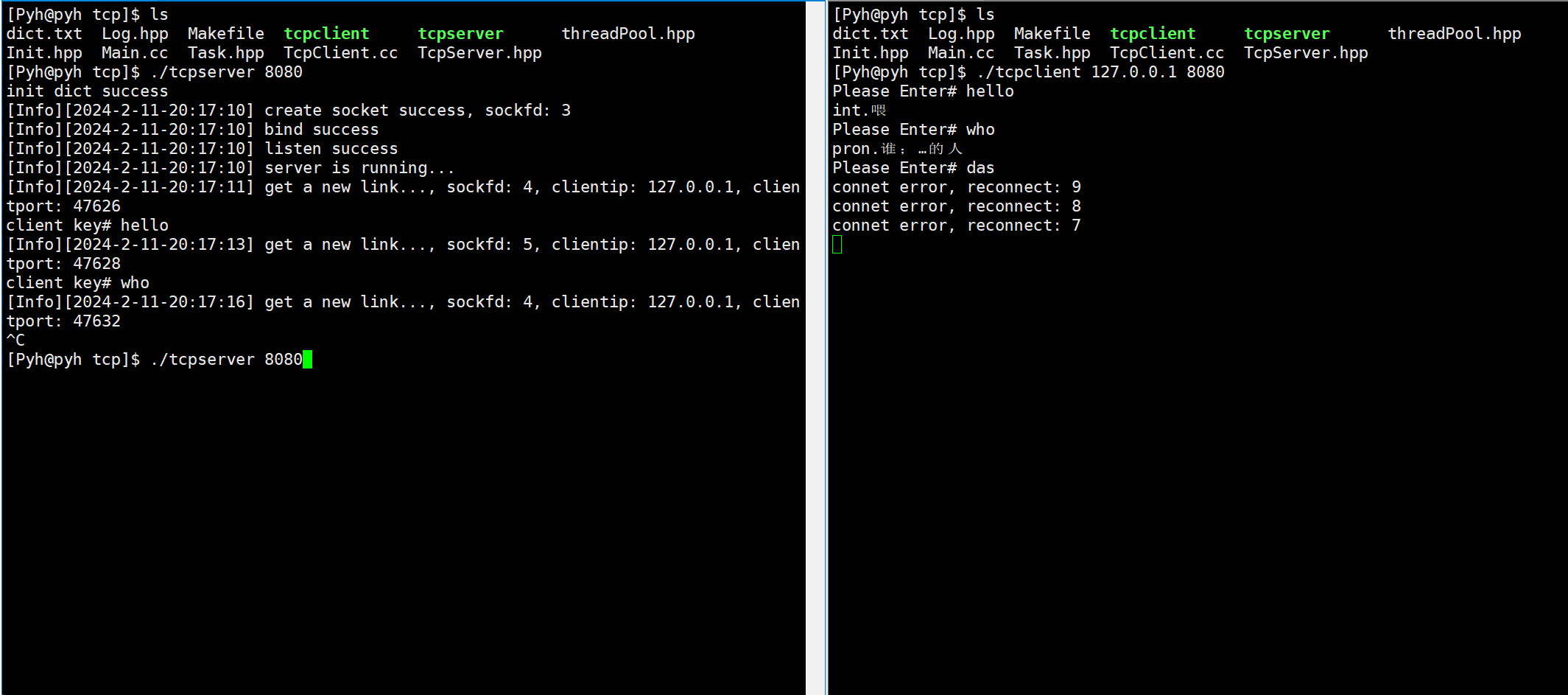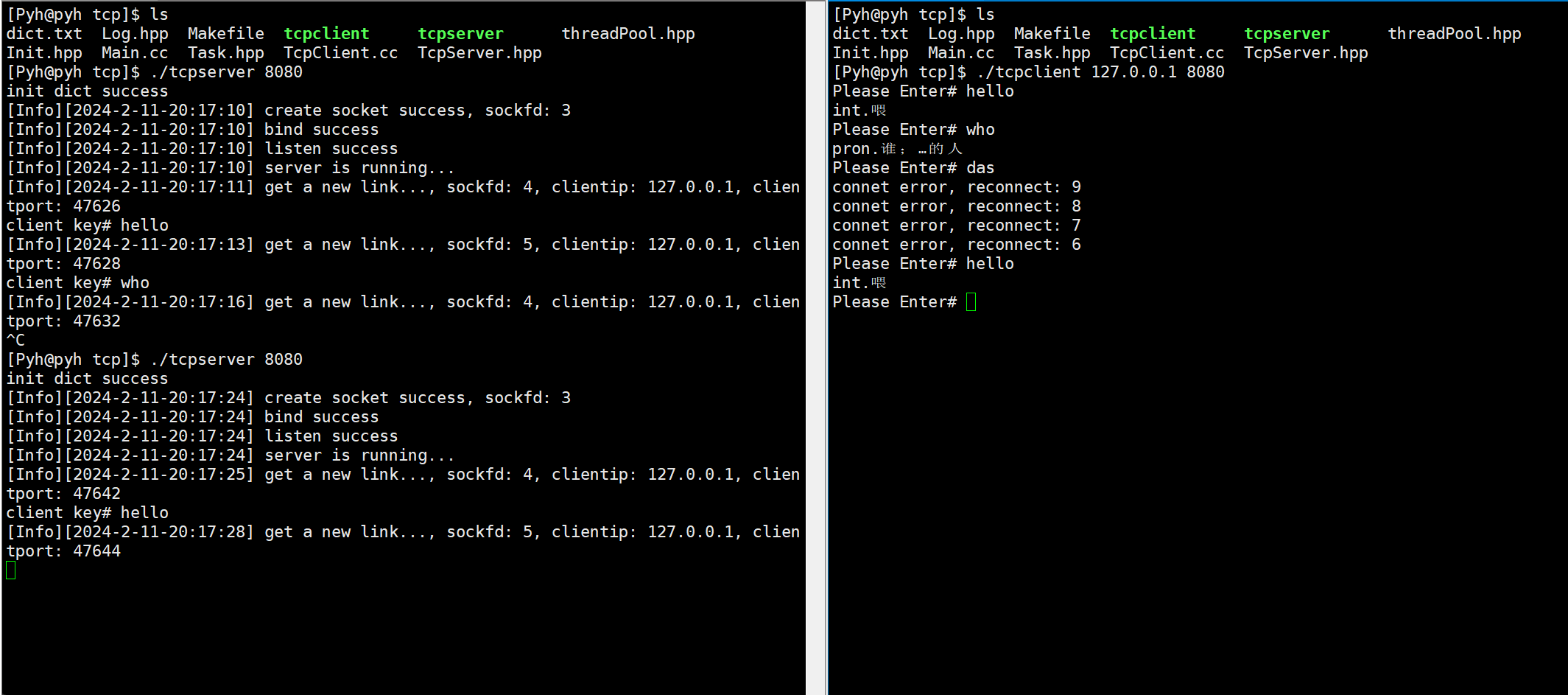
Linux网络编程——tcp套接字
文章目录 主要代码关于构造listen监听accepttelnet测试读取信息掉线重连翻译服务器演示 本章Gitee仓库:tcp套接字 主要代码 客户端: #pragma once#include"Log.hpp"#include<iostream> #include<cstring>#include<sys/wait.h…...

【计算机网络】协议层次及其服务模型
协议栈(protocol stack) 物理层链路层网络层运输层应用层我们自顶向下,所以从应用层开始探究应用层 协议 HTTP 提供了WEB文档的请求和传送SMTP 提供电子邮件报文的传输FTP 提供两个端系统之间的文件传输报文(message)是…...

prometheus之redis_exporter部署
下载解压压缩包 mkdir /opt/redis_exporter/ cd /opt/redis_exporter/ wget http://soft.download/soft/linux/prometheus/redis_exporter/redis_exporter-v1.50.0.linux-amd64.tar.gz tar -zxvf redis_exporter-v1.50.0.linux-amd64.tar.gz ln -s /opt/redis_exporter/redis_…...

js 解构赋值
搬运:JavaScript系列之解构赋值_js解构赋值-CSDN博客...

Vivado用ILA抓波形保存为CSV文件
将ILA观察到的波形数据捕获为CSV文件,抓10次,把文件合并,把源文件删除 运行方法:Vivado的 Tcl console 窗口输入命令 set tcl_dir F:/KLD_FPGA/Code/sim set tcl_filename TCL_ILA_TRIG_V1.2.tcl source $tcl_dir/$tcl_filenam…...
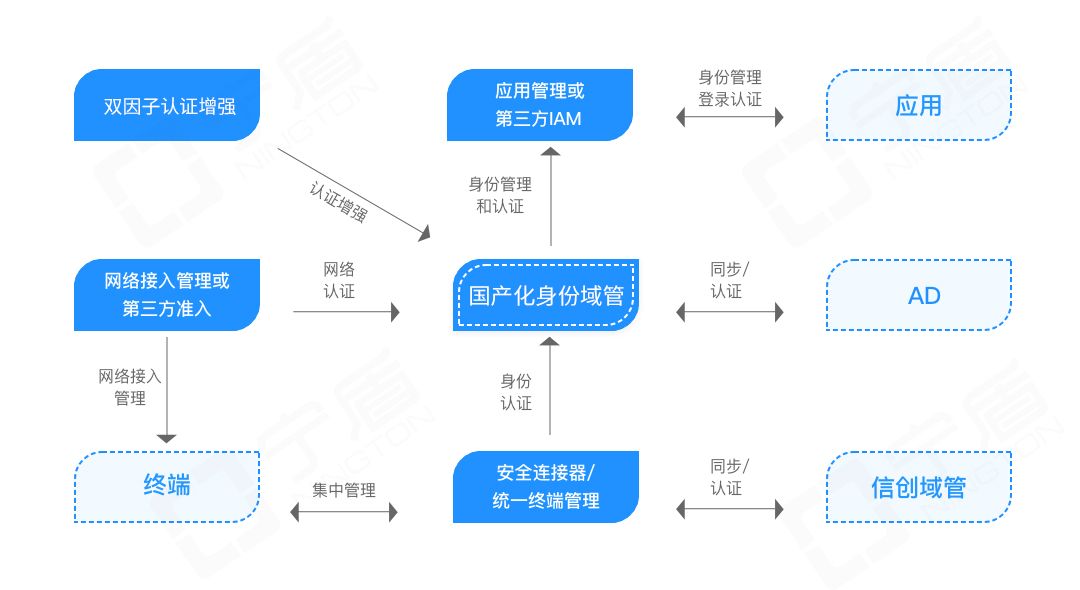
微软AD域替代方案,助力企业摆脱hw期间被攻击的窘境
在红蓝攻防演练(hw行动)中,AD域若被攻击成功,是其中一个扣分最多的一项内容。每年,宁盾都会接到大量AD在hw期间被攻击,甚至是被打穿的企业客户。过去,企业还会借助2FA双因子认证加强OA、Exchang…...

Git教程I
Git教程I 本地Git创建git仓库将修改存到暂存区将暂存区提交到当前分支查看提交历史回退版本恢复到更晚的版本创建新分支切换分支简单的分支合并冲突分支合并不使用fast forward: --no-ff 远程Git连接远程仓库将本地分支上传到远程仓库从远程仓库拉取 本地Git 学习如何使用本地…...
镜像验证)
containerd中文翻译系列(十)镜像验证
下面将介绍默认的 "bindir"ImageVerifier插件实现。 要启用图像验证,请在 containerd 配置中添加类似下面的一段: [plugins][plugins."io.containerd.image-verifier.v1.bindir"]bin_dir "/opt/containerd/image-verifier/b…...
)
假期day9(2024/2/14)
获取数据库查询的值并调用值使用函数:sqlite3_get_table 在回调函数中获取数据库查询值,无法在其他函数调用:使用函数sqlite3_exec(db, sql, select_callback, &flag, &errmsg) 创建表 create table if not exists 表名…...

Leetcode 674 最长连续递增序列
题意理解: 给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。 连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l < i < r,都有 nums[i…...

力扣题目训练(8)
2024年2月1日力扣题目训练 2024年2月1日力扣题目训练404. 左叶子之和405. 数字转换为十六进制数409. 最长回文串116. 填充每个节点的下一个右侧节点指针120. 三角形最小路径和60. 排列序列 2024年2月1日力扣题目训练 2024年2月1日第八天编程训练,今天主要是进行一些…...

理解JAVA EE设计模式
理解JAVA EE设计模式 在Web应用程序的设计和开发阶段,开发人员在开发类似的项目时可能会遇到相似的问题。每名开发人员可能会遇到的问题找出不同或相似的解决方案。但是,这导致一些时间和精力浪费在为相似的问题寻找解决方案上。因此,要啊节省时间和精力,需要记录常见问题…...

GEE:梯度提升树(Gradient Boosting Tree)回归教程(样本点、特征添加、训练、精度、参数优化)
作者:CSDN @ _养乐多_ 对于分类问题,这个输出通常是一个类别标签 ,而对于回归问题,输出通常是一个连续的数值。回归可以应用于多种场景,包括预测土壤PH值、土壤有机碳、土壤水分、碳密度、生物量、气温、海冰厚度、不透水面积百分比、植被覆盖度等。 本文将介绍在Google…...

k8s-资源限制与监控 15
资源限制 上传实验所需镜像 Kubernetes采用request和limit两种限制类型来对资源进行分配。 request(资源需求):即运行Pod的节点必须满足运行Pod的最基本需求才能 运行Pod。 limit(资源限额):即运行Pod期间,可能内存使用量会增加࿰…...

【Ubuntu】在.bashrc文件中误设置环境变量补救方法
这里是vim也不在PATH中了,因为 解决方法就是在输入vim之后提示的vim路径下用vim打开该文件,然后改回来...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
