Vue 全组件 局部组件
一、组件定义和使用
1、全局组件
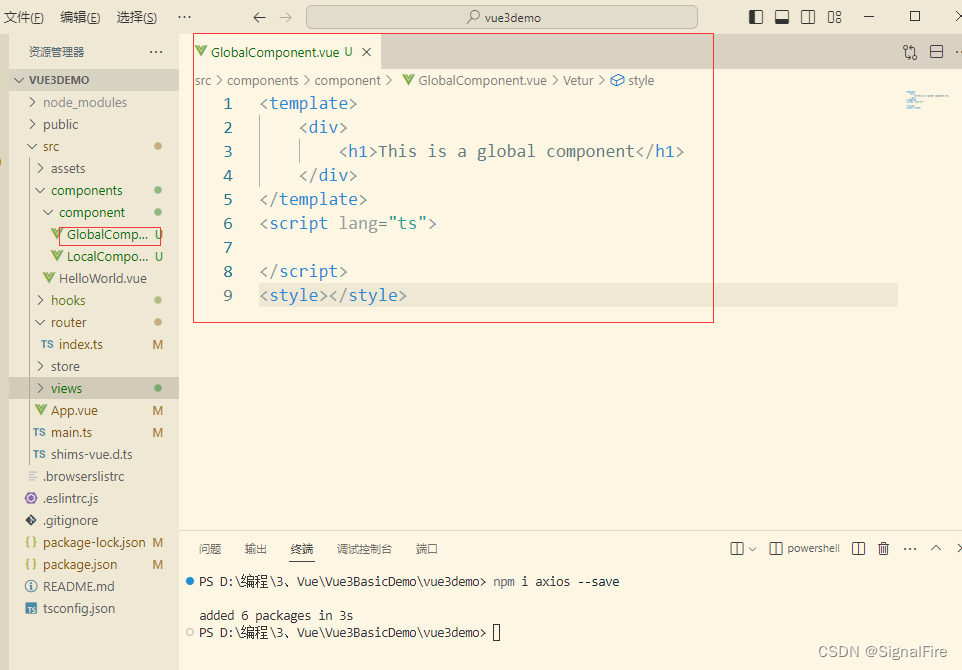
定义
<template>
<div>
<h1>This is a global component</h1>
</div>
</template>
<script lang="ts">
</script>
<style></style>
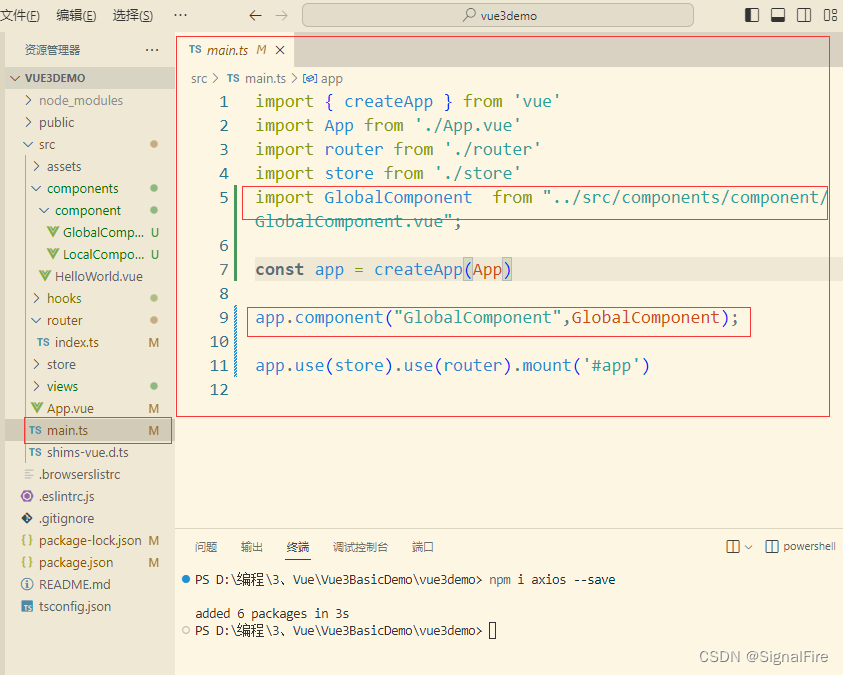
导入
全局组件在main.ts(Vue + TS的项目)引入,
或者在main.js(Vue + JS的项目)引入
import { createApp } from 'vue'
import App from './App.vue'
import router from './router'
import store from './store'
import GlobalComponent from "../src/components/component/GlobalComponent.vue";
const app = createApp(App)
app.component("GlobalComponent",GlobalComponent);
app.use(store).use(router).mount('#app')
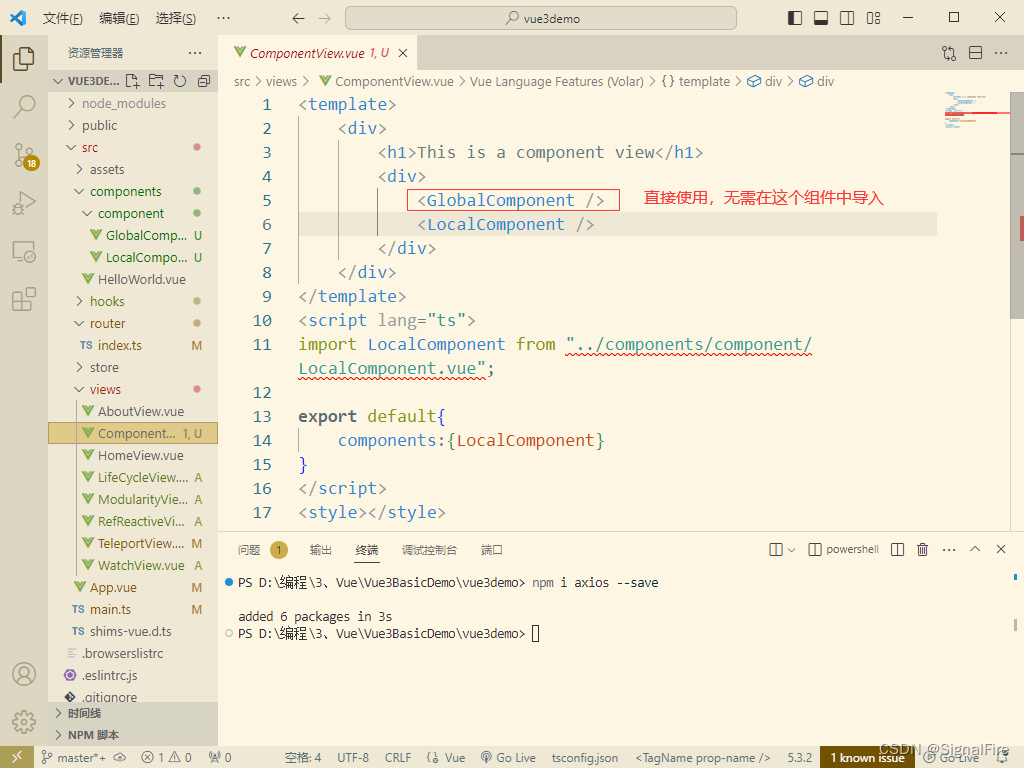
使用
全局组件可以在任意组件中使用,不需要再次导入
2、局部组件
定义
导入与使用

二、组件通信
1、props
(1)传递单个值
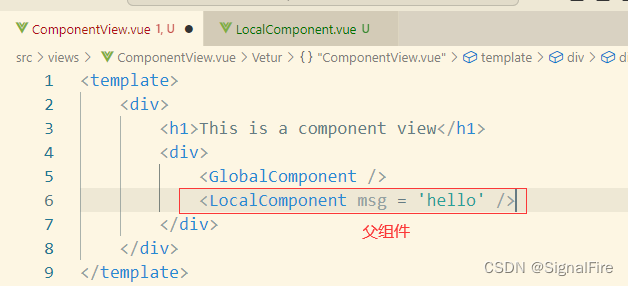
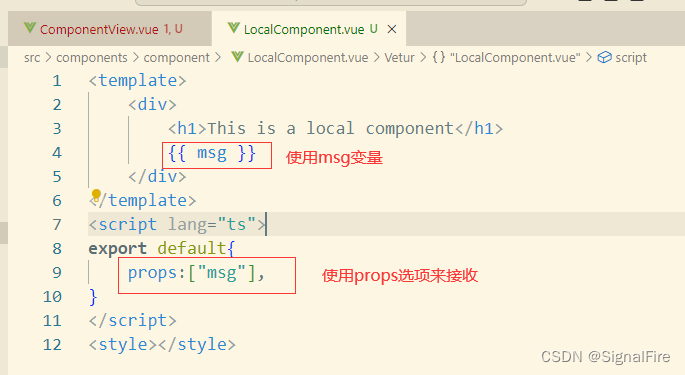
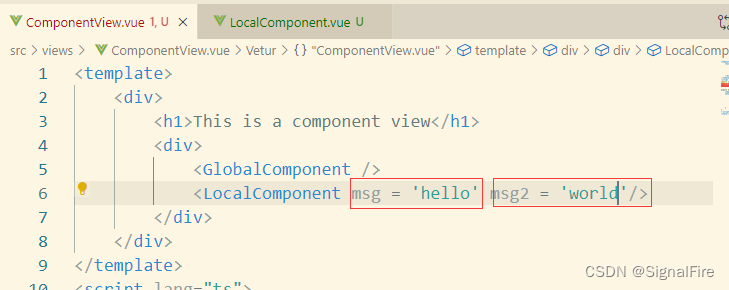
(2)传递多个值
如果传递的时对象,对象在被子组件的props接收时需要解构,依次写在props数组中

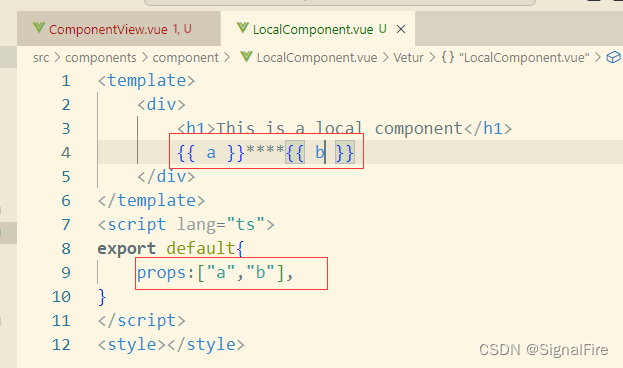
传递的如果是一个个的值,则直接在props数组中写入即可
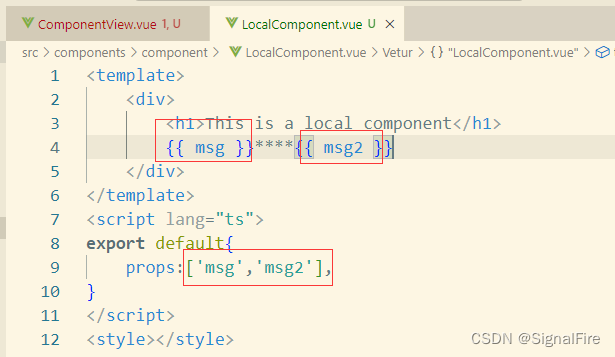
2、插槽
插槽的作用:让子组件可以接收父组件传过来的元素、组件
(1)匿名插槽
如果父元素只传递一个元素,或者传递的多个元素会在一个地方使用,那么可以使用匿名插槽
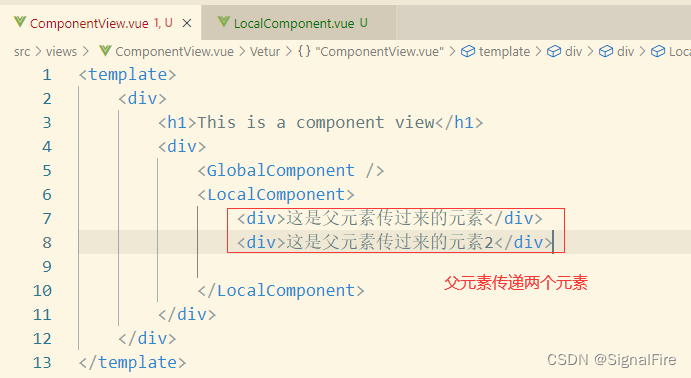
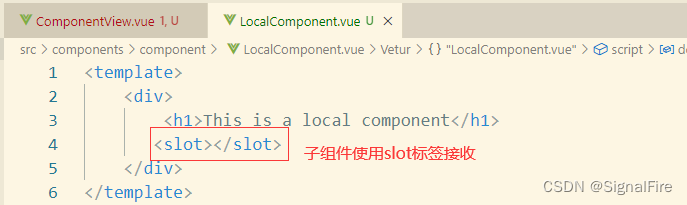

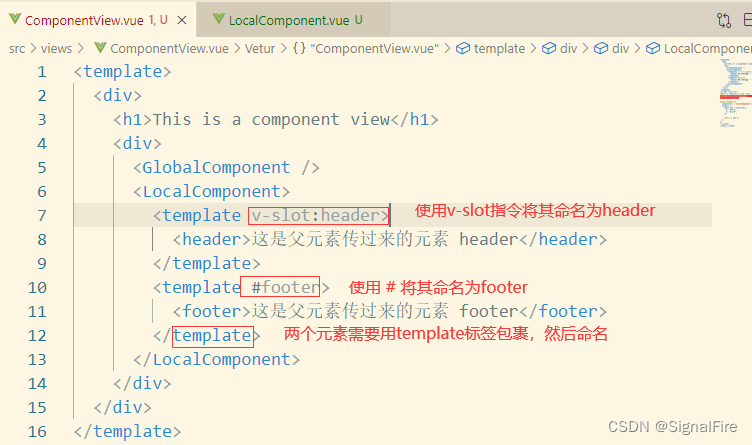
(2)具名插槽
父组件会传递多个元素,这些元素需要再不同的地方使用,这时需要使用具名插槽进行区分


(3)作用域插槽
父组件需要用到子组件中的数据时,可以使用作用域插槽将子组件的数据传递过去
子组件
<template>
<div>
<h1>This is a local component</h1>
<slot v-for="(item,index) in list" :item="item" :index="index"/>
</div>
</template>
<script lang="ts" setup>
const list = [1,2,3,4];
</script>
//父组件
<template>
<div>
<h1>This is a component view</h1>
<div>
<GlobalComponent />
<LocalComponent v-slot="slotProps">
<div>{{ slotProps.item }}*****{{ slotProps.index }}</div>
</LocalComponent>
</div>
</div>
</template>
//父组件写法二
<template>
<div>
<h1>This is a component view</h1>
<div>
<GlobalComponent />
<LocalComponent v-slot="{item,index}">
<div>{{ item }}*****{{ index }}</div>
</LocalComponent>
</div>
</div>
</template>
3、provide&inject
父组件给子组件传值,子组件使用props接收,如果孙子组件乃至重孙子组件要使用父组件的数据,那么就要一层层用props传递,特别麻烦。
父组件使用provide(提供)提供数据
子组件、孙子组件、重孙子组件....可以使用inject接收数据
//父组件
<template>
<div>
<LocalComponent />
</div>
</template>
<script setup lang="ts">
import LocalComponent from "../components/component/LocalComponent.vue";
import { provide, ref } from "vue";
const msg = ref('hello world');
provide('msg',msg);
</script>
//子组件
<template>
<div>
LocalComponent
<GrandChild />
</div>
</template>
<script lang="ts" setup>
import GrandChild from '../component/GrandChild.vue';
</script>
//孙子组件
<template>
<div>
<h1>This is a GrandChild component</h1>
{{ msg }}
</div>
</template>
<script lang="ts" setup>
import { inject } from "vue";
const msg = inject('msg');
</script>
<style></style>
4、事件通信
三、异步组件
相关文章:

Vue 全组件 局部组件
一、组件定义和使用 1、全局组件 定义 <template> <div> <h1>This is a global component</h1> </div> </template> <script lang"ts"> </script> <style></style> 导入 全局组件在main.tsÿ…...
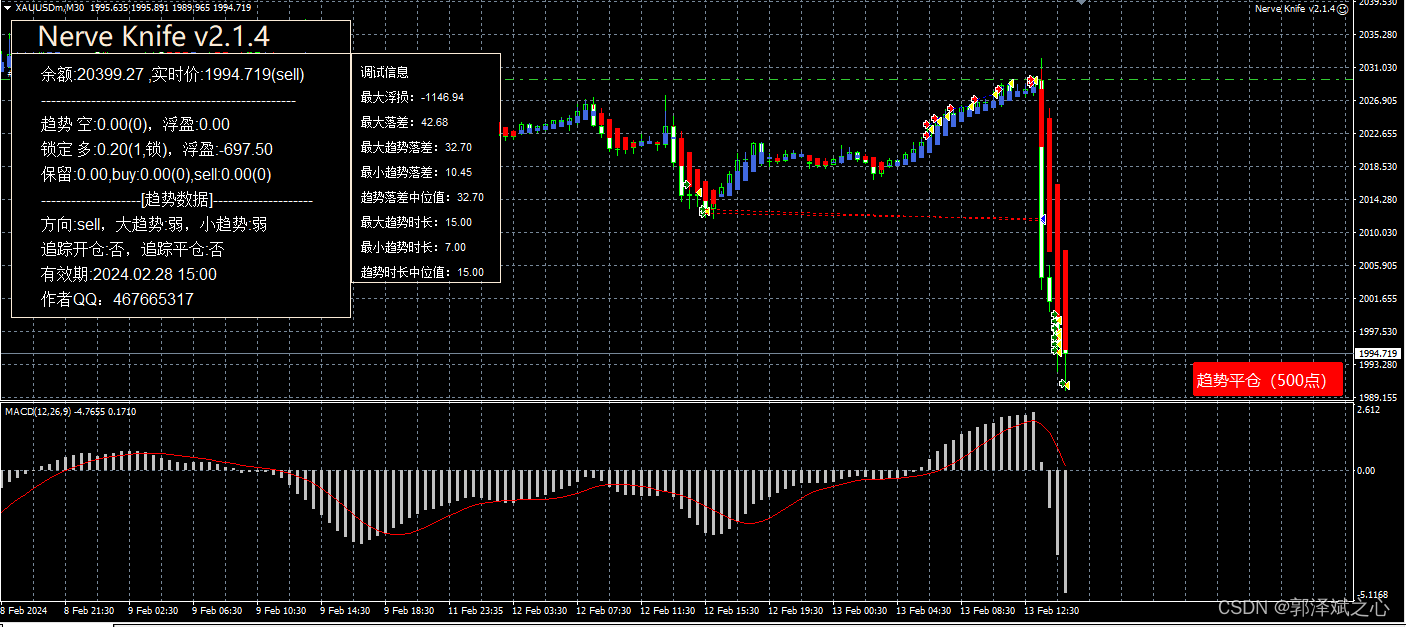
几个经典金融理论
完整EA:Nerve Knife.ex4黄金交易策略_黄金趋势ea-CSDN博客 一、预期效用理论 预期效用理论是描述人们在做出决策时如何考虑风险和不确定性的一种理论。该理论最初由经济学家冯诺伊曼(John von Neumann)和奥斯卡摩根斯坦恩(Oskar…...

c++语言max函数的使用
目录 头文件包含 使用语法 注意事项 头文件包含 首先,在使用std::max函数之前,需要包含头文件 <algorithm>。 #include <algorithm> 使用语法 std::max函数有两种重载形式,一种用于比较两个值,另一种用于比较多…...
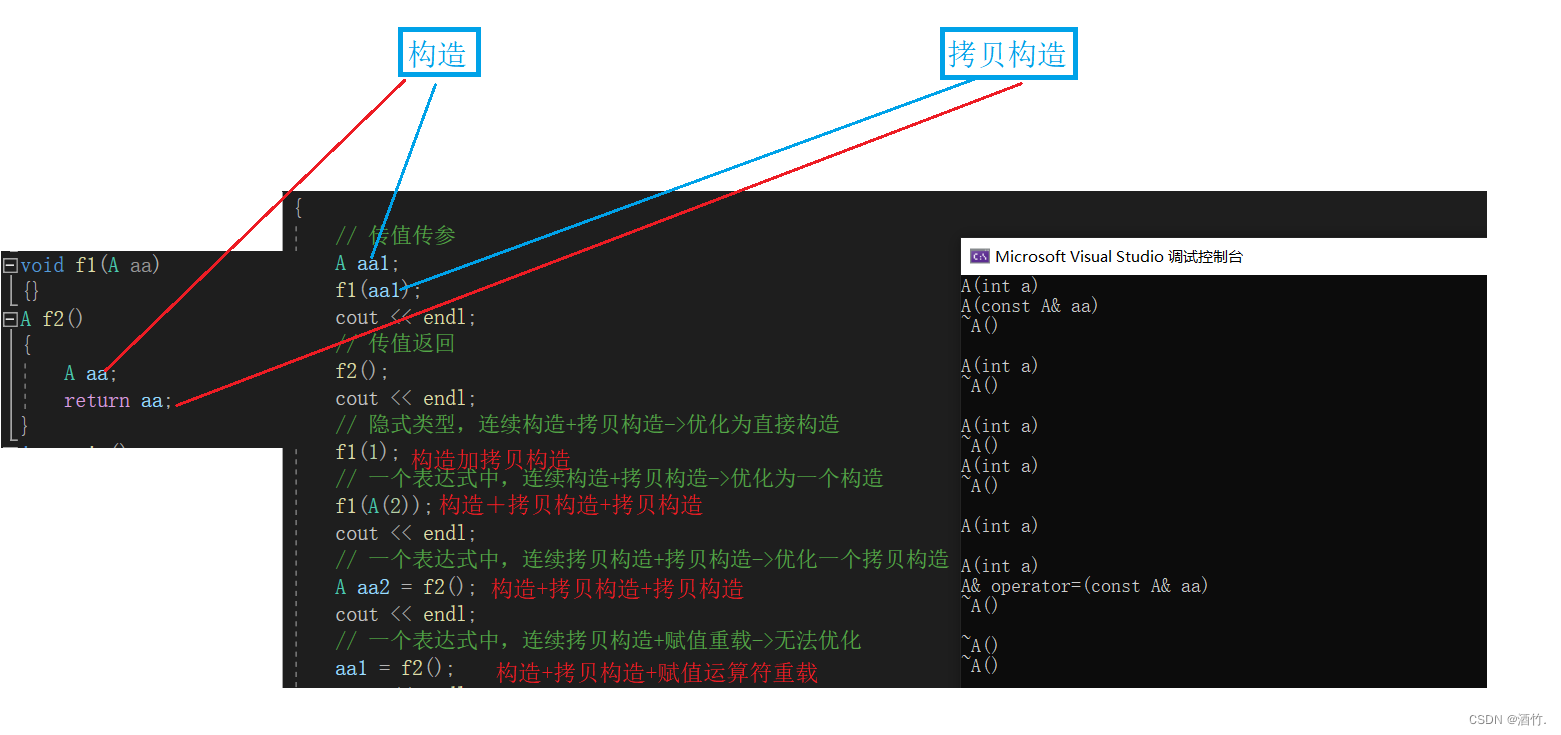
c++阶梯之类与对象(下)
前文: c阶梯之类与对象(上)-CSDN博客 c阶梯之类与对象(中)-CSDN博客 c阶梯之类与对象(中)< 续集 >-CSDN博客 1. 再谈构造函数 1.1 构造函数体赋值 在创建对象时&a…...
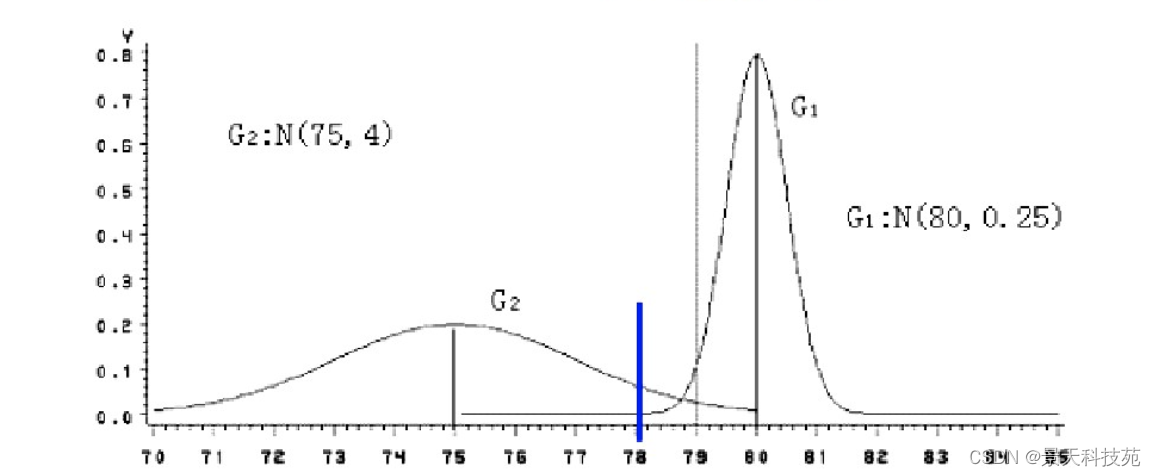
机器学习--K-近邻算法常见的几种距离算法详解
文章目录 距离度量1 欧式距离(Euclidean Distance)2 曼哈顿距离(Manhattan Distance)3 切比雪夫距离 (Chebyshev Distance)4 闵可夫斯基距离(Minkowski Distance)5 标准化欧氏距离 (Standardized EuclideanDistance)6 余弦距离(Cosine Distance)7 汉明距离(Hamming Distance)【…...
常用术语整理》)
<网络安全>《30 网络信息安全基础(1)常用术语整理》
1 肉鸡 所谓“肉鸡”是一种很形象的比喻,比喻那些可以随意被我们控制的电脑,对方可以是WINDOWS系统,也可以是UNIX/LINUX系统,可以是普通的个人电脑,也可以是大型的服务器,我们可以象操作自己的电脑那样来操…...
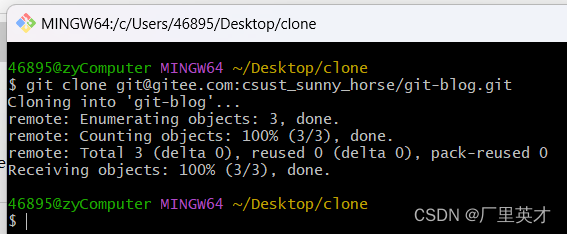
Git远程仓库的使用(Gitee)及相关指令
目录 1 远程仓库的创建和配置 1.1 创建远程仓库 1.2 设置SSH公钥 2 指令 2.1 git remote add 远端名称(一般为origin) 仓库路径 2.2 git remote 2.3 git push [-f] [--set-upstream] [远端名称 [本地分支名][:远端分支名]] 2.3 git clone url 2.4 git fetch 2.5 git p…...
vscode +markdown 的安装和使用
文章目录 前言一、vscode markdown 是什么?1.vscode是什么?2.markdown 是什么? 二、安装步骤1.下载2.安装 三、安装插件1.安装 Markdown All in One2.安装 Markdown Preview Enhanced3. Paste Image v1.0.44.LimfxCodeExv0.7.105.Code Spell …...
Python爬虫之自动化测试Selenium#7
爬虫专栏:http://t.csdnimg.cn/WfCSx 前言 在前一章中,我们了解了 Ajax 的分析和抓取方式,这其实也是 JavaScript 动态渲染的页面的一种情形,通过直接分析 Ajax,我们仍然可以借助 requests 或 urllib 来实现数据爬取…...

快速学习Spring
Spring 简介 Spring 是一个开源的轻量级、非侵入式的 JavaEE 框架,它为企业级 Java 应用提供了全面的基础设施支持。Spring 的设计目标是简化企业应用的开发,并解决 Java 开发中常见的复杂性和低效率问题。 Spring常用依赖 <dependencies><!-…...

c语言操作符(上)
目录 编辑 原码、反码、补码 1、正数 2、负数 3、二进制计算1-1 移位操作符 1、<<左移操作符 2、>>右移操作符 位操作符&、|、^、~ 1、&按位与 2、|按位或 3、^按位异或 特点 4、~按位取反 原码、反码、补码 1、正数 原码 反码 补码相同…...

vue3 可视化大屏自适应屏幕组件
首先定义了一个名叫ScreenContainerOptions的组件,需要传的参数如下 export type ScreenContainerOptions {width?: string | numberheight?: string | numberscreenFit?: boolean // 是否开启屏幕自适应,不然会按比例显示 } 组件的主要代码如下 …...

SpringCloud入门概述
1. 介绍 Spring Cloud 1.1 什么是 Spring Cloud Spring Cloud 是一个基于 Spring Boot 的微服务架构开发工具集,它为开发者提供了一系列开箱即用的工具和库,用于构建分布式系统中的微服务架构。Spring Cloud 提供了诸如服务发现、配置中心、负载均衡、…...

刷题计划_冲绿名
现在 rating 是 1104 准备刷 100道 1200的题,把实力提升到 1200 ,上一个绿名 每一个分数段的题都写一百道,争取早日上蓝 现在 虽然 cf 里面显示写了一些这个分数段的题,但是自己训练的时候,其实是没有训练一道这个分…...

【微信小程序开发】小程序版的防抖节流应该怎么写
由于微信小程序与普通网页的开发、编译、运行机制都有所不同,在防抖节流的方法使用上也就需要我们做一些比较棘手的适配操作。常见的H5开发的防抖节流此处就不再分享了,网上有太多的教程,或者直接问那群AI即可。 OK,言归正传&…...

单片机学习笔记---蜂鸣器播放提示音音乐(天空之城)
目录 蜂鸣器播放提示音 蜂鸣器播放音乐(天空之城) 准备工作 主程序 中断函数 上一节讲了蜂鸣器驱动原理和乐理基础知识,这一节开始代码演示! 蜂鸣器播放提示音 先创建工程:蜂鸣器播放提示音 把我们之前模块化的…...
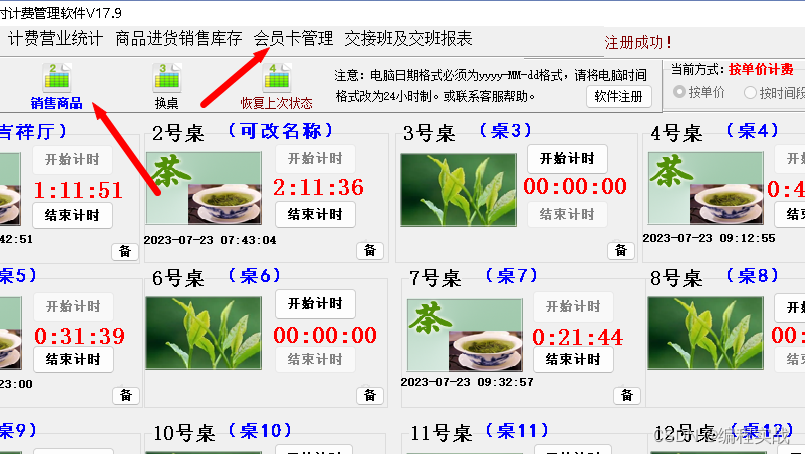
软件实例分享,茶楼收银软件管理系统,支持计时计费商品销售会员管理定时语音提醒功能
软件实例分享,茶楼收银软件管理系统,支持计时计费商品销售会员管理定时语音提醒功能 一、前言 以下软件教程以 佳易王茶社计时计费管理系统软件V18.0为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 问:这个软…...
clang前端
Clang可以处理C、C和Objective-C源代码 Clang简介 Clang可能指三种不同的实体: 前端(在Clang库中实现)编译驱动程序(在clang命令和Clang驱动程序库中实现)实际的编译器(在clang-ccl命令中实现࿰…...
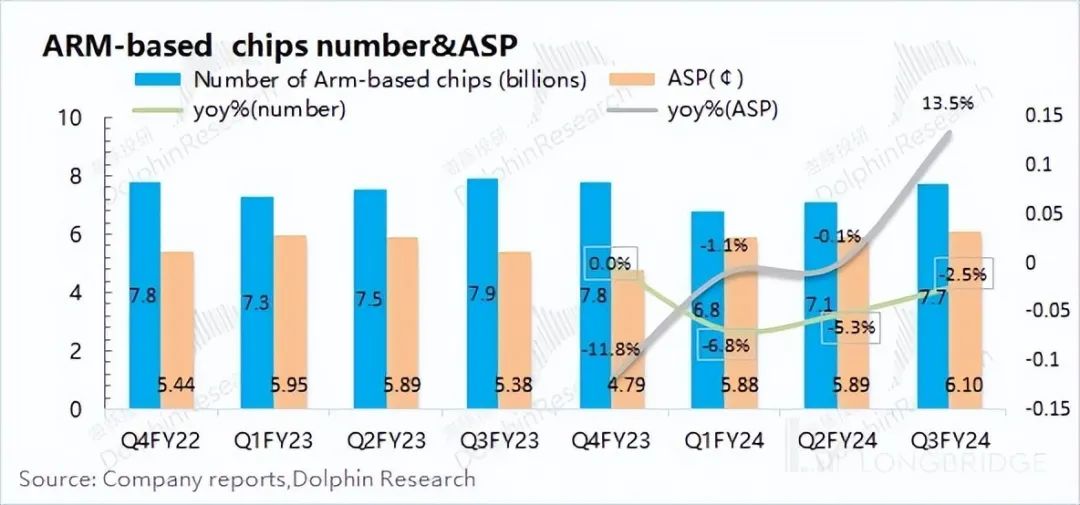
ARM:AI 的翅膀,还能飞多久?
ARM(ARM.O)于北京时间 2024 年 2 月 8 日上午的美股盘后发布了 2024 年第三财年报告(截止 2023 年 12 月),要点如下: 1、整体业绩:收入再创新高。ARM 在 2024 财年第三季度(即 23Q4…...
【C语言】常见字符串函数的功能与模拟实现
目录 1.strlen() 模拟实现strlen() 2.strcpy() 模拟实现strcpy() 3.strcat() 模拟实现strcat() 4.strcmp() 模拟实现strcmp() 5.strncpy() 模拟实现strncpy() 6.strncat() 模拟实现strncat() 7.strncmp() 模拟实现strncmp() 8.strstr() 模拟实现strstr() 9.str…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
