量子算法入门——2.线性代数与复数
参考资料:
【【零基础入门量子计算-第03讲】线性代数初步与复数】
来自b站up:溴锑锑跃迁
建议关注他的更多高质量文章:CSDN:【溴锑锑跃迁】
0. 前言
强烈建议搭配b站原视频进行观看,这只是我当时看的笔记,读懂这堂课的内容可能需要:线性代数(初等变换、列向量)、离散数学(群)、高等数学(极限等价无穷小部分)的知识储备
1. 向量的表示与运算
-
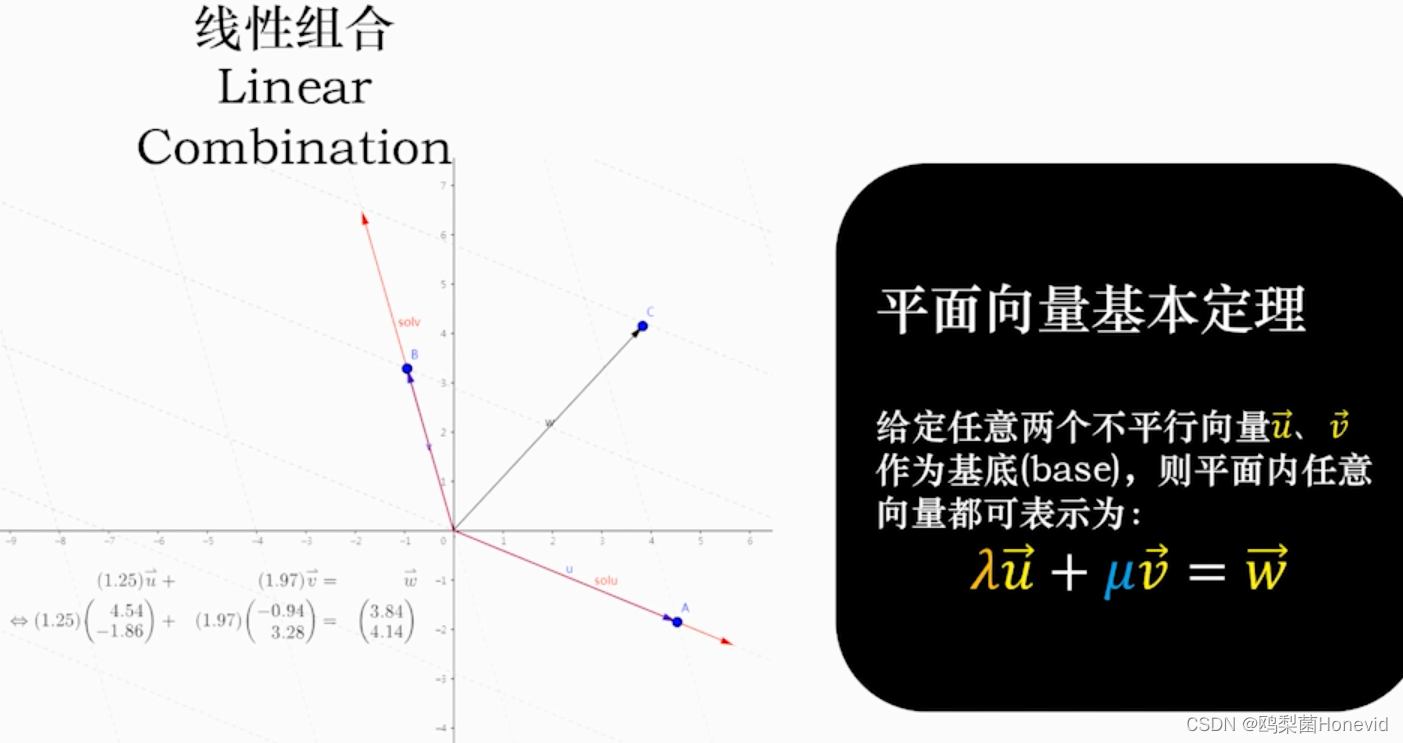
平面向量基本定理,可推广至三维或更多维度情况
-
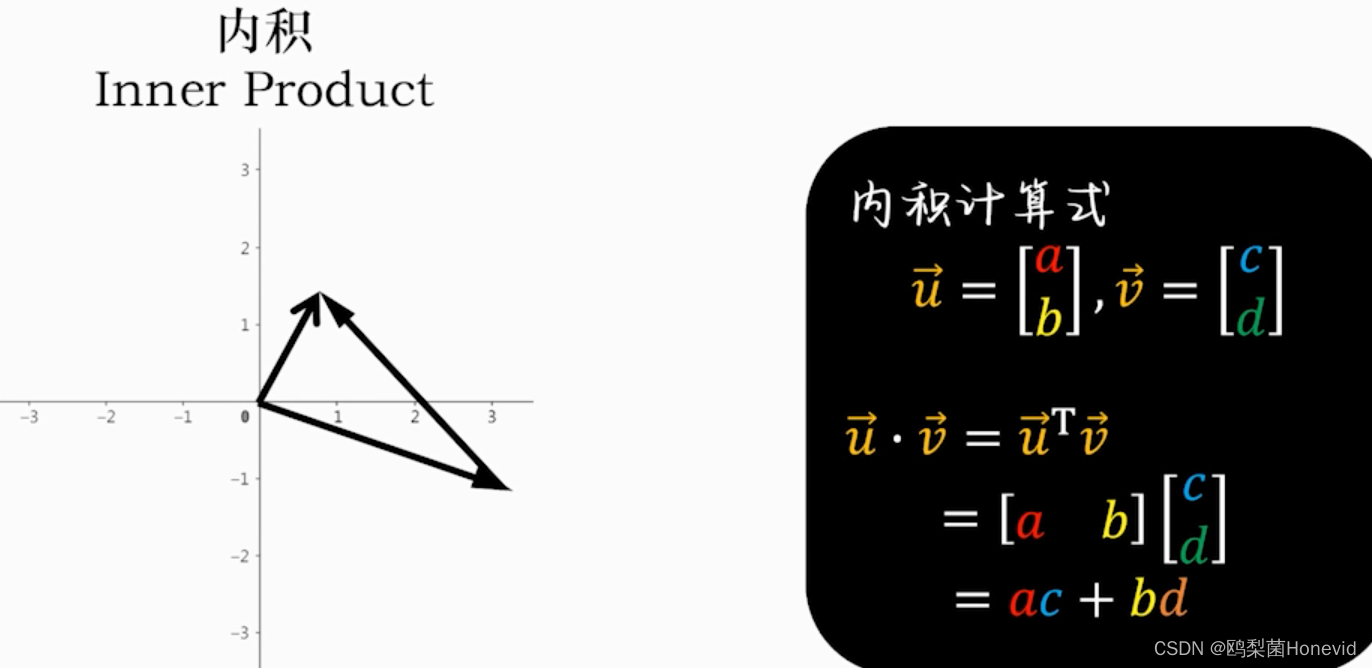
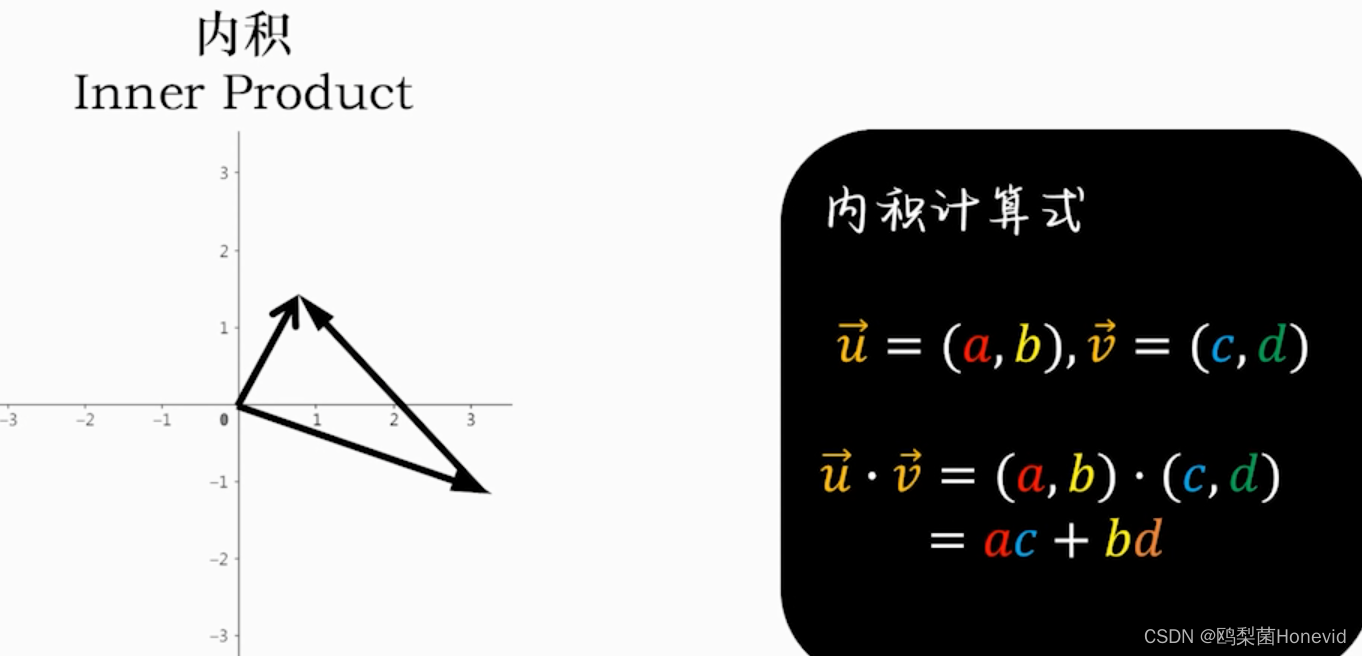
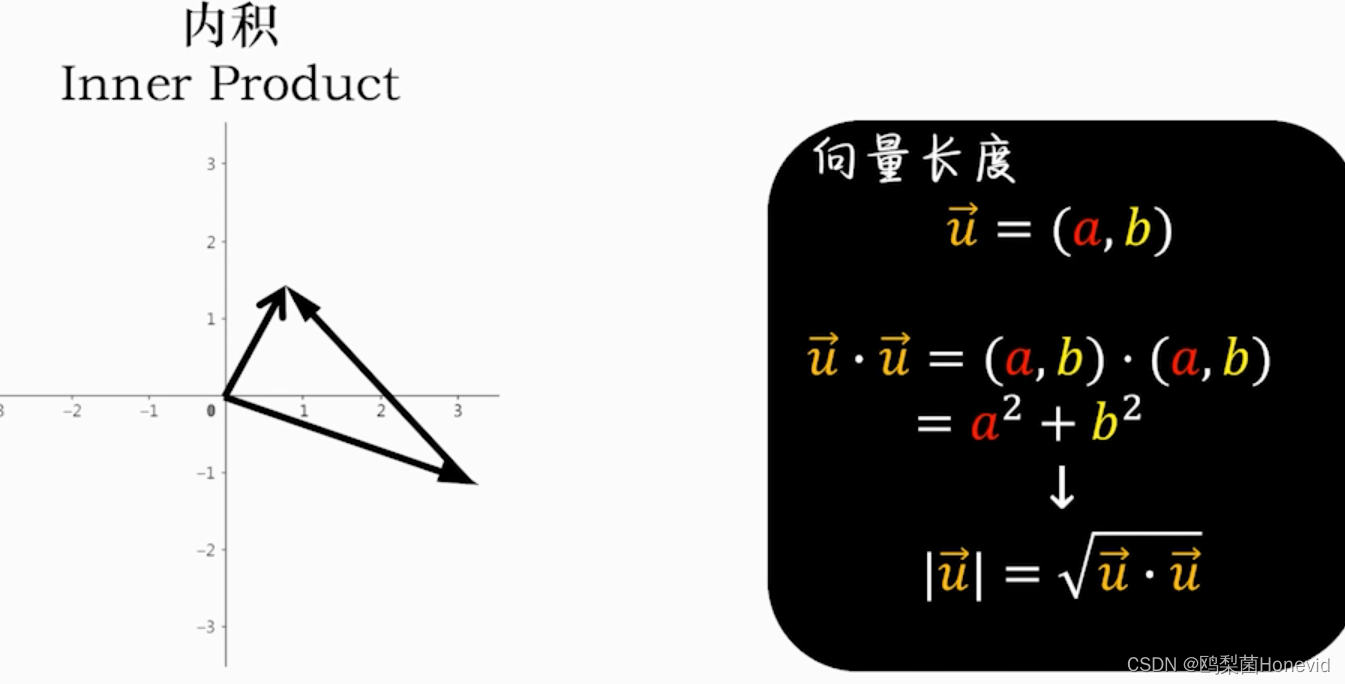
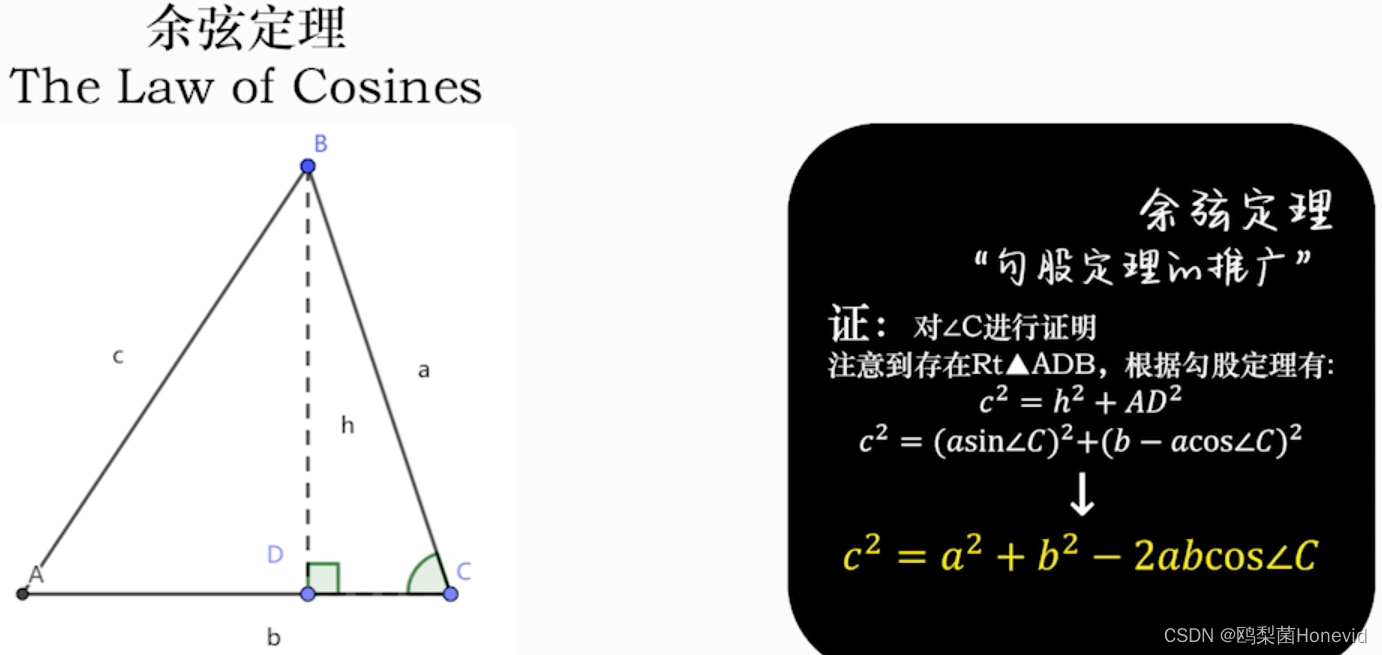
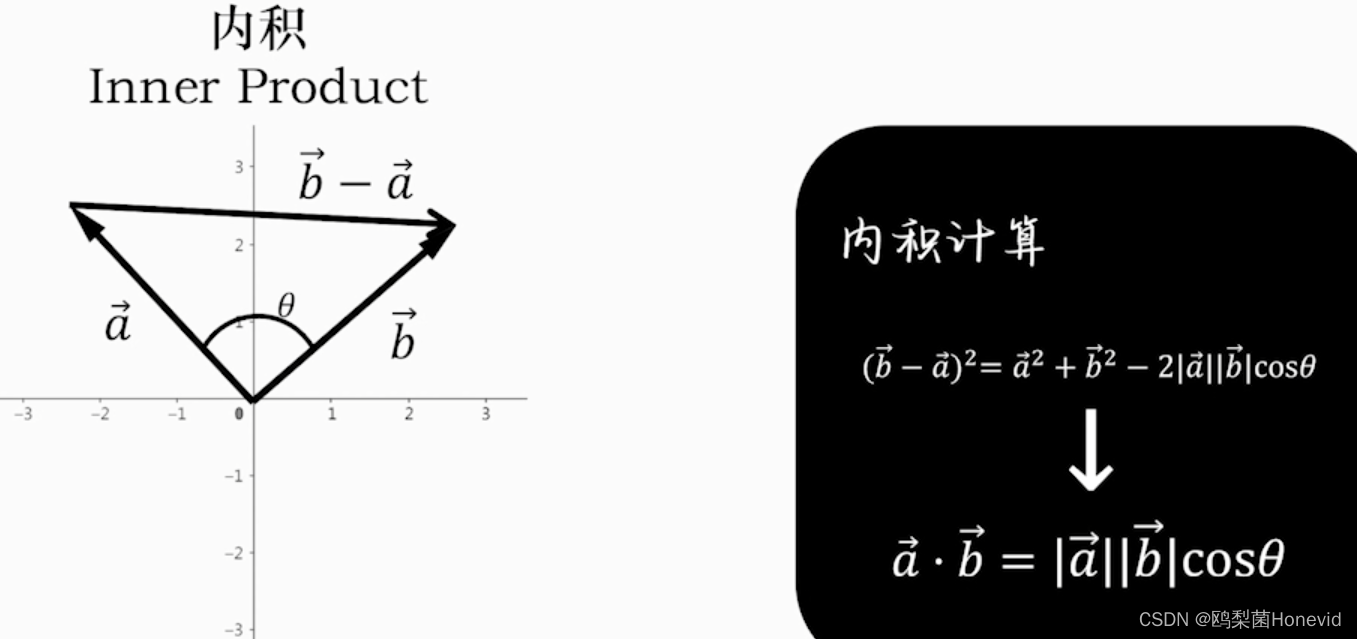
内积=点乘,得到标量
-
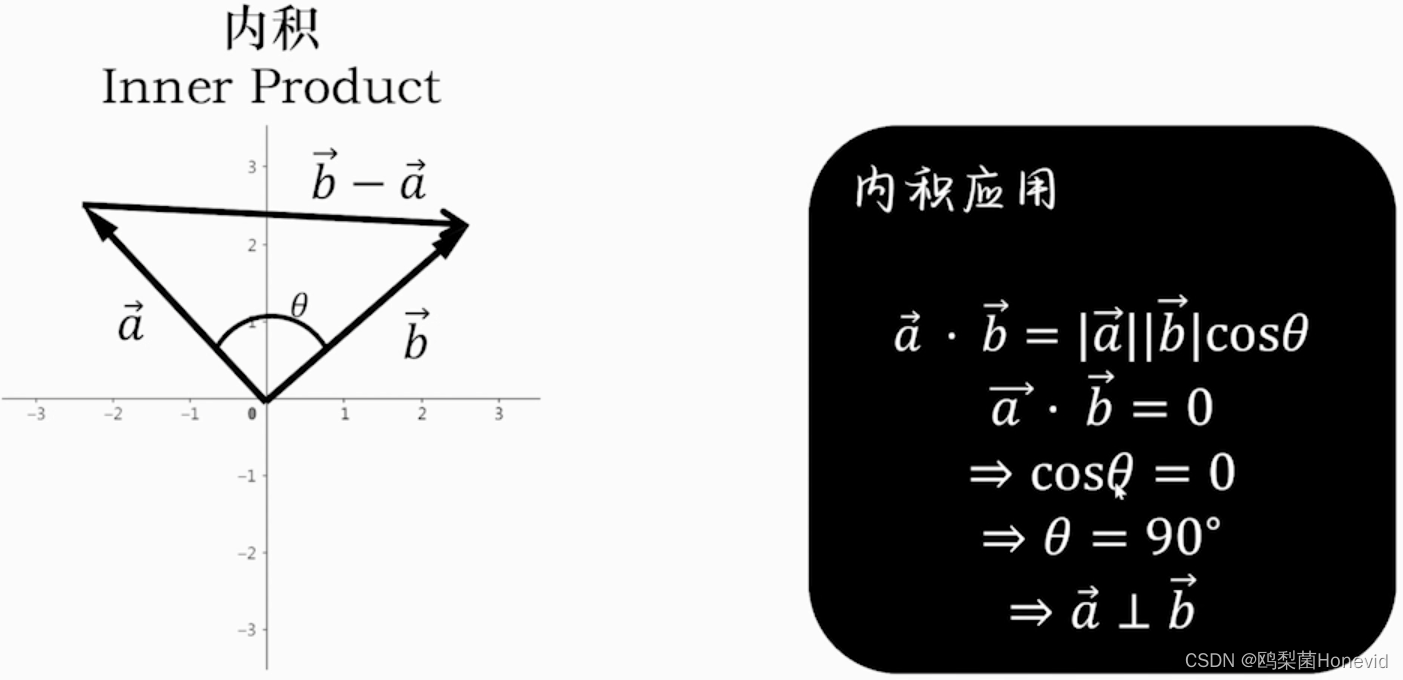
正交基——内积为零的两向量相互垂直,称为正交基底
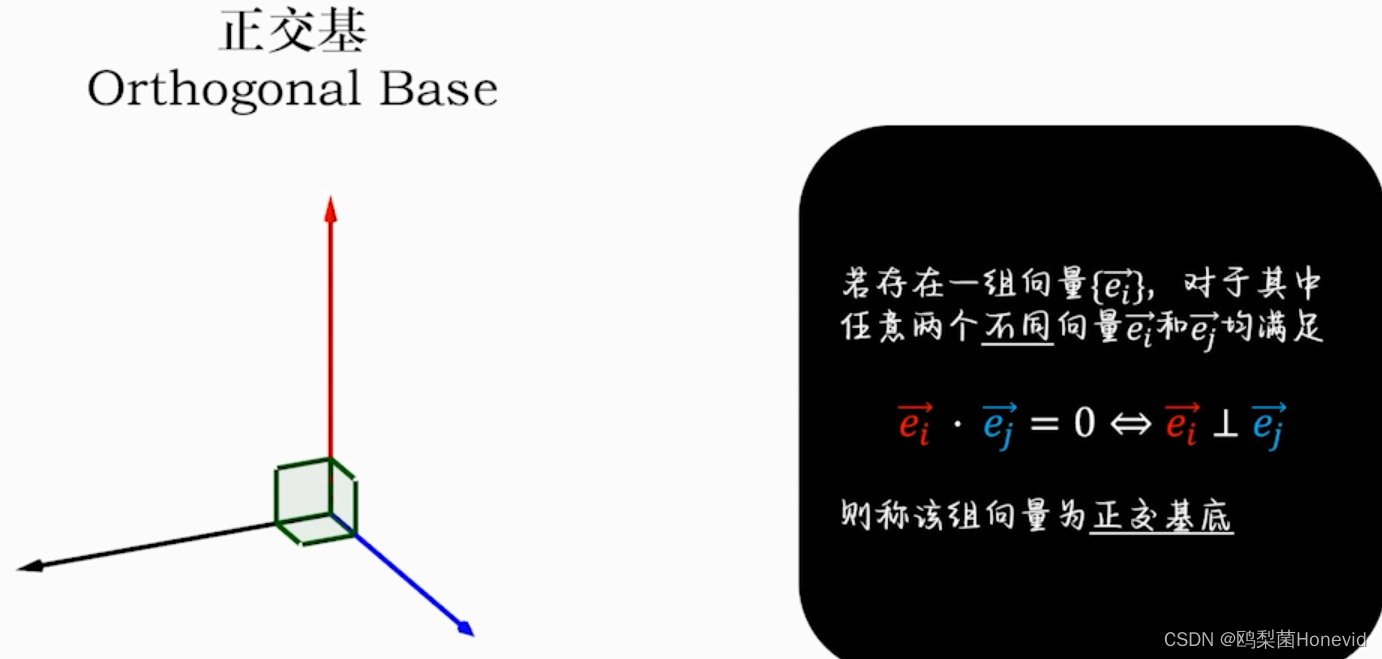


2. 矩阵表示及其运算


-
矩阵运算法则
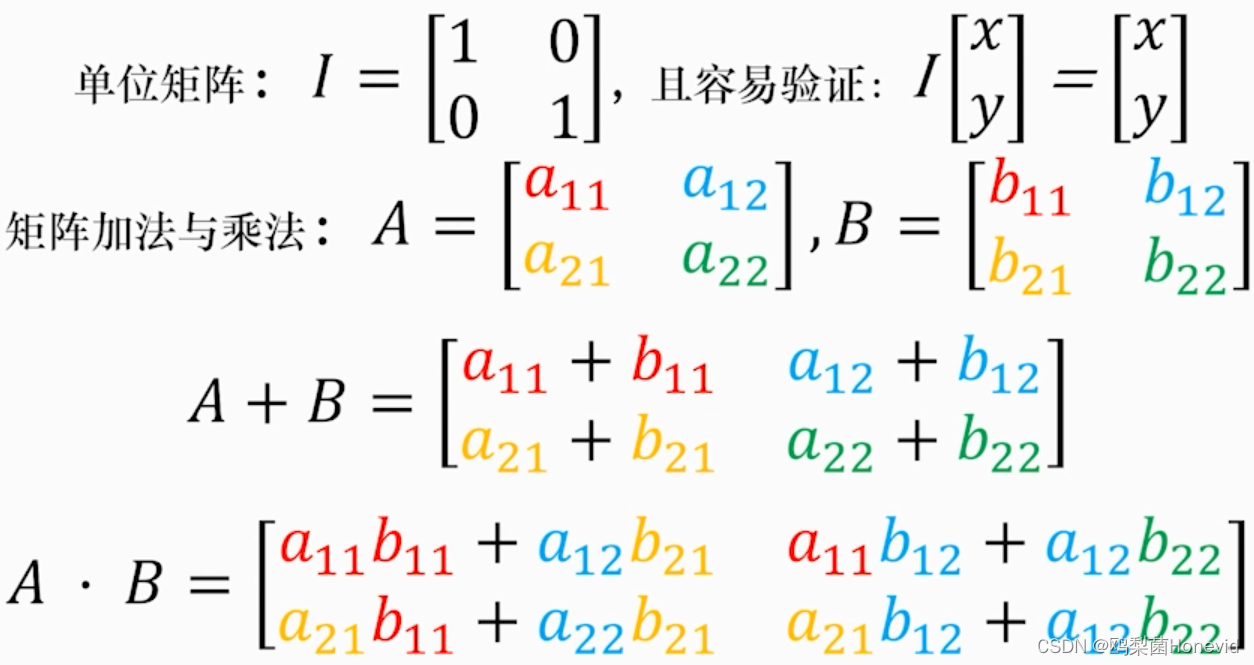

-
矩阵初等变换

-
逆矩阵(up的视频里面这里要是有如下文字提示可能会更好)
设有矩阵 A A A和矩阵 B B B,有 A B = E AB=E AB=E(其中 E E E表示为单位矩阵,有的地方会用 I I I表示),则B为A的逆矩阵,即有 B = A − 1 B=A^{-1} B=A−1
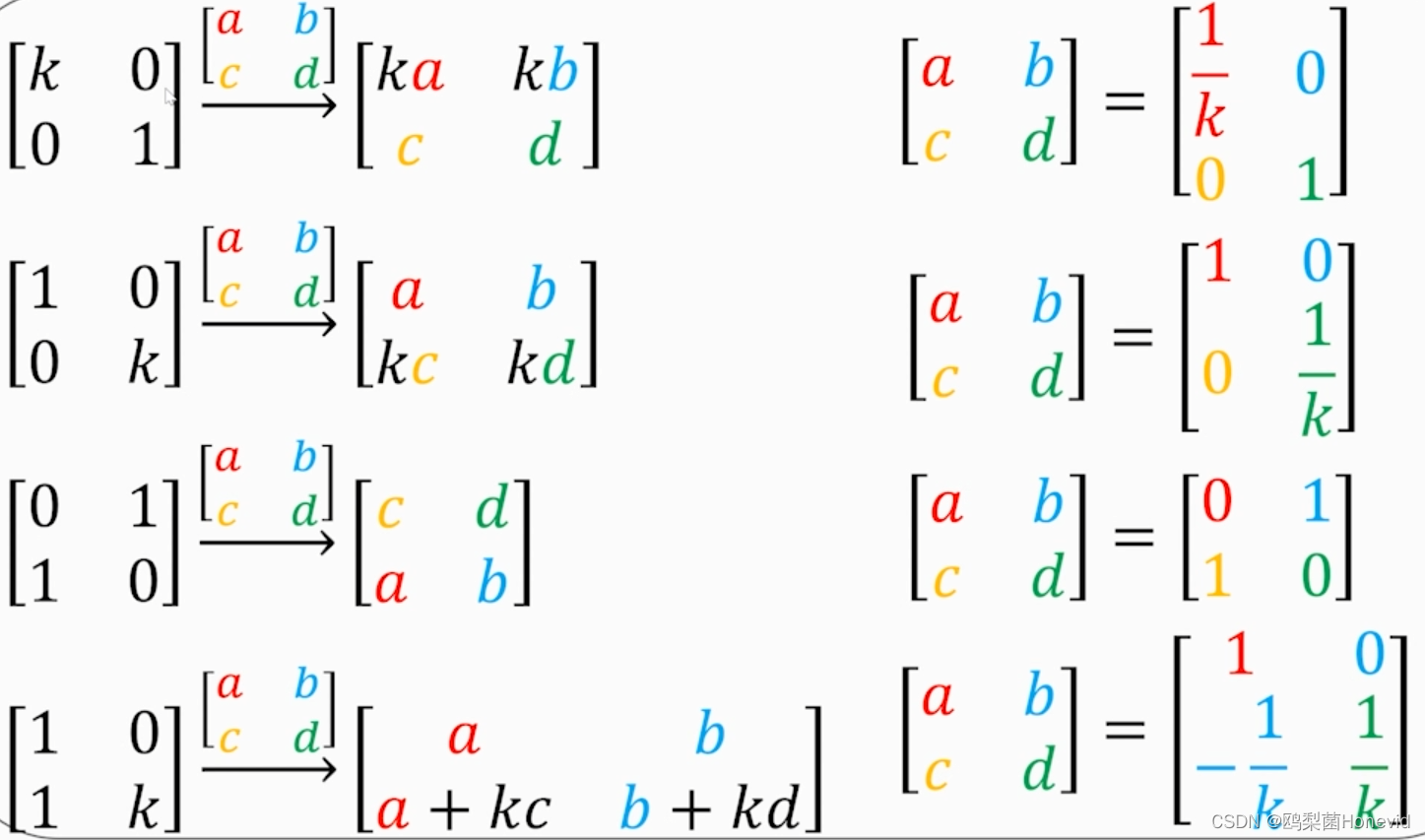
对之前鸡兔同笼所列矩阵求解过程进行详细展示,关键是求逆矩阵左乘到右侧



矩阵等式的理解方式


- 理解方式一:(上图左)映射、矩阵变换,即从一个向量向另一个向量变换=矩阵
- 理解方式二:(上图右)用坐标系本身代表的基底去组合成新的向量


旋转矩阵:





3. 群的简介(离散数学相关)
1. 群的定义
-
考虑一个集合G并对其中元素定义/指定一种操作称为群乘法
-
集合G在指定群乘法后其中元素应当满足以下四条性质才能被称作群
-
封闭性

-
结合律

-
单位元

-
逆元素

 日是e的象形
日是e的象形


下面上三个实例



同态映射:先作用再乘法=先乘法再作用

即: e x ∗ e y = e x + y e^x*e^y=e^{x+y} ex∗ey=ex+y,即 f ( x ) + f ( y ) = f ( x + y ) f(x)+f(y)=f(x+y) f(x)+f(y)=f(x+y) -

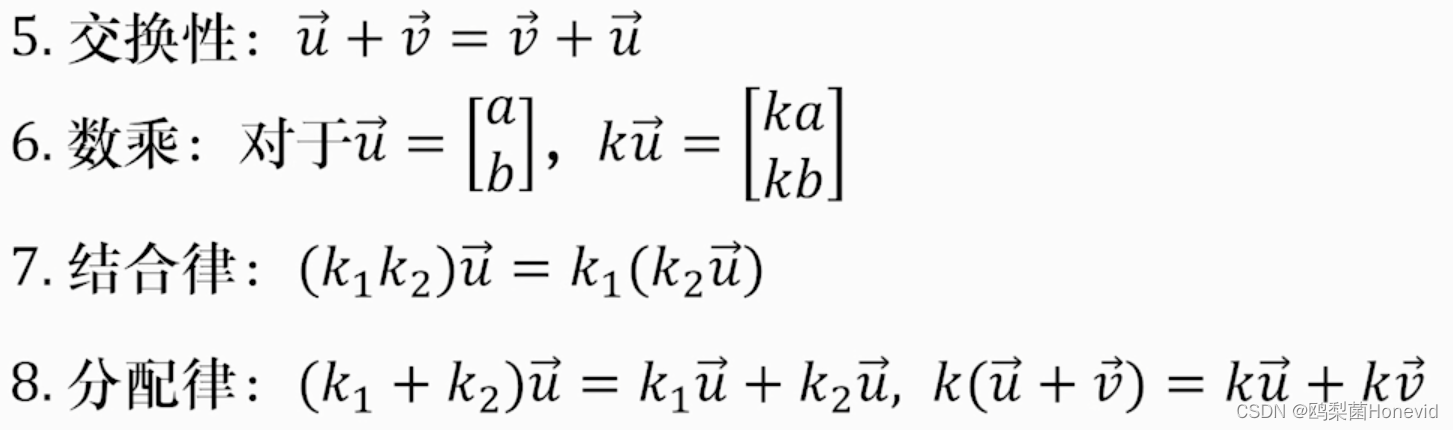
4. 复数简介


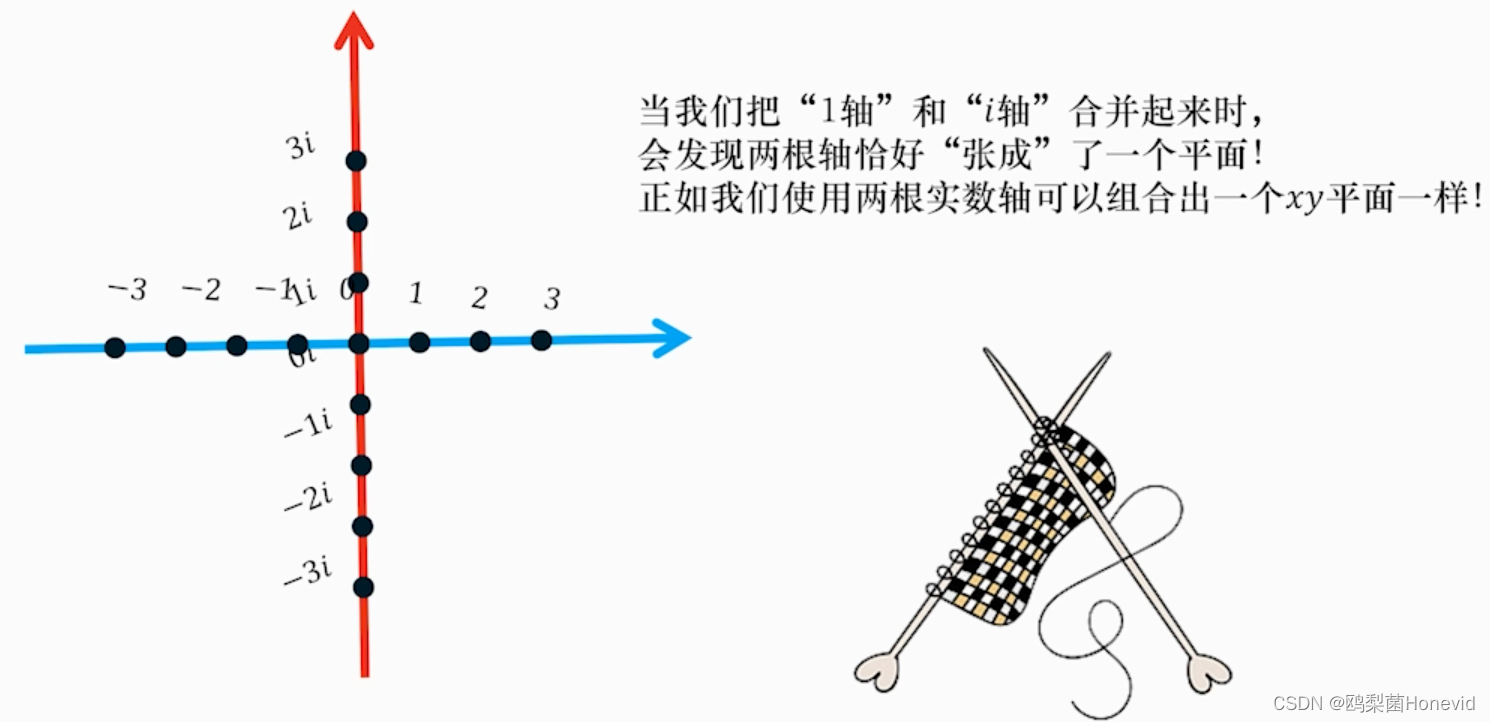
i轴和1轴的0处是同一个0,将他们连接起来构成一个平面!!!

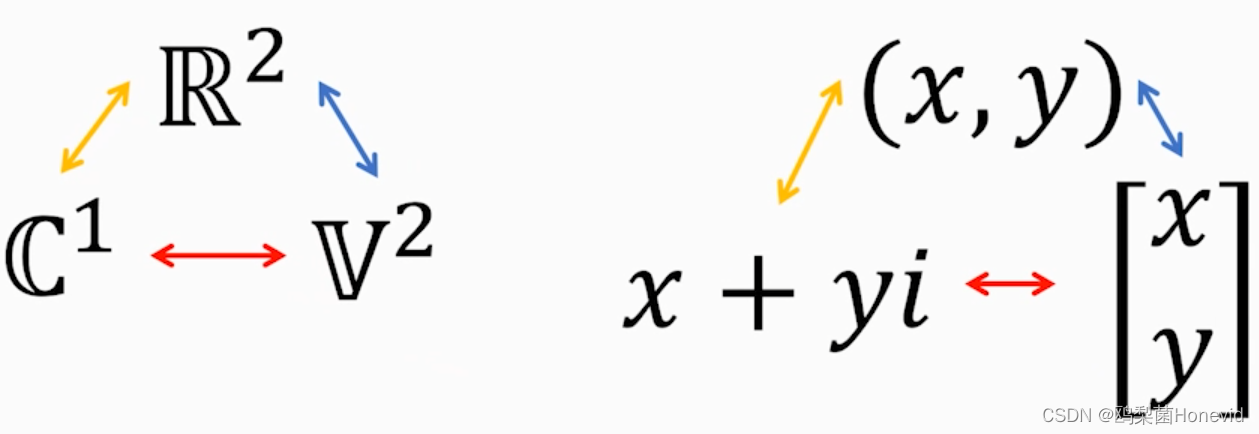
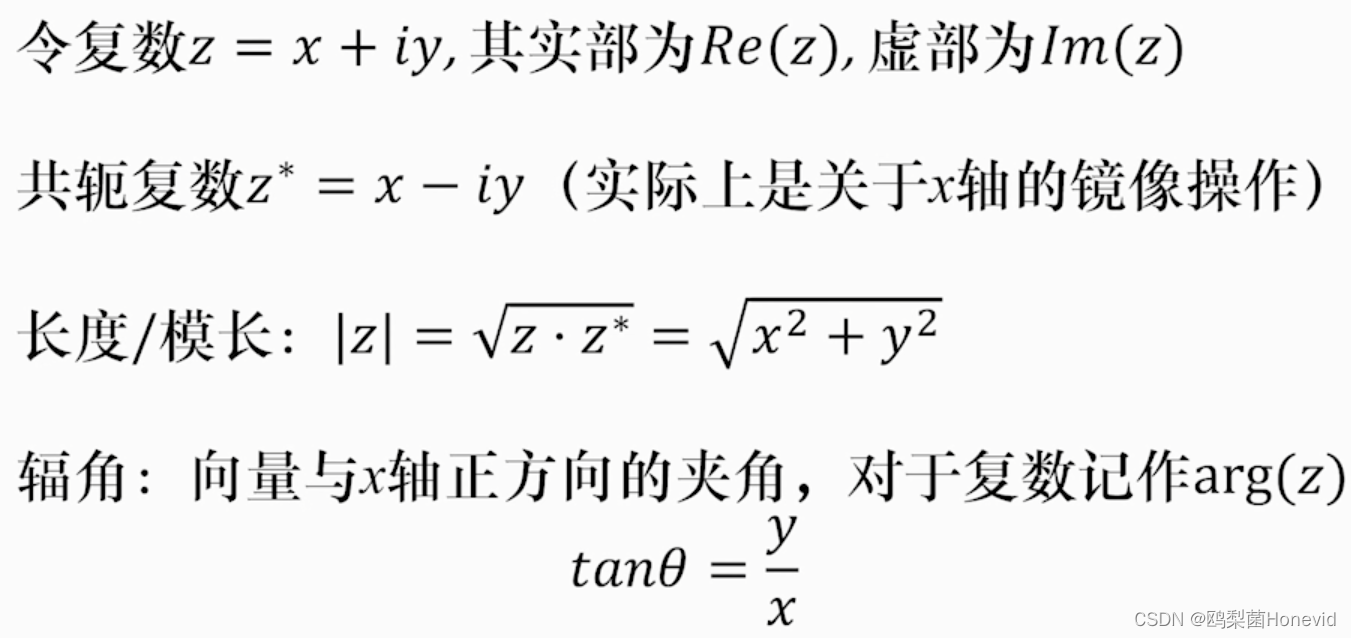
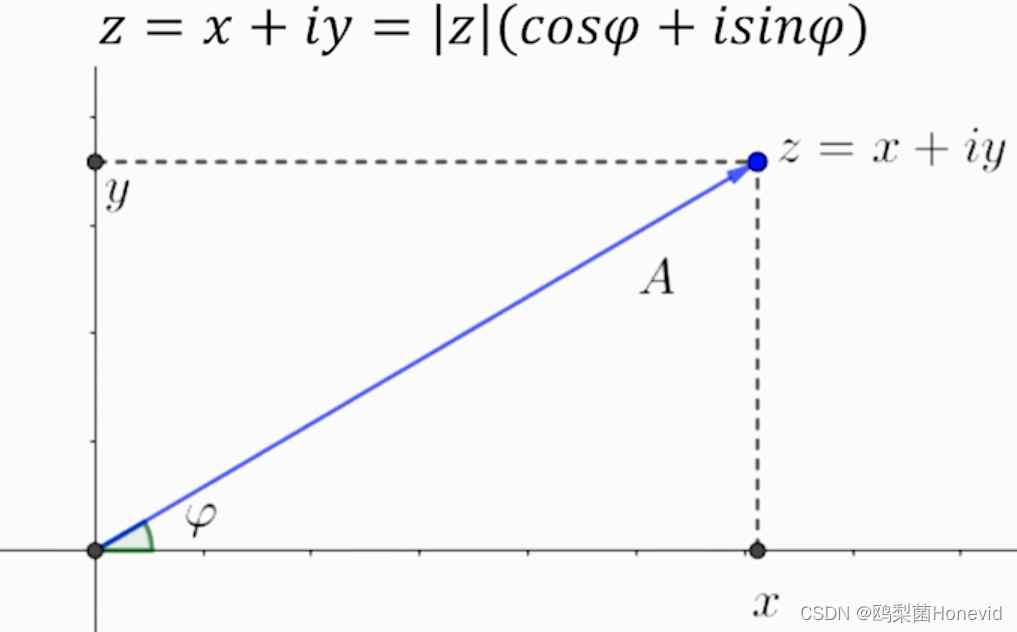
平面上表示
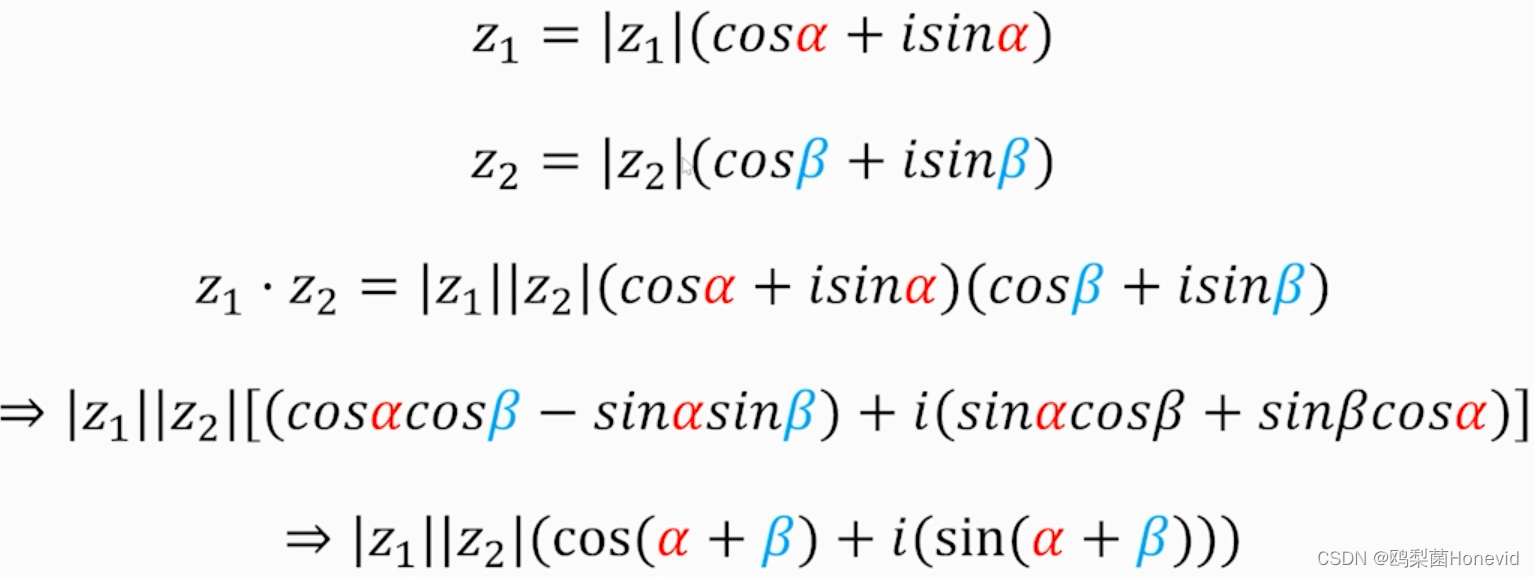
棣莫弗定理

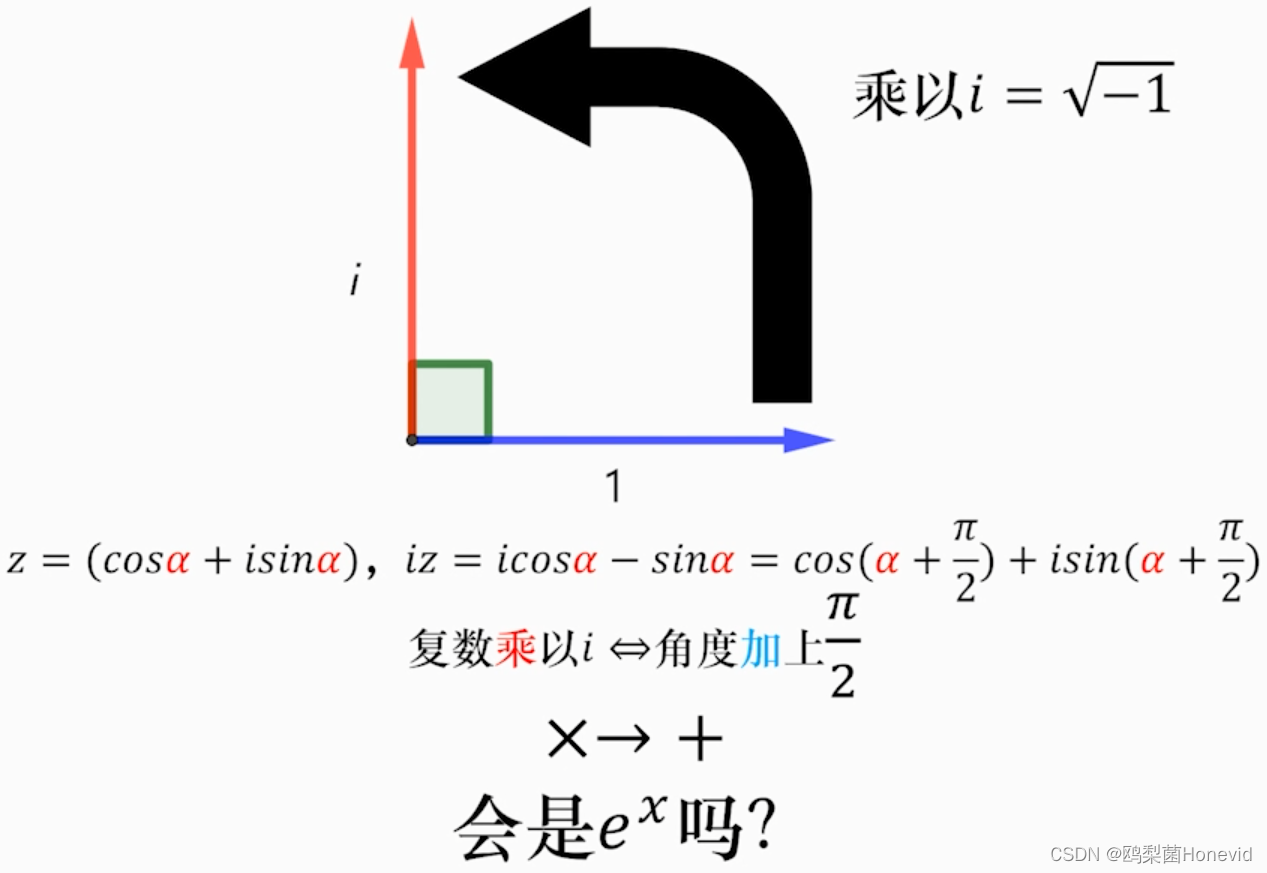
此处请联想到上述的同态映射,即: e x ∗ e y = e x + y e^x*e^y=e^{x+y} ex∗ey=ex+y,即 f ( x ) + f ( y ) = f ( x + y ) f(x)+f(y)=f(x+y) f(x)+f(y)=f(x+y),下面是通过python对猜想进行证实

作图
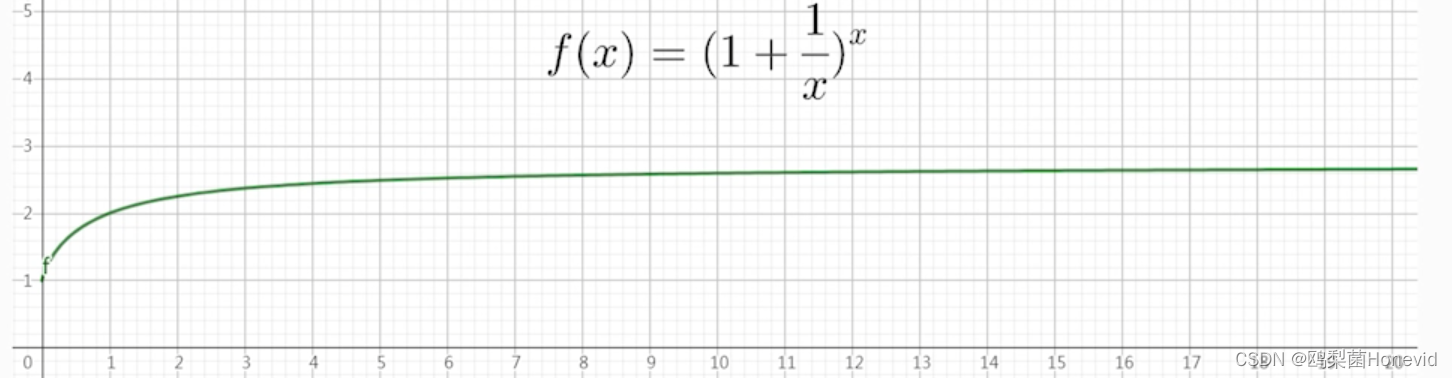
即:
lim n → ∞ ( 1 + 1 n ) n = e \begin{aligned}\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n&=e\end{aligned} n→∞lim(1+n1)n=e
lim n → ∞ ( 1 + a n ) n = [ lim n → ∞ ( 1 + a n ) n a ] a ⟶ t = n a [ lim t → ∞ ( 1 + 1 t ) t ] a = e a \lim_{n\to\infty}\left(1+\frac{\color{red}{a}}n\right)^n=\left[\lim_{n\to\infty}\left(1+\frac{\color{red}{a}}n\right)^{\color{red}{\frac{n}{a}}}\right]^a\overset{t=\frac na}{\operatorname*{\longrightarrow}}\left[\lim_{t\to\infty}\left(1+\frac1t\right)^t\right]^a=e^{\color{red}{a}} n→∞lim(1+na)n=[n→∞lim(1+na)an]a⟶t=an[t→∞lim(1+t1)t]a=ea
将a换成x,x也看作常数:
lim n → ∞ ( 1 + x n ) n = e x \lim_{n\to\infty}\left(1+\frac xn\right)^n=e^x n→∞lim(1+nx)n=ex
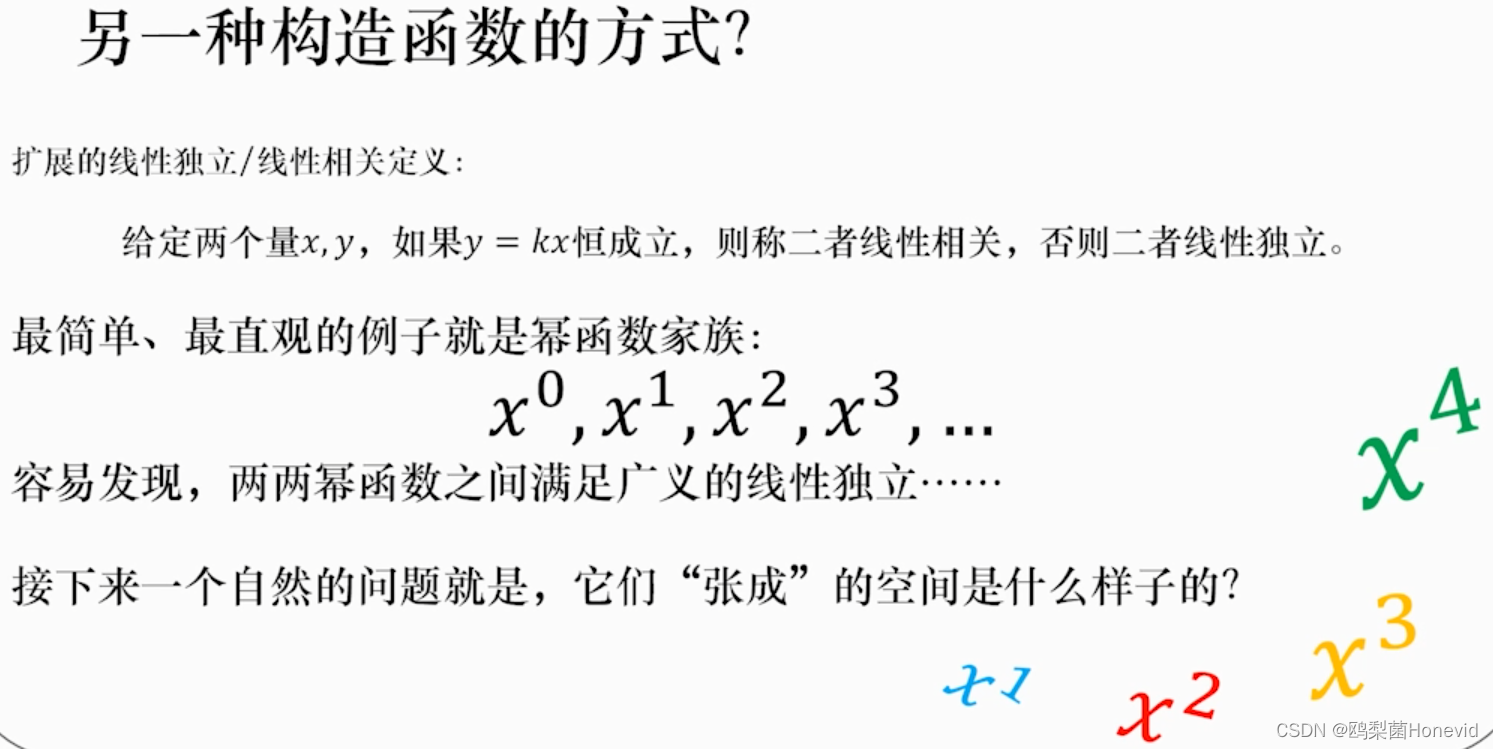
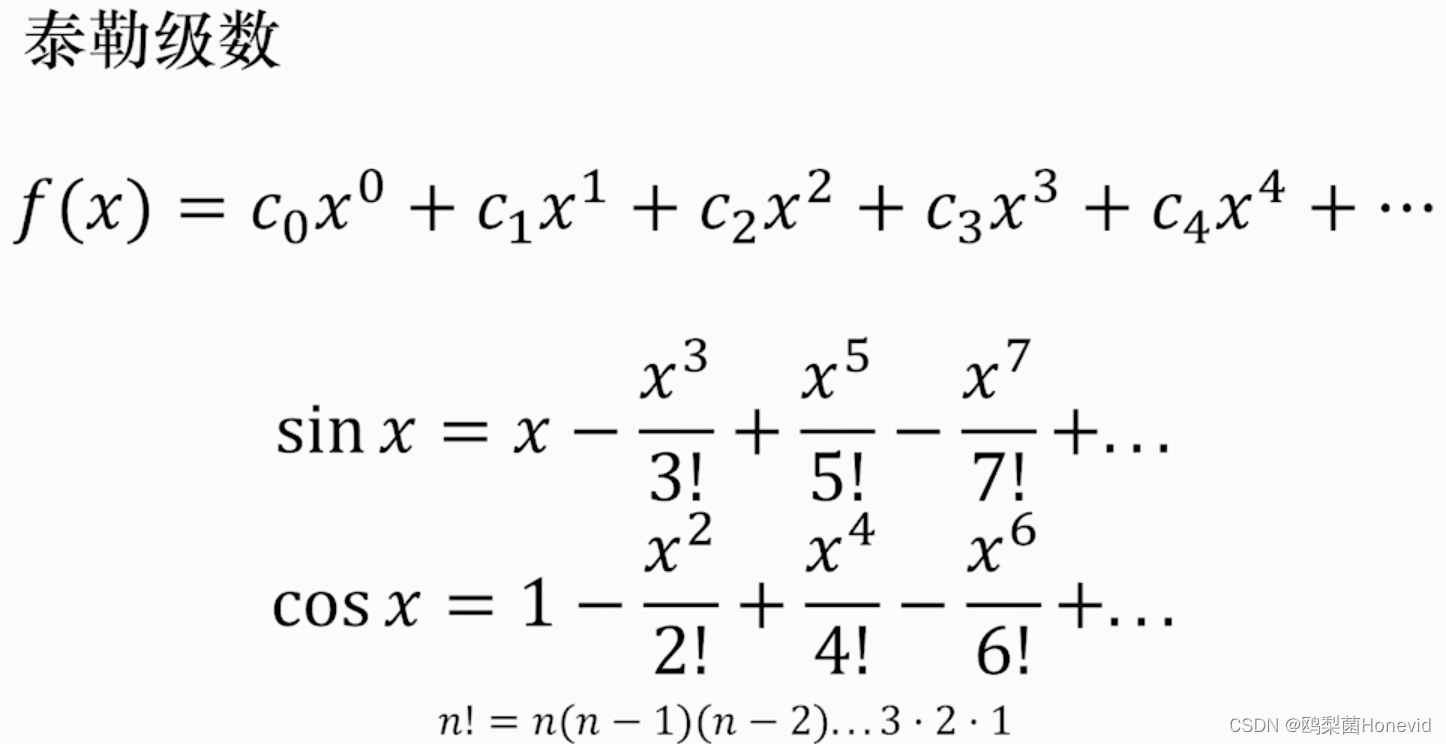
使用幂函数调整比例,从而张成新的函数
(看到这里我真的绷不住了,这个样子叫做零基础。。。还好我刚考过研,还记得些哈哈哈)
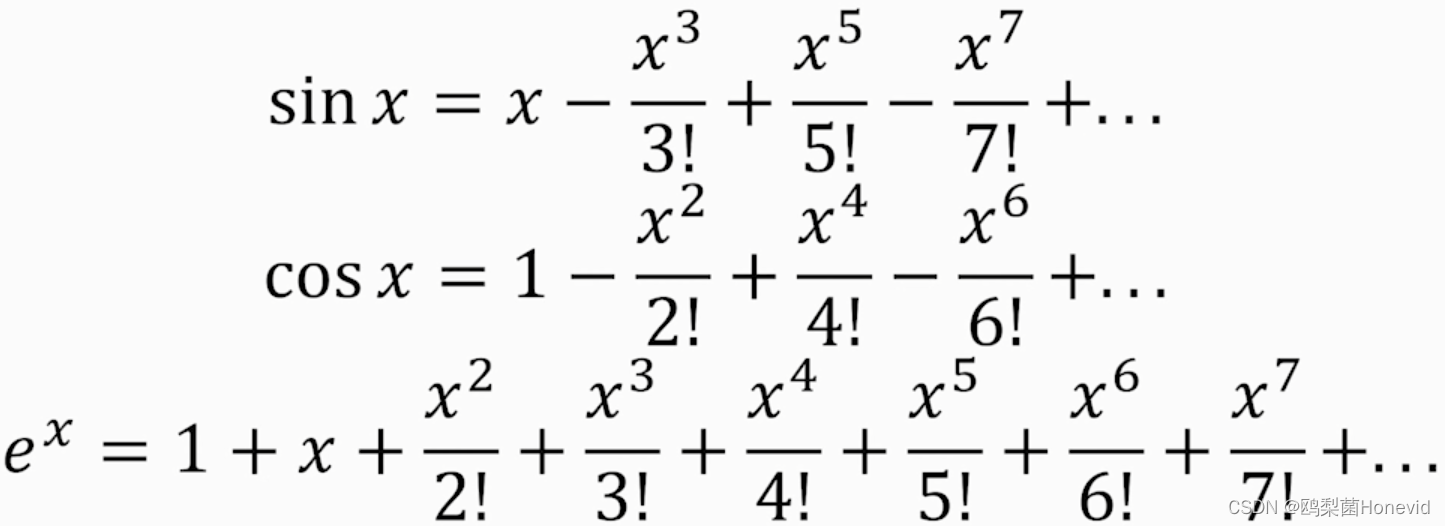
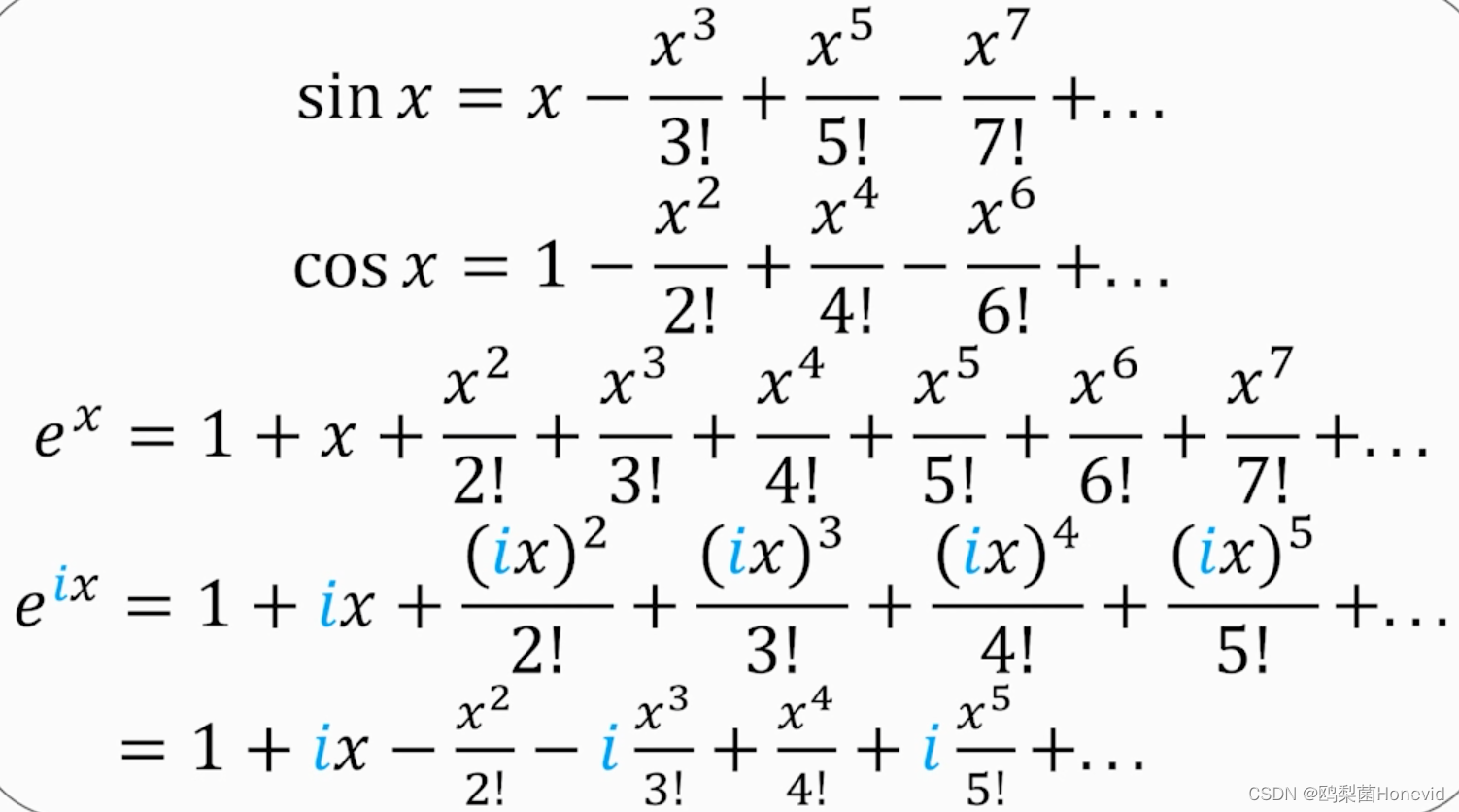
欧拉公式:
e i x = c o s x + i s i n x e^{ix}=cosx+isinx eix=cosx+isinx
从而有
z = r ( cos θ + i s i n θ ) = r e i θ z=r(\cos\theta+isin\theta)=re^{i\theta} z=r(cosθ+isinθ)=reiθ
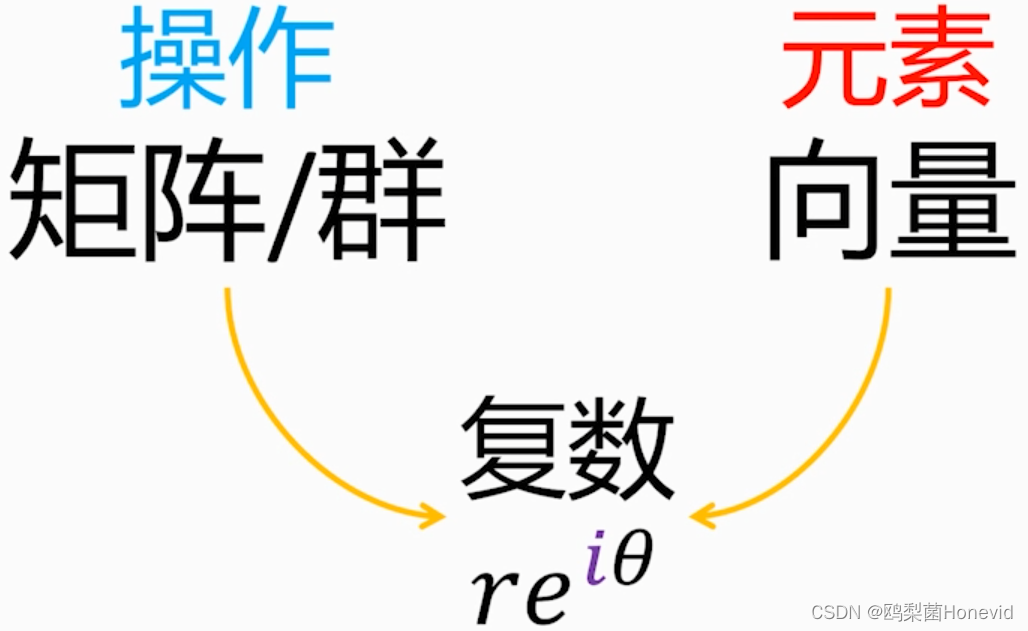


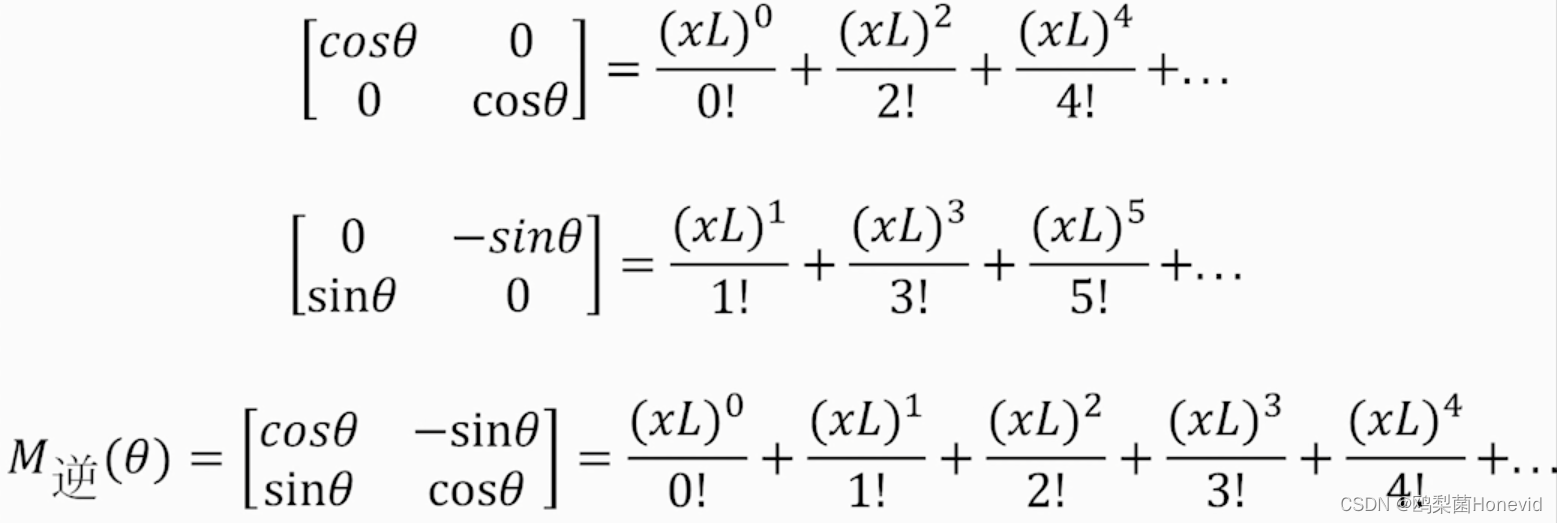
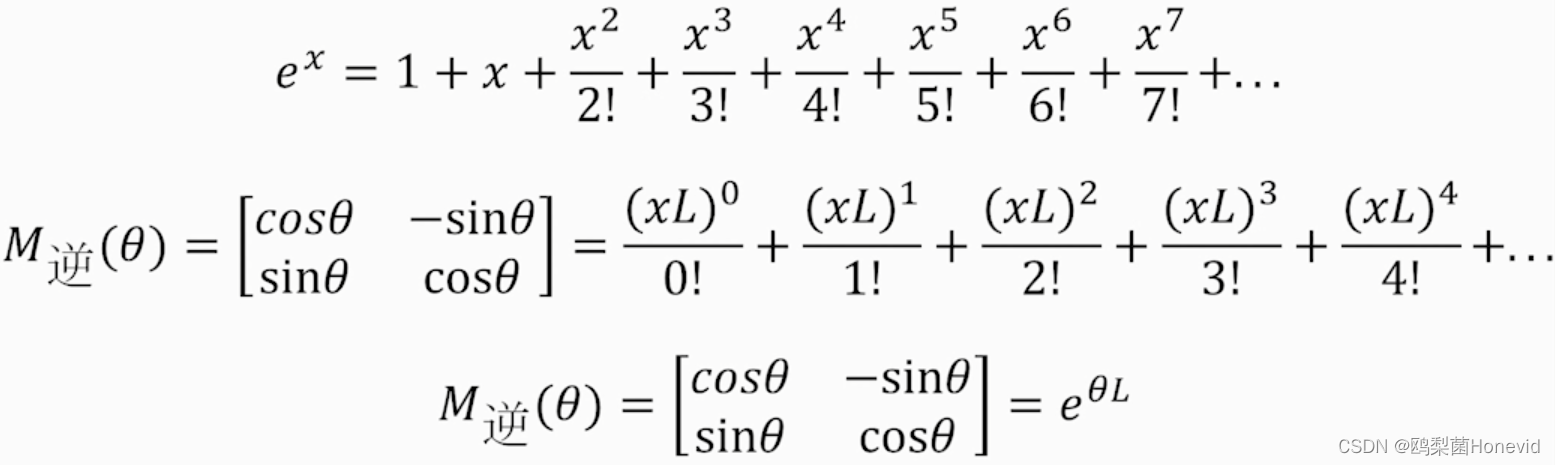
e L θ ν ⃗ ⇔ e^{L\theta}\vec{\nu}\Leftrightarrow eLθν⇔将 v ⃗ \vec{v} v逆时针转动角度 θ \theta θ
e i θ e^{i\theta} eiθ z ⇔ z\Leftrightarrow z⇔将 z z z逆时针转动角度 θ \theta θ

相关文章:

量子算法入门——2.线性代数与复数
参考资料: 【【零基础入门量子计算-第03讲】线性代数初步与复数】 来自b站up:溴锑锑跃迁 建议关注他的更多高质量文章:CSDN:【溴锑锑跃迁】 0. 前言 强烈建议搭配b站原视频进行观看,这只是我当时看的笔记,…...

分别通过select、多进程、多线程实现一个并发服务器
多进程 #include<myhead.h>#define PORT 8888 //端口号 #define IP "192.168.114.74" //IP地址//定义函数处理客户端信息 int deal_cli_msg(int newfd, struct sockaddr_in cin) {//5、收发数据使用newfd完成通信char buf[128] "&qu…...

如何在 emacs 上开始使用 Tree-Sitter (archlinux)
文章目录 如何在emacs上开始使用Tree-Sitter(archlinux) 如何在emacs上开始使用Tree-Sitter(archlinux) 在archlinux上使用比windows上不知道要方便多少倍! $ sudo pacman -S emacs $ sudo pacman -S tree-sitter这里…...

FL Studio2024最新中文版有哪些其新功能特点?
除了之前提到的特点外,FL Studio 21还有以下一些值得注意的特点: 高效的音频处理:FL Studio 21具备高效的音频处理能力,能够实时处理多轨道音频,提供低延迟的音频播放和录制,确保音乐制作过程中的流畅性和实…...
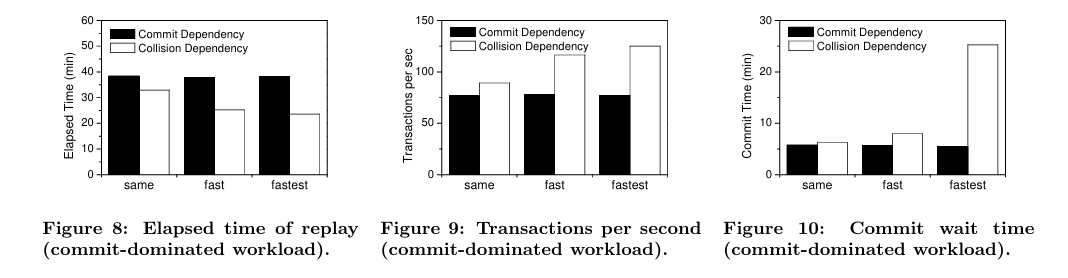
Oracle的学习心得和知识总结(三十二)|Oracle数据库数据库回放功能之论文四翻译及学习
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《Oracle Database SQL Language Reference》 2、参考书籍:《PostgreSQL中文手册》 3、EDB Postgres Advanced Server User Gui…...

系统架构27 - 软件架构设计(6)
基于架构的软件开发方法 基于架构的软件开发方法(ABSD)概述概念与术语开发模型体系结构需求体系结构设计体系结构文档化体系结构复审体系结构实现体系结构的演化 基于架构的软件开发方法(ABSD) 基于体系结构的软件设计 (Architec…...
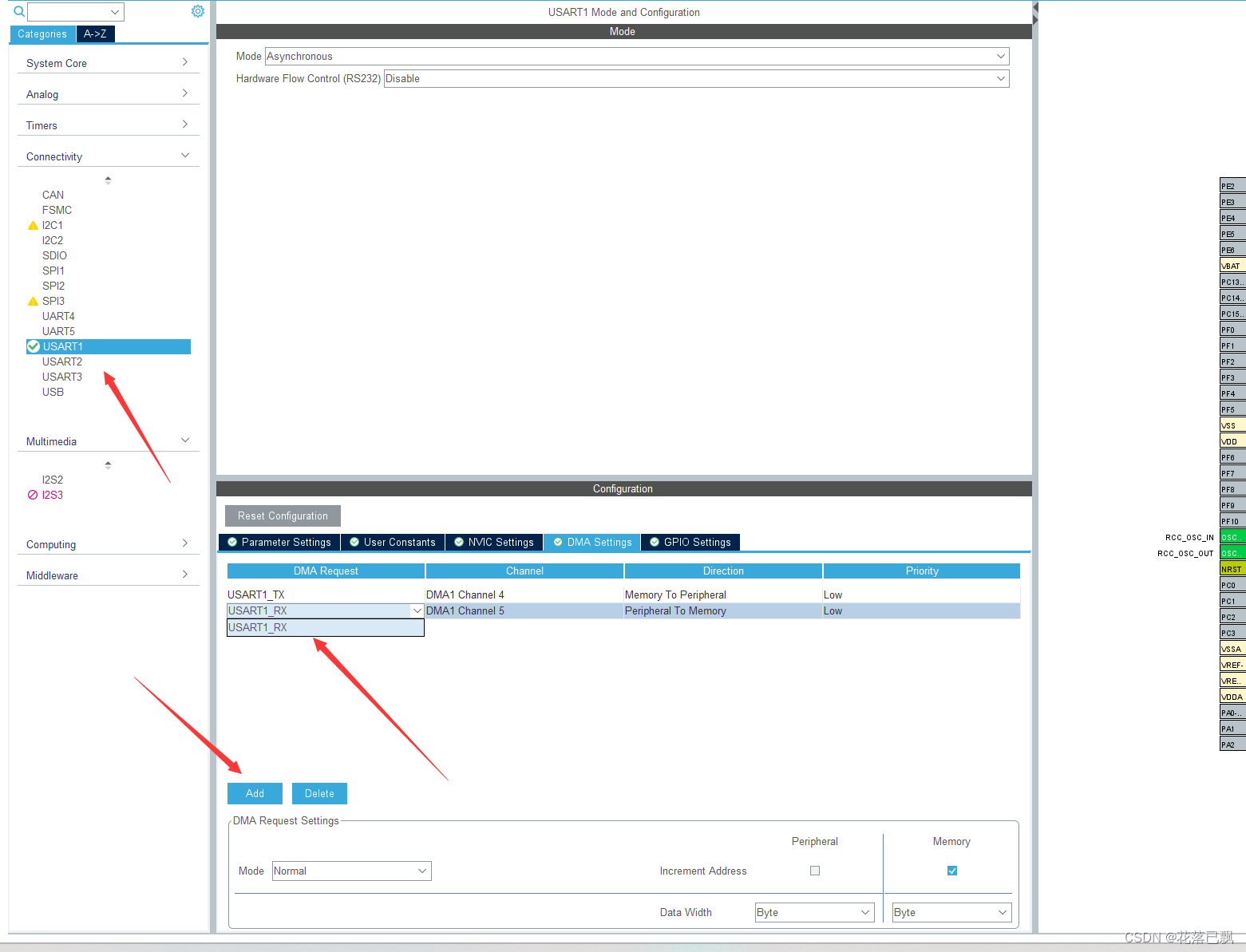
STM32 cubemx配置DMA+空闲中断接收不定长数据
文章目录 前言一、串口空闲中断二、DMA空闲中断接收不定长数据实现思路三、STM32Cubemx配置DMA空闲中断接收不定长数据四、代码编写总结 前言 本篇文章给大家讲解一下DMA串口空闲中断接收串口不定长数据,之前我们也是讲解过串口接收不定长数据的,那么本…...

Pycharm配置运行selenium教程
一、下载chrome浏览器和同版本的chromedriver chrome测试版版本120.0.6099.109 链接:https://pan.baidu.com/s/1pvFqL0WN8OkqPmURAs83kg?pwdvtsh 提取码:vtsh chromedriver版本120.0.6099.109 链接:https://pan.baidu.com/s/16fWWkrlD5C3J…...

银河麒麟V10开机后黑屏解决方法
情况描述: 单位的国产化电脑采用银河麒麟V10系统,在使用了近两个月时间后,开机到加载桌面那一步无法加载图形化桌面。 原理讲解 Linux本是纯命令行形式的系统,银河麒麟基于Linux中的Ubuntu LTS内核开发,其图形化的品牌…...

【Git版本控制 02】分支管理
目录 一、创建分支 二、切换分支 三、合并分支 四、删除分支 五、合并冲突 六、分支策略 七、bug分支 一、创建分支 # 当前仓库只有 master 一个主分支 # 可通过 git branch 是进行分支管理的命令,可通过不同参数对分支进行查看、创建、删除(base) [rootloc…...

基金分类
一、按基金运作方式分类 (一)封闭式基金 是基金份额总额在期限内固定不变,在期限内不可申购和赎回。 (二)开放式基金 是基金份额总额不固定,在期限内可以申购和赎回。 这里的开放式基金特指传统的开放式基…...
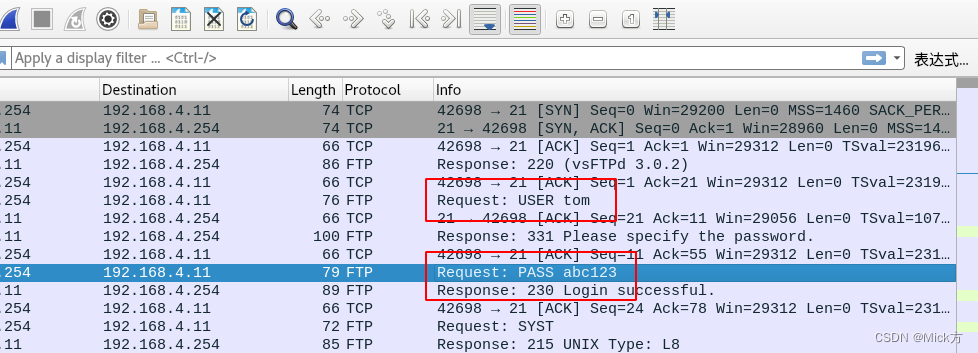
kali系统概述、nmap扫描应用、john破解密码、抓包概述、以太网帧结构、抓包应用、wireshark应用、nginx安全加固、Linux系统加固
目录 kali nmap扫描 使用john破解密码 抓包 封装与解封装 网络层数据包结构 TCP头部结构编辑 UDP头部结构 实施抓包 安全加固 nginx安全 防止缓冲区溢出 Linux加固 kali 实际上它就是一个预安装了很多安全工具的Debian Linux [rootmyhost ~]# kali resetkali …...
)
Spring Cloud 路由和消息传递 (HTTP 路由)
Spring Cloud 路由 Spring Cloud 路由是指将请求路由到特定服务的机制。Spring Cloud 提供了多种路由机制,包括: Ribbon: 一个基于 HTTP 和 TCP 的客户端负载均衡工具,提供软负载均衡、故障转移等功能。Feign: 一个声明式的 HTTP 客户端&am…...
【PyQt】12-滑块、计数控件
文章目录 前言一、滑块控件 QSlider运行结果 二、计数器控件 QSpinBox运行结果 总结 前言 1、滑块控件 2、计数控件 一、滑块控件 QSlider #Author :susocool #Creattime:2024/2/15 #FileName:28-滑块控件 #Description: 通过滑块选择字体大小 import sys from PyQ…...
【牛客面试必刷TOP101】Day21.BM11 链表相加(二)和BM12 单链表的排序
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:牛客面试必刷TOP101 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!&…...

疑似针对安全研究人员的窃密与勒索
前言 笔者在某国外开源样本沙箱平台闲逛的时候,发现了一个有趣的样本,该样本伪装成安全研究人员经常使用的某个渗透测试工具的破解版压缩包,对安全研究人员进行窃密与勒索双重攻击,这种双重攻击的方式也是勒索病毒黑客组织常用的…...

Mamba-UNet:用于医学图像分割的类似UNet的纯视觉Mamba网络
摘要 在医学图像分析的最新进展中,卷积神经网络(CNN)和视觉转换器(ViT)都取得了显著的基准成绩。前者通过其卷积操作在捕获局部特征方面表现出色,而后者则通过利用自注意力机制实现了出色的全局上下文理解。然而,这两种架构在有效建模医学图像中的长距离依赖关系时都存…...

2024/2/14
1.1、若有下面的变量定义,以下语句中合法的是( A )。 int i,a[10],*p; A) pa2; B) pa[5]; C) pa[2]2; D) p&(i2); 1.2、有以下程序 …...
跟廖雪峰老师学习Git(持续更新)
Git简介 创建版本库 第一步,创建一个新目录 第二步,通过git init变成Git可以管理的仓库 把文件添加到文本库,不要使用Windows自带的记事本! 我用的是VS code 创建readme.txt 放入库中 commit可以一次提交很多文件࿰…...

2024,欢迎来到性价比时代
「不是XX买不起,而是YY更有性价比。」——翻开过去一年的商业消费史,这句话几乎可以贯穿始终。年轻消费者们追求性价比的眼光一旦定型,一些品牌过去被品质生活、消费升级包装出来的华丽外壳,很容易一击就碎。 胜出的「性价比之王…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
