DS:二叉树的链式结构及实现
创作不易,友友们给个三连吧!!
一、前言
前期我们解释过二叉树的顺序结构(堆)为什么比较适用于完全二叉树,因为如果用数组来实现非完全二叉树,那么数组的中间部分就可能会存在大量的空间浪费。
而二叉树的链式结构即用链表结构来存储二叉树,这里就没有什么限制了,所有的二叉树都可以用链式结构来存储,因为链式结构存在两个指针分别指向自己的左右孩子,无论是少了左孩子还是少了右孩子,只需要让相应的指针指向NULL就可以了。
虽然链式结构可以表示所有类型的二叉树,但是由于二叉树本身存储数据的价值并不大(链表、顺序表远远优于二叉树),所以实现增删查改是没有太大意义的,学习链式二叉树真正的意义是学会如何去控制、遍历二叉树的结构,为我们后期学习搜索二叉树做好铺垫。而以下的学习中要重点理解二叉树中的递归思想和分治思想 !
二、链式二叉树的实现
2.1 节点结构体的创建
创建的方式和单链表的很相似,唯一的区别就是要有两个指针,一个指向自己的左孩子,一个指向自己的右孩子!
typedef int BTDataType;//方便我们后面要存储其他类型的数据的时候方便修改!
typedef struct BinaryTreeNode
{BTDataType data;//二叉树节点的数据域struct BinaryTreeNode* left;//左孩子struct BinaryTreeNode* right;//右孩子
}BTNode;
2.2 二叉树节点的创建
二叉树节点构建方式和单链表节点的构建方式相同!
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL)//如果创建不成功{perror("malloc fail");exit(1);}//如果创建成功newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}2.3 前序遍历
为了能够深入前中后续遍历,我们先手动创建一个二叉树,后面都按照这个二叉树来研究
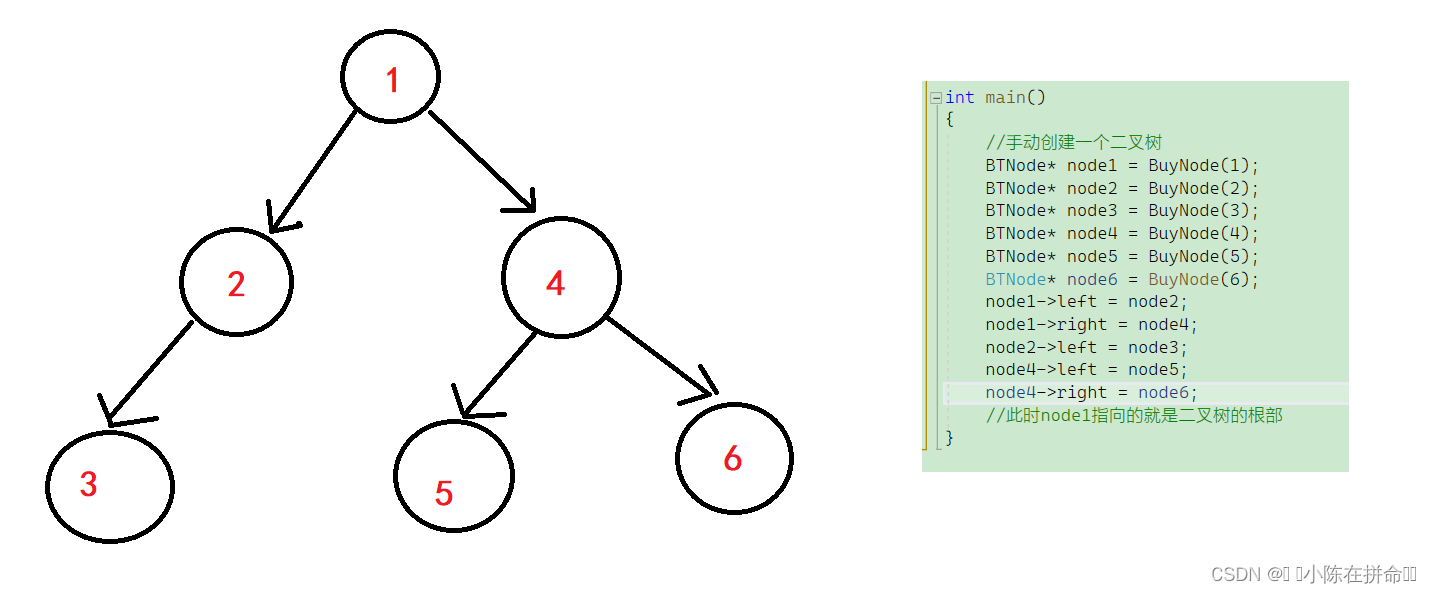
下面我先给出前中后续的遍历结果,再逐个分析,要注意,没有箭头默认指向空!
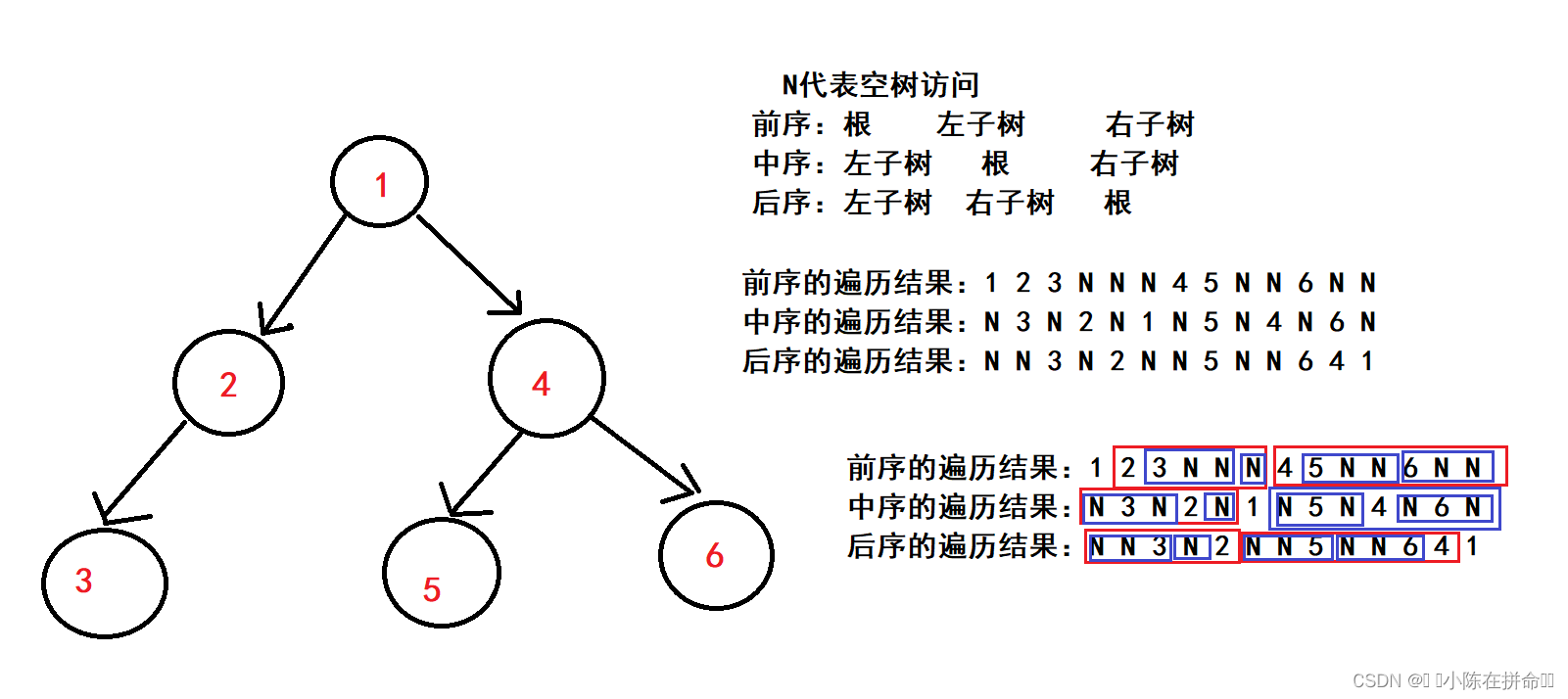
分析前序:
前序的顺序是根、左子树、右子树:首先1是根,接着访问1的左子树2,2也是根,再访问2的左子树3,3也是根,再访问3的左子树N,接着访问3的右子树N,,回归到2,对于2来说,他的左子树已经访问完了,然后访问右子树N,回归1,对于1来说,他的左子树已经访问完了,该访问他的右子树4了,4是根,接着访问4的左子树5,5也是根,接着访问5的左子树N,再访问5的右子树N,然后回归5,对于4来说,左子树访问完了,接着访问6,6的左子树是N,然后访问6的右子树N。此时所有节点都访问完了。
大家可以看看上面的图我画的框框,1这个根右边的2 3 N N N 和4 5 N N 6 N N 分别表示1的左右子树,而对于2这个根来说,3 N N 和 N分别代表2的左右子树,对于4这个根来说,5 N N和6 N N分别代表4的左右子树,对于3、5、6 这三个根来说,他们的左右子树都是N和N。
那么怎么写前序遍历的代码呢?根据上一段的思路我们可以发现,对于根1来说,他的左子树是以2为根的树,他的右子树是以4为根的树,而对于2来说,他的左子树是以3为根的树,右子树是N,对于4来说,他的左子树是以5为根的树,他的右子树是以6为根的树, 而对于3、5、6来说,他们其实也是根,左右子树都是N。所以将问题转化为递归问题。
void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}画一下递归展开图:
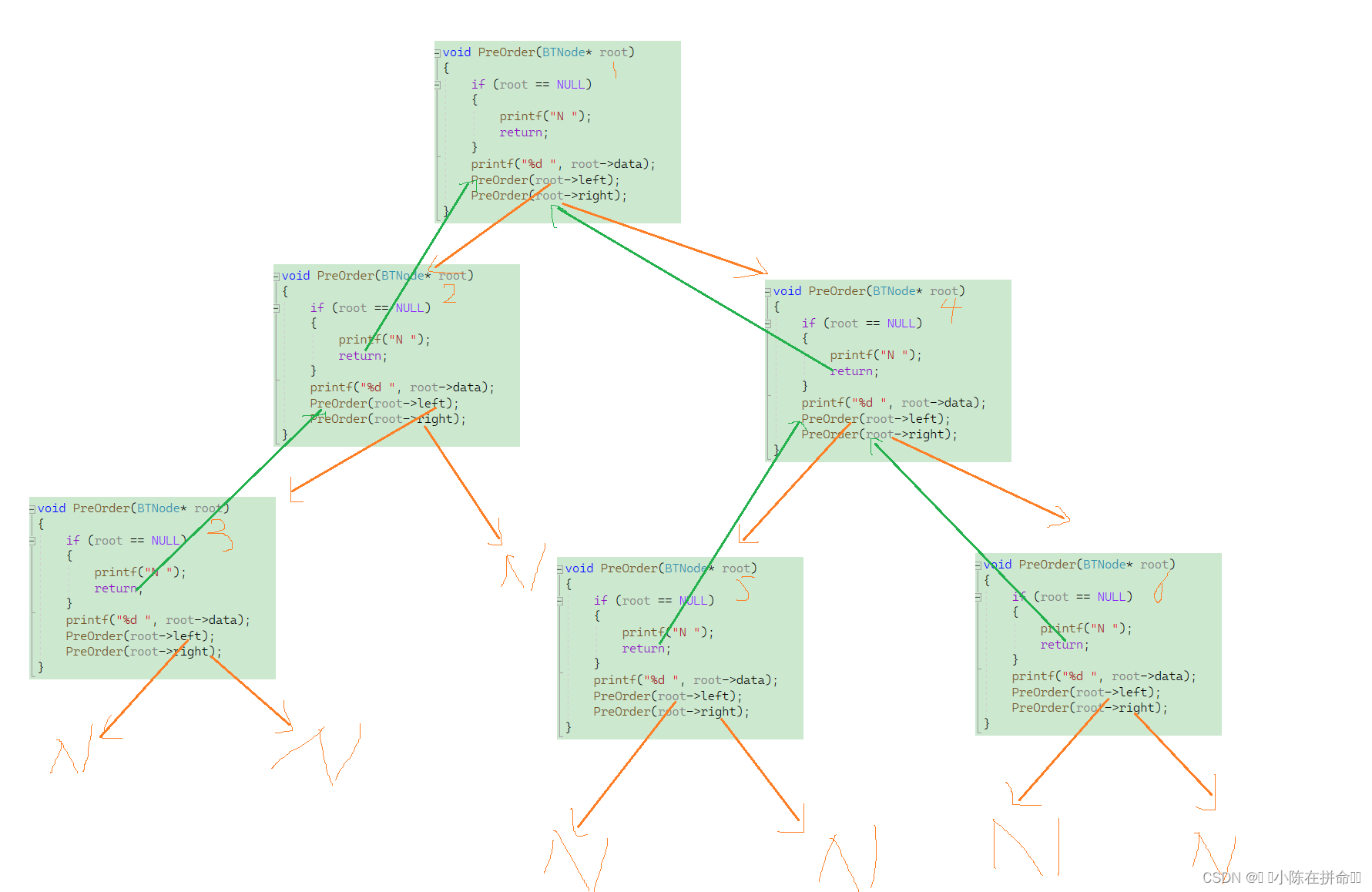
时间复杂度是O(N) 因为每个节点都遍历了一次
空间复杂度也是O(h) 通过上图可以看出,当开辟h个的函数栈帧后,后续的空间都是在前一个空间释放后复用的,所以最多同时只有h个栈帧空间被开辟,根据空间可以重复利用的特点,空间复杂度是o(N)!
中序遍历和后序遍历的方法是一样的,后面就不分析了
2.4 中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}2.5 后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}2.6 层序遍历
层序遍历是一层一层遍历,之前无论是前序、中序、还是后序遍历,都是根据父子关系(父亲会指向自己的左右孩子)转化成递归问题去遍历的, 但是链式二叉树的指针指向并不指向兄弟节点,所以这边如果要一层一层遍历,需要用到队列。
选择队列的原因是利用队列队头出队尾进的特点,下面进行分析:
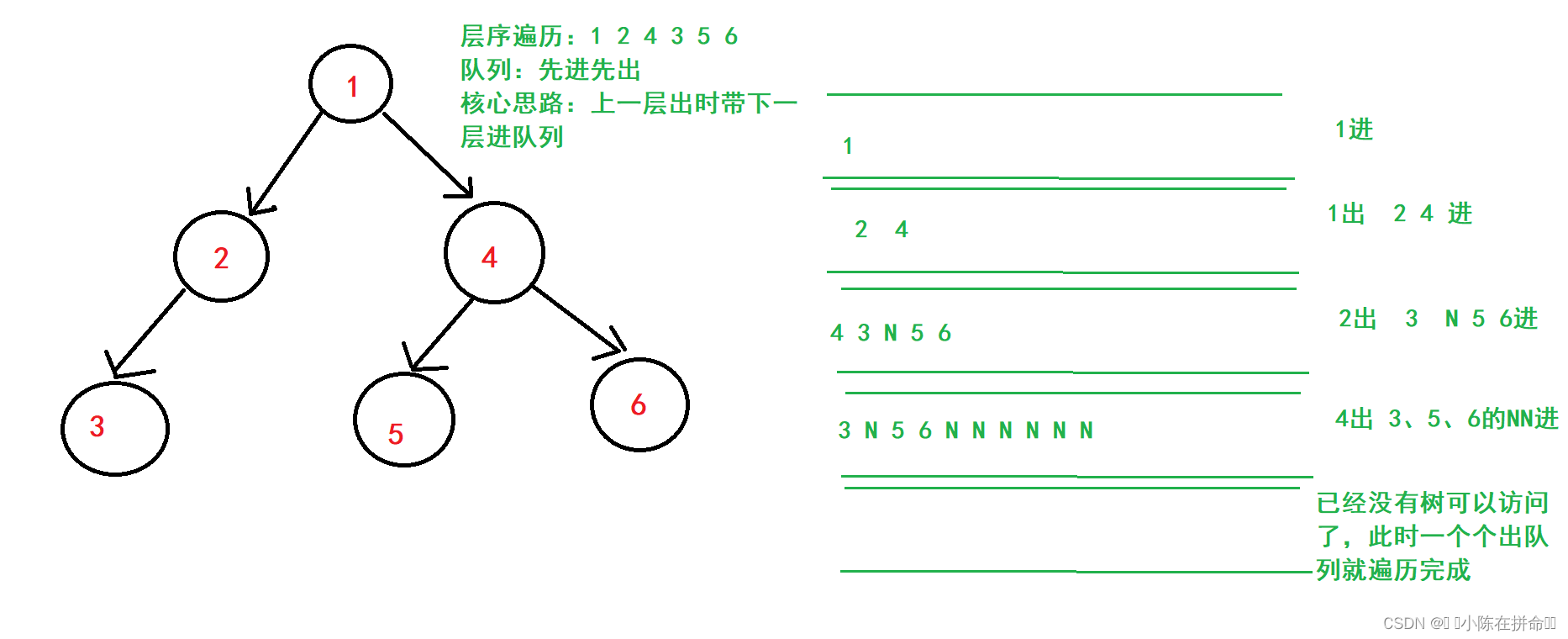
Queue.h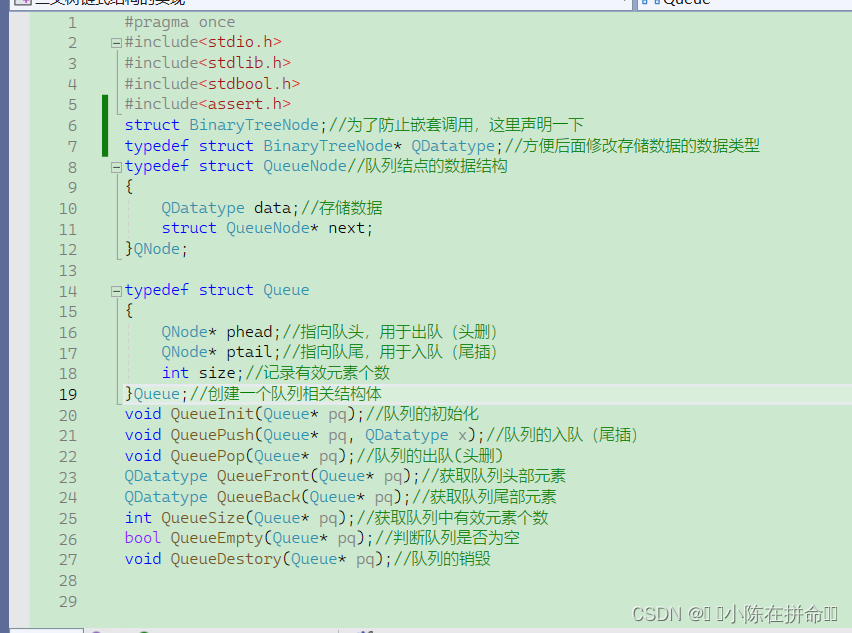
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)//如果不为NULL,就进队列QueuePush(&q, root);while (!QueueEmpty(&q))//队列为空,就是遍历完成{BTNode* front = QueueFront(&q);//让每一次循环过来的节点变成根部,再去访问左右子树QueuePop(&q);//记录完一个元素就出队列printf("%d ", front->data);if(front->left)QueuePush(&q, front->left);//左节点不为空,进队列if (front->right)QueuePush(&q, front->right);//右节点不为空,进队列}printf("\n");//遍历完了就可以销毁队列了QueueDestory(&q);
}2.7 二叉树节点个数

我们先按照按照军棋里的模式来解释分治思想:
假设军长要统计总人数,有两个方法,一个是军长一级一级去视察数人,这显然是效率比较低的, 而另一个方法就是分而治之——利用自己的职权将任务移交给下级,军长把任务分配给两个旅长,然后旅长统计过来的人数加上自己就是全军人数,旅长又分配给连长,将两个连长统计的人数加上自己就是全旅人数,以此类推……
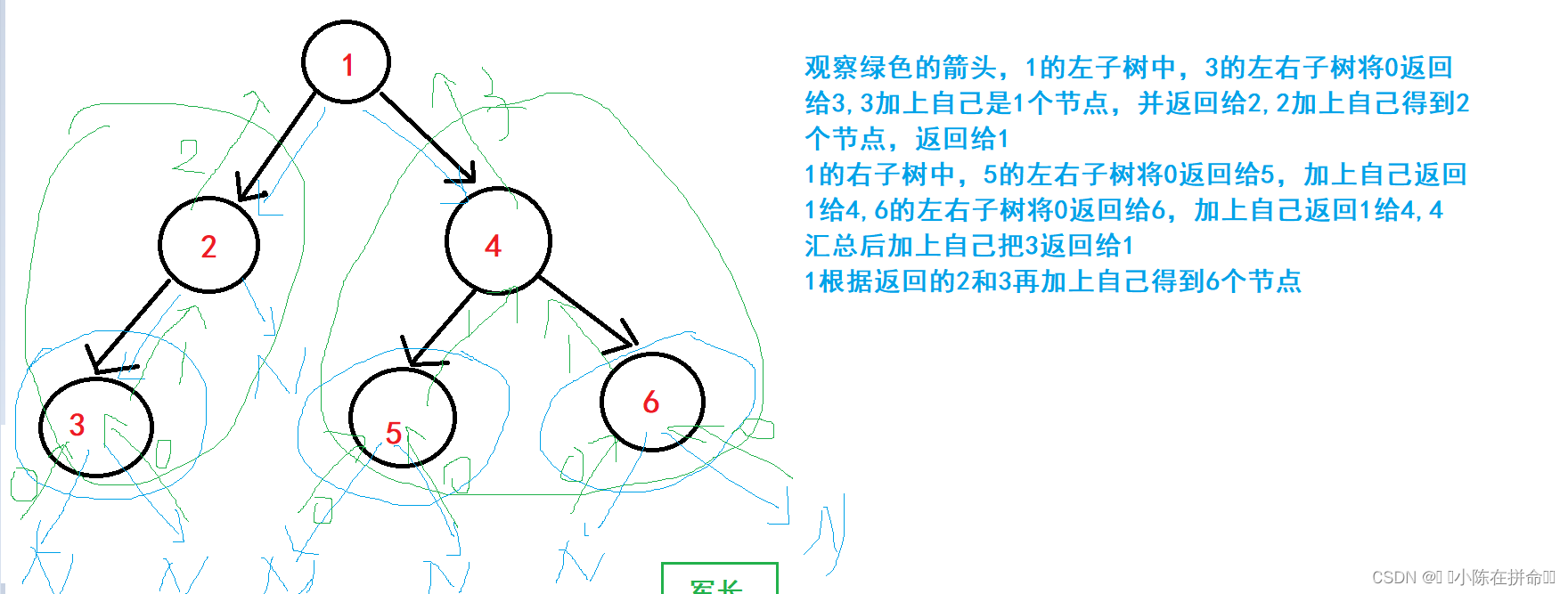
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}2.8 二叉树叶子节点个数
还是利用分治思想,叶子节点的特征是左右子树都为NULL,我们还是按照分治思想将这个任务拆分下去
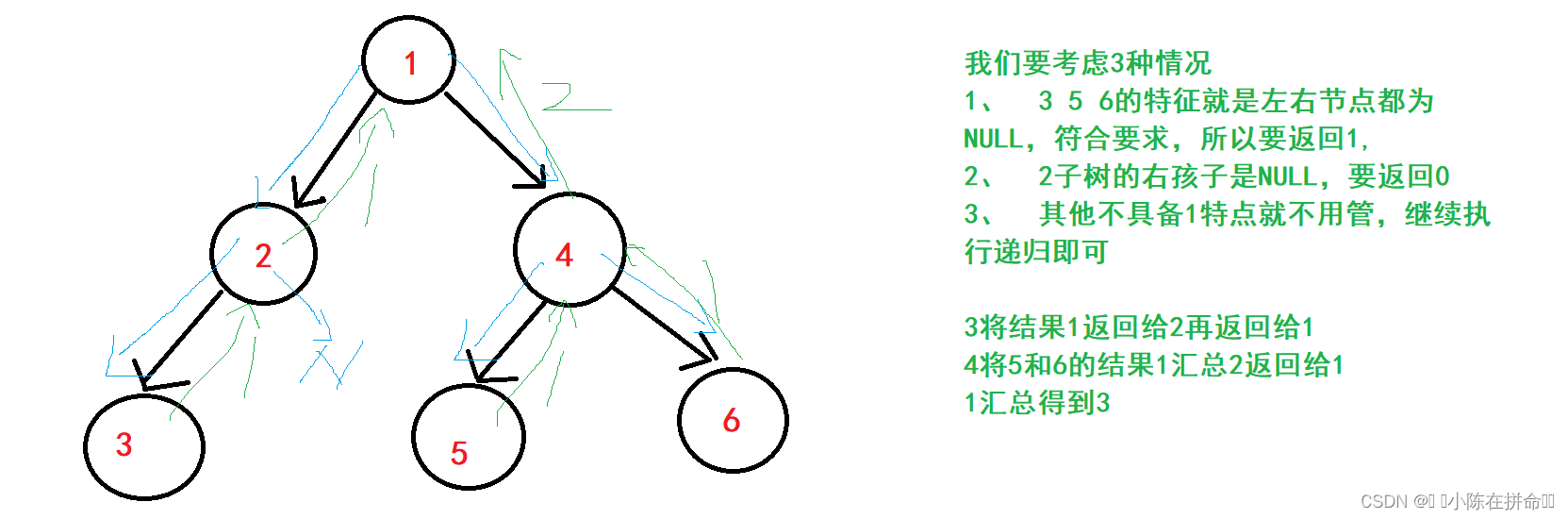
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}2.9 二叉树第k层节点
还是利用分治思想,将求第k层节点转化为求左子树的k-1层节点加上右子树的k-1层节点。
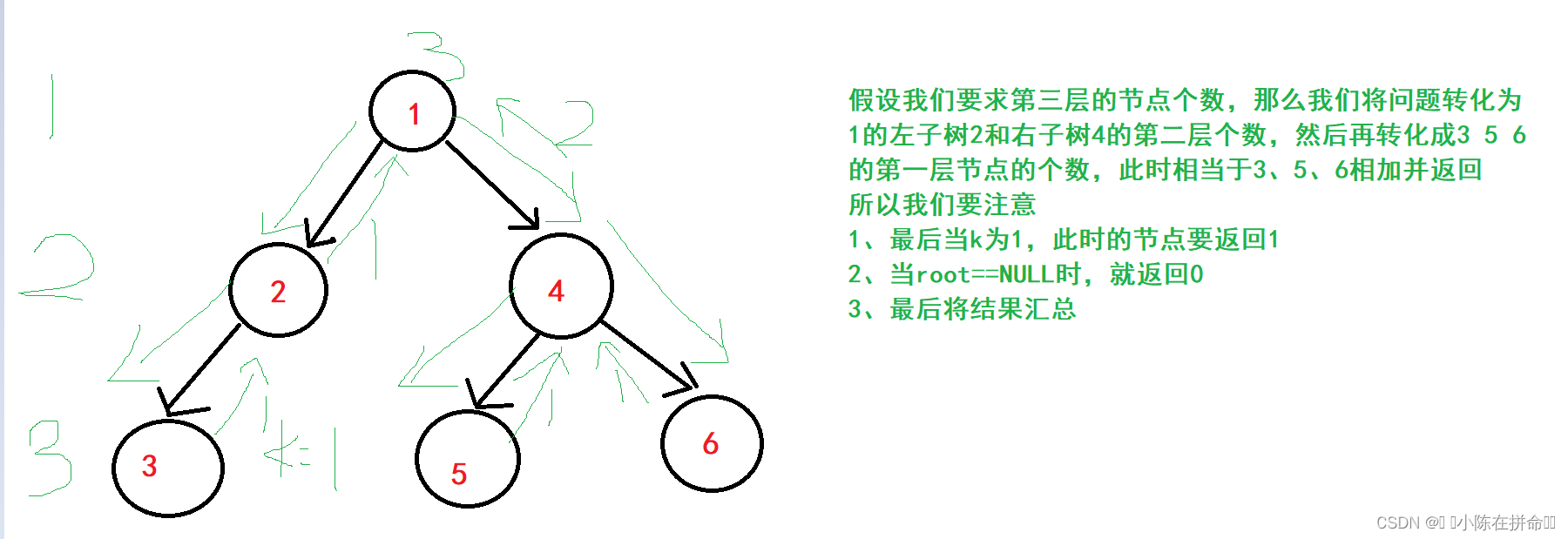
int BinaryTreeLevelKSize(BTNode* root,int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left,k-1) + BinaryTreeLevelKSize(root->right,k-1);
}2.10 二叉树的高度
还是利用分治思想,求高度转化为比较左右子树的大小再+1

int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeHeight(root->left) > BinaryTreeHeight(root->right) ? BinaryTreeHeight(root->left) + 1 : BinaryTreeHeight(root->right) + 1;
}其实这样写是有问题的!!!因为每次我递归比较完后,并没有记录最大值,所以导致每次递归的时候最大值都得再重新递归一次!!如果树节点高度特别高的话,就很可能会出现这样的问题。
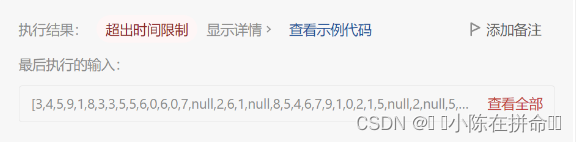
改进版:
int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;int LeftHeight = BinaryTreeHeight(root->left);int RightHeight = BinaryTreeHeight(root->right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}
所以我们在递归时使用三目表达式要注意:如果比较的过程已经递归一次了,比较的结果就不要再去递归了!!可以及时的记录值!!
2.11 二叉树查找值为x的节点
还是利用分治思想,转化为在左子树和右子树中找
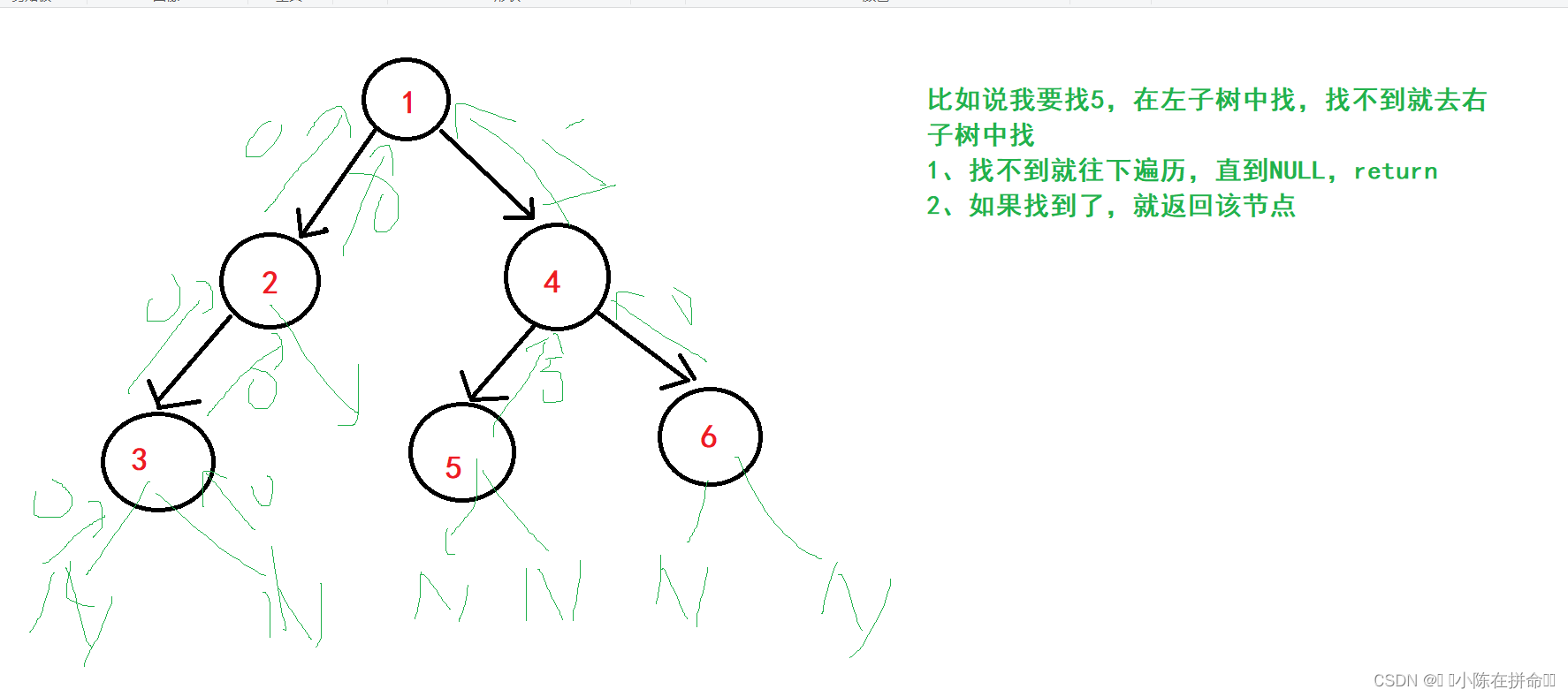
BTNode* BTFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* ret1 = BTFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = BTFind(root->right, x);if (ret2)return ret2;return NULL;
}2.12 通过前序遍历数组构建二叉树
之前我们构建二叉树是一个节点一个节点去手动连接,这次我们尝试自己利用前序遍历数组去构建二叉树,比如abc##de#g##f###

BTNode* BTCreate(char*arr,int*pi)
{if (arr[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BuyNode(arr[*pi]);(*pi)++;root->left = BTCreate(arr, pi);root->right = BTCreate(arr, pi);return root;
}递归展开图:
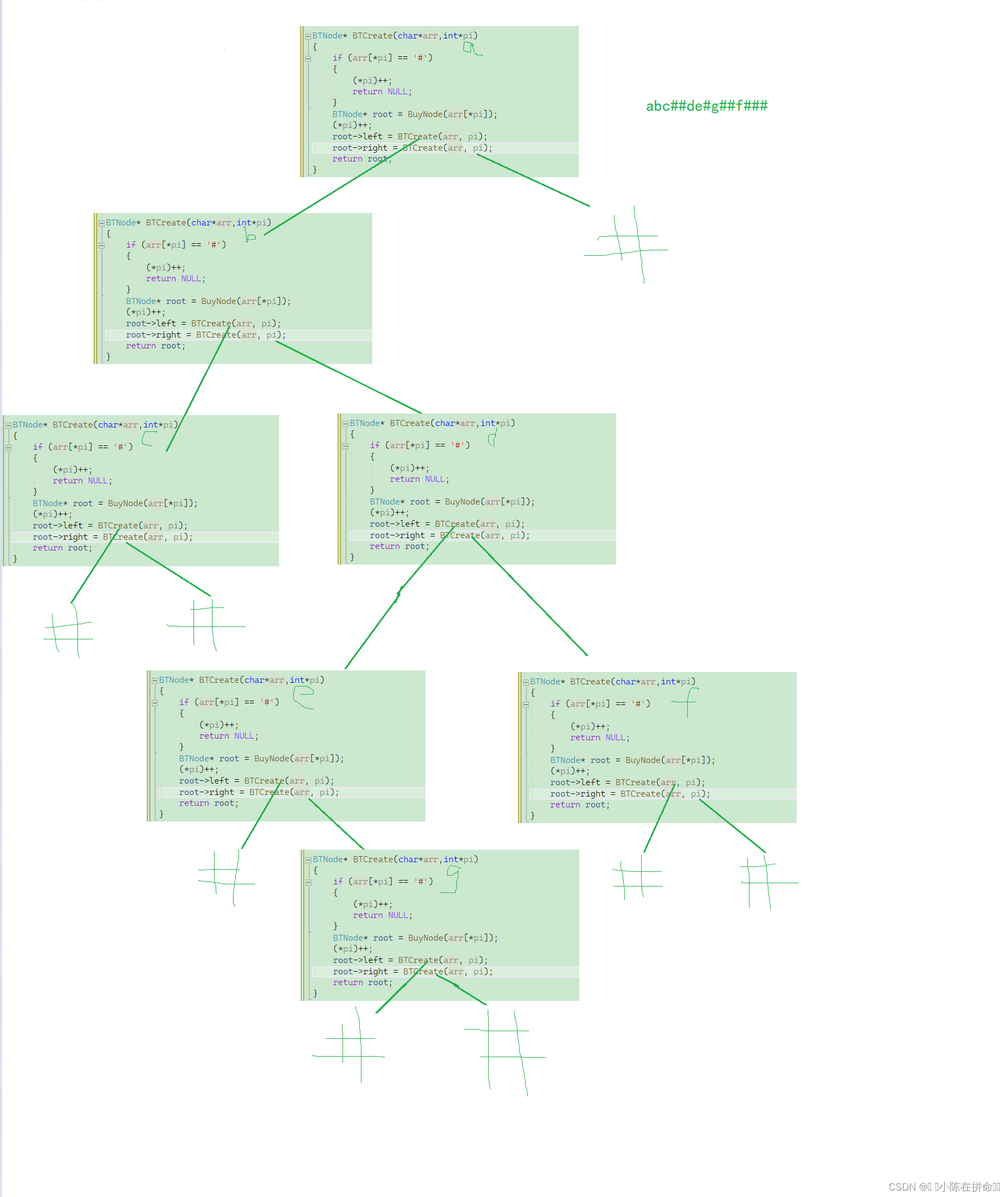
2.13 二叉树销毁
二叉树要销毁,就要遍历每个节点,因为我们如果先销毁根,那么就很可能找不到他的左子树和右子树了,除非销毁根之前记录一下,但是这样比较麻烦,所以我们选择后序遍历,先销毁左子树,再销毁右子树,再销毁根。
void BTDestory(BTNode* root)
{if (root == NULL)return;BTDestory(root->left);BTDestory(root->right);free(root);//root = NULL;没用
}注意:这里的参数是一级指针,而root本身也是指针,所以在这里对root置NULL,是没有意义的,所以要使用的话,要在main函数中手动置空(这里不用二级指针的原因是为了保持接口一致性)!!
2.14 判断二叉树是否是完全二叉树
完全二叉树的特点就是:前h-1层是满的,最后一层从前往后要到最后才会访问到NULL,所以们可以分析一下他的特点:
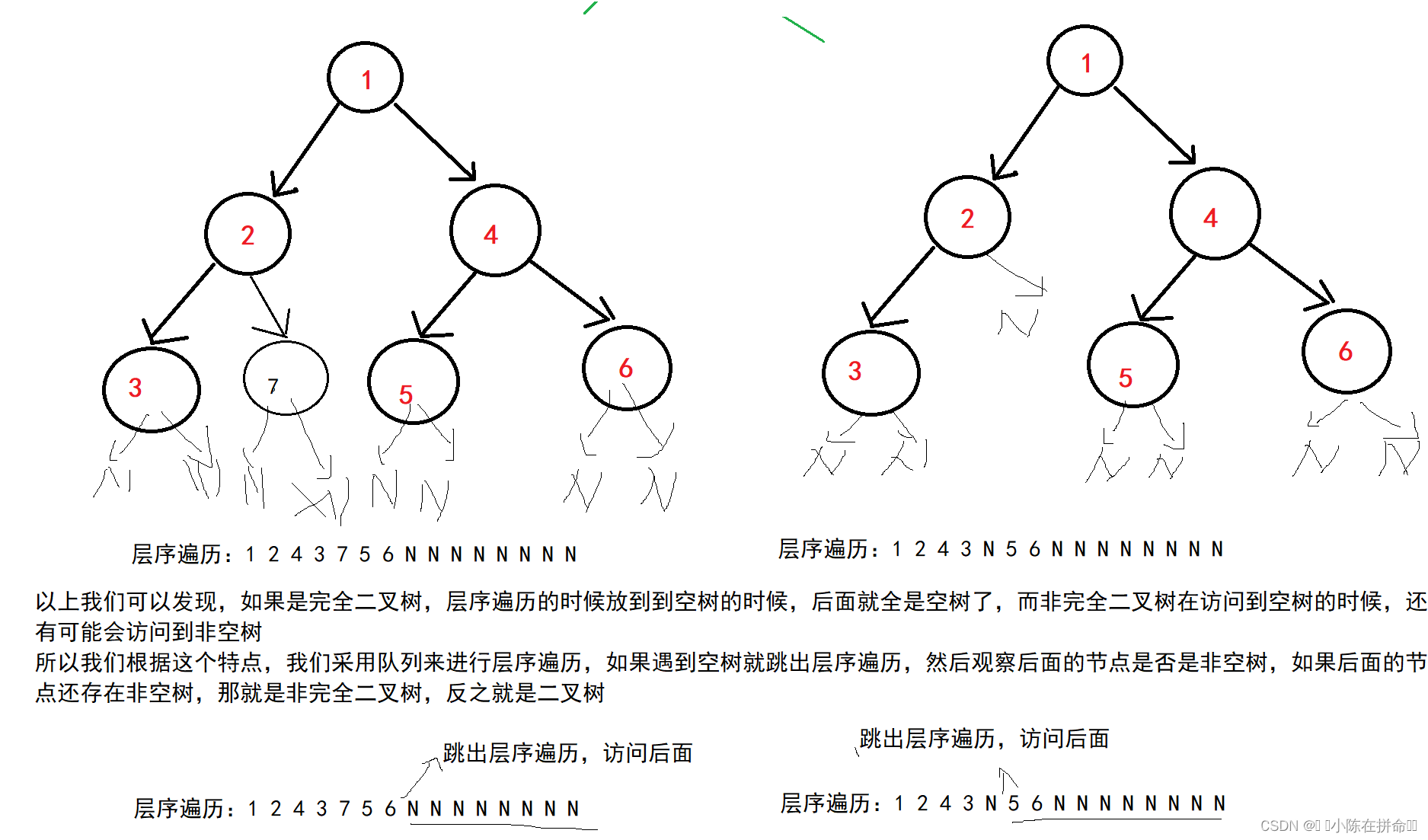
bool BTComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//记录该结果,然后再pop出去QueuePop(&q);if (front == NULL)break;QueuePush(&q, root->left);QueuePush(&q, root->right);}//跳出循环后,检查后面的节点是不是还有非空节点,有的话就是非完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//记录该结果,然后再pop出去QueuePop(&q);if (front){QueueDestory(&q);//队列一定别忘了销毁return false;}QueueDestory(&q);return true;}
}2.15 判断两颗二叉树是否完全相同
我们还是用分治思想,前序遍历比较
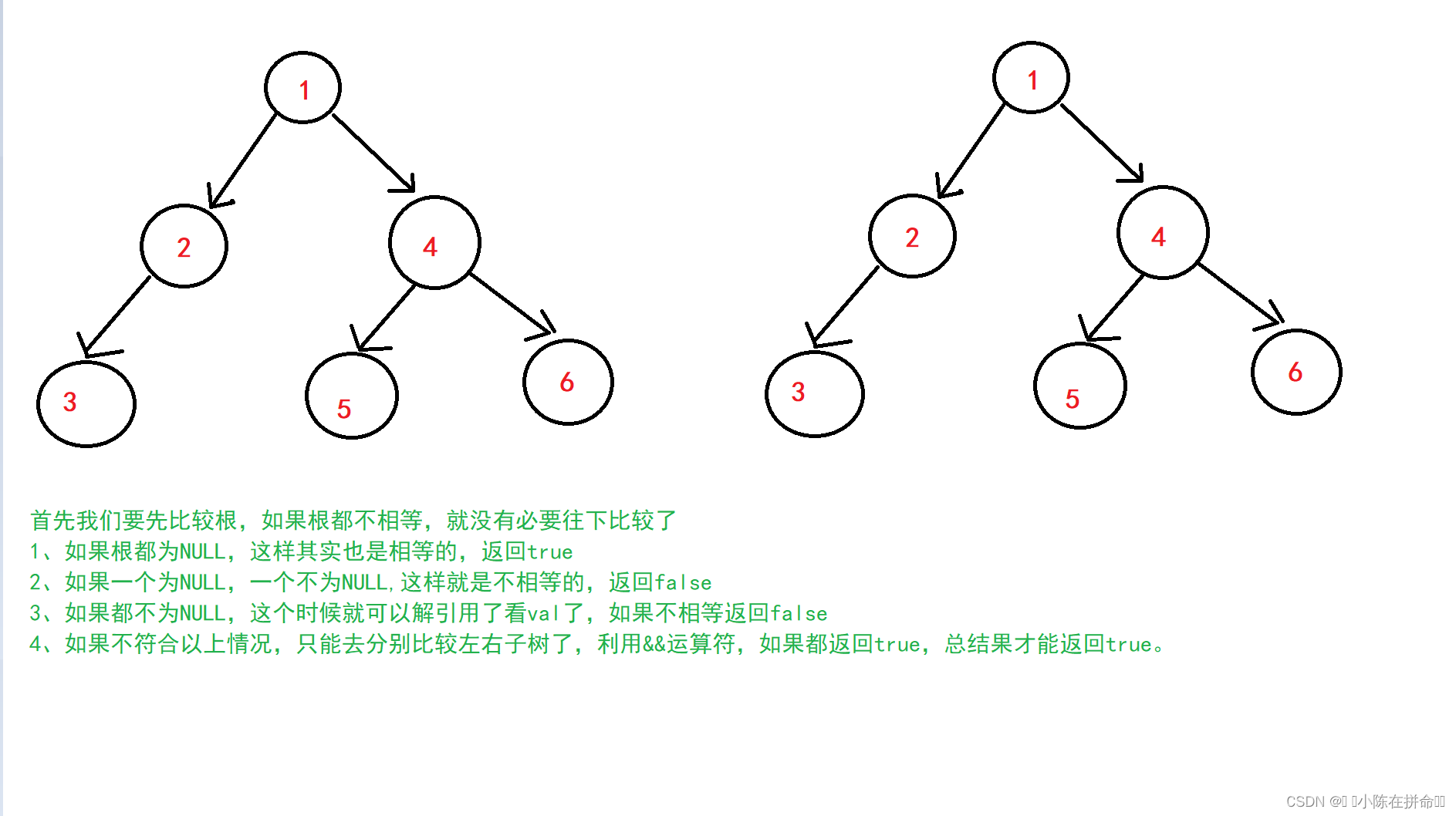
bool IsBTSame(BTNode* root1, BTNode* root2)
{if (root1 == NULL && root2 == NULL)return true;if (root1 == NULL || root2 == NULL)return false;//此时节点肯定不为NULL了,可以解引用找到valif (root1->data != root2->data)return false;//不相等的话只能去找自己的左右子树,左右子树都返回true最后结果才能返回truereturn IsBTSame(root1->left, root2->left) && IsBTSame(root1->right, root2->right);
}三、链式二叉树实现的全部代码
前两个文件只是因为层序遍历和判断完全二叉树会用到,重点还是看后面两个文件
3.1 queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
struct BinaryTreeNode;//为了防止嵌套调用,这里声明一下
typedef struct BinaryTreeNode* QDatatype;//方便后面修改存储数据的数据类型
typedef struct QueueNode//队列结点的数据结构
{QDatatype data;//存储数据struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* phead;//指向队头,用于出队(头删)QNode* ptail;//指向队尾,用于入队(尾插)int size;//记录有效元素个数
}Queue;//创建一个队列相关结构体
void QueueInit(Queue* pq);//队列的初始化
void QueuePush(Queue* pq, QDatatype x);//队列的入队(尾插)
void QueuePop(Queue* pq);//队列的出队(头删)
QDatatype QueueFront(Queue* pq);//获取队列头部元素
QDatatype QueueBack(Queue* pq);//获取队列尾部元素
int QueueSize(Queue* pq);//获取队列中有效元素个数
bool QueueEmpty(Queue* pq);//判断队列是否为空
void QueueDestory(Queue* pq);//队列的销毁
3.2 queue.c
#include"Queue.h"
void QueueInit(Queue* pq)
{assert(pq);//判断传的是不是空指针pq->phead = pq->ptail = NULL;pq->size = 0;//因为队列不像栈一样,有一个top表示栈顶元素的下标//所以如果我们想知道这个队列的有效数据个数,就必须遍历队列//由于其先进先出的特性,我们默认只能访问到头元素和尾元素//所以必须访问一个头元素,就出队列一次,这样才能实现遍历//但是这样的代价太大了,为了方便,我们直接用size
}void QueuePush(Queue* pq, QDatatype x)
{assert(pq);//入队必须从队尾入!QNode* newnode = (QNode*)malloc(sizeof(QNode));//创建一个新节点if (newnode==NULL)//如果新节点申请失败,退出程序{perror("malloc fail");}//新节点创建成功,给新节点初始化一下newnode->data = x;newnode->next = NULL;//开始入队//如果直接尾插的话,由于会用到ptail->next,所以得考虑队列为空的情况if (pq->ptail== NULL)//如果为空,直接把让新节点成为phead和ptail{//按道理来说,如果ptail为空,phead也应该为空// 但是有可能会因为我们的误操作使得phead不为空,这个时候一般是我们写错的问题//所以使用assert来判断一下,有问题的话会及时返回错误信息assert(pq->phead == NULL);pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}void QueuePop(Queue* pq)
{assert(pq);//如果队列为空,没有删除的必要assert(!QueueEmpty(pq));//队列中的出队列相当于链表的头删//如果直接头删,那么如果队列只有一个有效数据的话,那么我们将phead的空间释放掉,但是没有将ptail给置空//这样会导致ptail成为一个野指针,所以我们需要考虑只有一个节点多个节点的情况if (pq->phead->next == NULL)//一个节点的情况,直接将这个节点释放并置空即可{free(pq->phead);pq->phead = pq->ptail = NULL;//置空,防止野指针}else//多个节点的情况,直接头删{QNode* next = pq->phead->next;//临时指针记住下一个节点free(pq->phead);pq->phead = next;//让下一个节点成为新的头}pq->size--;
}QDatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//队列如果为空,则不可能找得到队列头元素//队列不为空的时候,直接返回phead指向的数据return pq->phead->data;
}QDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//队列如果为空,则不可能找得到队尾元素//队列不为空的时候,直接返回ptail指向的数据return pq->ptail->data;
}int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}bool QueueEmpty(Queue* pq)//链表为空的情况,可以根据容量,也可以根据ptail==NULL&&phead==NULL
{assert(pq);return pq->ptail == NULL && pq->phead == NULL;
}void QueueDestory(Queue* pq)
{assert(pq);//判断传的是不是空指针//要逐个节点释放QNode* pcur = pq->phead;while (pcur){QNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
3.3 BT.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include"Queue.h"
typedef int BTDataType;//方便我们后面要存储其他类型的数据的时候方便修改!
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(BTDataType x);
void PreOrder(BTNode* root);//前序遍历
void InOrder(BTNode* root);//中序遍历
void PostOrder(BTNode* root);//后序遍历
void LevelOrder(BTNode* root);//层序遍历
int BTSize(BTNode* root);//二叉树节点个数
int BTLeafSize(BTNode* root);//二叉树的叶子节点个数
int BTLevelKSize(BTNode* root, int k);//二叉树第k层的节点个数
int BTHeight(BTNode* root);//二叉树的高度
BTNode* BTFind(BTNode* root, BTDataType x);//二叉树找值为x的点
BTNode* BTCreate(char* arr,int*pi);//根据前序数组创建二叉树
void BTDestory(BTNode* root);//销毁二叉树
bool BTComplete(BTNode* root);//判断是否完全二叉树
bool IsBTSame(BTNode* root1, BTNode* root2);//判断两个二叉树是否完全相等
3.4 BT.c
#include"BTtree.h"BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL)//如果创建不成功{perror("malloc fail");exit(1);}//如果创建成功newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)//如果不为NULL,就进队列QueuePush(&q, root);while (!QueueEmpty(&q))//队列为空,就是遍历完成{BTNode* front = QueueFront(&q);//让每一次循环过来的节点变成根部,再去访问左右子树QueuePop(&q);//记录完一个元素就出队列printf("%d ", front->data);if(front->left)QueuePush(&q, front->left);//左节点不为空,进队列if (front->right)QueuePush(&q, front->right);//右节点不为空,进队列}printf("\n");//遍历完了就可以销毁队列了QueueDestory(&q);
}int BTSize(BTNode* root)
{return root == NULL ? 0 : BTSize(root->left) + BTSize(root->right) + 1;
}int BTLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BTLeafSize(root->left) + BTLeafSize(root->right);
}int BTLevelKSize(BTNode* root,int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BTLevelKSize(root->left,k-1) + BTLevelKSize(root->right,k-1);
}int BTHeight(BTNode* root)
{if (root == NULL)return 0;int LeftHeight = BTHeight(root->left);int RightHeight = BTHeight(root->right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}BTNode* BTFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* ret1 = BTFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = BTFind(root->right, x);if (ret2)return ret2;return NULL;
}BTNode* BTCreate(char*arr,int*pi)
{if (arr[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BuyNode(arr[*pi]);(*pi)++;root->left = BTCreate(arr, pi);root->right = BTCreate(arr, pi);return root;
}void BTDestory(BTNode* root)
{if (root == NULL)return;BTDestory(root->left);BTDestory(root->right);free(root);//root = NULL;没用
}bool BTComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//记录该结果,然后再pop出去QueuePop(&q);if (front == NULL)break;QueuePush(&q, root->left);QueuePush(&q, root->right);}//跳出循环后,检查后面的节点是不是还有非空节点,有的话就是非完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//记录该结果,然后再pop出去QueuePop(&q);if (front){QueueDestory(&q);//队列一定别忘了销毁return false;}QueueDestory(&q);return true;}
}bool IsBTSame(BTNode* root1, BTNode* root2)
{if (root1 == NULL && root2 == NULL)return true;if (root1 == NULL || root2 == NULL)return false;//此时节点肯定不为NULL了,可以解引用找到valif (root1->data != root2->data)return false;//不相等的话只能去找自己的左右子树,左右子树都返回true最后结果才能返回truereturn IsBTSame(root1->left, root2->left) && IsBTSame(root1->right, root2->right);
}
相关文章:

DS:二叉树的链式结构及实现
创作不易,友友们给个三连吧!! 一、前言 前期我们解释过二叉树的顺序结构(堆)为什么比较适用于完全二叉树,因为如果用数组来实现非完全二叉树,那么数组的中间部分就可能会存在大量的空间浪费。 …...
PhP+vue企业原材料采购系统_cxg0o
伴随着我国社会的发展,人民生活质量日益提高。互联网逐步进入千家万户,改变传统的管理方式,原材料采购系统以互联网为基础,利用php技术,结合vue框架和MySQL数据库开发设计一套原材料采购系统,提高工作效率的…...

C++线程池
原因 如果线程的数量很多,频繁的创建和销毁线程会降低系统的效率。线程池可以使线程复用。 using typedef 内联函数和宏定义区别: 内联函数代替部分#define宏定义;代替普通函数,提高程序效率...
SpringCloud-Hystrix:服务熔断与服务降级
8. Hystrix:服务熔断 分布式系统面临的问题 复杂分布式体系结构中的应用程序有数十个依赖关系,每个依赖关系在某些时候将不可避免失败! 8.1 服务雪崩 多个微服务之间调用的时候,假设微服务A调用微服务B和微服务C,微服…...
浅谈Linux环境
冯诺依曼体系结构: 绝大多数的计算机都遵守冯诺依曼体系结构 在冯诺依曼体系结构下各个硬件相互配合处理数据并反馈结果给用户 其中控制器和运算器统称为中央处理器(CPU),是计算机硬件中最核心的部分,像人类的大脑操控…...
Spring 用法学习总结(一)之基于 XML 注入属性
百度网盘: 👉 Spring学习书籍链接 Spring学习 1 Spring框架概述2 Spring容器3 基于XML方式创建对象4 基于XML方式注入属性4.1 通过set方法注入属性4.2 通过构造器注入属性4.3 使用p命名空间注入属性4.4 注入bean与自动装配4.5 注入集合4.6 注入外部属性…...
免费软件推荐-开源免费批量离线图文识别(OCR)
近期要批量处理图片转电子化,为了解决这个世纪难题,试了很多软件(华为手机自带OCR识别、 PandaOCR、天若OCR、Free OCR)等软件,还是选择了这一款,方便简单 一、什么是OCR? 光学字符识别(Opt…...

2 scala集合-元组和列表
1 元组 元组也是可以存放不同数据类型的元素,并且最重要的是,元组中的元素是不可变的。 例如,定义一个元组,包含字符串 hello,数字 20。如果试图把数字 20 修改为 1,则会报错。 scala> var a ("…...

Spring Boot开启SSL/Https进行交互。
为2个springboot工程开启进行SSL进行交互的认证步骤 //哪个犬玩意举报我侵权的? 一、认证步骤 1、 为服务器生成证书 keytool -genkey -v -alias testServer -keyalg RSA -keystore E:\ssl\testServer.p12 -validity 36500 2、 为客户端生成证书 keytool -genkey -v -alias…...

88.Go设计优雅的错误处理
文章目录 导言一、Go 的约定二、简单错误创建1、 errors.New()2、fmt.Errorf() 三、哨兵错误四、对错误进行编程1、优雅的错误处理设计2、与错误有关的的API 五、总结 导言 在 75.错误码设计、实现统一异常处理和封装统一返回结果 中,我们介绍了错误码的设计&#…...
Python4Delphi: Delphi 程序使用 Python 抓取网页
想用程序去抓取一个网页的内容,Delphi 有自己的 HTTP 库。比如 Indy 的 TIdHTTP,或者 TNetHTTPClient。 这里测试一下使用 Python 的 HTTP 库抓取网页,然后把抓取的内容给 Delphi 的程序。 Delphi 程序,界面上拖控件如下&#x…...

编辑器Zed
什么是Zed 官网:https://zed.dev/ Zed 是 Atom 编辑器原作者主导的新项目 —— 一款支持多人协作的代码编辑器,底层采用 Rust,且默认支持 Rust,还自带了 rust-analyzer,主打 “高性能”,颜值也十分在线&a…...

Java的接口
目录 1.接口的概念 2.语法规则 3.接口的使用 4.接口的特性 总结: 5.实现多个接口 6.接口间的继承 1.接口的概念 接口就是公共的行为规范标准,大家在实现时,只要符合规范标准,就可以通用。 在Java中,接口可以看成…...

【计算机网络】计算机软件工程人工智能研究生复试资料整理
1、JAVA 2、计算机网络 3、计算机体系结构 4、数据库 5、计算机租场原理 6、软件工程 7、大数据 8、英文 自我介绍 2. 计算机网络 1. TCP如何解决丢包和乱序? 序列号:TCP所传送的每段数据都有标有序列号,避免乱序问题发送端确认应答、超时重传:解决丢包问题滑动窗口:避免…...

【Network Management】AUTOSAR架构下CanNm User Data详解
目录 前言 正文 1.CanNm user data概念 2.CanNm user data配置 2.1CDD方式访问CanNm user data...

量子算法入门——2.线性代数与复数
参考资料: 【【零基础入门量子计算-第03讲】线性代数初步与复数】 来自b站up:溴锑锑跃迁 建议关注他的更多高质量文章:CSDN:【溴锑锑跃迁】 0. 前言 强烈建议搭配b站原视频进行观看,这只是我当时看的笔记,…...

分别通过select、多进程、多线程实现一个并发服务器
多进程 #include<myhead.h>#define PORT 8888 //端口号 #define IP "192.168.114.74" //IP地址//定义函数处理客户端信息 int deal_cli_msg(int newfd, struct sockaddr_in cin) {//5、收发数据使用newfd完成通信char buf[128] "&qu…...

如何在 emacs 上开始使用 Tree-Sitter (archlinux)
文章目录 如何在emacs上开始使用Tree-Sitter(archlinux) 如何在emacs上开始使用Tree-Sitter(archlinux) 在archlinux上使用比windows上不知道要方便多少倍! $ sudo pacman -S emacs $ sudo pacman -S tree-sitter这里…...

FL Studio2024最新中文版有哪些其新功能特点?
除了之前提到的特点外,FL Studio 21还有以下一些值得注意的特点: 高效的音频处理:FL Studio 21具备高效的音频处理能力,能够实时处理多轨道音频,提供低延迟的音频播放和录制,确保音乐制作过程中的流畅性和实…...
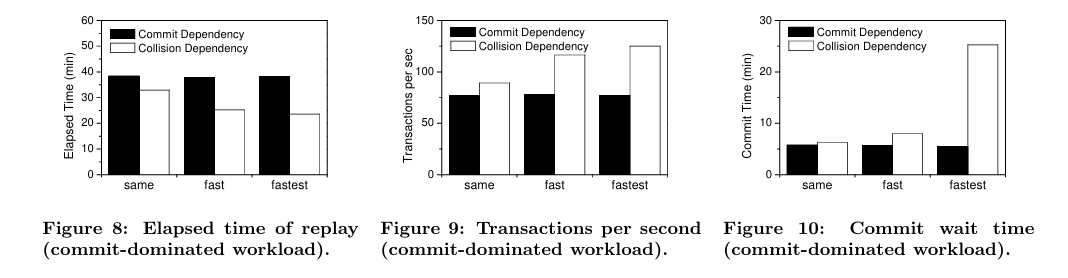
Oracle的学习心得和知识总结(三十二)|Oracle数据库数据库回放功能之论文四翻译及学习
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《Oracle Database SQL Language Reference》 2、参考书籍:《PostgreSQL中文手册》 3、EDB Postgres Advanced Server User Gui…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

