D. Divisible Pairs

思路:我们预处理出每个数分别摸上xy的值,用map存一下,然后遍历每个数,如果a + b是x的倍数的话,那么他们模x的值相加为x,如果a - b是y的倍数的话,那么他们的模y的值相等。
代码:
void solve(){int n, x, y;cin >> n >> x >> y;vector<int>a(n);for(int i = 0;i < n;i ++)cin >> a[i];map<pair<int,int>,int>mp;for(int i = 0;i < n; i++){int lx = a[i] % x;int ly = a[i] % y;mp[{lx,ly}] ++;}int ans = 0;for(int i = 0;i < n; i++){int lx = a[i] % x;int ly = a[i] % y;int cnt = mp[{(x - lx) % x, ly}];if((x - lx) % x == lx){if(cnt)ans += cnt - 1;}else{if(cnt)ans += cnt;}}ans /= 2;cout << ans << endl;
}相关文章:

D. Divisible Pairs
思路:我们预处理出每个数分别摸上xy的值,用map存一下,然后遍历每个数,如果a b是x的倍数的话,那么他们模x的值相加为x,如果a - b是y的倍数的话,那么他们的模y的值相等。 代码: voi…...

【教程】Kotlin语言学习笔记(二)——数据类型(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【Kotlin语言学习】系列文章 第一章 《认识Kotlin》 第二章 《数据类型》 文章目录 【Kotlin语言学习】系列文章一、基本数据…...

react 插槽
问题开发当中会经常出现组件十分相似的组件,只有一部分是不同的 解决: 父组件:在引用的时候 import { Component } from "react"; import Me from "../me";const name <div>名称</div> class Shoop extends Compone…...

Linux运用fork函数创建进程
fork函数: 函数原型: pid_t fork(void); 父进程调用fork函数创建一个子进程,子进程的用户区父进程的用户区完全一样,但是内核区不完全一样;如父进程的PID和子进程的PID不一样。 返回值: RETURN VALUEO…...

Pytest测试技巧之Fixture:模块化管理测试数据
在 Pytest 测试中,有效管理测试数据是提高测试质量和可维护性的关键。本文将深入探讨 Pytest 中的 Fixture,特别是如何利用 Fixture 实现测试数据的模块化管理,以提高测试用例的清晰度和可复用性。 什么是Fixture? 在 Pytest 中&a…...

设计模式-职责链模式Chain of Responsibility
职责链模式 一、原理和实现二、实现方式1) 使用链表实现2) 使用数组实现3) 扩展 作用:复用和扩展,在实际的项目开发中比较常用。在框架开发中,我们也可以利用它们来提供框架的扩展点,能够让框架的使用者在不修改框架源码的情况下&…...

书生浦语大模型实战营-课程作业(3)
下载sentence_transformer的代码运行情况。sentence_transformer用于embedding(转向量) 本地构建持久化向量数据库。就是把txt和md文件抽取出纯文本,分割成定长(500)后转换成向量,保存到本地,称…...

考研英语单词25
Day 25 bench n.长凳 elastic n.橡皮圈,松紧带 a.灵活的 “e-last 延伸出去” disaster n.灾难,灾祸【disastrous a.灾难性的,极坏的】 deadly a.致命的,极端的,势不两立的 hike n.徒步旅行&…...

计算机网络——08应用层原理
应用层原理 创建一个新的网络 编程 在不同的端系统上运行通过网络基础设施提供的服务,应用进程批次通信如Web Web服务器软件与浏览器软件通信 网络核心中没有应用层软件 网络核心没有应用层功能网络应用只能在端系统上存在 快速网络应用开发和部署 网络应用…...

面试计算机网络框架八股文十问十答第五期
面试计算机网络框架八股文十问十答第五期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)与缓存相关的HTTP请…...
拟合案例1:matlab积分函数拟合详细步骤及源码
本文介绍一下基于matlab实现积分函数拟合的过程。采用的工具是lsqcurvefit和nlinfit两个函数工具。关于包含积分运算的函数,这里可以分为两大类啊。我们用具体的案例来展示:一种是积分运算中不包含这个自变量,如下图的第一个公式,也就是说它这个积分运算只有R和Q这两个待定…...

嵌入式软件设计入门:从零开始学习嵌入式软件设计
(本文为简单介绍,个人观点仅供参考) 首先,让我们了解一下嵌入式软件的定义。嵌入式软件是指运行在嵌入式系统中的特定用途软件,它通常被用来控制硬件设备、处理实时数据和实现特定功能。与桌面应用程序相比,嵌入式软件需要具备更高的实时性、…...

Educational Codeforces Round 135 (Rated for Div. 2)C. Digital Logarithm(思维)
文章目录 题目链接题意题解代码 题目链接 C. Digital Logarithm 题意 给两个长度位 n n n的数组 a a a、 b b b,一个操作 f f f 定义操作 f f f为, a [ i ] f ( a [ i ] ) a [ i ] a[i]f(a[i])a[i] a[i]f(a[i])a[i]的位数 求最少多少次操作可以使 …...
微信小程序介绍、账号申请、开发者工具目录结构详解及小程序配置
目录 一、微信小程序介绍 1.什么是小程序? 2.小程序可以干什么? 3.微信小程序特点 二、账号申请 1.账号注册 2.测试号申请 三、安装开发工具 四、开发小程序 五、目录结构 JSON 配置 小程序配置 app.json 工具配置 project.config.json 页…...

数字的魅力之情有独钟的素数
情有独钟的素数 什么是素数 素数(Prime number)也称为质数,是指在非0自然数中,除了1与其本身之外不拥有其他因数的自然数。也就是说,素数需要满足两个条件: 大于1的整数;只拥有1和其自身两个…...

Vue2源码梳理:render函数的实现
render 在 $mount 时,会调用 render 方法在写 template 时,最终也会转换成 render 方法Vue 的 _render 方法是实例的一个私有方法,它用来把实例渲染成一个虚拟 Node它的定义在 src/core/instance/render.js 文件中,它返回的是一个…...
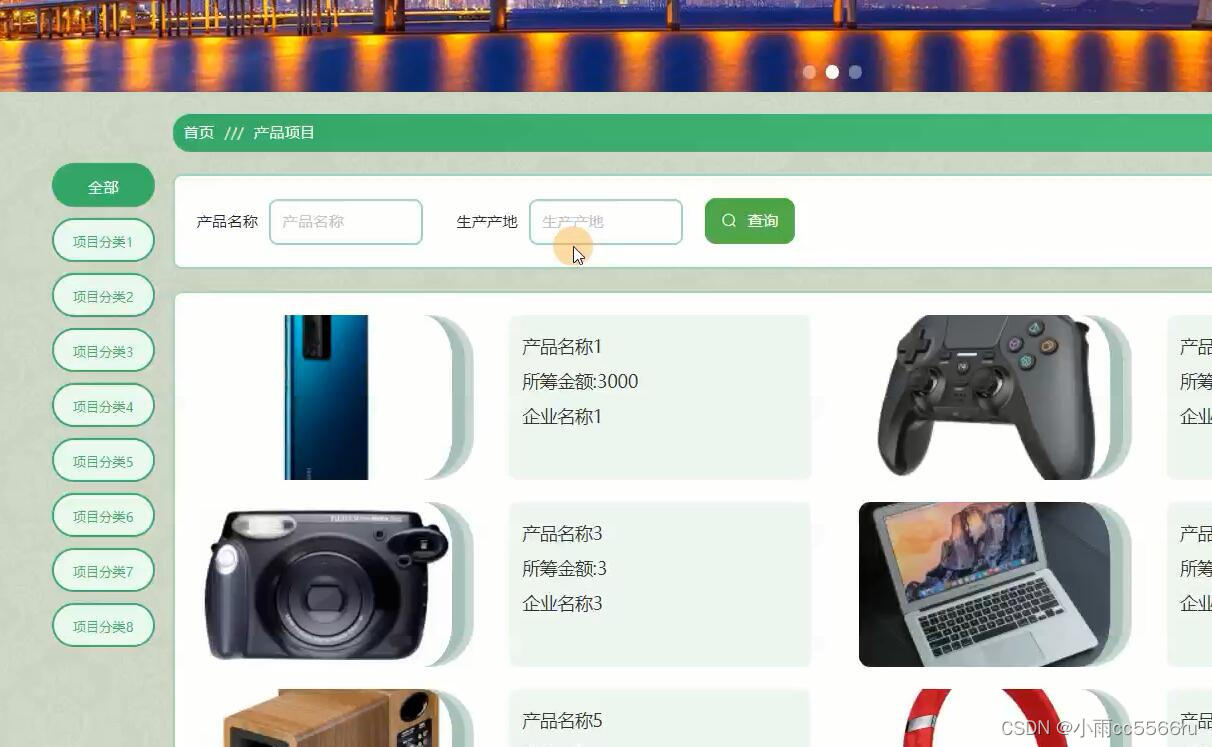
flask+python企业产品订单管理系统938re
在设计中采用“自下而上”的思想,在创新型产品提前购模块实现了个人中心、个体管理、发布企业管理、投资企业管理、项目分类管理、产品项目管理、个体投资管理、企业投资管理、个体订单管理、企业订单管理、系统管理等的功能性进行操作。最终,对基本系统…...

Vue2源码梳理:关于数据驱动,与new Vue时的初始化操作
数据驱动 1 )概述 vue的一个核心思想,就是数据驱动 所谓数据驱动,就是指视图是由数据驱动生成的 对视图的修改并不会直接操作dom,而是通过修改数据 它相比我们传统的前端开发,如使用 jQuery 的前端库直接去修改 dom…...
【C++航海王:追寻罗杰的编程之路】关于模板,你知道哪些?
目录 1 -> 泛型编程 2 -> 函数模板 2.1 -> 函数模板概念 2.2 -> 函数模板格式 2.3 -> 函数模板的原理 2.4 -> 函数模板的实例化 2.5 -> 函数参数的匹配原则 3 -> 类模板 3.1 -> 类模板的定义格式 3.2 -> 类模板的实例化 1 -> 泛型编…...
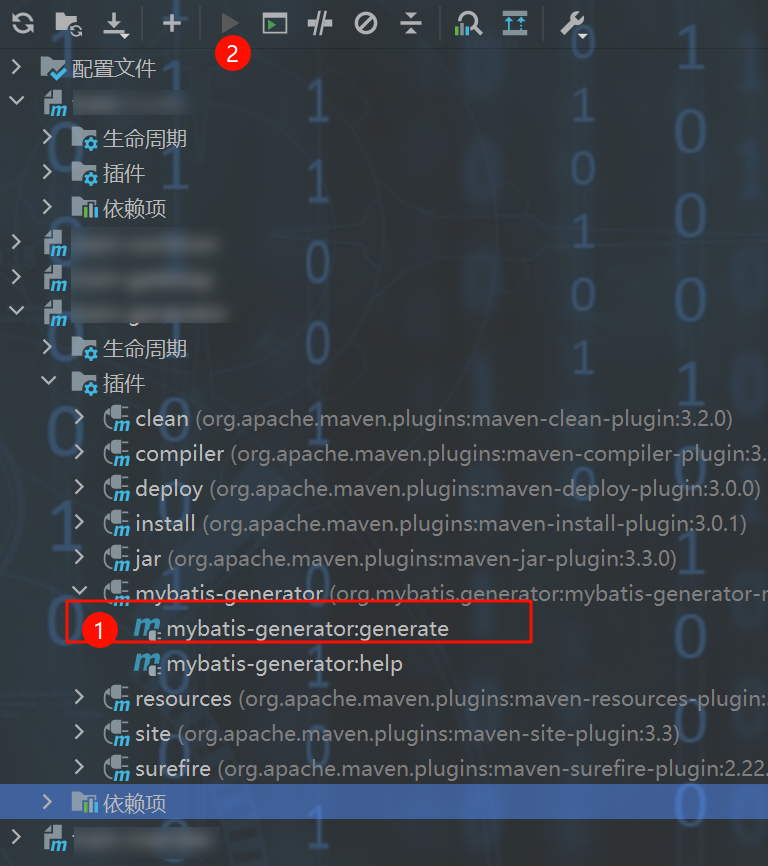
分布式springboot 3项目集成mybatis官方生成器开发记录
文章目录 说明实现思路实现步骤第一步:创建generator子模块第二步:引入相关maven插件和依赖第三步:编写生成器配置文件第四步:运行查看结果 说明 该文章为作者开发学习记录,方便以后复习和交流主要内容为:…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
