二维差分---三维差分算法笔记

文章目录
- 一.二维差分
- 构造差分二维数组
- 二维差分算法
- 状态dp求b[i][j]数组的二维前缀和图解
- 二.三维前缀和与差分
- 三维前缀和图解:
- 三维差分核心公式图解:
- 模板题
一.二维差分
- 给定一个原二维数组
a[i][j],若要给a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数c,暴力的做法时间复杂度为O(N^2),使用二维差分可以在O(1)的时间复杂度内完成该操作
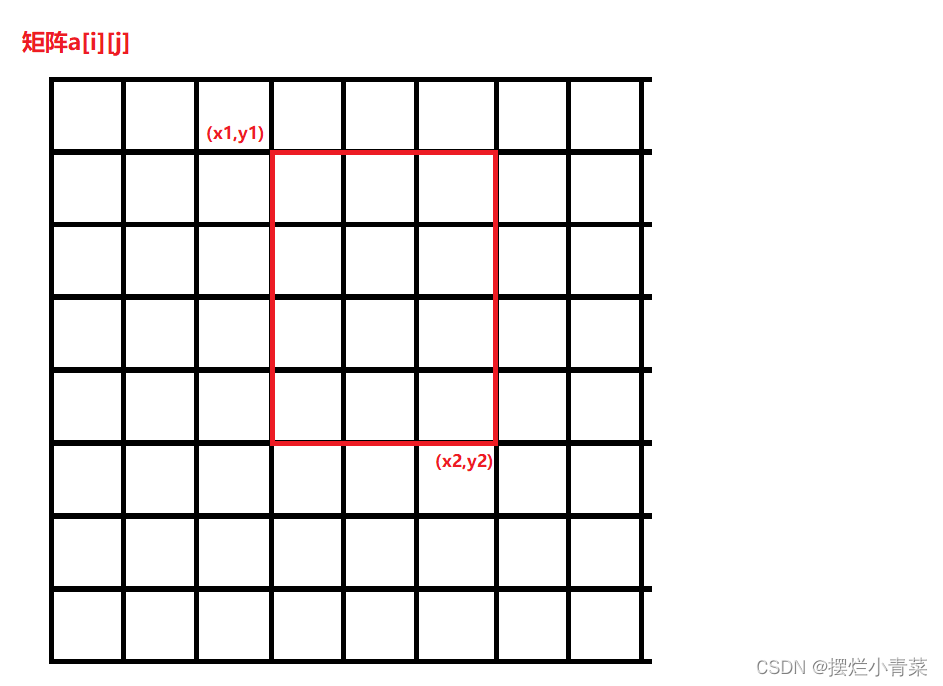
构造差分二维数组
- 构造差分二维数组
b[i][j]使得原二维数组a[i][j]是二维数组b[i][j]的二维前缀和数组,即满足:
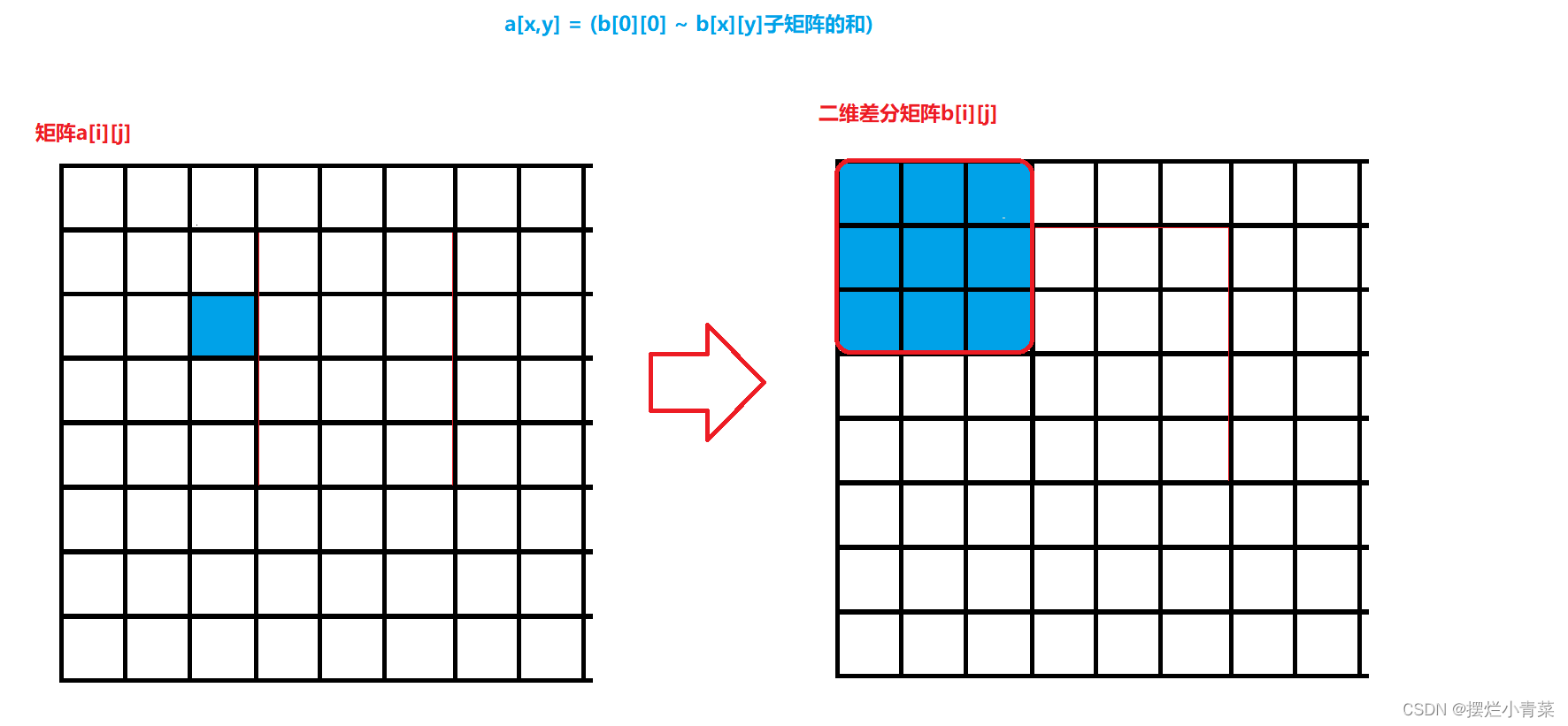
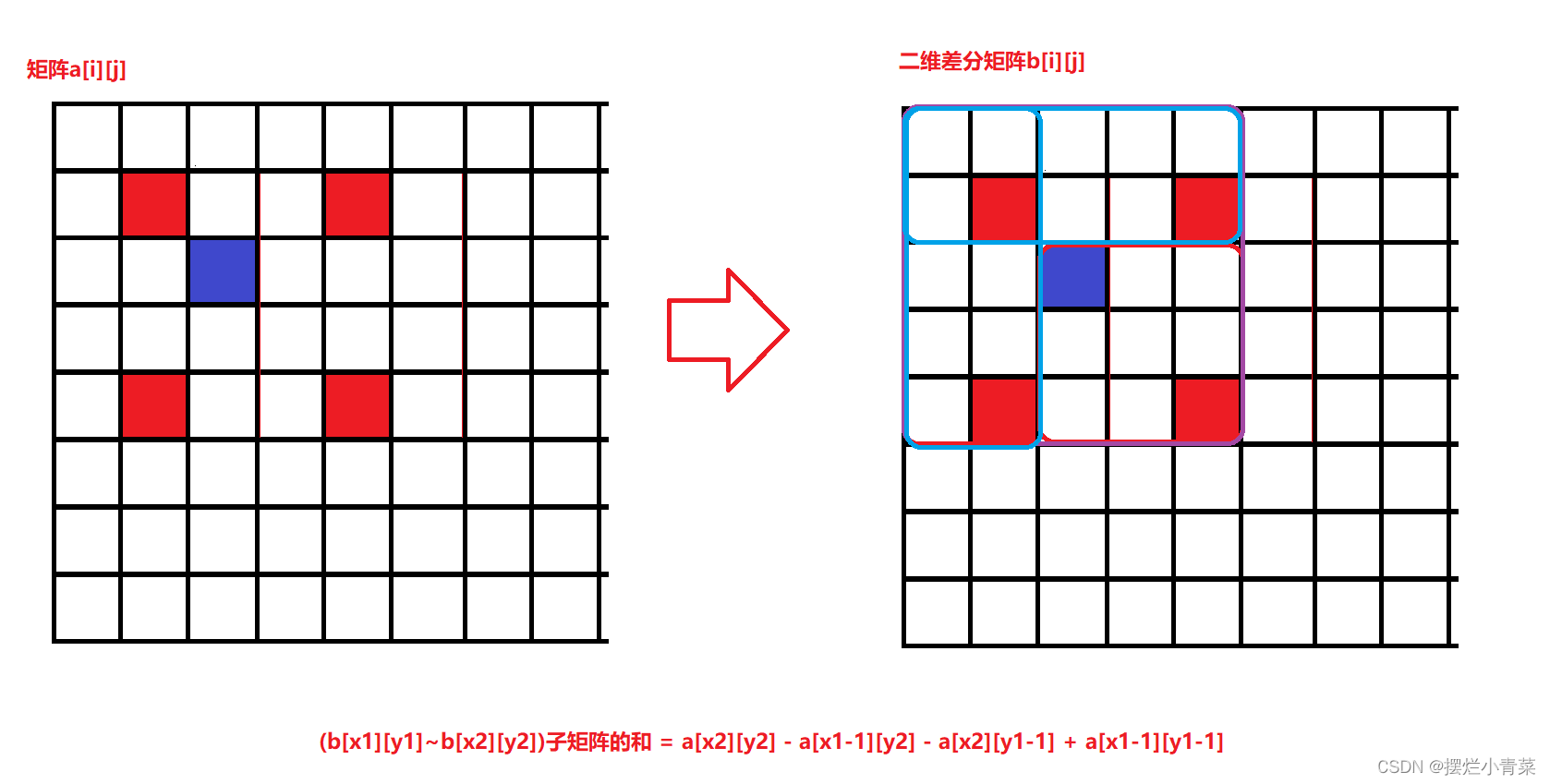
二维差分算法
- 若使原数组
a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数c,等价于对b[i][j]数组进行如下操作:b[x1][y1] += cb[x2+1][y2+1] += cb[x2+1][y1] -= cb[x1][y2+1] -= c
- 核心操作接口:
//使原数组a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数c
//接口可以用于构造差分矩阵以及进行原数组的矩阵元素整体修改操作
void Matrix_Add(long long(*b)[1010],int x1 ,int y1,int x2 ,int y2,int c){b[x1][y1] += c;b[x2+1][y2+1] += c;b[x1][y2+1] -= c;b[x2+1][y1] -= c;
}
//状态递推法对b[i][j]数组求二维前缀和,以获取原数组的元素--> 默认矩阵第0行第0列全部元素为0
void Get_Pre_Sum(long long(*b)[1010],int row , int col){//求(1,1)~(i,j)的子矩阵的和for(int i = 1 ; i <= row ; ++i){for(int j = 1 ; j<=col ; ++j){b[i][j] += (b[i-1][j] + b[i][j-1] - b[i-1][j-1]);}}
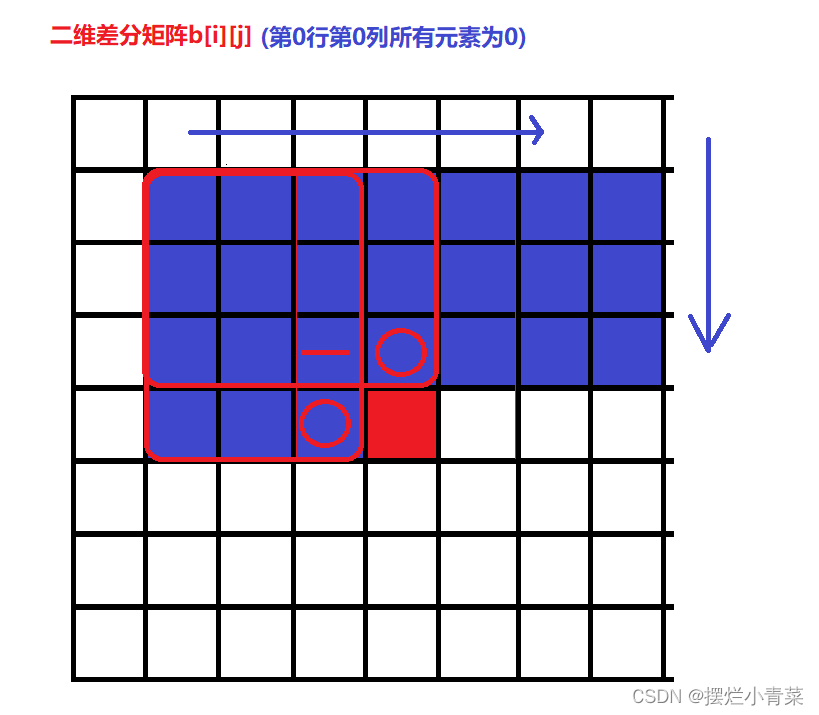
}- 求出
b[i][j]数组的二维前缀和就可以恢复原数组a[i][j]
状态dp求b[i][j]数组的二维前缀和图解
二.三维前缀和与差分
三维前缀和图解:
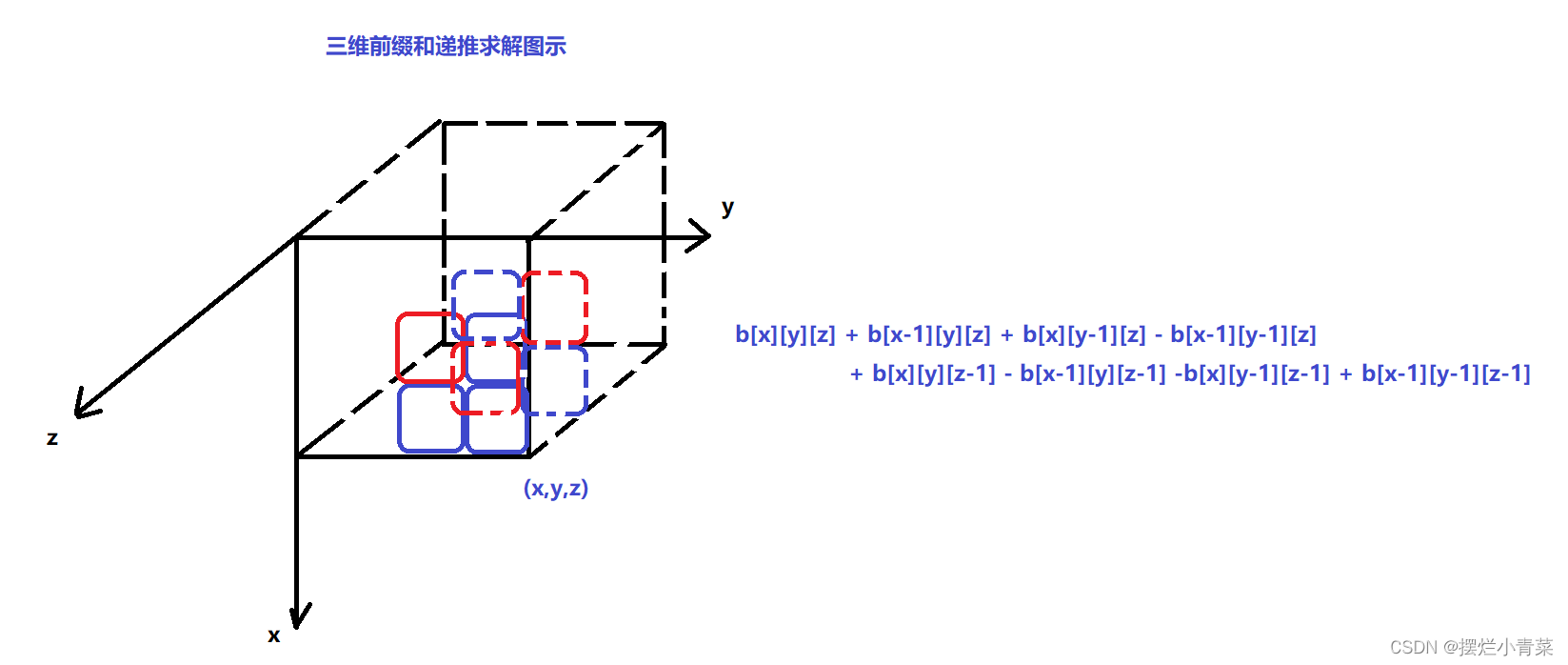
- 前缀和递推构造接口:
void Get_Pre_Sum(vector<vector<vector<long long>>>& Board,int high,int row,int col ){for(int i = 1 ; i <= high ; ++i){for(int j = 1 ; j <= row ; ++j){for(int k = 1 ; k <= col ; ++k){Board[i][j][k] += Board[i-1][j][k] + Board[i][j-1][k] - Board[i-1][j-1][k] +Board[i][j][k-1] - Board[i-1][j][k-1] - Board[i][j-1][k-1] + Board[i-1][j-1][k-1];}}}
}
三维差分核心公式图解:
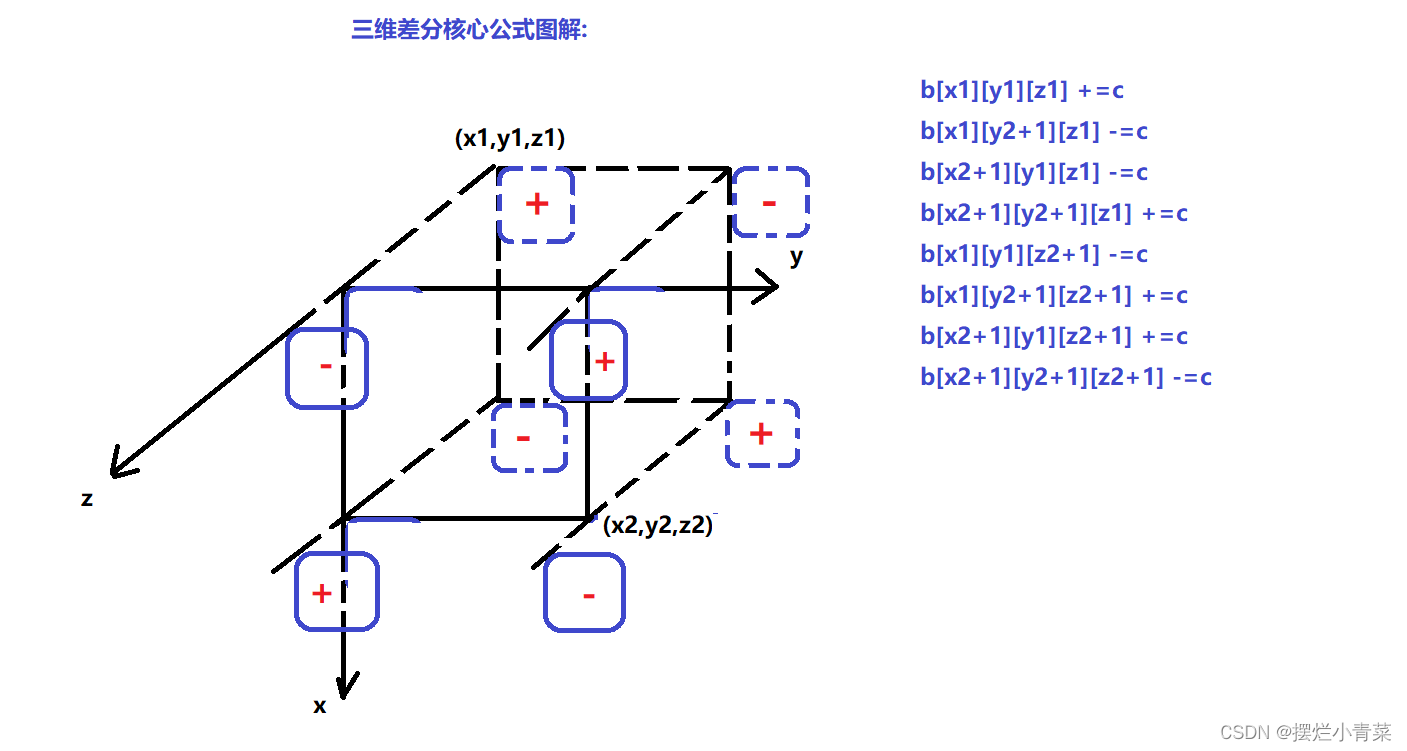
- "相邻点"的加减满足容斥关系,
相邻互斥,相间相容 - 核心公式接口:
void Matrix_Add(vector<vector<vector<long long>>>& Board,int x1 , int y1 , int z1 , int x2 , int y2 , int z2 , int c){Board[x1][y1][z1] += c;Board[x1][y2+1][z1] -= c;Board[x2+1][y1][z1] -= c;Board[x2+1][y2+1][z1] += c;Board[x1][y1][z2+1] -= c;Board[x1][y2+1][z2+1] += c;Board[x2+1][y1][z2+1] += c;Board[x2+1][y2+1][z2+1] -= c;
}模板题
差分模板题1
差分模板题2

相关文章:

二维差分---三维差分算法笔记
文章目录 一.二维差分构造差分二维数组二维差分算法状态dp求b[i][j]数组的二维前缀和图解 二.三维前缀和与差分三维前缀和图解:三维差分核心公式图解:模板题 一.二维差分 给定一个原二维数组a[i][j],若要给a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数…...

D. Divisible Pairs
思路:我们预处理出每个数分别摸上xy的值,用map存一下,然后遍历每个数,如果a b是x的倍数的话,那么他们模x的值相加为x,如果a - b是y的倍数的话,那么他们的模y的值相等。 代码: voi…...

【教程】Kotlin语言学习笔记(二)——数据类型(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【Kotlin语言学习】系列文章 第一章 《认识Kotlin》 第二章 《数据类型》 文章目录 【Kotlin语言学习】系列文章一、基本数据…...

react 插槽
问题开发当中会经常出现组件十分相似的组件,只有一部分是不同的 解决: 父组件:在引用的时候 import { Component } from "react"; import Me from "../me";const name <div>名称</div> class Shoop extends Compone…...

Linux运用fork函数创建进程
fork函数: 函数原型: pid_t fork(void); 父进程调用fork函数创建一个子进程,子进程的用户区父进程的用户区完全一样,但是内核区不完全一样;如父进程的PID和子进程的PID不一样。 返回值: RETURN VALUEO…...

Pytest测试技巧之Fixture:模块化管理测试数据
在 Pytest 测试中,有效管理测试数据是提高测试质量和可维护性的关键。本文将深入探讨 Pytest 中的 Fixture,特别是如何利用 Fixture 实现测试数据的模块化管理,以提高测试用例的清晰度和可复用性。 什么是Fixture? 在 Pytest 中&a…...

设计模式-职责链模式Chain of Responsibility
职责链模式 一、原理和实现二、实现方式1) 使用链表实现2) 使用数组实现3) 扩展 作用:复用和扩展,在实际的项目开发中比较常用。在框架开发中,我们也可以利用它们来提供框架的扩展点,能够让框架的使用者在不修改框架源码的情况下&…...

书生浦语大模型实战营-课程作业(3)
下载sentence_transformer的代码运行情况。sentence_transformer用于embedding(转向量) 本地构建持久化向量数据库。就是把txt和md文件抽取出纯文本,分割成定长(500)后转换成向量,保存到本地,称…...

考研英语单词25
Day 25 bench n.长凳 elastic n.橡皮圈,松紧带 a.灵活的 “e-last 延伸出去” disaster n.灾难,灾祸【disastrous a.灾难性的,极坏的】 deadly a.致命的,极端的,势不两立的 hike n.徒步旅行&…...

计算机网络——08应用层原理
应用层原理 创建一个新的网络 编程 在不同的端系统上运行通过网络基础设施提供的服务,应用进程批次通信如Web Web服务器软件与浏览器软件通信 网络核心中没有应用层软件 网络核心没有应用层功能网络应用只能在端系统上存在 快速网络应用开发和部署 网络应用…...

面试计算机网络框架八股文十问十答第五期
面试计算机网络框架八股文十问十答第五期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)与缓存相关的HTTP请…...
拟合案例1:matlab积分函数拟合详细步骤及源码
本文介绍一下基于matlab实现积分函数拟合的过程。采用的工具是lsqcurvefit和nlinfit两个函数工具。关于包含积分运算的函数,这里可以分为两大类啊。我们用具体的案例来展示:一种是积分运算中不包含这个自变量,如下图的第一个公式,也就是说它这个积分运算只有R和Q这两个待定…...

嵌入式软件设计入门:从零开始学习嵌入式软件设计
(本文为简单介绍,个人观点仅供参考) 首先,让我们了解一下嵌入式软件的定义。嵌入式软件是指运行在嵌入式系统中的特定用途软件,它通常被用来控制硬件设备、处理实时数据和实现特定功能。与桌面应用程序相比,嵌入式软件需要具备更高的实时性、…...

Educational Codeforces Round 135 (Rated for Div. 2)C. Digital Logarithm(思维)
文章目录 题目链接题意题解代码 题目链接 C. Digital Logarithm 题意 给两个长度位 n n n的数组 a a a、 b b b,一个操作 f f f 定义操作 f f f为, a [ i ] f ( a [ i ] ) a [ i ] a[i]f(a[i])a[i] a[i]f(a[i])a[i]的位数 求最少多少次操作可以使 …...
微信小程序介绍、账号申请、开发者工具目录结构详解及小程序配置
目录 一、微信小程序介绍 1.什么是小程序? 2.小程序可以干什么? 3.微信小程序特点 二、账号申请 1.账号注册 2.测试号申请 三、安装开发工具 四、开发小程序 五、目录结构 JSON 配置 小程序配置 app.json 工具配置 project.config.json 页…...

数字的魅力之情有独钟的素数
情有独钟的素数 什么是素数 素数(Prime number)也称为质数,是指在非0自然数中,除了1与其本身之外不拥有其他因数的自然数。也就是说,素数需要满足两个条件: 大于1的整数;只拥有1和其自身两个…...

Vue2源码梳理:render函数的实现
render 在 $mount 时,会调用 render 方法在写 template 时,最终也会转换成 render 方法Vue 的 _render 方法是实例的一个私有方法,它用来把实例渲染成一个虚拟 Node它的定义在 src/core/instance/render.js 文件中,它返回的是一个…...
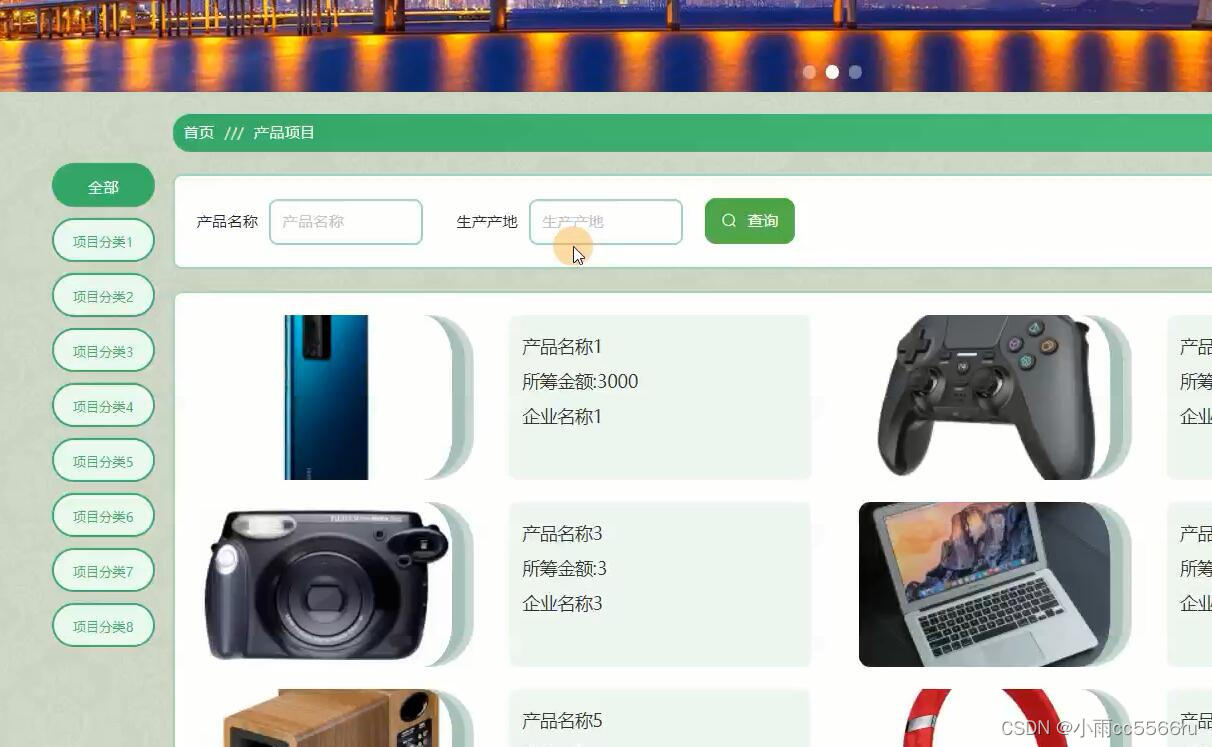
flask+python企业产品订单管理系统938re
在设计中采用“自下而上”的思想,在创新型产品提前购模块实现了个人中心、个体管理、发布企业管理、投资企业管理、项目分类管理、产品项目管理、个体投资管理、企业投资管理、个体订单管理、企业订单管理、系统管理等的功能性进行操作。最终,对基本系统…...

Vue2源码梳理:关于数据驱动,与new Vue时的初始化操作
数据驱动 1 )概述 vue的一个核心思想,就是数据驱动 所谓数据驱动,就是指视图是由数据驱动生成的 对视图的修改并不会直接操作dom,而是通过修改数据 它相比我们传统的前端开发,如使用 jQuery 的前端库直接去修改 dom…...
【C++航海王:追寻罗杰的编程之路】关于模板,你知道哪些?
目录 1 -> 泛型编程 2 -> 函数模板 2.1 -> 函数模板概念 2.2 -> 函数模板格式 2.3 -> 函数模板的原理 2.4 -> 函数模板的实例化 2.5 -> 函数参数的匹配原则 3 -> 类模板 3.1 -> 类模板的定义格式 3.2 -> 类模板的实例化 1 -> 泛型编…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
