XGB-5: DART Booster
XGBoost 主要结合了大量的回归树和一个小的学习率。在这种情况下,早期添加的树是重要的,而晚期添加的树是不重要的。
Vinayak 和 Gilad-Bachrach 提出了一种将深度神经网络社区的 dropout 技术应用于梯度提升树的新方法,并在某些情况下报告了更好的结果。
以下是新的树增强器 dart 的说明。
原始论文
Rashmi Korlakai Vinayak, Ran Gilad-Bachrach。“DART: Dropouts meet Multiple Additive Regression Trees.” [arXiv]。
特性
- 通过删除树来解决过拟合问题。
- 可以阻止不重要的普通树(以纠正普通错误)
由于训练中引入的随机性,可以期待以下一些差异:
-
由于随机丢弃dropout会阻止使用预测缓冲区,因此训练可能比
gbtree慢 -
由于随机性,早停Early-stop可能不稳定
工作原理
-
在第 m m m训练轮次中,假设 k k k棵树被选中丢弃。
-
令 D = ∑ i ∈ K F i D = \sum_{i \in \mathbf{K}} F_i D=∑i∈KFi为被丢弃树的叶节点分数, F m = η F ~ m F_m = \eta \tilde{F}_m Fm=ηF~m为新树的叶节点分数。
-
目标函数如下:
O b j = ∑ j = 1 n L ( y j , y ^ j m − 1 − D j + F ~ m ) Ω ( F ~ m ) . \mathrm{Obj} = \sum_{j=1}^n L \left( y_j, \hat{y}_j^{m-1} - D_j + \tilde{F}_m \right)\Omega \left( \tilde{F}_m \right). Obj=j=1∑nL(yj,y^jm−1−Dj+F~m)Ω(F~m).
- D D D和 F m F_m Fm是超调,因此使用缩放因子
y ^ j m = ∑ i ∉ K F i + a ( ∑ i ∈ K F i + b F m ) . \hat{y}_j^m = \sum_{i \not\in \mathbf{K}} F_i + a \left( \sum_{i \in \mathbf{K}} F_i + b F_m \right) . y^jm=i∈K∑Fi+a(i∈K∑Fi+bFm).
参数
Booster dart 继承自 gbtree booster,因此支持 gbtree 的所有参数,比如 eta、gamma、max_depth 等。
以下是额外的参数:
-
sample_type:采样算法的类型。uniform:(默认)以均匀方式选择要删除的树。weighted:以权重比例选择要删除的树。
-
normalize_type:规范化算法的类型。-
tree:(默认)新树的权重与每个被删除的树相同。
a ( ∑ i ∈ K F i + 1 k F m ) = a ( ∑ i ∈ K F i + η k F ~ m ) ∼ a ( 1 + η k ) D = a k + η k D = D , a = k k + η \begin{split}a \left( \sum_{i \in \mathbf{K}} F_i + \frac{1}{k} F_m \right) &= a \left( \sum_{i \in \mathbf{K}} F_i + \frac{\eta}{k} \tilde{F}_m \right) \\ &\sim a \left( 1 + \frac{\eta}{k} \right) D \\ &= a \frac{k + \eta}{k} D = D , \\ &\quad a = \frac{k}{k + \eta}\end{split} a(i∈K∑Fi+k1Fm)=a(i∈K∑Fi+kηF~m)∼a(1+kη)D=akk+ηD=D,a=k+ηk
-
forest:新树的权重等于被删除的树的权重之和(森林)。
a ( ∑ i ∈ K F i + F m ) = a ( ∑ i ∈ K F i + η F ~ m ) ∼ a ( 1 + η ) D = a ( 1 + η ) D = D , a = 1 1 + η . \begin{split}a \left( \sum_{i \in \mathbf{K}} F_i + F_m \right) &= a \left( \sum_{i \in \mathbf{K}} F_i + \eta \tilde{F}_m \right) \\ &\sim a \left( 1 + \eta \right) D \\ &= a (1 + \eta) D = D , \\ &\quad a = \frac{1}{1 + \eta} .\end{split} a(i∈K∑Fi+Fm)=a(i∈K∑Fi+ηF~m)∼a(1+η)D=a(1+η)D=D,a=1+η1.
-
-
dropout_rate: 丢弃率。
- 范围:[0.0, 1.0]
-
skip_dropout: 跳过丢弃的概率。
- 如果跳过了dropout,新树将以与 gbtree 相同的方式添加。
- 范围:[0.0, 1.0]
示例
import xgboost as xgb# read in data
dtrain = xgb.DMatrix('./xgboost/demo/data/agaricus.txt.train?format=libsvm')
dtest = xgb.DMatrix('./xgboost/demo/data/agaricus.txt.test?format=libsvm')# specify parameters via map
param = {'booster': 'dart','max_depth': 5, 'learning_rate': 0.1,'objective': 'binary:logistic','sample_type': 'uniform','normalize_type': 'tree','rate_drop': 0.1,'skip_drop': 0.5}num_round = 50
bst = xgb.train(param, dtrain, num_round)
preds = bst.predict(dtest)
参考
- https://xgboost.readthedocs.io/en/latest/tutorials/dart.html
- https://arxiv.org/abs/1505.01866
相关文章:

XGB-5: DART Booster
XGBoost 主要结合了大量的回归树和一个小的学习率。在这种情况下,早期添加的树是重要的,而晚期添加的树是不重要的。 Vinayak 和 Gilad-Bachrach 提出了一种将深度神经网络社区的 dropout 技术应用于梯度提升树的新方法,并在某些情况下报告了…...
HiveSQL——不使用union all的情况下进行列转行
参考文章: HiveSql一天一个小技巧:如何不使用union all 进行列转行_不 union all-CSDN博客文章浏览阅读881次,点赞5次,收藏10次。本文给出一种不使用传统UNION ALL方法进行 行转列的方法,其中方法一采用了concat_wsposexplode()方…...
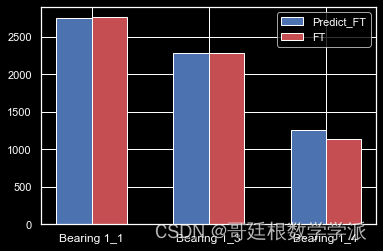
Python环境下基于指数退化模型和LSTM自编码器的轴承剩余寿命预测
滚动轴承是机械设备中关键的零部件之一,其可靠性直接影响了设备的性能,所以对滚动轴承的剩余使用寿命(RUL)进行预测是十分必要的。目前,如何准确地对滚动轴承剩余使用寿命进行预测,仍是一个具有挑战的课题。对滚动轴承剩余寿命评估…...
)
无人机竞赛视觉算法开发流程开源计划(询问大家意见)
本科中参加过一系列的无人机机器人竞赛,像电赛、工训赛、机器人大赛这些,有一些比较常用的方案打算开源一下。现在读研了,也算是对本科的一个总结,但是还是想看看大家意见,大家有什么需求可以在评论区说,我…...
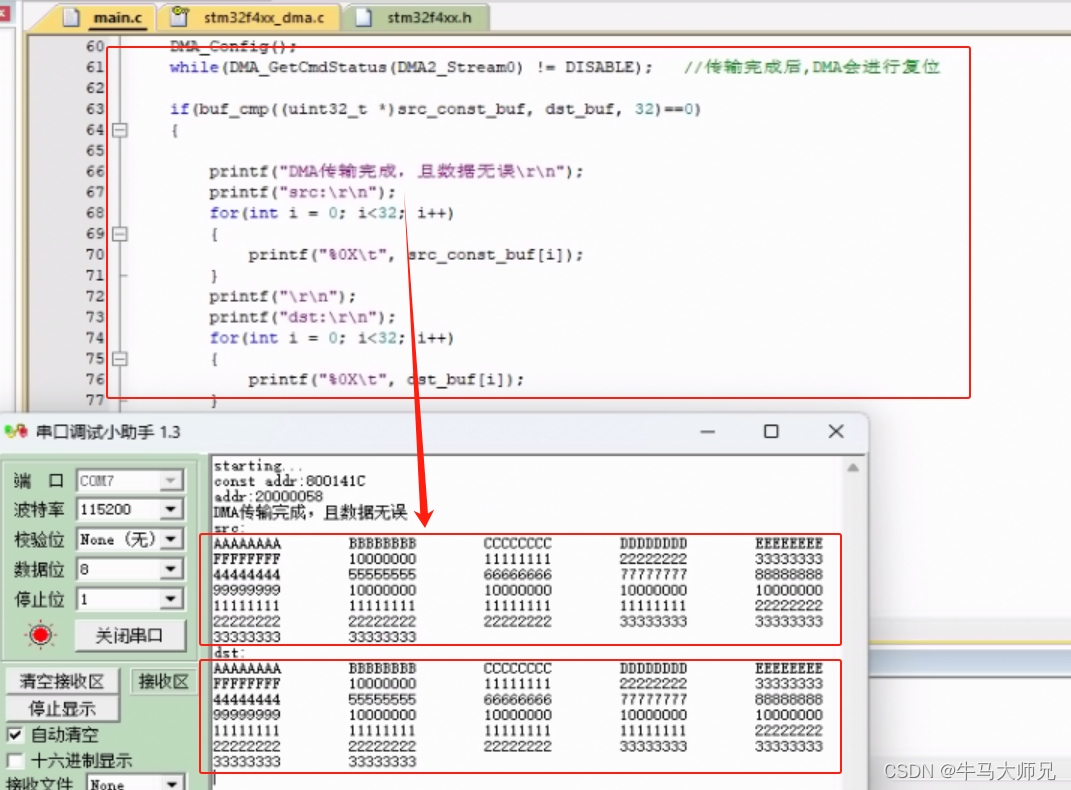
DMA直接内存访问,STM32实现高速数据传输使用配置
1、DMA运用场景 随着智能化、信息化的不断推进,嵌入式设备的数据处理量也呈现指数级增加,因此对于巨大的数据量处理的情况时,必须采取其它的方式去替CPU减负,以保证嵌入式设备性能。例如SD卡存储器和音视频、网络高速通信等其它情…...
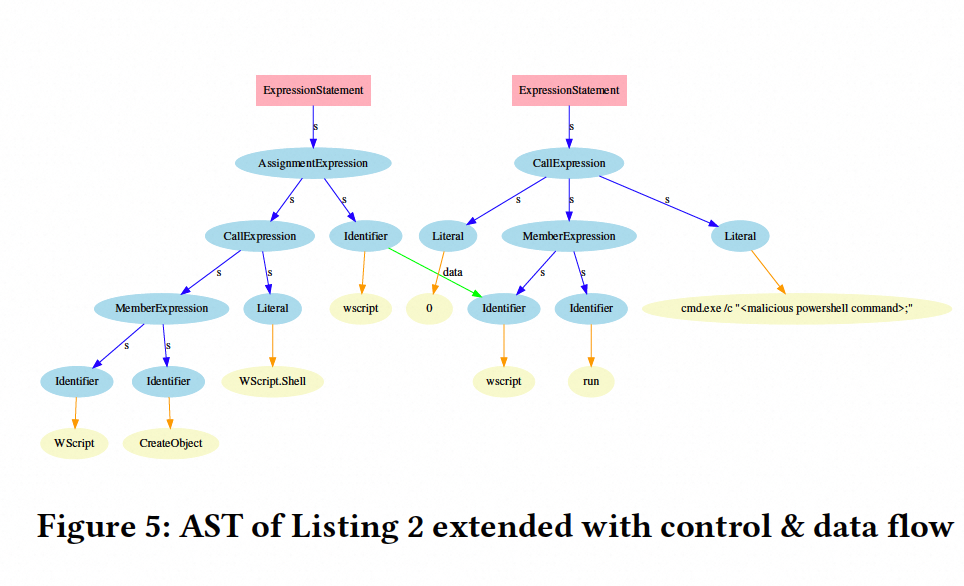
Web安全研究(六)
文章目录 HideNoSeek: Camouflaging(隐藏) Malicious JavaScript in Benign ASTs文章结构Introjs obfuscationmethodologyExample HideNoSeek: Camouflaging(隐藏) Malicious JavaScript in Benign ASTs CCS 2019 CISPA 恶意软件领域,基于学习的系统已经非常流行&am…...

python3 中try 异常调试 raise 异常抛出
一、什么是异常? 异常即是一个事件,该事件会在程序执行过程中发生,影响了程序的正常执行。 一般情况下,在Python无法正常处理程序时就会发生一个异常。 异常是Python对象,表示一个错误。 当Python脚本发生异常时我…...

Java中的序列化是什么?如何实现对象的序列化和反序列化?请解释Serializable接口的作用是什么?请解释transient关键字的作用是什么?为什么会使用它?
Java中的序列化是指将对象转换为字节序列的过程,以便可以在网络上传输或将其保存到持久存储介质中。反序列化则是将字节序列重新转换回对象的过程。Java提供了一种称为序列化(Serialization)的机制来实现对象的序列化和反序列化。 要实现对象…...

二维差分---三维差分算法笔记
文章目录 一.二维差分构造差分二维数组二维差分算法状态dp求b[i][j]数组的二维前缀和图解 二.三维前缀和与差分三维前缀和图解:三维差分核心公式图解:模板题 一.二维差分 给定一个原二维数组a[i][j],若要给a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数…...

D. Divisible Pairs
思路:我们预处理出每个数分别摸上xy的值,用map存一下,然后遍历每个数,如果a b是x的倍数的话,那么他们模x的值相加为x,如果a - b是y的倍数的话,那么他们的模y的值相等。 代码: voi…...

【教程】Kotlin语言学习笔记(二)——数据类型(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【Kotlin语言学习】系列文章 第一章 《认识Kotlin》 第二章 《数据类型》 文章目录 【Kotlin语言学习】系列文章一、基本数据…...

react 插槽
问题开发当中会经常出现组件十分相似的组件,只有一部分是不同的 解决: 父组件:在引用的时候 import { Component } from "react"; import Me from "../me";const name <div>名称</div> class Shoop extends Compone…...

Linux运用fork函数创建进程
fork函数: 函数原型: pid_t fork(void); 父进程调用fork函数创建一个子进程,子进程的用户区父进程的用户区完全一样,但是内核区不完全一样;如父进程的PID和子进程的PID不一样。 返回值: RETURN VALUEO…...

Pytest测试技巧之Fixture:模块化管理测试数据
在 Pytest 测试中,有效管理测试数据是提高测试质量和可维护性的关键。本文将深入探讨 Pytest 中的 Fixture,特别是如何利用 Fixture 实现测试数据的模块化管理,以提高测试用例的清晰度和可复用性。 什么是Fixture? 在 Pytest 中&a…...

设计模式-职责链模式Chain of Responsibility
职责链模式 一、原理和实现二、实现方式1) 使用链表实现2) 使用数组实现3) 扩展 作用:复用和扩展,在实际的项目开发中比较常用。在框架开发中,我们也可以利用它们来提供框架的扩展点,能够让框架的使用者在不修改框架源码的情况下&…...

书生浦语大模型实战营-课程作业(3)
下载sentence_transformer的代码运行情况。sentence_transformer用于embedding(转向量) 本地构建持久化向量数据库。就是把txt和md文件抽取出纯文本,分割成定长(500)后转换成向量,保存到本地,称…...

考研英语单词25
Day 25 bench n.长凳 elastic n.橡皮圈,松紧带 a.灵活的 “e-last 延伸出去” disaster n.灾难,灾祸【disastrous a.灾难性的,极坏的】 deadly a.致命的,极端的,势不两立的 hike n.徒步旅行&…...

计算机网络——08应用层原理
应用层原理 创建一个新的网络 编程 在不同的端系统上运行通过网络基础设施提供的服务,应用进程批次通信如Web Web服务器软件与浏览器软件通信 网络核心中没有应用层软件 网络核心没有应用层功能网络应用只能在端系统上存在 快速网络应用开发和部署 网络应用…...

面试计算机网络框架八股文十问十答第五期
面试计算机网络框架八股文十问十答第五期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)与缓存相关的HTTP请…...
拟合案例1:matlab积分函数拟合详细步骤及源码
本文介绍一下基于matlab实现积分函数拟合的过程。采用的工具是lsqcurvefit和nlinfit两个函数工具。关于包含积分运算的函数,这里可以分为两大类啊。我们用具体的案例来展示:一种是积分运算中不包含这个自变量,如下图的第一个公式,也就是说它这个积分运算只有R和Q这两个待定…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
