线段树解决-----P1161 开灯 P1047 [NOIP2005 普及组] 校门外的树 python解法
# [NOIP2005 普及组] 校门外的树
## 题目描述
某校大门外长度为 l 的马路上有一排树,每两棵相邻的树之间的间隔都是 1 米。我们可以把马路看成一个数轴,马路的一端在数轴 0 的位置,另一端在 l的位置;数轴上的每个整数点,即0,1,2,...,l,都种有一棵树。
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。
## 输入格式
第一行有两个整数,分别表示马路的长度 l 和区域的数目 m。
接下来 m 行,每行两个整数 u, v,表示一个区域的起始点和终止点的坐标。
## 输出格式
输出一行一个整数,表示将这些树都移走后,马路上剩余的树木数量。
## 样例 #1
### 样例输入 #1
```
500 3
150 300
100 200
470 471
```
### 样例输出 #1
```
298
```
## 提示
**【数据范围】**
- 对于 20% 的数据,保证区域之间没有重合的部分。
- 对于 100% 的数据,保证 1≤l≤104,1≤m≤100,0≤u≤v≤l。
**【题目来源】**
NOIP 2005 普及组第二题
n,m=map(int, input().split())
ar=[1 for x in range(n+1)] #生成0~n个共计n+1棵树
for i in range(m):a,b=map(int,input().split())for j in range(a,b+1):ar[j]=0 #范围内挖掉的树置0,若区间有重合也不过是重复置0
print(sum(ar))题目描述
在一条无限长的路上,有一排无限长的路灯,编号为 1,2,3,4,…1,2,3,4,…。
每一盏灯只有两种可能的状态,开或者关。如果按一下某一盏灯的开关,那么这盏灯的状态将发生改变。如果原来是开,将变成关。如果原来是关,将变成开。
在刚开始的时候,所有的灯都是关的。小明每次可以进行如下的操作:
指定两个数,a,t(a 为实数,t 为正整数)。将编号为 ⌊a⌋,⌊2×a⌋,⌊3×a⌋,…,⌊t×a⌋ 的灯的开关各按一次。其中 ⌊k⌋ 表示实数 k 的整数部分。
在小明进行了 n 次操作后,小明突然发现,这个时候只有一盏灯是开的,小明很想知道这盏灯的编号,可是这盏灯离小明太远了,小明看不清编号是多少。
幸好,小明还记得之前的 n 次操作。于是小明找到了你,你能帮他计算出这盏开着的灯的编号吗?
输入格式
第一行一个正整数 n,表示 n 次操作。
接下来有 n 行,每行两个数,ai,ti。其中 ai 是实数,小数点后一定有 6 位,ti 是正整数。
输出格式
仅一个正整数,那盏开着的灯的编号。
输入输出样例
输入 #1复制
3 1.618034 13 2.618034 7 1.000000 21
输出 #1复制
20
说明/提示
记 T=i=1∑nti=t1+t2+t3+⋯+tn。
- 对于 30% 的数据,满足 T≤1000;
- 对于 80% 的数据,满足 T≤200000;
- 对于 100% 的数据,满足 T≤2000000;
- 对于 100% 的数据,满足 n≤5000,1≤ai<1000,1≤ti≤T。
数据保证,在经过 n 次操作后,有且只有一盏灯是开的,不必判错。而且对于所有的 i 来说,ti×ai 的最大值不超过 2000000。
n=int(input())
arr=[0 for i in range(2000000)]
'''
开线段树 关灯状态为0,开灯为1,因为题目说了最后只有一盏灯亮,那么
就找到那一盏灯的编号
'''
for i in range(n):a,t=map(float,input().split())for j in range(1,int(t)+1):#原来亮现在暗if arr[int(j*a)]==0:arr[int(j*a)]=1#原来暗现在亮elif arr[int(j*a)]==1:arr[int(j*a)]=0
print(arr.index(1))相关文章:

线段树解决-----P1161 开灯 P1047 [NOIP2005 普及组] 校门外的树 python解法
# [NOIP2005 普及组] 校门外的树 ## 题目描述 某校大门外长度为 l 的马路上有一排树,每两棵相邻的树之间的间隔都是 1 米。我们可以把马路看成一个数轴,马路的一端在数轴 0 的位置,另一端在 l的位置;数轴上的每个整数点…...

学习总结16
# 【模板】最小生成树 ## 题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 ## 输入格式 第一行包含两个整数 N,M,表示该图共有 N 个结点和 M 条无向边。 接下来 M 行每行包含三个整数 …...
问题:从完整的问题解决过程来看,( )是首要环节。A.理解问题 B.提出假设C.发现问题 D.检验假设 #学习方法#学习方法
问题:从完整的问题解决过程来看,( )是首要环节。A.理解问题 B.提出假设C.发现问题 D.检验假设 A.理解问题 B.提出假设 C.发现问题 参考答案如图所示...

服务器感染了.mallox勒索病毒,如何确保数据文件完整恢复?
导言: 在当今数字化的世界中,恶意软件已成为企业和个人数据安全的一大威胁,其中.mallox勒索病毒是最为恶劣的之一。本文91数据恢复将介绍.mallox勒索病毒的特点,以及如何恢复被其加密的数据文件以及预防措施。 如果您正在经历勒索…...

Android java基础_多态性
一.Android Java基础_多态性 向上转换:只能定义被子类覆写的方法,不能调用在子类中定义的方法。 class Father {private int money; public int getMoney() {return money; }public void setMoney(int money) {this.money money; }public void printInfo() {Syst…...

面试前的准备
目录: 面试前的准备Java程序员校招与社招的区别校招与社招的区别:Java程序员投递简的正确方式投递简历时的误区简历投递时间Java程序员如何应对面试邀约Java程序员如何对公司做背调面试前的技术准备 面试前的准备 Java程序员校招与社招的区别 校招和社招…...

前端架构: 本地调试脚手架的2种方式
一、 调试简单的脚手架方式 假定脚手架名称是 xxx 1 )方式1 在xxx脚手架项目目录的上一级,执行 npm i -g xxx这时候,就可以本地调试脚手架,在前文中已经说明软链的作用参考:https://blog.csdn.net/Tyro_java/article…...

现阶段适用于 单一架构 还是 分布式架构 ?
单体架构: 优势:简单直接,易于理解和开发,适用于小型应用或刚刚开始的项目。劣势:扩展性受限,只能通过增加服务器的数量来提高处理能力;所有模块都部署在一个单独的服务器或容器中,…...

掌握Go并发:Go语言并发编程深度解析
🏷️个人主页:鼠鼠我捏,要死了捏的主页 🏷️系列专栏:Golang全栈-专栏 🏷️个人学习笔记,若有缺误,欢迎评论区指正 前些天发现了一个巨牛的人工智能学习网站,通俗易懂&…...

创建一个多进程服务器和多线程服务器
多进程服务器 #include<myhead.h> #define PORT 8888 //端口号 #define IP "192.168.10.10" //IP地址//定义信号处理函数,用于回收僵尸进程 void handler(int signo) {if(signo SIGCHLD){while(waitpid(-1, NULL, WNOHAN…...
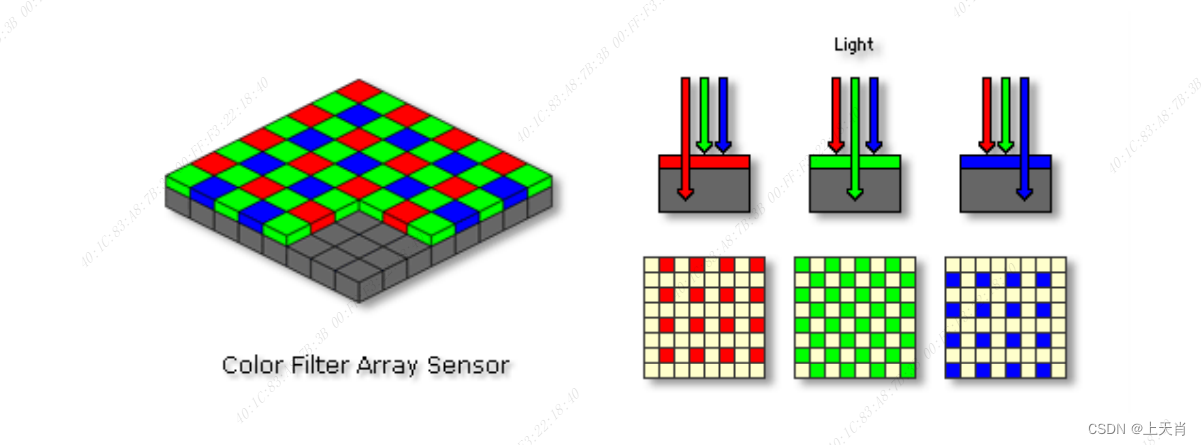
相机图像质量研究(18)常见问题总结:CMOS期间对成像的影响--CFA
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...

18.谈谈你对JSON的理解
JSON 是一种基于文本的轻量级的数据交换格式。它可以被任何的编程语言读取和作为数据格式来传递。 在项目开发中,使用 JSON 作为前后端数据交换的方式。在前端通过将一个符合 JSON 格式的数据结构序列化为 JSON 字符串,然后将它传递到后端,后…...

绝地求生:“觉醒之旅”通行证曝光,西游主题通行证及成长型武器即将上线
随着27赛季即将结束,有关28.1版本的皮肤及通行证内容也被爆料出来,本次通行证为工坊通行证,和去年四圣兽通行证为同一类型,将于2月7日更新至正式服 除了通行证获取工坊币还是可以开箱获取并兑换一些奖励 先看通行证 四个套装应该分…...

JS如何判断普通函数与异步(async)函数
这里可以先打印一下普通函数和异步(async)函数的结构,如下图 可以看出两者原型链,普通函数的原型链指向的是一个函数,异步(async)函数原型链指向的是一个AsyncFunction,这时就会想到…...

ndk-r20b 编译 boost 1.74。
ndk-r20b 编译 boost 1.74,这是 ndk-r20b 支持得最大 boost 版本,再大就没法编译支持了,本文介绍方法是完整编译,不需要完整编译请转移到github,boost for android 得开源项目。 1.74 boost ,安卓上面得版本…...

尚硅谷最新Node.js 学习笔记(四)
目录 八、express框架 8.1、express介绍 8.2、express使用 express下载 express初体验 8.3、express路由 什么是路由? 路由的使用 获取请求参数 获取路由参数 8.4、express响应设置 8.5、express中间件 什么是中间件? 中间件的作用 中间件…...

掌握XGBoost:GPU 加速与性能优化
导言 XGBoost是一种强大的机器学习算法,但在处理大规模数据时,传统的CPU计算可能会变得缓慢。为了提高性能,XGBoost可以利用GPU进行加速。本教程将介绍如何在Python中使用XGBoost进行GPU加速以及性能优化的方法,并提供相应的代码…...
【2024年毕设系列】如何使用Anaconda和Pycharm
【2024年毕设系列】如何使用Anaconda和Pycharm 视频教程地址:【2024毕设系列】Anaconda和Pycharm如何使用_哔哩哔哩 Hi,各位好久不见,这里是肆十二,首先在这里给大伙拜年了。 诸位过完年之后估计又要开始为了大作业和毕业设计头疼…...
Blazor OIDC 单点登录授权实例5 - 独立SSR App (net8 webapp ) 端授权
目录: OpenID 与 OAuth2 基础知识Blazor wasm Google 登录Blazor wasm Gitee 码云登录Blazor OIDC 单点登录授权实例1-建立和配置IDS身份验证服务Blazor OIDC 单点登录授权实例2-登录信息组件wasmBlazor OIDC 单点登录授权实例3-服务端管理组件Blazor OIDC 单点登录授权实例4 …...
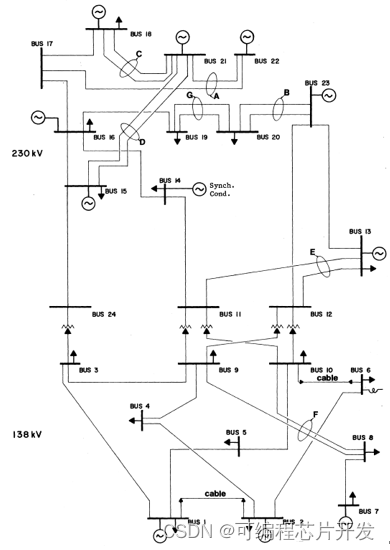
基于蒙特卡洛的电力系统可靠性分析matlab仿真,对比EDNS和LOLP
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 1.课题概述 电力系统可靠性是指电力系统按可接受的质量标准和所需数量不间断地向电力用户供应电力和电能量的能力的量度,包括充裕度和安全性两个方面。发电系统可靠性是指统一并网的全部发电机…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
