OpenCV-36 多边形逼近与凸包
目录
一、多边形的逼近
二、凸包
一、多边形的逼近
findContours后的轮廓信息countours可能过于复杂不平滑,可以用approxPolyDP函数对该多边形曲线做适当近似,这就是轮廓的多边形逼近。
apporxPolyDP就是以多边形去逼近轮廓,采用的是Douglas-Peucker算法(方法名中的DP)
DP算法原理比较简单,核心就是不断去找多边形最远的点加入形成新的多边形,直到最短距离小于指定的精度(阈值)。
approxPolyDP(curve, epsilon, closed[, approxCurvel])
- curve 要逼近的轮廓
- epsilon 即DP算法使用的阈值
- closed 轮廓是否闭合
阈值越大,逼近效果越粗糙;阈值越小,逼近效果越好。
得到的approx本质是一个数组ndarray类型,因此画轮廓的时候需要加上[]变成列表类型。
示例代码如下:
import cv2
import numpy as np
# 导入图片
hand = cv2.imread("hand.png")
# 变为单通道黑白图片
gray = cv2.cvtColor(hand, cv2.COLOR_BGR2GRAY)
# 二值化操作
ret, new_img = cv2.threshold(gray, 150, 255, cv2.THRESH_BINARY)
# 查找轮廓
contours, hierarchy = cv2.findContours(new_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
# 复制一份原图
hand_copy = hand.copy()
# 直接在img_copy上面操作
cv2.drawContours(hand_copy, contours, -1, (0, 0, 255), 2)
# 使用多边形逼近,近似模拟手的轮廓
approx = cv2.approxPolyDP(contours[2], 20, closed=True)
# approx本质上是一个轮廓数据,是一个ndarray类型
print(approx)
print(type(approx))
# 二contours是一个元组/列表类型
# 画出近似逼近的轮廓
cv2.drawContours(hand_copy, [approx], -1, (0, 255, 0), 2)
cv2.imshow("img", np.hstack((hand, hand_copy)))
cv2.waitKey(0)
cv2.destroyAllWindows()输出结果如下:

二、凸包
逼近多边形是轮廓的高度近似,但是有时候,我们希望使用一个多边形的凸包来简化它。 凸包和逼近多边形很像,只不过它是物体最外层的凸多边形。凸包指的是完全包含原有轮廓,并且仅由轮廓上的点所构成的多边形。凸包的每一处都凸的,即在凸包内连接任意两点的直线都在凸包的内部。在凸包内,任意连续三个点的内角小于180°。
convexHull(points[,hull [,clockwise[, returnpoints]]]])
- points 即轮廓
- colckwise 顺时针绘制
示例代码如下:
import cv2
hand = cv2.imread("hand.png")
# 二值化操作
gray = cv2.cvtColor(hand, cv2.COLOR_BGR2GRAY)
# 二值化操作
thresh, binary = cv2.threshold(gray, 150, 255, cv2.THRESH_BINARY)
# 查找轮廓
contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
# 绘制轮廓
cv2.drawContours(hand, contours, 0, (0, 0, 255), 2)
# 多边形逼近
approx = cv2.approxPolyDP(contours[2], 20, True)
# 画出多边形逼近的轮廓
cv2.drawContours(hand, [approx], 0, (0, 0, 255), 2)
# 计算凸包
hull = cv2.convexHull(contours[2])
# 画出凸包
cv2.drawContours(hand, [hull], 0, (255, 0, 0), 2)
cv2.imshow("hand", hand)
cv2.waitKey(0)
cv2.destroyAllWindows()输出结果如下:

相关文章:

OpenCV-36 多边形逼近与凸包
目录 一、多边形的逼近 二、凸包 一、多边形的逼近 findContours后的轮廓信息countours可能过于复杂不平滑,可以用approxPolyDP函数对该多边形曲线做适当近似,这就是轮廓的多边形逼近。 apporxPolyDP就是以多边形去逼近轮廓,采用的是Doug…...

transformer中的QKV是如何得到的?
多头自注意力机制:...

console.log导致内存泄露 打包时自动去掉console.log方法
webpack通过工具:terser 使用前需要先安装一下 vue.config.js const { defineConfig } require(vue/cli-servise); module.exports defineConfig({transpileDependencies:true,terser:{terserOptions:{compress:{drop_console:true,drop_debugger:true,},},},}…...

《合成孔径雷达成像算法与实现》FIgure6.20
% rho_r c/(2*Fr)而不是rho_r c/(2*Bw) % Hsrcf exp函数里忘记乘pi了 clc clear close all参数设置 距离向参数设置 R_eta_c 20e3; % 景中心斜距 Tr 2.5e-6; % 发射脉冲时宽 Kr 20e12; % 距离向调频率 alpha_os_r 1.2; …...
Spring Boot 笔记 015 创建接口_更新文章分类
1.1.1 实体类id增加NotNull注释,并做分组校验 1.1.1.1 定义分组 1.1.1.2 实体类中指定校验项属于哪个分组 如果说某个校验项没有指定分组,默认属于Default分组 分组之间可以继承, A extends B 那么A中拥有B中所有的校验项package com.geji.pojo;import com.faste…...

【Java基础题型】判断是否是回文数
需求:如果给你一个正数x。 如果x是一个回文整数,打印true,否则,返回false 解释: 回文数是指正序(从左到右)和从倒序(从右到左)都是一样的整数数字。 eg.121是回文数,123不是,2112是回文数&…...
)
Linux paste命令教程:并行合并文件的利器(附案例详解和注意事项)
Linux paste命令介绍 paste 是一个在 Unix 或 Linux 操作系统中非常有用的命令。它用于通过在标准输出中输出由每个指定文件的行组成的行,以制表符为分隔符,来水平(并行)合并文件。 Linux paste命令适用的Linux版本 paste 命令…...
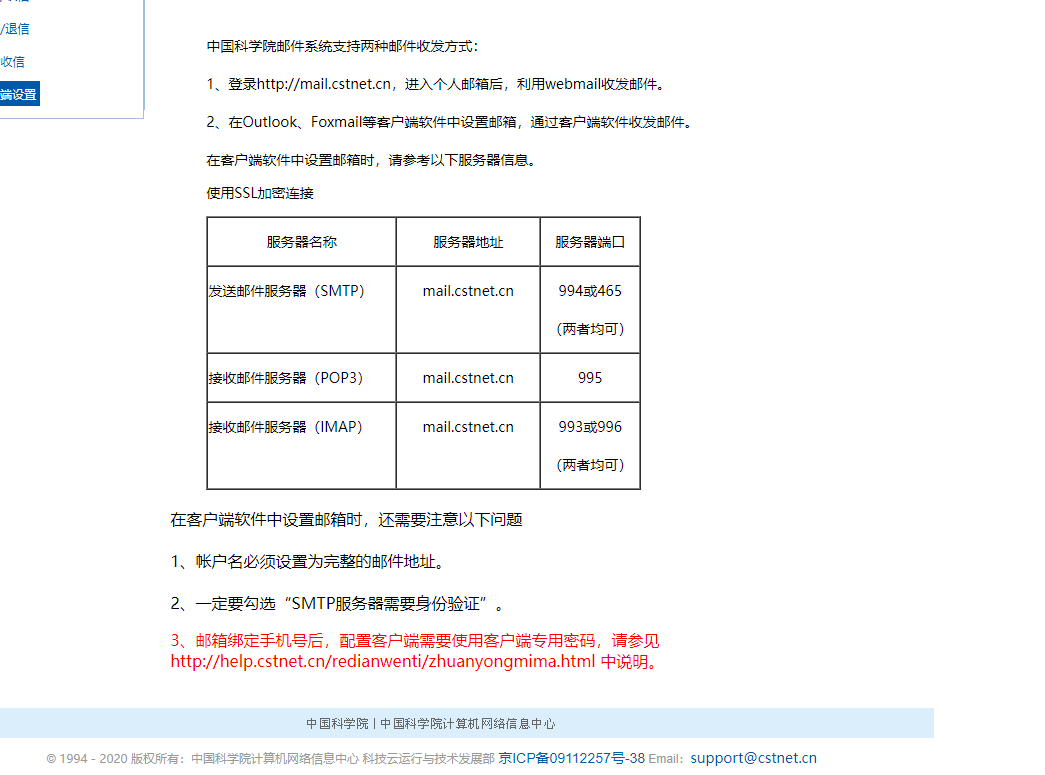
用163邮箱或者outlook接收国科大邮箱的邮件
使用如图下路径,创建一个新的密码,用于在163大师邮箱或者outlook登录即可 如果不行,则需要手动配置邮箱服务器 参考网址:中国科学院邮件系统帮助中心...
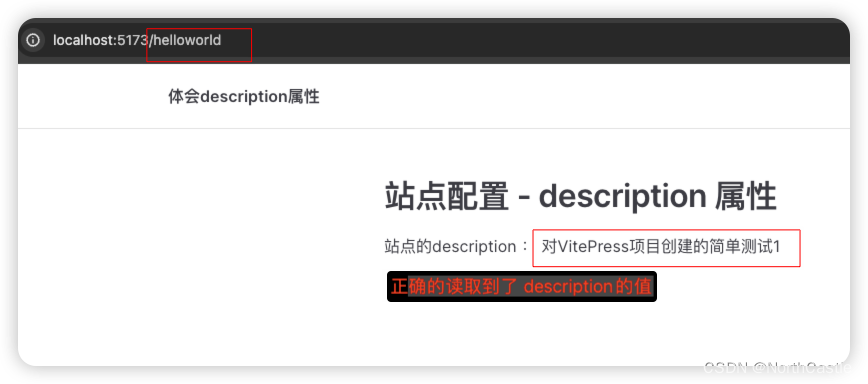
VitePress-15- 配置- description 的作用详解
作用描述 1、descriptioin 是站点的描述, 会被解析为 html 页面的 <meta name"description" content "xxx"> 标签 。2、description 本身就是 <meta> 标签的一种,不会在页面上展示出来, 仅仅是作为页面的一…...
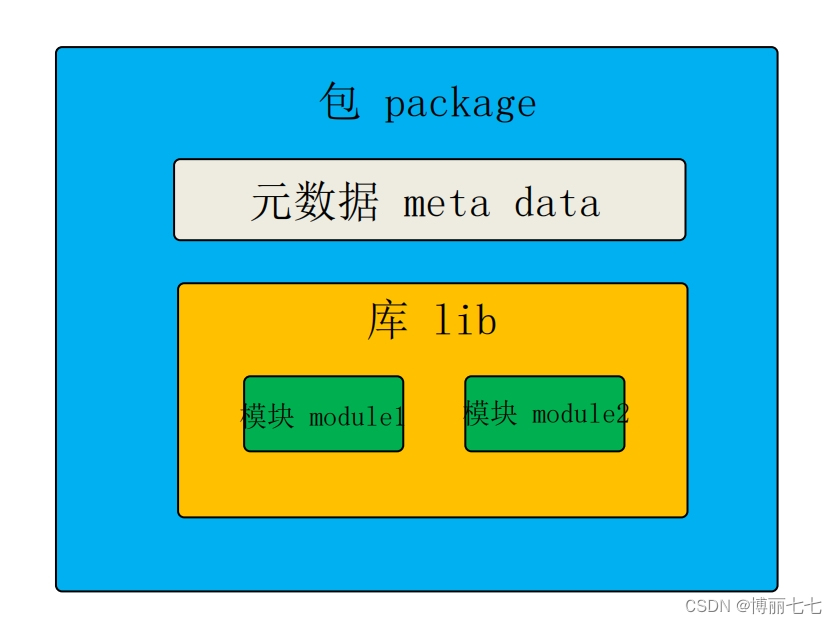
寒假学习记录17:包管理器(包管理工具)
概念 包(package) 包含元数据的库,这些元数据包括:名称,描述,git主页,许可证协议,作者,依赖..... 库(library,简称lib) 以一个或多个模…...

【AIGC】Stable Diffusion的常见错误
Stable Diffusion 在使用过程中可能会遇到各种各样的错误。以下是一些常见的错误以及可能的解决方案: 模型加载错误:可能出现模型文件损坏或缺失的情况。解决方案包括重新下载模型文件,确保文件完整并放置在正确的位置。 依赖项错误&#x…...

线段树解决-----P1161 开灯 P1047 [NOIP2005 普及组] 校门外的树 python解法
# [NOIP2005 普及组] 校门外的树 ## 题目描述 某校大门外长度为 l 的马路上有一排树,每两棵相邻的树之间的间隔都是 1 米。我们可以把马路看成一个数轴,马路的一端在数轴 0 的位置,另一端在 l的位置;数轴上的每个整数点…...

学习总结16
# 【模板】最小生成树 ## 题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 ## 输入格式 第一行包含两个整数 N,M,表示该图共有 N 个结点和 M 条无向边。 接下来 M 行每行包含三个整数 …...
问题:从完整的问题解决过程来看,( )是首要环节。A.理解问题 B.提出假设C.发现问题 D.检验假设 #学习方法#学习方法
问题:从完整的问题解决过程来看,( )是首要环节。A.理解问题 B.提出假设C.发现问题 D.检验假设 A.理解问题 B.提出假设 C.发现问题 参考答案如图所示...

服务器感染了.mallox勒索病毒,如何确保数据文件完整恢复?
导言: 在当今数字化的世界中,恶意软件已成为企业和个人数据安全的一大威胁,其中.mallox勒索病毒是最为恶劣的之一。本文91数据恢复将介绍.mallox勒索病毒的特点,以及如何恢复被其加密的数据文件以及预防措施。 如果您正在经历勒索…...

Android java基础_多态性
一.Android Java基础_多态性 向上转换:只能定义被子类覆写的方法,不能调用在子类中定义的方法。 class Father {private int money; public int getMoney() {return money; }public void setMoney(int money) {this.money money; }public void printInfo() {Syst…...

面试前的准备
目录: 面试前的准备Java程序员校招与社招的区别校招与社招的区别:Java程序员投递简的正确方式投递简历时的误区简历投递时间Java程序员如何应对面试邀约Java程序员如何对公司做背调面试前的技术准备 面试前的准备 Java程序员校招与社招的区别 校招和社招…...

前端架构: 本地调试脚手架的2种方式
一、 调试简单的脚手架方式 假定脚手架名称是 xxx 1 )方式1 在xxx脚手架项目目录的上一级,执行 npm i -g xxx这时候,就可以本地调试脚手架,在前文中已经说明软链的作用参考:https://blog.csdn.net/Tyro_java/article…...

现阶段适用于 单一架构 还是 分布式架构 ?
单体架构: 优势:简单直接,易于理解和开发,适用于小型应用或刚刚开始的项目。劣势:扩展性受限,只能通过增加服务器的数量来提高处理能力;所有模块都部署在一个单独的服务器或容器中,…...

掌握Go并发:Go语言并发编程深度解析
🏷️个人主页:鼠鼠我捏,要死了捏的主页 🏷️系列专栏:Golang全栈-专栏 🏷️个人学习笔记,若有缺误,欢迎评论区指正 前些天发现了一个巨牛的人工智能学习网站,通俗易懂&…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
