【matalab】基于Octave的信号处理与滤波分析案例
 一、基于Octave的信号处理与滤波分析案例
一、基于Octave的信号处理与滤波分析案例
GNU Octave是一款开源软件,类似于MATLAB,广泛用于数值计算和信号处理。
一个简单的信号处理与滤波分析案例,说明如何在Octave中生成一个有噪声的信号,并设计一个滤波器来去除噪声。
首先,确保安装了Octave。可以从Octave官网下载并安装:GNU Octave
案例步骤如下:
1. 生成一个简单的正弦波信号。
2. 添加噪声。
3. 设计和应用一个低通滤波器。
以下是Octave的代码:
pkg load signal; % 加载 signal 包% 1. 生成一个简单的正弦波信号
Fs = 1000; % 采样率
t = 0:1/Fs:1; % 时间向量
f = 5; % 信号频率
A = 0.7; % 信号振幅
signal = A * sin(2*pi*f*t);
% 2. 添加噪声
noise_amplitude = 1;
noisy_signal = signal + noise_amplitude * randn(size(t)); % 带噪声的信号
% 3. 设计和应用一个低通滤波器
fc = 10; % 截止频率
[b, a] = butter(5, fc/(Fs/2)); % 使用5阶巴特沃斯滤波器
filtered_signal = filter(b, a, noisy_signal); % 应用滤波器
% 绘制结果
subplot(3, 1, 1);
plot(t, signal);
title('Original Signal');
subplot(3, 1, 2);
plot(t, noisy_signal);
title('Noisy Signal');
subplot(3, 1, 3);
plot(t, filtered_signal);
title('Filtered Signal');
% 需要额外读取和播放的命令
%sound(signal, Fs); % 播放原始信号
%sound(noisy_signal, Fs); % 播放含噪声的信号
%sound(filtered_signal, Fs); % 播放滤波后的信号以上脚本中,首先创建了一个简单的单频正弦信号。然后,在这个信号上添加了高斯白噪声,模拟真实世界的信号干扰。随后,设计了一个5阶巴特沃斯低通滤波器,以去除高于10 Hz频率的噪声。最后用subplot来绘制原始信号、带噪声的信号以及滤波后的信号的图形。
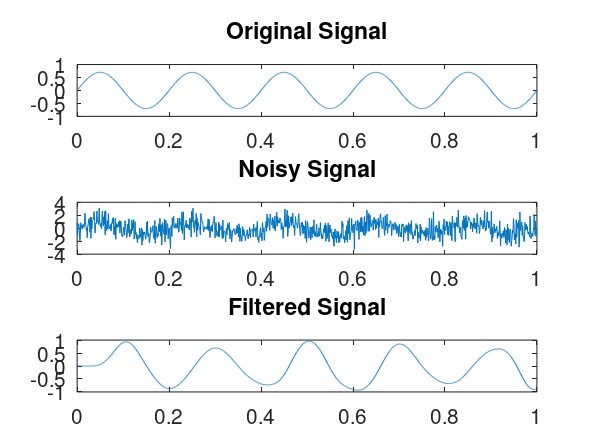
这个滤波器设计是基于应用滤波器的标准`filter`函数。可以通过修改截止频率`fc`来适配不同情况下的噪声特性。
在Octave中运行以上代码,可以看到这三个信号的对比,它展示了滤波器如何有效地移除噪声并保留原始信号的形状。滤波器设计和参数的选择将直接影响过滤效果,所以可能需要根据特定情况调整参数。
二、安装使用Octave运行这个案例
安装和使用Octave运行上述案例需要几个步骤:
安装Octave
Windows:
1. 前往Octave官网下载页面:Download
2. 选择适合的操作系统的安装程序(例如:"octave-x.x.x-w64-installer.exe" 对于64位Windows系统)。
3. 下载并运行安装程序,安装Octave并遵循安装向导指示。
macOS:
1. 访问Octave官方网站下载页面或使用Homebrew。
2. 如果使用下载页面,请选择适合macOS的安装包下载。
3. 如果使用Homebrew,则打开终端并运行以下命令:
brew install octaveLinux:
对于大多数基于Debian的系统(如Ubuntu),可以使用APT获取Octave:
sudo apt update
sudo apt install octave如果在尝试加载 Octave 的信号处理包 signal 时(pkg load signal;)出现错误,这意味着该包没有安装在系统中。在这种情况下,需要首先安装 signal 包。在 Linux 系统上,可以通过以下步骤安装它:
1. 打开终端。
2. 启动 Octave 交互界面,只需输入 octave 并回车。
3. 在 Octave 提示符下安装 signal 包,使用下列命令:
pkg install -forge signal 这个命令会从 Octave Forge 下载并安装 signal 包。
如果在安装过程中遇到权限问题,可能需要使用 sudo 或以超级用户权限运行 Octave。在某些 Linux 分发版(例如 Ubuntu)中,还可以通过系统的包管理器安装 Octave 包,如使用 apt:
sudo apt-get install octave-signal对于基于Fedora的系统:
sudo dnf install octave对于其他发行版,根据系统的包管理器来安装Octave。
运行Octave案例
1. 安装完成后,打开Octave GUI 或终端界面。
2. 在界面中,可以直接输入命令执行,或将上述案例的代码保存为`.m`文件(比如命名为`signal_filtering_example.m`)。
3. 如果将代码保存为文件,可以直接在Octave界面中使用`cd`命令切换到该文件所在的目录,然后通过输入文件名不带扩展名来运行脚本,如:
cd /path/to/directorysignal_filtering_example4. 如果想直接在Octave命令窗口中运行,可以逐行输入代码或使用剪贴板复制粘贴整个代码块。
5. 运行脚本后,Octave将会按照指定的命令绘制相应的信号图。
如果需要Octave支持声音播放,在一些操作系统中可能需要额外的配置或安装额外的软件包。如果遇到问题,请参阅Octave的官方文档或寻求社区的帮助。
三、Octave与MATLAB
GNU Octave是一个开源的数值计算软件,它与Matlab非常相似,因此它可以用来作为学习Matlab语言的一个免费资源。
提供的案例代码基本上也可以在MATLAB中运行,因为Octave与MATLAB非常相似,很多基本的函数和语法是通用的。但是,有时可能会存在一些细微的差异,比如在某些函数的参数处理上,或者是图形界面的展现上。
如果在MATLAB中运行这段代码,应该会得到与在Octave中相似的结果。这段代码使用了标准的信号处理函数,如`sin`、`randn`和`filter`,这些在MATLAB的信号处理工具箱中也是存在的。
要在MATLAB中运行,只需复制和粘贴这段代码到MATLAB的命令窗口或者一个`.m`文件中,然后执行即可。如果MATLAB环境中信号处理工具箱(Signal Processing Toolbox)没有安装或者版本不兼容,那么可能会在执行某些信号处理函数时遇到问题。就这个具体示例而言,所有使用的函数都是MATLAB基础函数集的一部分,不需要额外的工具箱。

相关文章:

【matalab】基于Octave的信号处理与滤波分析案例
一、基于Octave的信号处理与滤波分析案例 GNU Octave是一款开源软件,类似于MATLAB,广泛用于数值计算和信号处理。 一个简单的信号处理与滤波分析案例,说明如何在Octave中生成一个有噪声的信号,并设计一个滤波器来去除噪声。 首…...

Elasticsearch:特定领域的生成式 AI - 预训练、微调和 RAG
作者:来自 Elastic Steve Dodson 有多种策略可以将特定领域的知识添加到大型语言模型 (LLM) 中,并且作为积极研究领域的一部分,正在研究更多方法。 对特定领域数据集进行预训练和微调等方法使 LLMs 能够推理并生成特定领域语言。 然而&#…...

HarmonyOS—UI 开发性能提升的推荐方法
开发者若使用低性能的代码实现功能场景可能不会影响应用的正常运行,但却会对应用的性能造成负面影响。本章节列举出了一些可提升性能的场景供开发者参考,以避免应用实现上带来的性能劣化。 使用数据懒加载 开发者在使用长列表时,如果直接采用…...

84 CTF夺旗-PHP弱类型异或取反序列化RCE
目录 案例1:PHP-相关总结知识点-后期复现案例2:PHP-弱类型对比绕过测试-常考点案例3:PHP-正则preg_match绕过-常考点案例4:PHP-命令执行RCE变异绕过-常考点案例5:PHP-反序列化考题分析构造复现-常考点涉及资源…...
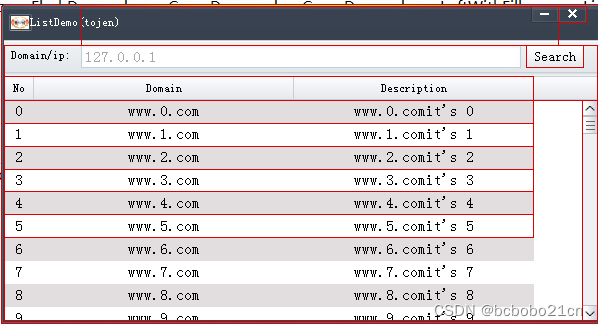
Duilib List 控件学习
这是自带的一个示例; 一开始运行的时候List中是空的,点击Search按钮以后就填充列表框; 先看一下列表框列头是在xml文件中形成的; <List name="domainlist" bkcolor="#FFFFFFFF" ... menu="true"> <ListHeader height="24…...

详细了解Node.js的配置与使用!
详细了解Node.js的配置与使用! Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。它允许开发者在服务器端运行 JavaScript,从而实现全栈 JavaScript 开发。本文将介绍 Node.js 的配置和 npm 的应用。 一、Node.js 配置 下载与安装 首先&…...

OpenCV 移动最小二乘图像变形
文章目录 一、简介二、实现代码三、实现效果参考文献一、简介 在现实生活中,我们常常应用一些刚性的变换来实现物体的旋转平移,对于非刚性的变换我们都没有在意,其实这种变换也是无处不在的,如我们经常看的动画就可以通过一些非刚性的变换达到一些非常夸张的效果。这里,我…...

【深度学习】S2 数学基础 P4 概率论
目录 基本概率论概率论公理随机变量 多个随机变量联合概率条件概率贝叶斯定理求和法则独立性 期望与方差小结 基本概率论 机器学习本质上,就是做出预测。而概率论提供了一种量化和表达不确定性水平的方法,可以帮助我们量化对某个结果的确定性程度。 在…...

跟我学c++中级篇——静态多态
一、多态 Polymorphism,多态。学习过c的人如果不知道多态,基本上就是打入c内部的C程序员了。在前边曾经对多态进行过分析,对其中的虚函数(虚表等)也进行过较为详细的说明。 多态其实非常好理解,不要硬扣书…...
)
设计模式--桥接模式(Bridge Pattern)
桥接模式(Bridge Pattern)是一种结构型设计模式,它主要是用于将抽象部分与实现部分分离,使它们可以独立地变化。 桥接模式主要包含以下几个角色: Abstraction(抽象类):定义抽象类的…...
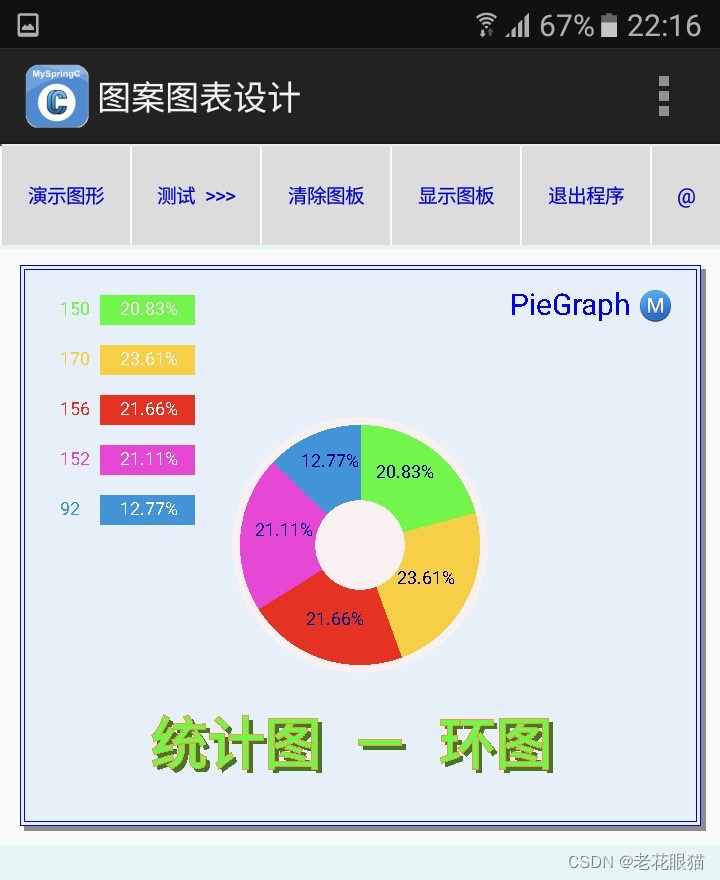
统计图饼图绘制方法(C语言)
统计图饼图绘制方法(C语言) 常用的统计图有条形图、柱形图、折线图、曲线图、饼图、环形图、扇形图。 前几类图比较容易绘制,饼图绘制较难。今值此介绍饼图的绘制方法。 本方法采用C语言的最基本功能: ( 1.)…...

洛谷C++简单题小练习day12—寻找最小值小程序
day12--寻找最小值--2.16 习题概述 题目描述 给出 n 和 n 个整数 ai,求这 n 个整数中最小值是什么。 输入格式 第一行输入一个正整数 n,表示数字个数。 第二行输入 n 个非负整数,表示 1,2…a1,a2…an,以空格隔开。 …...

相机图像质量研究(13)常见问题总结:光学结构对成像的影响--鬼影
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...
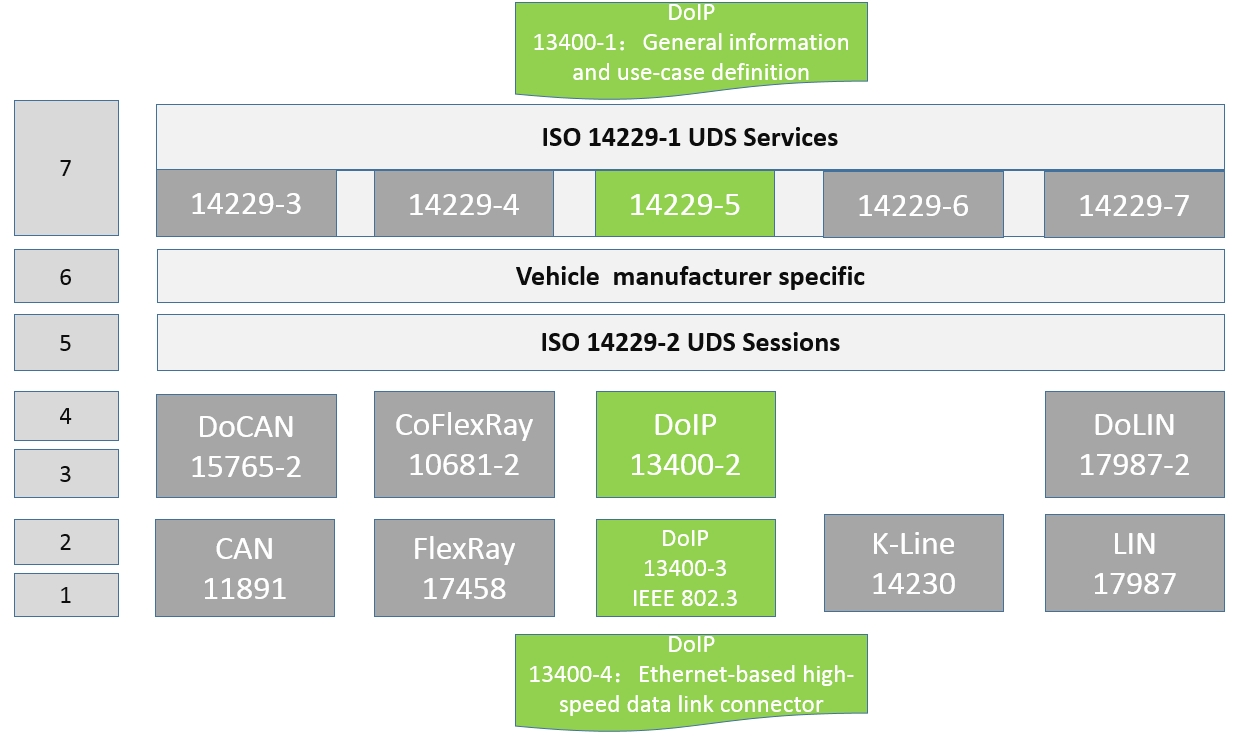
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师(Wechat:gongkenan2013)。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自己。江湖一碗茶,…...

掘根宝典之C++包含对象的类,私有继承,保护继承,三大继承方式总结
包含对象成员的类 包含,组合和层次化:一个类里面的类成员之一是个类对象 我们来看个例子 #include<iostream> using namespace std; class AA { private:int a_; public:AA(int a):a_(a){}void A(){cout << a_ << endl;} }; class …...

第六篇:MySQL图形化管理工具
经过前五篇的学习,对于数据库这门技术的理解,我们已经在心中建立了一个城堡大致的雏形,通过命令行窗口(cmd)快速上手了【SQL语法-DDL-数据定义语言】等相关命令 道阻且长,数据库技术这一宝藏中还有数不清的…...

计算机网络——12DNS
DNS DNS的必要性 IP地址标识主机、路由器但IP地址不好记忆,不便于人类用使用(没有意义)人类一般倾向于使用一些有意义的字符串来标识Internet上的设备存在着“字符串”——IP地址的转换的必要性人类用户提供要访问机器的“字符串”名称由DN…...
vue3-应用规模化-工具链
工具链 项目脚手架 Vite Vite 是一个轻量级的、速度极快的构建工具,对 Vue SFC 提供第一优先级支持。作者是尤雨溪,同时也是 Vue 的作者! 要使用 Vite 来创建一个 Vue 项目,非常简单: (推荐)…...
EasyExcel动态列导出
测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/tree/master/src/test/java/com/xiaobai/easyexcel/dynamiccolumn 官方文档:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 一、实现方式 1、根据需要导出的列…...

JAVA面试题11
什么是Java的访问修饰符,并列出它们的作用。 Java的访问修饰符包括public、private、protected和默认。它们的作用如下: public: 可以被任何其他类访问。 private: 只能被所在类访问,其他类无法访问。 protected: 可以被所在类和同一个包中的…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
