redis为什么使用跳跃表而不是树
Redis中支持五种数据类型中有序集合Sorted Set的底层数据结构使用的跳跃表,为何不使用其他的如平衡二叉树、b+树等数据结构呢?
1,redis的设计目标、性能需求:
redis是高性能的非关系型(NoSQL)内存键值数据库,它以其快速的操作速度而闻名。
读取速度:Redis能实现极高的读取速度,据官方测试报告,可以达到每秒约110,000次读取操作。
写入速度:与读取相比,写入速度略低,但仍然相当可观,官方数据显示,Redis的写入速度大约是每秒81,000次操作。
类似产品如Memcached等,无法达到如此性能。
2,有序集合都可以借助什么数据结构及其基本原理
有序集合需求:自然有序,查找高速,支持范围查找
2.1,传统数组/链表+排序
数组或链表可以存储数据,可以新增或修改数据后重新排序,
而在集合排序方面,最快的归并排序也需要O(NlongN)的时间复杂度。
时间不够快,但实现、使用方面简单

2.2,跳跃表(链表的优化–链表+多级索引)
跳跃表最早是由William Pugh在1990年提出的,被用来代替平衡树(如AVL树和红黑树)来实现有序集合。跳跃表的查询复杂度为O(log n),与平衡树相当,但由于其实现较为简单,所以在实际使用中比平衡树更加高效。
例:查找90

增加指针,让指针指向远处个节点,
如上图,共四层,最底层(原链表L1)节点是10 - 20 - 30 -… - 120,中间层L2增加节点10 - 30 - 40 - 60 - 80 - 100 - 120,L2上层L3增加节点10 - 40 - 80 - 120 最高层10 - 120
这样形成三个新的链表,但它包含的节点个数只有原来的一部分;
当我们查找数据之时,先沿着这个最高层链表进行查找。当碰到比待查数据大的节点时,再到中间层,最后回到原来的链表中进行查找。
如查找90,共经历6步。
过程类似二分查找,时间复杂度支持平均O(logN),最坏O(N)的节点查找,还可以顺序性操作来批量处理节点。
2.3,平衡二叉树/红黑树

平衡二叉树的查询复杂度为O(logN),但新增、删除需要调整保持平衡,实现相对复杂;
范围查询方面,平衡二叉树支持范围查询,但是这这种数据结构要范围查找要往回找,即回溯到父结点,而B+树的叶子结点的指针的效率则更高
2.4,B+树
B+ Tree是一种经典的多路平衡查找树,它通常被用来实现磁盘上的数据结构。在B+ Tree中,每个节点可以包含多个键值对,而且所有叶子节点都被连接成一个链表。B+ Tree的查询复杂度也是O(log n),但由于其实现较为复杂,所以在实际使用中通常用于数据库系统等需要高效读写的场景中。

3,跳跃表与平衡树的实现

//redis源码中跳跃表结构的实现:
/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {sds ele;double score;//分值struct zskiplistNode *backward;//后退指针//层struct zskiplistLevel {struct zskiplistNode *forward;//前进指针unsigned long span;//跨度} level[];
} zskiplistNode;
如图,一个跳表节点,有level数组,每个元素都有一个指向其他节点的指针,可以通过这些层来加快访问速度
3.1使用java实现跳跃表:
import java.util.Random;class Node {int key;int value;Node[] next;public Node(int level, int key, int value) {this.key = key;this.value = value;this.next = new Node[level + 1];}
}public class SkipList {private static final int MAX_LEVEL = 16; // 最大层数private int level; // 当前层数private Node head; // 头节点private Random random; // 用于生成随机层数public SkipList() {this.level = 0;this.head = new Node(MAX_LEVEL, 0, 0);this.random = new Random();}// 生成随机层数private int randomLevel() {int level = 0;while (level < MAX_LEVEL && random.nextDouble() < 0.5) {level++;}return level;}// 插入节点public void insert(int key, int value) {Node[] update = new Node[MAX_LEVEL + 1];Node current = head;for (int i = level; i >= 0; i--) {while (current.next[i] != null && current.next[i].key < key) {current = current.next[i];}update[i] = current;}int newLevel = randomLevel();if (newLevel > level) {for (int i = level + 1; i <= newLevel; i++) {update[i] = head;}level = newLevel;}Node newNode = new Node(newLevel, key, value);for (int i = 0; i <= newLevel; i++) {newNode.next[i] = update[i].next[i];update[i].next[i] = newNode;}}// 查找节点public Node search(int key) {Node current = head;for (int i = level; i >= 0; i--) {while (current.next[i] != null && current.next[i].key < key) {current = current.next[i];}}if (current.next[0] != null && current.next[0].key == key) {return current.next[0];}return null;}// 删除节点public void delete(int key) {Node[] update = new Node[MAX_LEVEL + 1];Node current = head;for (int i = level; i >= 0; i--) {while (current.next[i] != null && current.next[i].key < key) {current = current.next[i];}update[i] = current;}if (current.next[0] != null && current.next[0].key == key) {for (int i = 0; i <= level; i++) {if (update[i].next[i] != current.next[i]) {break;}update[i].next[i] = current.next[i];}while (level > 0 && head.next[level] == null) {level--;}}}// 打印跳跃表public void printSkipList() {for (int i = level; i >= 0; i--) {Node current = head;System.out.print("Level " + i + ": ");while (current.next[i] != null) {System.out.print(current.next[i].key + " ");current = current.next[i];}System.out.println();}}public static void main(String[] args) {SkipList skipList = new SkipList();skipList.insert(3, 30);skipList.insert(1, 10);skipList.insert(2, 20);skipList.insert(4, 40);System.out.println("Skip List after insertion:");skipList.printSkipList();int searchKey = 2;Node searchResult = skipList.search(searchKey);if (searchResult != null) {System.out.println("Node with key " + searchKey + " found. Value: " + searchResult.value);} else {System.out.println("Node with key " + searchKey + " not found.");}int deleteKey = 2;skipList.delete(deleteKey);System.out.println("Skip List after deletion of key " + deleteKey + ":");skipList.printSkipList();}
}3.2使用java实现平衡二叉树(AVLTree):
class Node {int key, height;Node left, right;public Node(int key) {this.key = key;this.height = 1;}
}public class AVLTree {private Node root;// 获取节点的高度private int height(Node node) {return (node == null) ? 0 : node.height;}// 获取树的平衡因子private int getBalance(Node node) {return (node == null) ? 0 : height(node.left) - height(node.right);}// 更新节点的高度private void updateHeight(Node node) {node.height = 1 + Math.max(height(node.left), height(node.right));}// 执行右旋转private Node rightRotate(Node y) {Node x = y.left;Node T2 = x.right;// 执行旋转x.right = y;y.left = T2;// 更新高度updateHeight(y);updateHeight(x);return x;}// 执行左旋转private Node leftRotate(Node x) {Node y = x.right;Node T2 = y.left;// 执行旋转y.left = x;x.right = T2;// 更新高度updateHeight(x);updateHeight(y);return y;}// 插入节点public Node insert(Node node, int key) {if (node == null) {return new Node(key);}// 执行标准的BST插入if (key < node.key) {node.left = insert(node.left, key);} else if (key > node.key) {node.right = insert(node.right, key);} else {// 相等的键不允许插入return node;}// 更新节点的高度updateHeight(node);// 获取平衡因子int balance = getBalance(node);// 进行平衡操作// 左重,需要右旋转if (balance > 1 && key < node.left.key) {return rightRotate(node);}// 右重,需要左旋转if (balance < -1 && key > node.right.key) {return leftRotate(node);}// 左右,先左旋转后右旋转if (balance > 1 && key > node.left.key) {node.left = leftRotate(node.left);return rightRotate(node);}// 右左,先右旋转后左旋转if (balance < -1 && key < node.right.key) {node.right = rightRotate(node.right);return leftRotate(node);}// 不需要平衡操作,直接返回节点return node;}// 插入节点的公共接口public void insert(int key) {root = insert(root, key);}// 打印中序遍历结果private void inOrderTraversal(Node node) {if (node != null) {inOrderTraversal(node.left);System.out.print(node.key + " ");inOrderTraversal(node.right);}}// 打印中序遍历结果的公共接口public void inOrderTraversal() {inOrderTraversal(root);System.out.println();}public static void main(String[] args) {AVLTree avlTree = new AVLTree();// 插入节点avlTree.insert(10);avlTree.insert(20);avlTree.insert(30);avlTree.insert(15);avlTree.insert(5);// 打印中序遍历结果System.out.println("Inorder traversal of the AVL tree:");avlTree.inOrderTraversal();}
}3.3java实现B+树:
import java.util.ArrayList;
import java.util.List;class BPlusTree {private BPlusNode root;private int order;public BPlusTree(int order) {this.root = new BPlusLeafNode();this.order = order;}public void insert(int key, String value) {root = root.insert(key, value);}public String search(int key) {return root.search(key);}public void printTree() {root.print();}// B+树节点抽象类abstract static class BPlusNode {List<Integer> keys;BPlusNode() {this.keys = new ArrayList<>();}abstract BPlusNode insert(int key, String value);abstract String search(int key);abstract void print();}// B+树叶子节点类static class BPlusLeafNode extends BPlusNode {List<String> values;BPlusLeafNode next; // 用于连接叶子节点形成链表BPlusLeafNode() {this.values = new ArrayList<>();this.next = null;}@OverrideBPlusNode insert(int key, String value) {int index = 0;while (index < keys.size() && keys.get(index) < key) {index++;}keys.add(index, key);values.add(index, value);// 检查是否需要分裂if (keys.size() > order) {int splitIndex = keys.size() / 2;BPlusLeafNode newLeaf = new BPlusLeafNode();// 将一半的键和值移至新节点newLeaf.keys.addAll(keys.subList(splitIndex, keys.size()));newLeaf.values.addAll(values.subList(splitIndex, values.size()));keys.subList(splitIndex, keys.size()).clear();values.subList(splitIndex, values.size()).clear();// 调整叶子节点链表newLeaf.next = next;next = newLeaf;return newLeaf;}return this;}@OverrideString search(int key) {int index = 0;while (index < keys.size() && keys.get(index) <= key) {if (keys.get(index) == key) {return values.get(index);}index++;}return null;}@Overridevoid print() {System.out.print("Leaf Node: ");for (int i = 0; i < keys.size(); i++) {System.out.print("(" + keys.get(i) + ", " + values.get(i) + ") ");}System.out.println();}}// B+树内部节点类static class BPlusInternalNode extends BPlusNode {List<BPlusNode> children;BPlusInternalNode() {this.children = new ArrayList<>();}@OverrideBPlusNode insert(int key, String value) {int index = 0;while (index < keys.size() && keys.get(index) < key) {index++;}BPlusNode child = children.get(index);BPlusNode newChild = child.insert(key, value);if (newChild != child) {keys.add(index, newChild.keys.get(0));children.add(index + 1, newChild);if (keys.size() > order) {int splitIndex = keys.size() / 2;BPlusInternalNode newInternal = new BPlusInternalNode();// 将一半的键和子节点移至新节点newInternal.keys.addAll(keys.subList(splitIndex, keys.size()));newInternal.children.addAll(children.subList(splitIndex + 1, children.size()));keys.subList(splitIndex, keys.size()).clear();children.subList(splitIndex + 1, children.size()).clear();return newInternal;}}return this;}@OverrideString search(int key) {int index = 0;while (index < keys.size() && keys.get(index) <= key) {index++;}return children.get(index).search(key);}@Overridevoid print() {System.out.print("Internal Node: ");for (int i = 0; i < keys.size(); i++) {System.out.print(keys.get(i) + " ");}System.out.println();for (BPlusNode child : children) {child.print();}}}public static void main(String[] args) {BPlusTree bPlusTree = new BPlusTree(3);bPlusTree.insert(10, "Value10");bPlusTree.insert(20, "Value20");bPlusTree.insert(5, "Value5");bPlusTree.insert(6, "Value6");bPlusTree.insert(12, "Value12");bPlusTree.insert(30, "Value30");System.out.println("B+ Tree after insertion:");bPlusTree.printTree();int searchKey = 12;String searchResult = bPlusTree.search(searchKey);if (searchResult != null) {System.out.println("Value for key " + searchKey + ": " + searchResult);} else {System.out.println("Key " + searchKey + " not found.");}}
}4,Redis的作者 @antirez 的原话与总结
There are a few reasons:
1、They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.
2、A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.
3、They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.
主要是从内存占用、对范围查找的支持、实现难易程度这三方面总结的原因,
简单翻译一下:
1、它们不是非常内存密集型的。基本上由你决定。改变关于节点具有给定级别数的概率的参数将使其比 btree 占用更少的内存。
2、Zset 经常需要执行 ZRANGE 或 ZREVRANGE 的命令,即作为链表遍历跳表。通过此操作,跳表的缓存局部性至少与其他类型的平衡树一样好。
3、它们更易于实现、调试等。例如,由于跳表的简单性,我收到了一个补丁(已经在Redis master中),其中扩展了跳表,在 O(log(N) 中实现了 ZRANK。它只需要对代码进行少量修改。
跳跃表的优势:
1,时间复杂度方面:大部分情况下,跳跃表的效率和平衡树媲美;
2,算法实现方面:跳跃表的实现比平衡树、b+树更为简单;
3,范围查找方面,跳表比平衡树操作要简单,平衡树需要回溯到父结点,条表可以做到 O(logn) 的时间复杂度定位区间的起点,然后在原始链表中顺序往后遍历;
4,对于小数据集的性能: 在某些场景下,跳表在小数据集上的性能可能优于B+树。跳表的查询操作在某些情况下可能更迅速。
相关文章:

redis为什么使用跳跃表而不是树
Redis中支持五种数据类型中有序集合Sorted Set的底层数据结构使用的跳跃表,为何不使用其他的如平衡二叉树、b树等数据结构呢? 1,redis的设计目标、性能需求: redis是高性能的非关系型(NoSQL)内存键值数据…...

【matalab】基于Octave的信号处理与滤波分析案例
一、基于Octave的信号处理与滤波分析案例 GNU Octave是一款开源软件,类似于MATLAB,广泛用于数值计算和信号处理。 一个简单的信号处理与滤波分析案例,说明如何在Octave中生成一个有噪声的信号,并设计一个滤波器来去除噪声。 首…...

Elasticsearch:特定领域的生成式 AI - 预训练、微调和 RAG
作者:来自 Elastic Steve Dodson 有多种策略可以将特定领域的知识添加到大型语言模型 (LLM) 中,并且作为积极研究领域的一部分,正在研究更多方法。 对特定领域数据集进行预训练和微调等方法使 LLMs 能够推理并生成特定领域语言。 然而&#…...

HarmonyOS—UI 开发性能提升的推荐方法
开发者若使用低性能的代码实现功能场景可能不会影响应用的正常运行,但却会对应用的性能造成负面影响。本章节列举出了一些可提升性能的场景供开发者参考,以避免应用实现上带来的性能劣化。 使用数据懒加载 开发者在使用长列表时,如果直接采用…...

84 CTF夺旗-PHP弱类型异或取反序列化RCE
目录 案例1:PHP-相关总结知识点-后期复现案例2:PHP-弱类型对比绕过测试-常考点案例3:PHP-正则preg_match绕过-常考点案例4:PHP-命令执行RCE变异绕过-常考点案例5:PHP-反序列化考题分析构造复现-常考点涉及资源…...
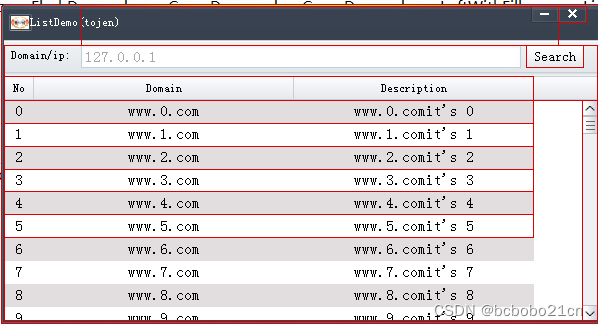
Duilib List 控件学习
这是自带的一个示例; 一开始运行的时候List中是空的,点击Search按钮以后就填充列表框; 先看一下列表框列头是在xml文件中形成的; <List name="domainlist" bkcolor="#FFFFFFFF" ... menu="true"> <ListHeader height="24…...

详细了解Node.js的配置与使用!
详细了解Node.js的配置与使用! Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。它允许开发者在服务器端运行 JavaScript,从而实现全栈 JavaScript 开发。本文将介绍 Node.js 的配置和 npm 的应用。 一、Node.js 配置 下载与安装 首先&…...

OpenCV 移动最小二乘图像变形
文章目录 一、简介二、实现代码三、实现效果参考文献一、简介 在现实生活中,我们常常应用一些刚性的变换来实现物体的旋转平移,对于非刚性的变换我们都没有在意,其实这种变换也是无处不在的,如我们经常看的动画就可以通过一些非刚性的变换达到一些非常夸张的效果。这里,我…...

【深度学习】S2 数学基础 P4 概率论
目录 基本概率论概率论公理随机变量 多个随机变量联合概率条件概率贝叶斯定理求和法则独立性 期望与方差小结 基本概率论 机器学习本质上,就是做出预测。而概率论提供了一种量化和表达不确定性水平的方法,可以帮助我们量化对某个结果的确定性程度。 在…...

跟我学c++中级篇——静态多态
一、多态 Polymorphism,多态。学习过c的人如果不知道多态,基本上就是打入c内部的C程序员了。在前边曾经对多态进行过分析,对其中的虚函数(虚表等)也进行过较为详细的说明。 多态其实非常好理解,不要硬扣书…...
)
设计模式--桥接模式(Bridge Pattern)
桥接模式(Bridge Pattern)是一种结构型设计模式,它主要是用于将抽象部分与实现部分分离,使它们可以独立地变化。 桥接模式主要包含以下几个角色: Abstraction(抽象类):定义抽象类的…...
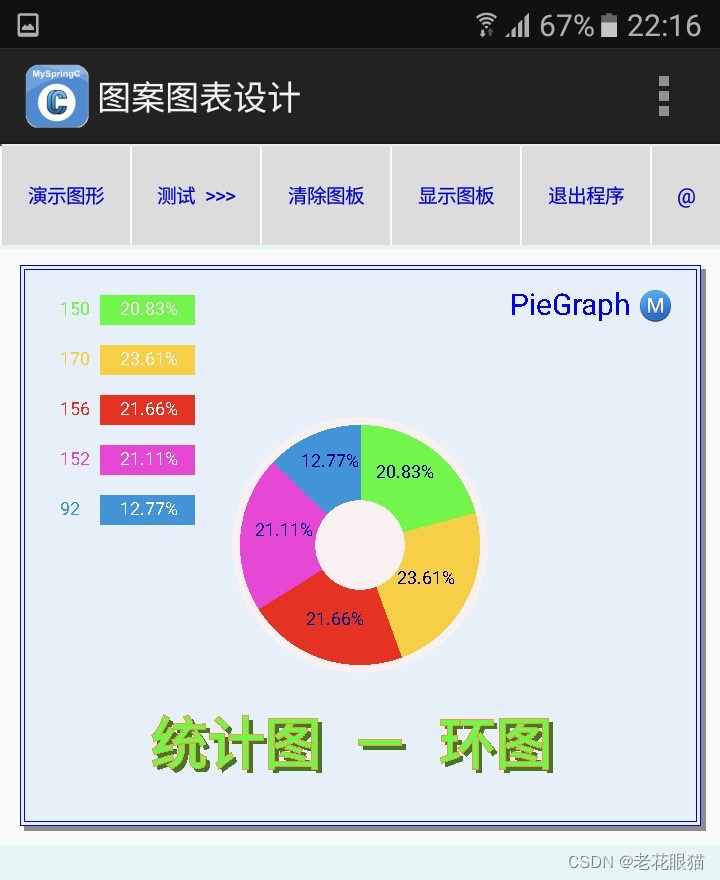
统计图饼图绘制方法(C语言)
统计图饼图绘制方法(C语言) 常用的统计图有条形图、柱形图、折线图、曲线图、饼图、环形图、扇形图。 前几类图比较容易绘制,饼图绘制较难。今值此介绍饼图的绘制方法。 本方法采用C语言的最基本功能: ( 1.)…...

洛谷C++简单题小练习day12—寻找最小值小程序
day12--寻找最小值--2.16 习题概述 题目描述 给出 n 和 n 个整数 ai,求这 n 个整数中最小值是什么。 输入格式 第一行输入一个正整数 n,表示数字个数。 第二行输入 n 个非负整数,表示 1,2…a1,a2…an,以空格隔开。 …...

相机图像质量研究(13)常见问题总结:光学结构对成像的影响--鬼影
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...
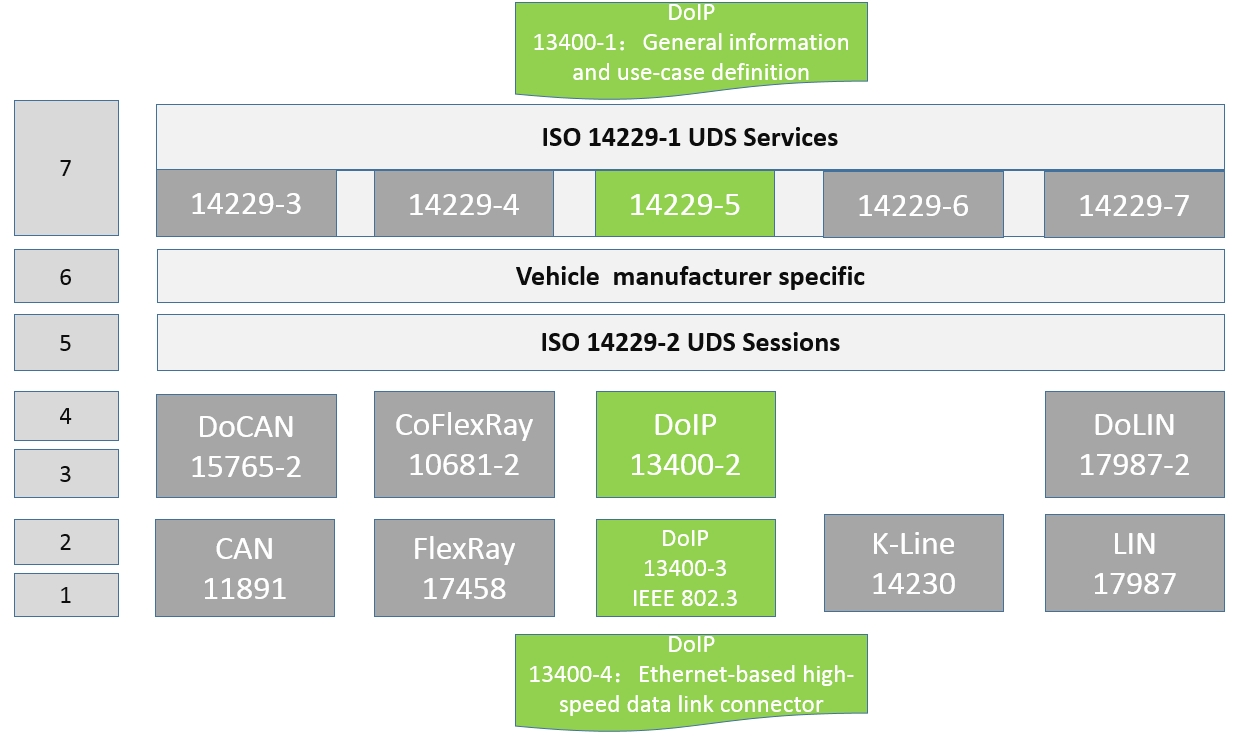
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师(Wechat:gongkenan2013)。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自己。江湖一碗茶,…...

掘根宝典之C++包含对象的类,私有继承,保护继承,三大继承方式总结
包含对象成员的类 包含,组合和层次化:一个类里面的类成员之一是个类对象 我们来看个例子 #include<iostream> using namespace std; class AA { private:int a_; public:AA(int a):a_(a){}void A(){cout << a_ << endl;} }; class …...

第六篇:MySQL图形化管理工具
经过前五篇的学习,对于数据库这门技术的理解,我们已经在心中建立了一个城堡大致的雏形,通过命令行窗口(cmd)快速上手了【SQL语法-DDL-数据定义语言】等相关命令 道阻且长,数据库技术这一宝藏中还有数不清的…...

计算机网络——12DNS
DNS DNS的必要性 IP地址标识主机、路由器但IP地址不好记忆,不便于人类用使用(没有意义)人类一般倾向于使用一些有意义的字符串来标识Internet上的设备存在着“字符串”——IP地址的转换的必要性人类用户提供要访问机器的“字符串”名称由DN…...
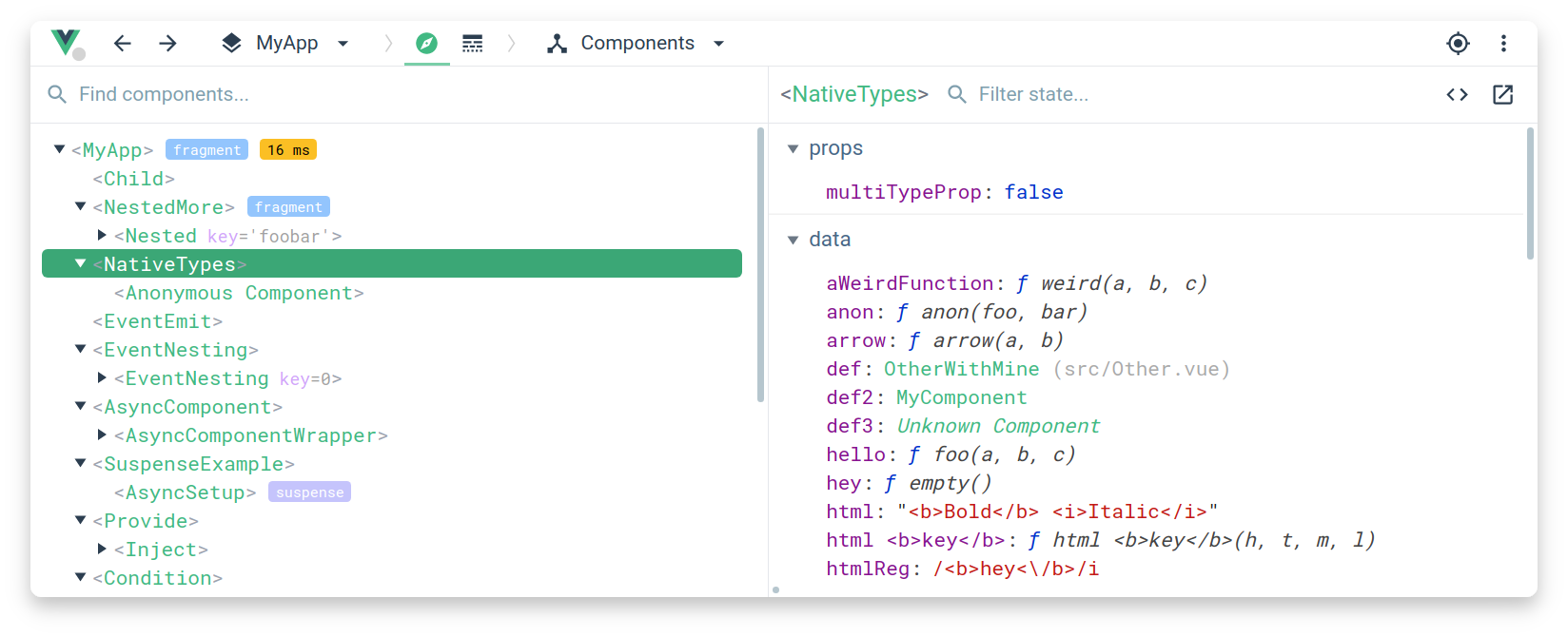
vue3-应用规模化-工具链
工具链 项目脚手架 Vite Vite 是一个轻量级的、速度极快的构建工具,对 Vue SFC 提供第一优先级支持。作者是尤雨溪,同时也是 Vue 的作者! 要使用 Vite 来创建一个 Vue 项目,非常简单: (推荐)…...
EasyExcel动态列导出
测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/tree/master/src/test/java/com/xiaobai/easyexcel/dynamiccolumn 官方文档:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 一、实现方式 1、根据需要导出的列…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
