Matplotlib plt.plot数据可视化应用案例
Matplotlib 是 Python 中一个非常流行的绘图库,它允许用户创建各种静态、动态、交互式的图表和可视化。plt.plot() 是 Matplotlib 中用于绘制二维数据的基本函数。
下面是一个使用 plt.plot() 的简单数据可视化应用案例:
案例:绘制正弦和余弦曲线
-
准备数据:首先,我们需要准备一些数据点来绘制正弦和余弦曲线。
-
绘制图形:使用
plt.plot()绘制正弦和余弦曲线。 -
添加标题和标签:为了使图形更具可读性,我们将添加标题、x轴和y轴标签。
-
显示图形:使用
plt.show()显示图形。
python复制代码
import numpy as np | |
import matplotlib.pyplot as plt | |
# 准备数据 | |
x = np.linspace(0, 4 * np.pi, 1000) # 生成从0到4π的1000个等间隔点 | |
y_sin = np.sin(x) # 计算这些点的正弦值 | |
y_cos = np.cos(x) # 计算这些点的余弦值 | |
# 绘制图形 | |
plt.figure(figsize=(8, 6)) # 设置图形大小 | |
plt.plot(x, y_sin, label='sin(x)') # 绘制正弦曲线并添加标签 | |
plt.plot(x, y_cos, label='cos(x)') # 绘制余弦曲线并添加标签 | |
# 添加标题和标签 | |
plt.title('Sine and Cosine Curves') # 添加标题 | |
plt.xlabel('x') # 添加x轴标签 | |
plt.ylabel('y') # 添加y轴标签 | |
plt.legend() # 显示图例 | |
# 显示图形 | |
plt.grid(True) # 添加网格线 | |
plt.show() # 显示图形 |
这个案例展示了如何使用 Matplotlib 的 plt.plot() 函数来绘制简单的二维曲线。你可以根据需要调整数据、颜色、样式等参数来创建各种自定义的图表。
相关文章:

Matplotlib plt.plot数据可视化应用案例
Matplotlib 是 Python 中一个非常流行的绘图库,它允许用户创建各种静态、动态、交互式的图表和可视化。plt.plot() 是 Matplotlib 中用于绘制二维数据的基本函数。 下面是一个使用 plt.plot() 的简单数据可视化应用案例: 案例:绘制正弦和余…...

ES实战--集群扩展
查看ES集群状态: GET /_cluster/health?prettytrue当一个节点加入集群的时候,ES会自动地尝试将分片在所有节点上进行均匀分配. 如果更多的节点加入集群,ES将试图在所有节点上均匀分配分片数量.这样每一个新加入的节点都能通过部分数据来分担负载 第二个节点发现第一个节点,并…...

【重要】django默认生成的表的意思记录
accounts_userprofile: 这是与用户相关的个人资料表,通常包含用户的额外信息,比如头像、个人描述等。 accounts_userprofile_groups: 这是用户个人资料和用户组之间的关联表,用于记录用户属于哪些用户组。 accounts_userprofile_user_permiss…...

12.3 OpenGL顶点后处理:平面着色
平面着色 Flatshading Flat shading (平面着色)是一种简化渲染技术,它在光栅化阶段将一个图元(primitive)的所有顶点赋予相同的颜色或其它输出变量的值。这些赋予的值来自于该图元的“引发顶点”(provoking vertex)。…...

实验5-6 使用函数判断完全平方数
本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare( int n ); 其中n是用户传入的参数,在长整型范围内。如果n是完全平方数,则函数IsSquare必须返回1,否则返回0。 裁判测试程序样例࿱…...

AI 或许真的能助力中产阶级重塑辉煌 [译]
原文:AI Could Actually Help Rebuild The Middle Class 作者:DAVID AUTOR 译文:AI 或许真的能助力中产阶级重塑辉煌 作者:宝玉 人工智能(AI)并不一定会夺走我们的工作。相反,它为我们提供了一个…...
C#利用接口实现选择不同的语种
目录 一、涉及到的知识点 1.接口定义 2.接口具有的特征 3.接口通过类继承来实现 4.有效使用接口进行组件编程 5.Encoding.GetBytes(String)方法 (1)检查给定字符串中是否包含中文字符 (2)编码和还原前后 6.Encoding.GetS…...

设计模式-适配器模式 Adapter
适配器模式 (Adapter) (重点) 适配器设计模式(Adapter Design Pattern)是一种结构型设计模式,用于解决两个不兼容接口之间的问题。适配器允许将一个类的接口转换为客户端期望的另一个接口,使得原本由于接口不兼容而不能一起工作的…...

算法训练day29Leetcode491递增子序列46全排列47全排列Ⅱ
491 递增子序列 题目描述 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一…...

内网穿透与搭建私人服务器
前言 内网穿透是一种技术,允许用户从外部网络访问内部私有网络中的服务器或设备。这对于想要从任何地方访问家中或办公室内部网络资源的用户非常有用。以下是为初学者准备的关于如何实现内网穿透以及搭建自己的私人服务器的详细指南。 在这个数字化时代,…...

交大论文下载器
原作者地址: https://github.com/olixu/SJTU_Thesis_Crawler 问题: http://thesis.lib.sjtu.edu.cn/的学位论文下载系统,该版权保护系统用起来很不方便,加载起来非常慢,所以该下载器实现将网页上的每一页的图片合并…...
)
全栈笔记_浏览器扩展篇(manifest.json文件介绍)
manifest.json介绍 是web扩展技术必不可少的插件配置文件,放在根目录作用: 指定插件的基本信息 name:名称manifest_version:manifest.json文件的版本号,可以写2或3version:版本description:描述定义插件的行为: browser_action:添加一个操作按钮到浏览器工具栏,点击按…...
)
蓝桥杯每日一题(python)
##斐波那契数列的应用 --- 题目斐波那契 题目: 如果数组 A (a0, a1, , an−1) 满足以下条件,就说它是一个斐波那契数组: 1. n ≥ 2; 2. a0 a1; 3. 对于所有的 i(i ≥ 2),都满足 ai ai−1 ai−2…...

【Vue】工程化开发脚手架Vue CLI
📝个人主页:五敷有你 🔥系列专栏:Vue⛺️稳重求进,晒太阳 工程化开发&脚手架Vue CLI 基本介绍 Vue Cli是Vue官方提供的一个全局命令工具 可以帮助我们快速创建一个开发Vue项目的标准化基础架子【集成了we…...

嵌入式培训机构四个月实训课程笔记(完整版)-Linux ARM驱动编程第三天-ARM Linux ADC和触摸屏开发 (物联技术666)
链接:https://pan.baidu.com/s/1V0E9IHSoLbpiWJsncmFgdA?pwd1688 提取码:1688 教学内容: 1、ADC S3C2440的A/D转换器包含一个8通道的模拟输入转换器,可以将模拟输入信号转换成10位数字编码。 在A/D转换时钟频率为2.5MHz时&…...
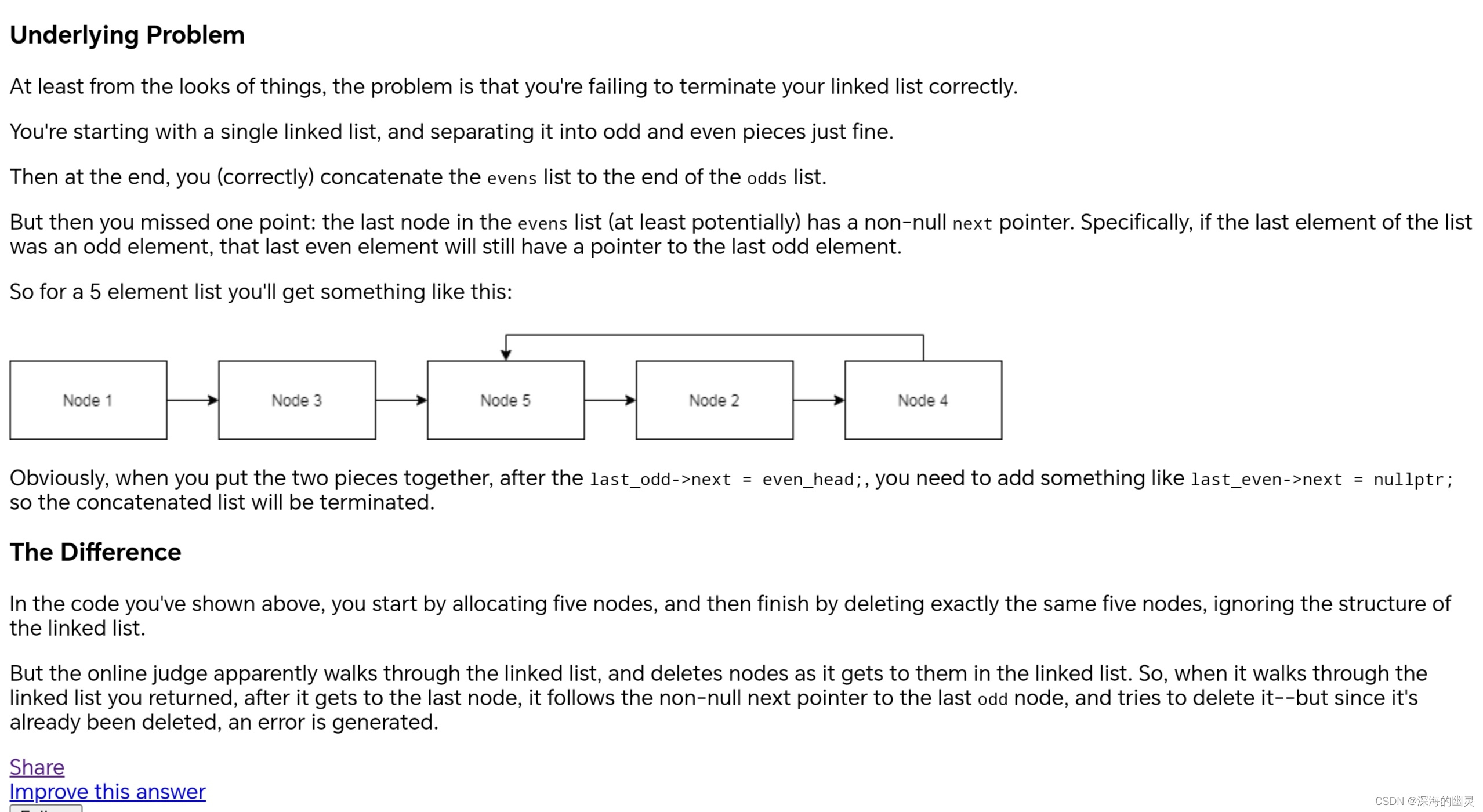
LeetCode “AddressSanitizer:heat-use-after-free on address“问题解决方法
heat-use-after-free : 访问堆上已经被释放的内存地址 现象:同样代码在LeetCode上报错,但是自己在IDE手动打印并不会报错 个人猜测,这个bug可能来源于LeetCode后台输出打印链表的代码逻辑问题。 问题描述 题目来自LeetCode的8…...

幸运彩票
L1-6 幸运彩票 分数 15 作者 陈越 单位 浙江大学 彩票的号码有 6 位数字,若一张彩票的前 3 位上的数之和等于后 3 位上的数之和,则称这张彩票是幸运的。本题就请你判断…...

搭建yum仓库服务器
安装 1.安装linux 1.1安装依赖 yum -y install gcc zlib zlib-devel pcre-devel openssl openssl-devel 1.2下载 cd /opt/nginx wget http://nginx.org/download/nginx-1.25.3.tar.gz 1.3解压 tar -xvf nginx-1.25.3.tar.gz 1.4配置 cd nginx-1.25.3 ./configure --pre…...

贪心算法练习day1
练习1--翻硬币 1)题目及要求 2)解题思路 输入的是字符串,要想将两组字符串进行一一对比,需要将字符串转换成字符数组,再使用for循环依次遍历字符数组,进行比对。 输入两行字符串,转换成两个字…...
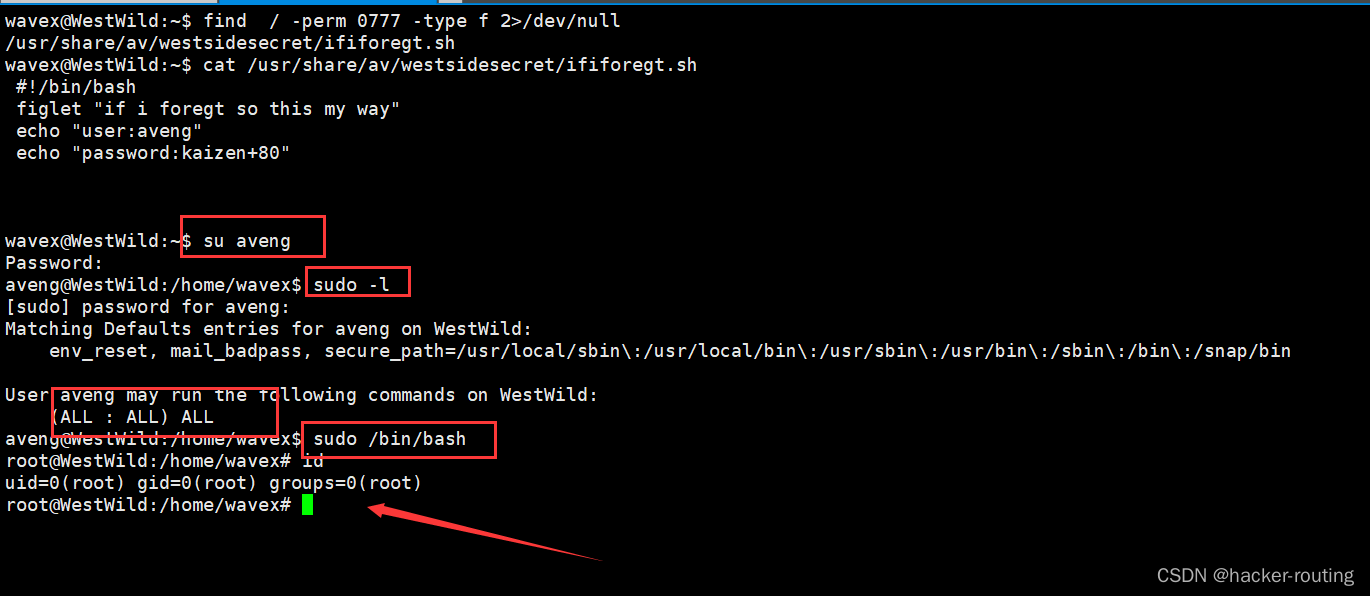
[VulnHub靶机渗透] WestWild 1.1
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【python】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
