C语言——oj刷题——杨氏矩阵
目录
1. 理解杨氏矩形的特点
2. 实现杨氏矩形查找算法
3. 编写示例代码
当我们谈到杨氏矩形时,我们指的是一种在二维数组中查找目标元素的高效算法。它是由杨氏(Yan Shi)教授提出的,因此得名为杨氏矩形。
杨氏矩形问题的场景是这样的:给定一个有序的二维数组,每一行从左到右递增,每一列从上到下递增。我们需要在这个二维数组中快速查找某个目标元素是否存在。
为了更好地理解和解决这个问题,我们将分为以下几个步骤进行讲解和编码示例:
- 理解杨氏矩形的特点
- 实现杨氏矩形查找算法
- 编写示例代码
1. 理解杨氏矩形的特点
杨氏矩形的特点是每一行从左到右递增,每一列从上到下递增。这意味着我们可以通过比较目标元素和当前元素的值来缩小查找范围。
具体来说,我们可以从矩形的右上角开始查找。如果目标元素比当前元素大,则目标元素必然不在当前元素的同一行,因此可以排除当前元素所在的行;如果目标元素比当前元素小,则目标元素必然不在当前元素的同一列,因此可以排除当前元素所在的列。通过这种方式,我们可以逐步缩小查找范围,直到找到目标元素或查找范围为空。
2. 实现杨氏矩形查找算法
基于上述特点,我们可以设计一个高效的杨氏矩形查找算法,具体步骤如下:
- 初始化当前元素为矩形的右上角元素
- 循环执行以下步骤:
- 如果当前元素等于目标元素,则返回找到目标元素的位置
- 如果目标元素比当前元素大,则将当前元素下移一行
- 如果目标元素比当前元素小,则将当前元素左移一列
- 如果循环结束仍未找到目标元素,则返回未找到的结果
3. 编写示例代码
下面是一个使用C语言编写的示例代码,演示如何实现杨氏矩形查找算法:
#include <stdio.h>
#include <stdbool.h>bool yangsMatrixSearch(int matrix[3][3], int target) {int rows = 3; // 矩阵的行数int cols = 3; // 矩阵的列数// 初始化当前元素为矩阵的右上角元素int row = 0;int col = cols - 1;// 循环查找while (row < rows && col >= 0) {if (matrix[row][col] == target) {return true; // 找到目标元素} else if (matrix[row][col] < target) {row++; // 目标元素比当前元素大,下移一行} else {col--; // 目标元素比当前元素小,左移一列}}return false; // 未找到目标元素
}int main() {int matrix[3][3] = {{1, 4, 7},{2, 5, 8},{3, 6, 9}};int target = 5;bool found = yangsMatrixSearch(matrix, target);if (found) {printf("目标元素 %d 存在于矩阵中\n", target);} else {printf("目标元素 %d 不存在于矩阵中\n", target);}return 0;
}在上述示例代码中,我们定义了一个yangsMatrixSearch函数,该函数接受一个二维数组(矩阵)和目标元素作为参数。函数内部实现了杨氏矩形查找算法。
在main函数中,我们定义了一个3x3的矩阵和一个目标元素。然后,调用yangsMatrixSearch函数来查找目标元素是否存在于矩阵中,并根据查找结果打印相应的信息。
希望这篇博客能够帮助你理解杨氏矩形问题,并提供了详细的讲解和代码示例。如果有任何疑问,请随时向我提问。
相关文章:

C语言——oj刷题——杨氏矩阵
目录 1. 理解杨氏矩形的特点 2. 实现杨氏矩形查找算法 3. 编写示例代码 当我们谈到杨氏矩形时,我们指的是一种在二维数组中查找目标元素的高效算法。它是由杨氏(Yan Shi)教授提出的,因此得名为杨氏矩形。 杨氏矩形问题的场景是…...

C++ 50道面试题
1. static关键字 1.全局static变量 存储位置:静态存储区,在程序运行期间一直存在 初始化: 未手动初始化的变量自动初始化为0 作用域: 从定义之处开始,到文件结束,仅能在本文件中使用 2.局部static变量…...

寒假学习记录14:JS字符串
目录 查找字符串中的特定元素 String.indexOf() (返回索引值) 截取字符串的一部分 .substring() (不影响原数组)(不允许负值) 截取字符串的一部分 .slice() (不影响原数…...

【数学建模】【2024年】【第40届】【MCM/ICM】【C题 网球运动中的“动量”】【解题思路】
一、题目 (一) 赛题原文 2024 MCM Problem C: Momentum in Tennis In the 2023 Wimbledon Gentlemen’s final, 20-year-old Spanish rising star Carlos Alcaraz defeated 36-year-old Novak Djokovic. The loss was Djokovic’s first at Wimbledon…...
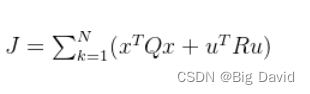
无人驾驶LQR控制算法 c++ 实现
参考博客: (1)LQR的理解与运用 第一期——理解篇 (2)线性二次型调节器(LQR)原理详解 (3)LQR控制基本原理(包括Riccati方程具体推导过程) (4)【基础…...
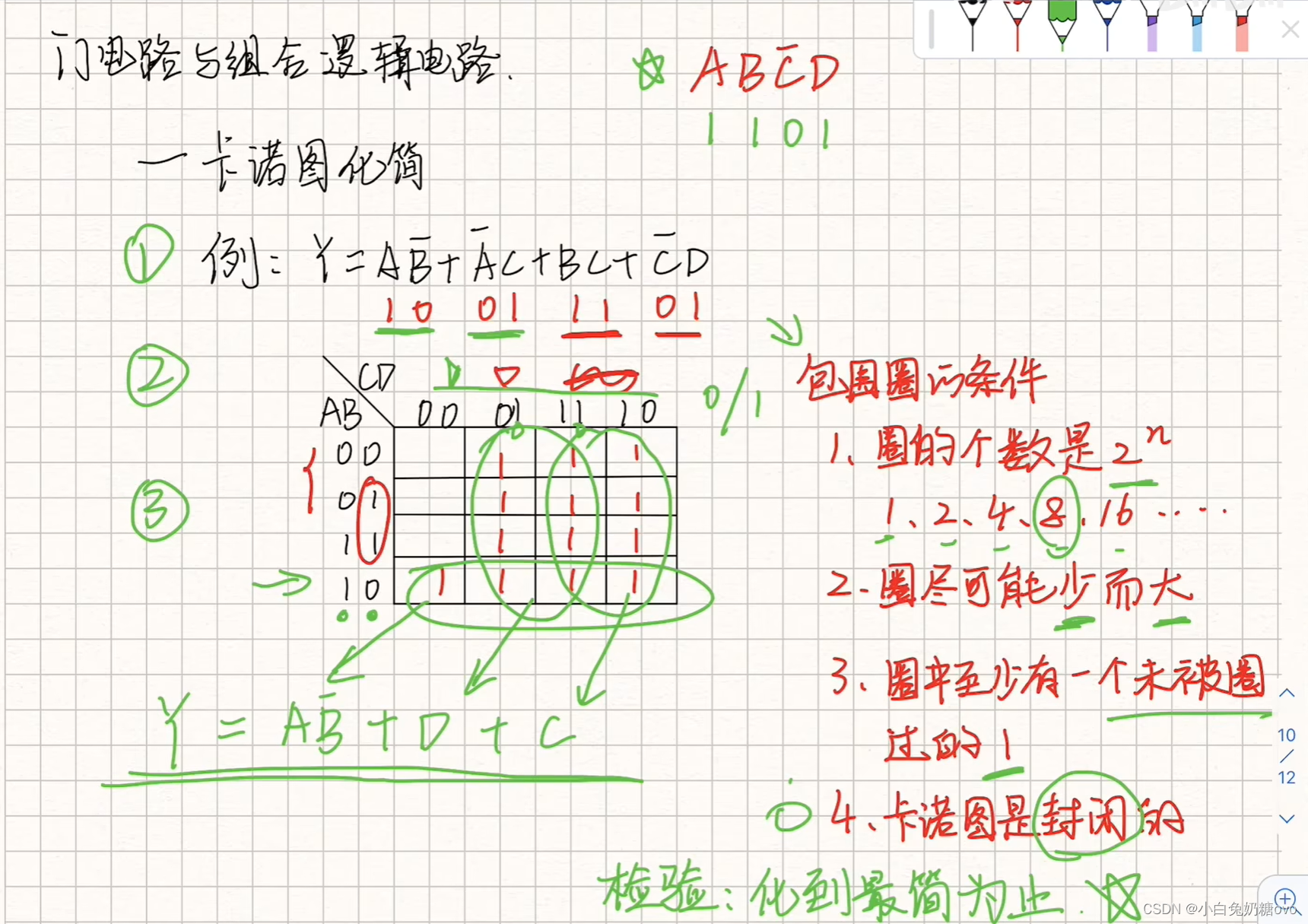
Karnaugh map (卡诺图)
【Leetcode】 289. Game of Life According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.” The board is made up of an m x n grid of cells, wh…...

C# CAD 框选pdf输出
在C#中进行AutoCAD二次开发时,实现框选(窗口选择)实体并输出这些实体到PDF文件通常涉及以下步骤: public ObjectIdCollection GetSelectedEntities() {using (var acTrans HostApplicationServices.WorkingDatabase.Transaction…...

【Linux】 Linux 小项目—— 进度条
进度条 基础知识1 \r && \n2 行缓冲区3 函数介绍 进度条实现版本 1代码实现运行效果 版本2 Thanks♪(・ω・)ノ谢谢阅读!!!下一篇文章见!!! 基础知识 1 \r &&a…...
Sora和Pika,RunwayMl,Stable Video对比!网友:Sora真王者,其他都是弟
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,所以创建了“AI信息Gap”这个公众号,专注于分享AI全维度知识…...

Go内存优化与垃圾收集
Go提供了自动化的内存管理机制,但在某些情况下需要更精细的微调从而避免发生OOM错误。本文介绍了如何通过微调GOGC和GOMEMLIMIT在性能和内存效率之间取得平衡,并尽量避免OOM的产生。原文: Memory Optimization and Garbage Collector Management in Go 本…...

【Spring】Bean 的生命周期
一、Bean 的生命周期 Spring 其实就是一个管理 Bean 对象的工厂,它负责对象的创建,对象的销毁等 所谓的生命周期就是:对象从创建开始到最终销毁的整个过程 什么时候创建 Bean 对象?创建 Bean 对象的前后会调用什么方法…...
云计算基础-存储基础
存储概念 什么是存储: 存储就是根据不同的应用程序环境,通过采取合理、安全、有效的方式将数据保存到某些介质上,并能保证有效的访问,存储的本质是记录信息的载体。 存储的特性: 数据临时或长期驻留的物理介质需要保…...
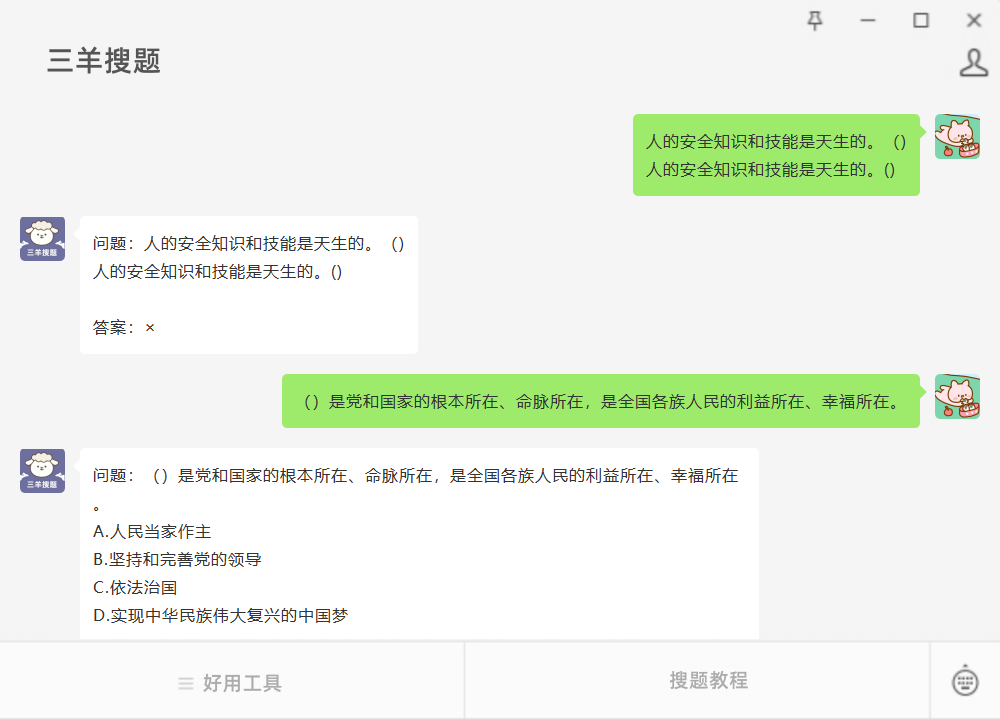
问题:人的安全知识和技能是天生的。() #媒体#知识分享#学习方法
问题:人的安全知识和技能是天生的。() 人的安全知识和技能是天生的。() 参考答案如图所示 问题:()是党和国家的根本所在、命脉所在,是全国各族人民的利益所在、幸福所在。 A.人民当家作主 B.坚持和完善…...
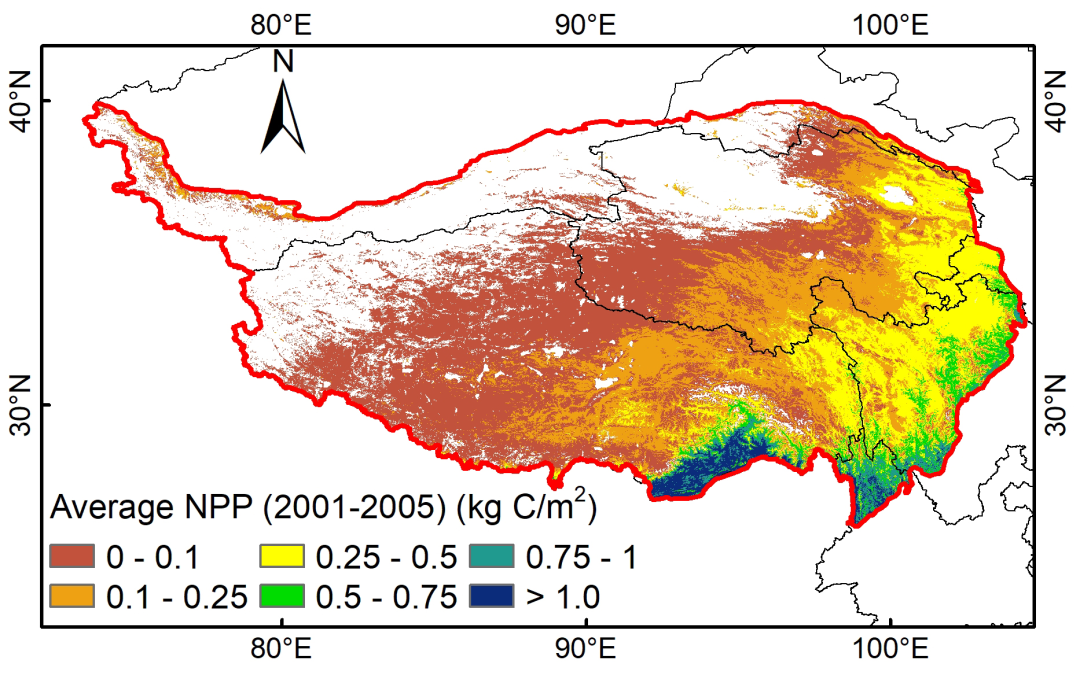
【数据分享】2001~2020年青藏高原植被净初级生产力数据集
各位同学们好,今天和大伙儿分享的是2001~2020年青藏高原植被净初级生产力数据集。如果大家有下载处理数据等方面的问题,您可以私信或评论。 朱军涛. (2022). 青藏高原植被净初级生产力数据集(2001-2020). 国家青藏高原数据中心. …...

【Spring MVC篇】返回响应
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【Spring MVC】 本专栏旨在分享学习Spring MVC的一点学习心得,欢迎大家在评论区交流讨论💌 目录 一、返回静态页面…...
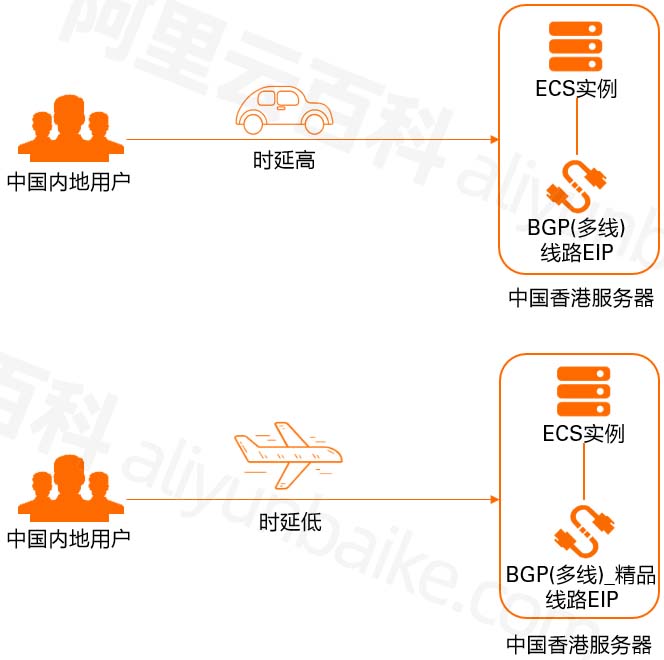
阿里云BGP多线精品EIP香港CN2线路低时延,价格贵
阿里云香港等地域服务器的网络线路类型可以选择BGP(多线)和 BGP(多线)精品,普通的BGP多线和精品有什么区别?BGP(多线)适用于香港本地、香港和海外之间的互联网访问。使用BGP…...
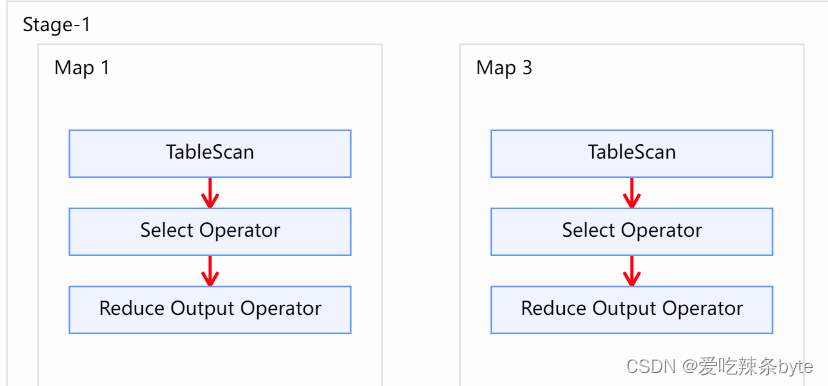
(08)Hive——Join连接、谓词下推
前言 Hive-3.1.2版本支持6种join语法。分别是:inner join(内连接)、left join(左连接)、right join(右连接)、full outer join(全外连接)、left semi join(左…...

创新技巧|迁移到 Google Analytics 4 时如何保存历史 Universal Analytics 数据
Google Universal Analytics 从 2023 年 7 月起停止收集数据(除了付费 GA360 之外)。它被Google Analytics 4取代。为此,不少用户疑惑:是否可以将累积(历史)数据从 Google Analytics Universal 传输到 Goog…...

一个小而实用的 Python 包 pangu,实现在中文和半宽字符(字母、数字和符号)之间自动插入空格
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一个小巧的库,可以避免自己重新开发功能。利用 Python 包 pangu,可以轻松实现在 CJK(中文、日文、韩文)和半宽字符(字母、数字和符号…...

openJudge | 中位数 C语言
总时间限制: 2000ms 内存限制: 65536kB 描述 中位数定义:一组数据按从小到大的顺序依次排列,处在中间位置的一个数或最中间两个数据的平均值(如果这组数的个数为奇数,则中位数为位于中间位置的那个数;如果这组数的个…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...
