蓝桥杯每日一题------背包问题(四)
前言
前面讲的都是背包的基础问题,这一节我们进行背包问题的实战,题目来源于一位朋友的询问,其实在这之前很少有题目是我自己独立做的,我一般习惯于先看题解,验证了题解提供的代码是正确的后,再去研究题解,这就给我自己养成了一种依赖的习惯。我害怕自己去挑战没有答案的问题,朋友问的这道题来源于一个小众网站,因此没有题解,出于试一试的态度,我也算比较轻松的做出来了,让我十分有满足感,十分感谢他。但是他好久之前问我的一道题,我现在还没有回他(sorry)。话不多说看题目吧。
数的分解
题目描述
把 A 分解成 B 个各不相同的正整数之和,并且要求每个正整数都不包含数字
2和4,一共有多少种不同的分解方法?注意交换几个整数的顺序被视为同一种方法,例如 1000+1001+18 和 1001+1000+18被视为同一种。
输入描述
第一行包一个整数 T,表示测试数据的规模。接下来 T 行每行 2 个整数A,B。
输出描述
对每个输入输出一个整数表示答案。
输入数据
2
10 2
2019 3
输出数据
2
40785
评测用例规模与约定
对于所有评测用例,1≤T≤10,1≤A≤2500,1≤B≤10。
这道题目类似于蓝桥杯的一道真题,那道真题是分解数字2019,可以去看一下,数的分解。因为那个题目只分解一个数字,所以采用dfs甚至for循环枚举都可以过。但是这道题目是分解好几个数字,而且分解后数字的个数也不是固定的,如果用dfs会超时。
那么试着考虑一下动态规划,因为无法为它划分为区间,状压,期望,树形,所以只能是普通的dp,那就用普通的dp的思考顺序进行思考。
定义dp数组
第一步:缩小规模。 考虑分解成B个整数,那么我用B当作数据规模。
第二步:限制。 需要记录当前B个数字之和是多少。除了这一个限制还有什么限制呢?选出来的数字不能包含2或4,这一个限制好考虑,只需要在选择的时候检查一遍就可以了。还有呢?还有需要保证选择的方案不会重复,这种限制最常见的是用a<b<c来约束,即后一个一定比前一个大,这样相当于规定了选择的顺序,但是如果是这样的话我需要知道前一个选择的是啥,这个时候就需要记录。其它限制应该没有了。
第三步:写出dp数组。 dp[i][j][k]表示当前选择了i个数字,所选数字之和为j且最后一个选择的数字是k时的?。这样要求啥?求方案数啊,一般求啥表示啥(也有特殊情况),所以‘?’表示的是方案数。
第四步:推状态转移方程。 dp[i][j][k]应该从哪里转移过来呢,必然是从前i-1个数字的状态转移,这个状态还应该考虑此时j和k的情况,当前可以选择的数字必然是比j小,比k大,假设当前选择的数字是p,则 k < p < j k<p<j k<p<j。所以 d p [ i ] [ j ] [ p ] + = d p [ i − 1 ] [ j − p ] [ k ] dp[i][j][p] += dp[i-1][j-p][k] dp[i][j][p]+=dp[i−1][j−p][k]
综上状态转移方程如下
d p [ i ] [ j ] [ p ] + = d p [ i − 1 ] [ j − p ] [ k ] dp[i][j][p] += dp[i-1][j-p][k] dp[i][j][p]+=dp[i−1][j−p][k]
考虑写代码了
第一步:确定好遍历顺序。 对于背包问题,一般第一个for遍历规模,第二个for遍历限制。但是我们的限制有两个,所以加上规模一共三层嵌套的for循环。
第二步:确定好转移位置。 对于当前可以选择的数字,只要比k大我都可以尝试在这一步选择,所以需要一个for循环遍历此时转移的数字。综上一共4层嵌套的for循环。那么代码如下
int dp[][][] = new int[k+1][n+1][n+1];//n表示要分解的数字,k表示分解后的数字个数// TODO Auto-generated method stubfor(int i = 1;i <= n;i++) dp[1][i][i] = 1;for(int i = 1;i <= k;i++) {//10 遍历规模for(int j = 1;j <= n;j++) {//2500 遍历限制 for(int q = 1;q <= j;q++) {//if(check(q)) continue;//检查是否包含了2或4for(int p = q+1;p <= j;p++) {if(check(p)) continue;dp[i][j][p] += dp[i-1][j-p][q]; }}}}
可以算一下上述思路的时间复杂度是 O ( k ∗ n ∗ n ∗ n ) = 10 ∗ 2500 ∗ 2500 ∗ 2500 > 1 e 8 O(k*n*n*n)=10*2500*2500*2500>1e8 O(k∗n∗n∗n)=10∗2500∗2500∗2500>1e8,会超时。那么在写上述思路的过程中你有没有发现一个问题。对于n范围内的数字我只有可能会选择一次,选择k个数字,并且数字之和恰好等于n,这像不像二维01背包问题?没错就是!按照刚刚所想重新思考dp数组。
定义dp数组
第一步:缩小规模。 对于n范围内的数字我只有可能会选择一次,小于n的所有数字都可以看作是一个物品,一共有n个物品。
第二步:限制。
限制1:选出来的数字不能包含2或4,这一个限制好考虑,只需要在选择的时候检查一遍就可以了,不需要新的维度。
限制2:选出来的数字个数不能超过B,需要一个维度来限制。
限制3:选出来的数字之和不能超过n,需要一个维度来限制。
第三步:写出dp数组。 dp[i][j][k]表示当前选择了i个数字,所选数字之和为k所选数字个数为j时的方案数。
第四步:推状态转移方程。 dp[i][j][k]应该从哪里转移过来呢,必然是从前i-1个数字的状态转移,如果第i个数字不选,则 dp[i][j][k]+= dp[i-1][j][k],如果选择第i个数字,则 dp[i][j][k]+= dp[i-1][j-1][k-i]
综上状态转移方程如下
i f ( k > i ) if(k>i) if(k>i) d p [ i ] [ j ] [ p ] = d p [ i − 1 ] [ j ] [ k ] + d p [ i − 1 ] [ j − 1 ] [ k − i ] dp[i][j][p] = dp[i-1][j][k]+dp[i-1][j-1][k-i] dp[i][j][p]=dp[i−1][j][k]+dp[i−1][j−1][k−i]
e l s e else else d p [ i ] [ j ] [ p ] = d p [ i − 1 ] [ j ] [ k ] dp[i][j][p] = dp[i-1][j][k] dp[i][j][p]=dp[i−1][j][k]
考虑写代码了
第一步:确定好遍历顺序。 对于背包问题,一般第一个for遍历规模,第二个for遍历限制。但是我们的限制有两个,所以加上规模一共三层嵌套的for循环。
第二步:确定好转移位置。 当前第i个数字进行转移,所以不需要额外的for循环,代码如下
import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;
public class Main{static int n,k,ans=0;//检查是不是带有2 或 4static Boolean check(int parm) {while(parm>0) {int t=parm%10;if(t==2 || t==4) return true;parm/=10;}return false;}
public static void main(String[] args) {
// f();Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();long dp[][][] = new long[2500+1][10+1][2500+1];//当前考虑的物品,当前选择的物品个数,当前选择的物品的重量,当前物品选还是没选while(t-- > 0) {n=scanner.nextInt();k = scanner.nextInt();int sum=0;//从2500个物品里,选10个物品,且价值恰好为n dp[0][0][0]=1;for(int i = 1;i <= n;i++) {dp[i][1][i] = 1; dp[i][0][0] = 1;
// dp[1][0][0][0] = 1;}for(int i = 1;i <= n;i++) {//for(int j = 1;j <= k;j++) {//for(int q = 1;q <= n;q++) {//if(check(i)) {dp[i][j][q] = dp[i-1][j][q];}else {if(q >= i)dp[i][j][q] = dp[i-1][j-1][q-i]+dp[i-1][j][q];elsedp[i][j][q] = dp[i-1][j][q];}
// System.out.println(dp[i][j][q] + " " + i + " " + j + " " + q);}}}long ans = 0;ans = dp[n][k][n]; System.out.println(ans);}
}
}
此时的时间复杂度是 O ( B ∗ A ∗ A ) = 10 ∗ 2500 ∗ 2500 = 62500000 < 1 e 8 O(B*A*A)=10*2500*2500=62500000<1e8 O(B∗A∗A)=10∗2500∗2500=62500000<1e8,貌似可以,但是别忘了还有T,所以时间复杂度应该是 O ( B ∗ A ∗ A ∗ T ) = 10 ∗ 2500 ∗ 2500 ∗ 10 = 62500000 > 1 e 8 O(B*A*A*T)=10*2500*2500*10=62500000>1e8 O(B∗A∗A∗T)=10∗2500∗2500∗10=62500000>1e8,但是我们可以看到当n=2500,t=1时是不超时的,而对于其它的n<2500和k<=10,其实可以直接用dp[n][k][n]来表示,所以我们只需要预处理出n=2500和k=10的情况,然后针对其它样例直接输出就可以了。
超时的问题解决了,还有一个问题,不太常遇到的问题,空间超限,因为我们设的数组是三维的,空间大小将近1e9了。这里可以考虑用滚动dp来节省空间,滚动dp在背包问题(一)中进行过讲解,修改后的代码如下,
import java.util.Arrays;
import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;public class Main{static int n,k,ans=0;//检查是不是带有2 或 4static Boolean check(int parm) {while(parm>0) {int t=parm%10;if(t==2 || t==4) return true;parm/=10;}return false;}
public static void main(String[] args) {
// f();Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();long dp[][][] = new long[2][10+1][2500+1];//当前考虑的物品,当前选择的物品个数,当前选择的物品的重量,当前物品选还是没选dp[0][0][0] = 1;dp[1][1][1] = 1;dp[1][0][0] = 1;n = 2500;k = 10;for(int i = 1;i <= n;i++) {//for(int j = 1;j <= k;j++) {//for(int q = 1;q <= n;q++) {// if(check(i)) {dp[i&1][j][q] = dp[(i-1)&1][j][q];}else {if(q >= i)dp[i&1][j][q] = dp[(i-1)&1][j-1][q-i]+dp[(i-1)&1][j][q];elsedp[i&1][j][q] = dp[(i-1)&1][j][q];}
// System.out.println(dp[i][j][q] + " " + i + " " + j + " " + q);}}}while(t-- > 0) {n=scanner.nextInt();k = scanner.nextInt();long ans = 0;ans = dp[n&1][k][n]; System.out.println(ans);}
}
}
这个网站的题目应该是对蓝桥杯题目进行了改编,不得不说改编的质量还是挺高的,再来另一个类似的题目
数的分解2
题目描述
将 N 拆分成 M 个正整数之和,总共有多少种拆分方法?注意交换顺序视为不同的方法,例如 2025 = 1000 + 1025 和 2025 = 1025 + 1000 就视为不同的方法。
输入描述
第一行包一个整数 T,表示测试数据的规模。接下来
T 行每行 2 个整数,N,M。
输出描述
对每个输入输出一个整数表示答案。由于答案可能会很大,请输出答案除以 109+7 的结果。
输入数据
2
40 5
1988 2
输出数据
82251
1987
评测用例规模与约定
对于所有评测用例,1≤T≤10,1≤N≤2500,1≤M≤10。
这道题和上一道题有什么区别呢?除了没有不能选包含2和4的数字的约数之外,还规定了不同的顺序视为不同的方案,这样就不是01背包了。因为对于01背包而言,10+11和11+10是一种方案。还是先按照dp的步骤考虑一下。
定义dp数组
第一步:缩小规模。 考虑分解成B个整数,那么我用B当作数据规模。
第二步:限制。 需要记录当前B个数字之和是多少。
第三步:写出dp数组。 dp[i][j]表示当前选择了i个数字,所选数字之和为j时的方案数。
第四步:推状态转移方程。 dp[i][j]应该从哪里转移过来呢,必然是从前i-1个数字的状态转移,这个状态还应该考虑此时j的情况,当前可以选择的数字必然是比j小,假设当前选择的数字是p,则 p < j p<j p<j。所以 d p [ i ] [ j ] + = d p [ i − 1 ] [ j − p ] dp[i][j] += dp[i-1][j-p] dp[i][j]+=dp[i−1][j−p]
综上状态转移方程如下
d p [ i ] [ j ] [ p ] + = d p [ i − 1 ] [ j − p ] dp[i][j][p] += dp[i-1][j-p] dp[i][j][p]+=dp[i−1][j−p]
考虑写代码了
第一步:确定好遍历顺序。 对于背包问题,一般第一个for遍历规模,第二个for遍历限制。
第二步:确定好转移位置。 对于当前可以选择的数字,只要比j小我都可以尝试在这一步选择,所以需要一个for循环遍历此时转移的数字。综上一共3层嵌套的for循环。那么代码如下
import java.util.Arrays;
import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;public class Main{static int n,k,ans=0;
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();n = 2500;k = 10;int mod = (int) (1e9+7);int dp[][] = new int[k+1][n+1];// TODO Auto-generated method stubfor(int i = 1;i <= n;i++) dp[1][i] = 1;for(int i = 1;i <= k;i++) {//10 遍历规模for(int j = 1;j <= n;j++) {//2500 遍历限制 for(int q = 1;q <= j;q++) {//dp[i][j] += dp[i-1][j-q]; dp[i][j] %= mod;}}}while(t-- > 0) {n=scanner.nextInt();k = scanner.nextInt();long ans = 0;ans = dp[k][n]; System.out.println(ans);}
}
该思路的时间复杂度是 O ( N ∗ M ∗ N ) = 2500 ∗ 2500 ∗ 10 < 1 e 8 O(N*M*N)=2500*2500*10<1e8 O(N∗M∗N)=2500∗2500∗10<1e8,可以通过本题。
可以看见同一个思路,因为限制的降低,dp数组维数降低,时间复杂度就降低了。
相关文章:
)
蓝桥杯每日一题------背包问题(四)
前言 前面讲的都是背包的基础问题,这一节我们进行背包问题的实战,题目来源于一位朋友的询问,其实在这之前很少有题目是我自己独立做的,我一般习惯于先看题解,验证了题解提供的代码是正确的后,再去研究题解…...

OpenAI发布Sora技术报告深度解读!真的太强了!
😎 作者介绍:我是程序员洲洲,一个热爱写作的非著名程序员。CSDN全栈优质领域创作者、华为云博客社区云享专家、阿里云博客社区专家博主、前后端开发、人工智能研究生。公粽号:洲与AI。 🎈 本文专栏:本文收录…...
AJAX——接口文档
1 接口文档 接口文档:描述接口的文章 接口:使用AJAX和服务器通讯时,使用的URL,请求方法,以及参数 传送门:AJAX阶段接口文档 <!DOCTYPE html> <html lang"en"><head><meta c…...

leetcode hot100不同路径
本题可以采用动态规划来解决。还是按照五部曲来做 确定dp数组:dp[i][j]表示走到(i,j)有多少种路径 确定递推公式:我们这里,只有两个移动方向,比如说我移动到(i,j&#x…...

【前端工程化面试题目】webpack 的热更新原理
可以在顺便学习一下 vite 的热更新原理,请参考这篇文章。 首先有几个知识点需要明确 热更新是针对开发过程中的开发服务器的,也就是 webpack-dev-serverwebpack 的热更新不需要额外的插件,但是需要在配置文件中 devServer属性中配置&#x…...
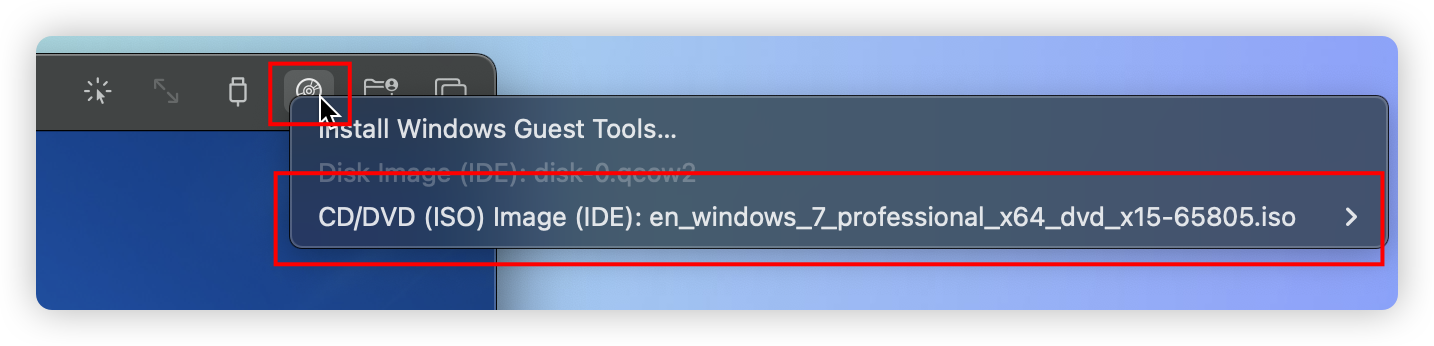
不花一分钱,在 Mac 上跑 Windows(M1/M2 版)
这是在 MacOS M1 上体验最新 Windows11 的效果: VMware Fusion,可以运行 Windows、Linux 系统,个人使用 licence 免费 安装流程见 👉 https://zhuanlan.zhihu.com/p/452412091 从申请 Fusion licence 到下载镜像,再到…...

Attempt to call an undefined function glutInit
Attempt to call an undefined function glutInit 解决方法: 从这里下载PyOpenGL 的whl安装文件, https://drive.google.com/drive/folders/1mz7faVsrp0e6IKCQh8MyZh-BcCqEGPwx 安装命令举栗 pip install PyOpenGL-3.1.7-cp39-cp39-win_amd64.whl pi…...
AB测试最小样本量
1.AB实验过程 常见的AB实验过程,分流-->实验-->数据分析-->决策:分流:用户被随机均匀的分为不同的组实验:同一组内的用户在实验期间使用相同的策略,不同组的用户使用相同或不同的策略。数据收集:…...

在Spring中事务失效的场景
在Spring框架中,事务管理是通过AOP(面向切面编程)实现的,主要依赖于Transactional注解。然而,在某些情况下,事务可能会失效。以下是一些可能导致Spring事务失效的常见场景: 非public方法&#…...

Rust 学习笔记 - 变量声明与使用
前言 任何一门编程语言几乎都脱离不了:变量、基本类型、函数、注释、循环、条件判断,这是一门编程语言的语法基础,只有当掌握这些基础语法及概念才能更好的学习 Rust。 变量介绍 Rust 是一种强类型语言,但在声明变量时…...
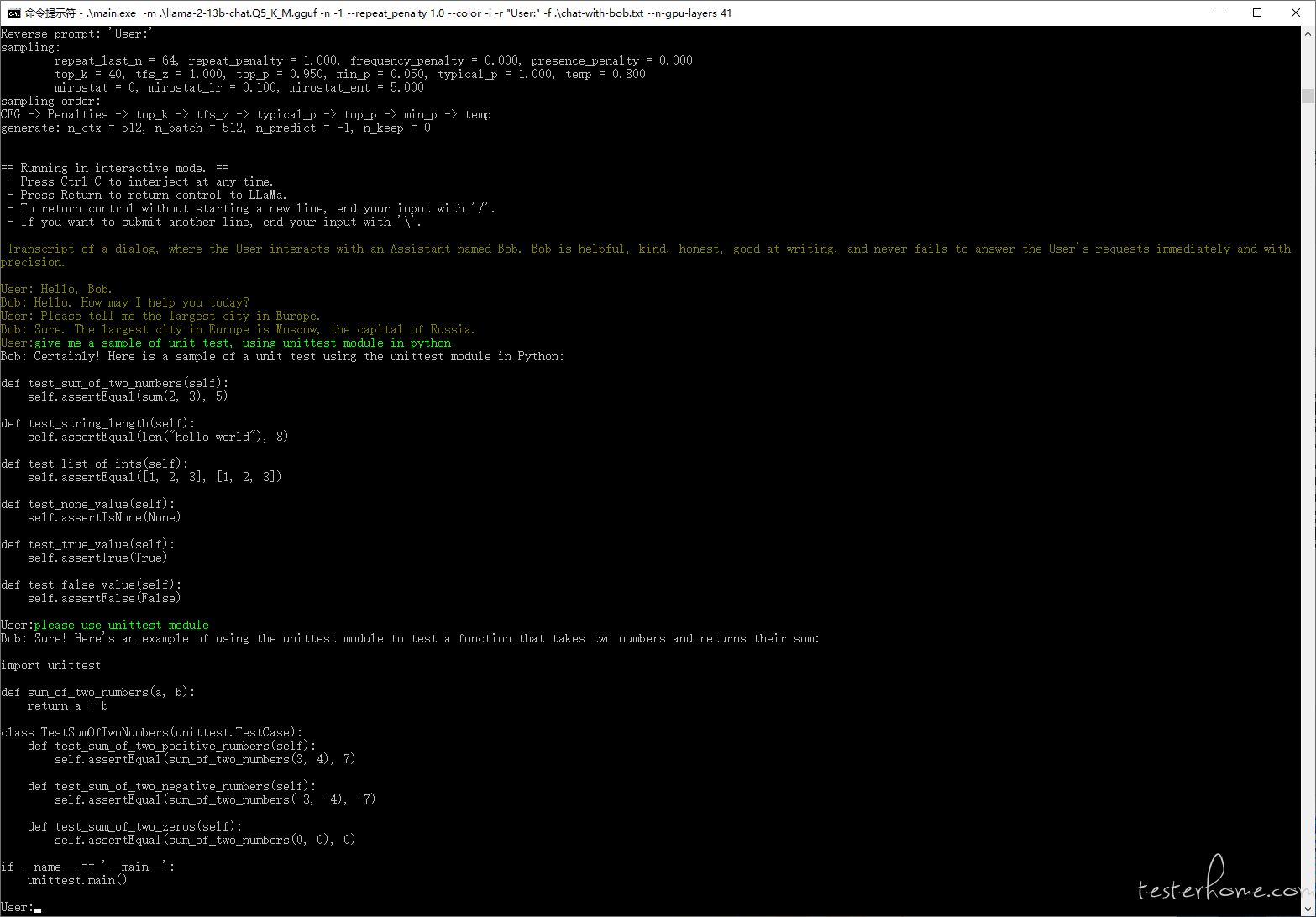
windows 下跑起大模型(llama)操作笔记
原贴地址:https://testerhome.com/topics/39091 前言 国内访问 chatgpt 太麻烦了,还是本地自己搭一个比较快,也方便后续修改微调啥的。 之前 llama 刚出来的时候在 mac 上试了下,也在 windows 上用 conda 折腾过,环…...
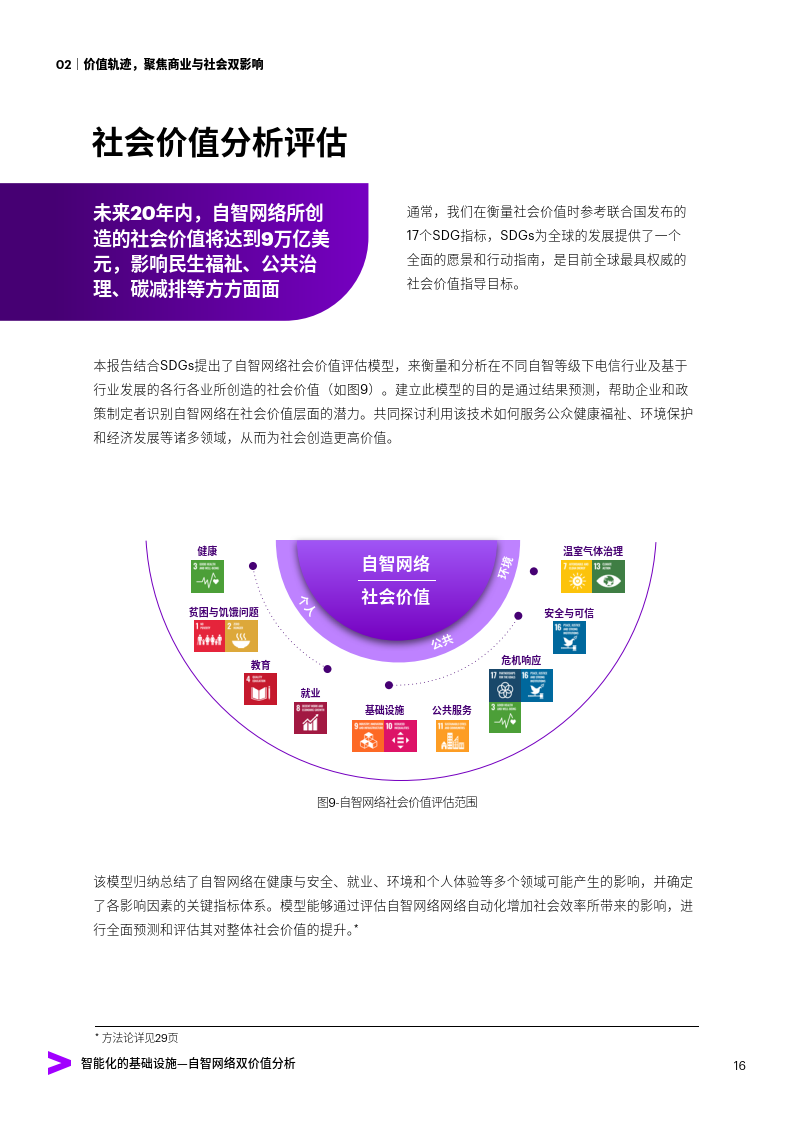
人工智能专题:基础设施行业智能化的基础设施,自智网络双价值分析
今天分享的是人工智能系列深度研究报告:《人工智能专题:基础设施行业智能化的基础设施,自智网络双价值分析》。 (报告出品方:埃森哲) 报告共计:32页 自智网络驱动的电信产业变革 经过多年的…...

docker 编译安装redis脚本
在Docker中编译安装Redis通常不是一个常见的做法,因为Redis官方提供了预编译的Docker镜像,这些镜像包含了已经编译好的Redis二进制文件。不过,如果你有特殊需求,想要自己从源代码编译Redis并打包成Docker镜像,你可以使…...
鸿蒙开发系列教程(二十三)--List 列表操作(2)
列表样式 1、设置内容间距 在列表项之间添加间距,可以使用space参数,主轴方向 List({ space: 10 }) { … } 2、添加分隔线 分隔线用来将界面元素隔开,使单个元素更加容易识别。 startMargin和endMargin属性分别用于设置分隔线距离列表侧…...
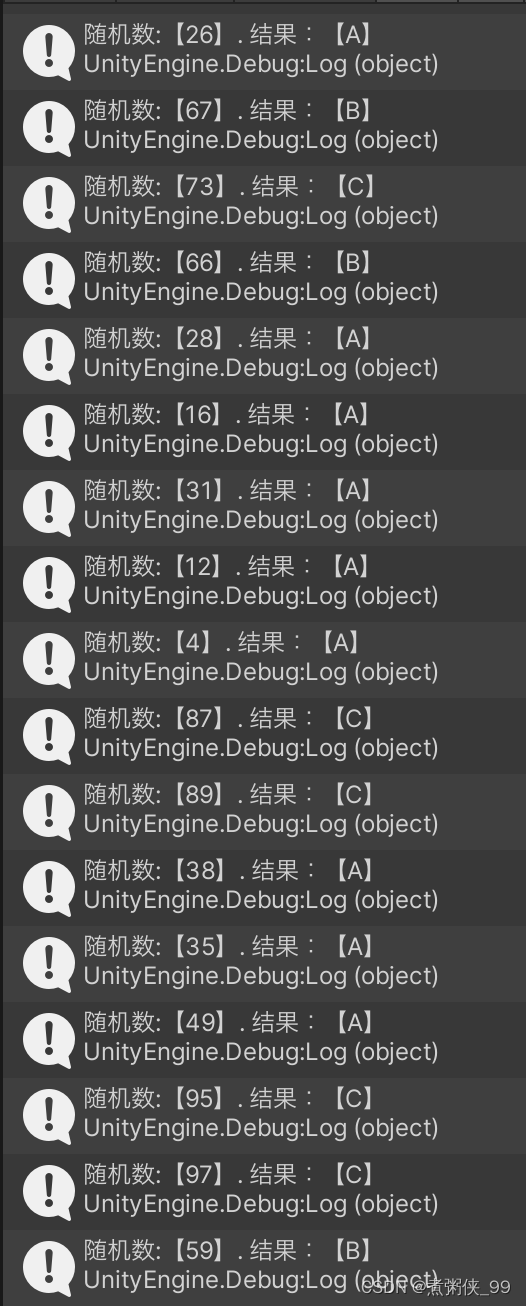
C#根据权重抽取随机数
(游戏中一个很常见的简单功能,比如抽卡抽奖抽道具,或者一个怪物有多种攻击动作,按不同的权重随机出个攻击动作等等……) 假如有三种物品 A、B、C,对应的权重分别是A(50),…...

SORA:OpenAI最新文本驱动视频生成大模型技术报告解读
Video generation models as world simulators:作为世界模拟器的视频生成模型 1、概览2、Turning visual data into patches:将视觉数据转换为补丁3、Video compression network:视频压缩网络4、Spacetime Latent Patches:时空潜在…...

阿里云第七代云服务器ECS计算c7、通用g7和内存r7配置如何选择?
阿里云服务器配置怎么选择合适?CPU内存、公网带宽和ECS实例规格怎么选择合适?阿里云服务器网aliyunfuwuqi.com建议根据实际使用场景选择,例如企业网站后台、自建数据库、企业OA、ERP等办公系统、线下IDC直接映射、高性能计算和大游戏并发&…...
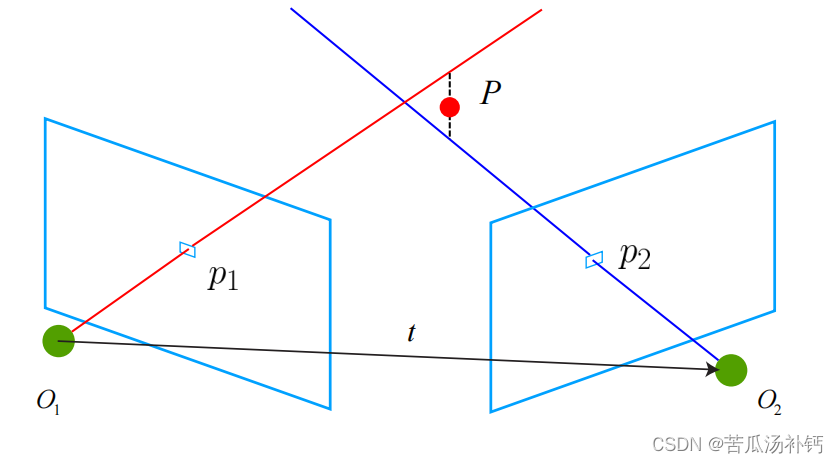
视觉slam十四讲学习笔记(六)视觉里程计 1
本文关注基于特征点方式的视觉里程计算法。将介绍什么是特征点,如何提取和匹配特征点,以及如何根据配对的特征点估计相机运动。 目录 前言 一、特征点法 1 特征点 2 ORB 特征 FAST 关键点 BRIEF 描述子 3 特征匹配 二、实践:特征提取…...
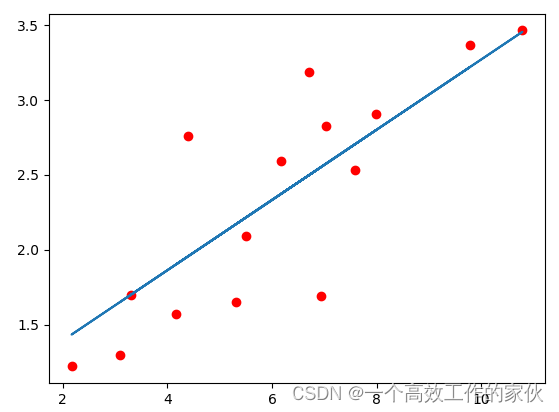
PyTorch-线性回归
已经进入大模微调的时代,但是学习pytorch,对后续学习rasa框架有一定帮助吧。 <!-- 给出一系列的点作为线性回归的数据,使用numpy来存储这些点。 --> x_train np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],[9.779], [6.1…...
C++数据结构与算法——栈与队列
C第二阶段——数据结构和算法,之前学过一点点数据结构,当时是基于Python来学习的,现在基于C查漏补缺,尤其是树的部分。这一部分计划一个月,主要利用代码随想录来学习,刷题使用力扣网站,不定时更…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
