AB测试最小样本量
1.AB实验过程
常见的AB实验过程,分流-->实验-->数据分析-->决策:
分流:用户被随机均匀的分为不同的组
实验:同一组内的用户在实验期间使用相同的策略,不同组的用户使用相同或不同的策略。
数据收集:日志根据实验系统为用户打标记,用于记录用户行为,然后数据计算系统根据带有实验标记的体制计算用户的各种实验数据指标。
数据分析和决策:实验者去理解和分析不同的策略对用户起了什么样的作用。
2.中心极限定理
将策略推全来验证策略效果是比较危险的,因此AB实验的对象是从总体当中去抽样数据,总体的分布可能会有多种形态,如正态分布、偏态分布、严重偏态分布等,总体的数据量也有多有少。‘
AB实验是用小样本去推断整体,这就会有一个问题:抽样的样本至少多少能保证统计的科学性?
样本均值的分布,趋近于正态分布,正态分布曲线由均值和方差决定,该分布均值的均值E( ̅x)趋近于总体均值u。就算总体分布不是正态分布,依然可以通过抽样得到样本均值的分布,近似正态分布,这样就可以使用正态分布来估计置信区间,从而实现参数检验(如t检验)
3. 样本容量
当每次从总体中抽样数据时,计算均值会得到一个数,抽样同样的数据量,计算均值,也会得到一个数,两个数大概率不会一样,因此,当抽样多次,计算的均值就会形成一个分布。
当总体分布是正态分布时,样本容量n为任意数,u的抽样分布都是正态分布
当总体非正态,如指数分布、均匀分布等,样本容量n>30, 近似为正态分布
当总体非正态,分布为严重偏态或有异常值,样本容量n>50,近似为正态分布
上文说的样本容量,即每个随机样本中个体的数量,用n表示,当按照样本量抽取多次的时候,才能得到正态分布,抽样的次数,叫样本量。E( ) = u 与样本容量无关,样本标准差
和样本容量有关(总体标准差=样本标准差/
),样本容量越大,样本标准差
越小。假设样本容量=总量,那最后就成一条线。
基于均值分布,就能计算出 在均值u附近一定举例的概率,反之根据概率,也可以得到置信区间。
4.最小样本量
在正态分布中置信区间为
为显著性水平,置信水平是1-
,
为标准正态概率分布上侧面积为
时的Z值,
为边际误差,边际误差的含义是在统计学中,业务人员主观上可以接受的误差范围。
总体均值u,样本均值 ̅x ,两者之间的误差ε,u = + ε
误差ε与边际误差存在对应关系。
指标主要有两种:均值类和比率类,有不同的边际误差计算方法。
均值类指标,计算得到
含义:在当前的方差水平下,要以1-的把握检测出边际误差不大于ε的变化,样本量至少需要n个。
从公式中可以看到,当边际误差减少为原来的时,所需的样本容量变为原来的4倍,是指数级关系。因此,在满足业务需求的情况下,尽量采用较大的边际误差,由于边际误差是业务需要检测的最低变化幅度,所以又称为最小样本量。
对比率类指标的方差计算与均值有所不同,方差=
,所以置信区间为:
方差可以使用经验值或者小样本抽取,还可以=0.5,这样得到的n是一个最大值,因为我们知道当
=0.5时,
能取到最大。
因此解出来的n为
相关文章:
AB测试最小样本量
1.AB实验过程 常见的AB实验过程,分流-->实验-->数据分析-->决策:分流:用户被随机均匀的分为不同的组实验:同一组内的用户在实验期间使用相同的策略,不同组的用户使用相同或不同的策略。数据收集:…...

在Spring中事务失效的场景
在Spring框架中,事务管理是通过AOP(面向切面编程)实现的,主要依赖于Transactional注解。然而,在某些情况下,事务可能会失效。以下是一些可能导致Spring事务失效的常见场景: 非public方法&#…...

Rust 学习笔记 - 变量声明与使用
前言 任何一门编程语言几乎都脱离不了:变量、基本类型、函数、注释、循环、条件判断,这是一门编程语言的语法基础,只有当掌握这些基础语法及概念才能更好的学习 Rust。 变量介绍 Rust 是一种强类型语言,但在声明变量时…...
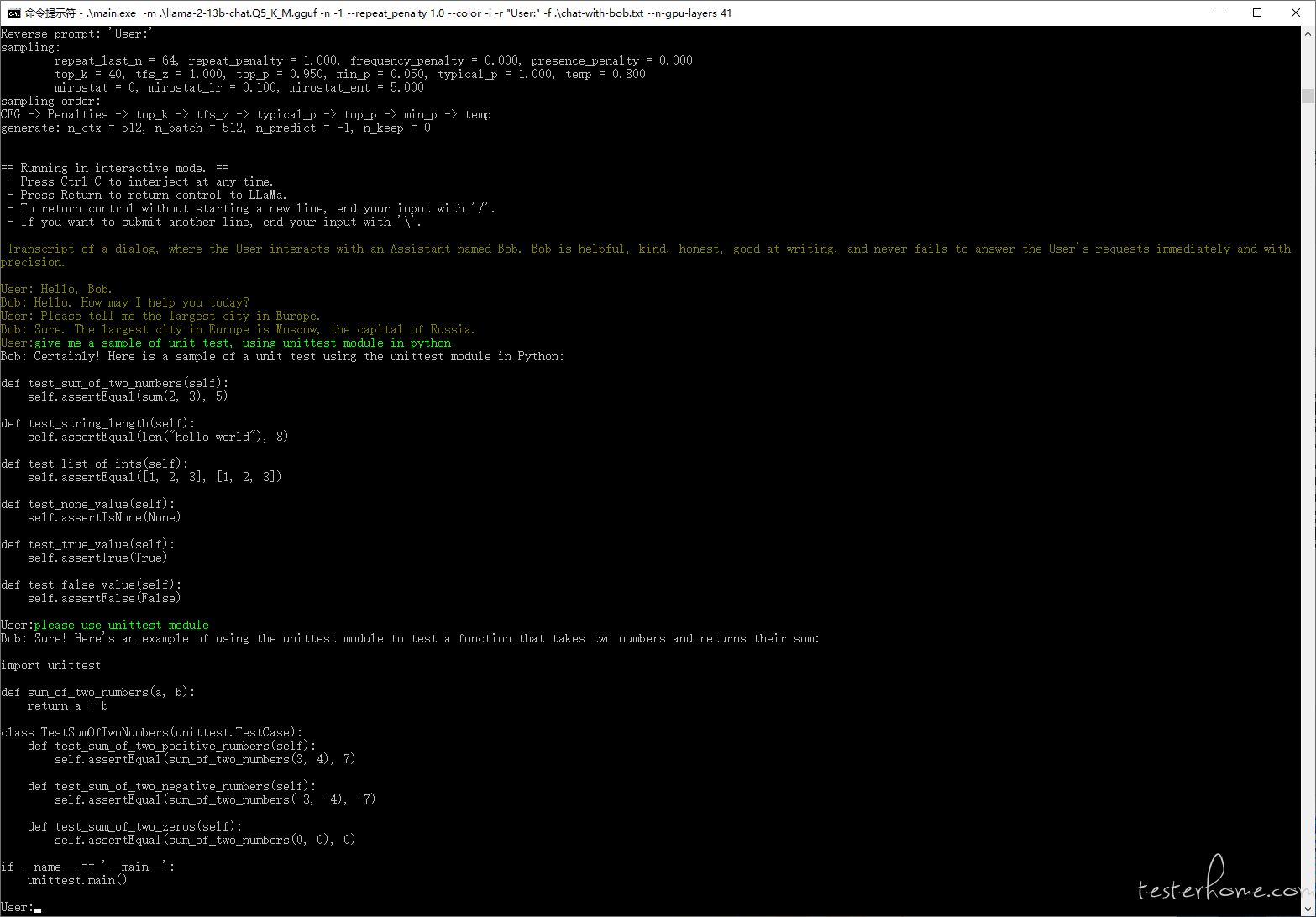
windows 下跑起大模型(llama)操作笔记
原贴地址:https://testerhome.com/topics/39091 前言 国内访问 chatgpt 太麻烦了,还是本地自己搭一个比较快,也方便后续修改微调啥的。 之前 llama 刚出来的时候在 mac 上试了下,也在 windows 上用 conda 折腾过,环…...
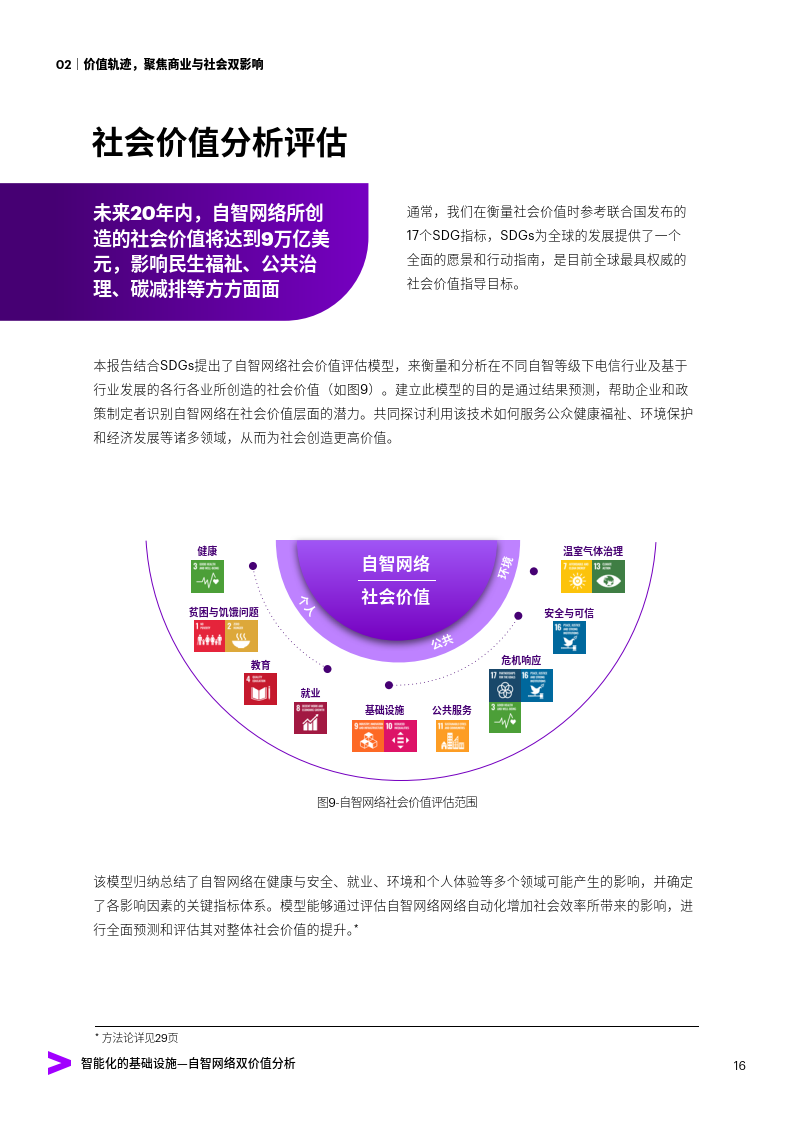
人工智能专题:基础设施行业智能化的基础设施,自智网络双价值分析
今天分享的是人工智能系列深度研究报告:《人工智能专题:基础设施行业智能化的基础设施,自智网络双价值分析》。 (报告出品方:埃森哲) 报告共计:32页 自智网络驱动的电信产业变革 经过多年的…...

docker 编译安装redis脚本
在Docker中编译安装Redis通常不是一个常见的做法,因为Redis官方提供了预编译的Docker镜像,这些镜像包含了已经编译好的Redis二进制文件。不过,如果你有特殊需求,想要自己从源代码编译Redis并打包成Docker镜像,你可以使…...
鸿蒙开发系列教程(二十三)--List 列表操作(2)
列表样式 1、设置内容间距 在列表项之间添加间距,可以使用space参数,主轴方向 List({ space: 10 }) { … } 2、添加分隔线 分隔线用来将界面元素隔开,使单个元素更加容易识别。 startMargin和endMargin属性分别用于设置分隔线距离列表侧…...
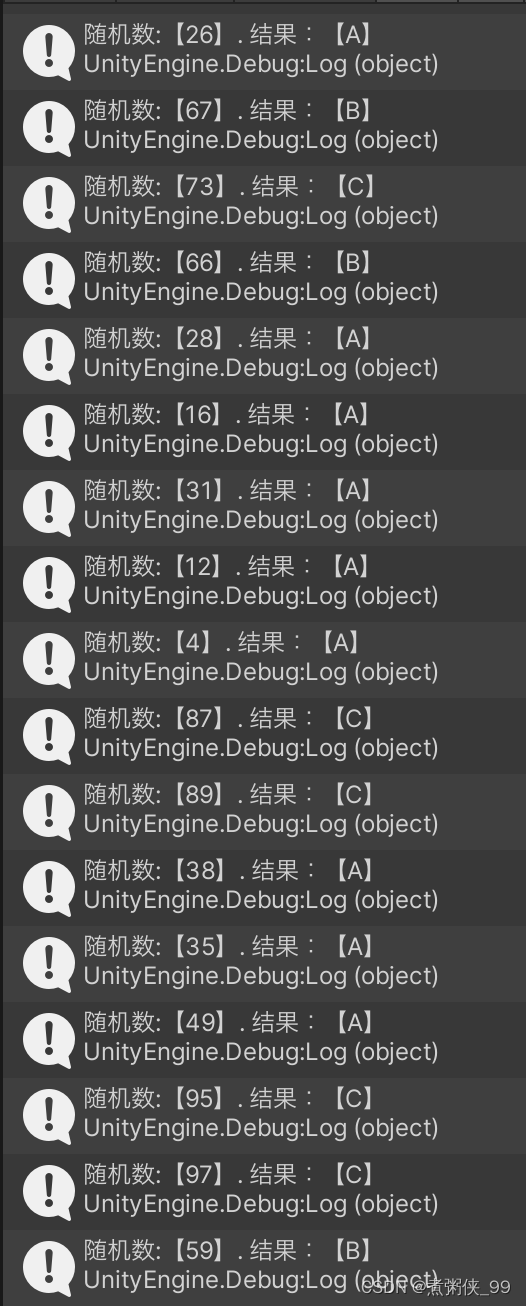
C#根据权重抽取随机数
(游戏中一个很常见的简单功能,比如抽卡抽奖抽道具,或者一个怪物有多种攻击动作,按不同的权重随机出个攻击动作等等……) 假如有三种物品 A、B、C,对应的权重分别是A(50),…...

SORA:OpenAI最新文本驱动视频生成大模型技术报告解读
Video generation models as world simulators:作为世界模拟器的视频生成模型 1、概览2、Turning visual data into patches:将视觉数据转换为补丁3、Video compression network:视频压缩网络4、Spacetime Latent Patches:时空潜在…...

阿里云第七代云服务器ECS计算c7、通用g7和内存r7配置如何选择?
阿里云服务器配置怎么选择合适?CPU内存、公网带宽和ECS实例规格怎么选择合适?阿里云服务器网aliyunfuwuqi.com建议根据实际使用场景选择,例如企业网站后台、自建数据库、企业OA、ERP等办公系统、线下IDC直接映射、高性能计算和大游戏并发&…...
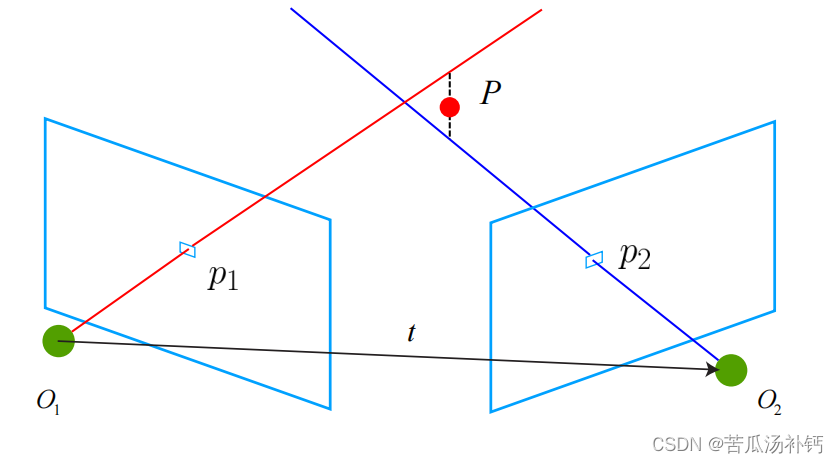
视觉slam十四讲学习笔记(六)视觉里程计 1
本文关注基于特征点方式的视觉里程计算法。将介绍什么是特征点,如何提取和匹配特征点,以及如何根据配对的特征点估计相机运动。 目录 前言 一、特征点法 1 特征点 2 ORB 特征 FAST 关键点 BRIEF 描述子 3 特征匹配 二、实践:特征提取…...
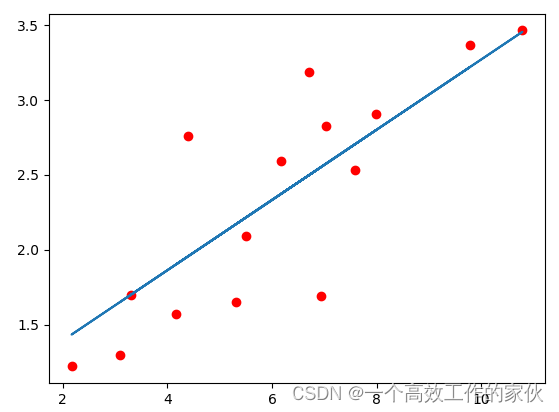
PyTorch-线性回归
已经进入大模微调的时代,但是学习pytorch,对后续学习rasa框架有一定帮助吧。 <!-- 给出一系列的点作为线性回归的数据,使用numpy来存储这些点。 --> x_train np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],[9.779], [6.1…...
C++数据结构与算法——栈与队列
C第二阶段——数据结构和算法,之前学过一点点数据结构,当时是基于Python来学习的,现在基于C查漏补缺,尤其是树的部分。这一部分计划一个月,主要利用代码随想录来学习,刷题使用力扣网站,不定时更…...
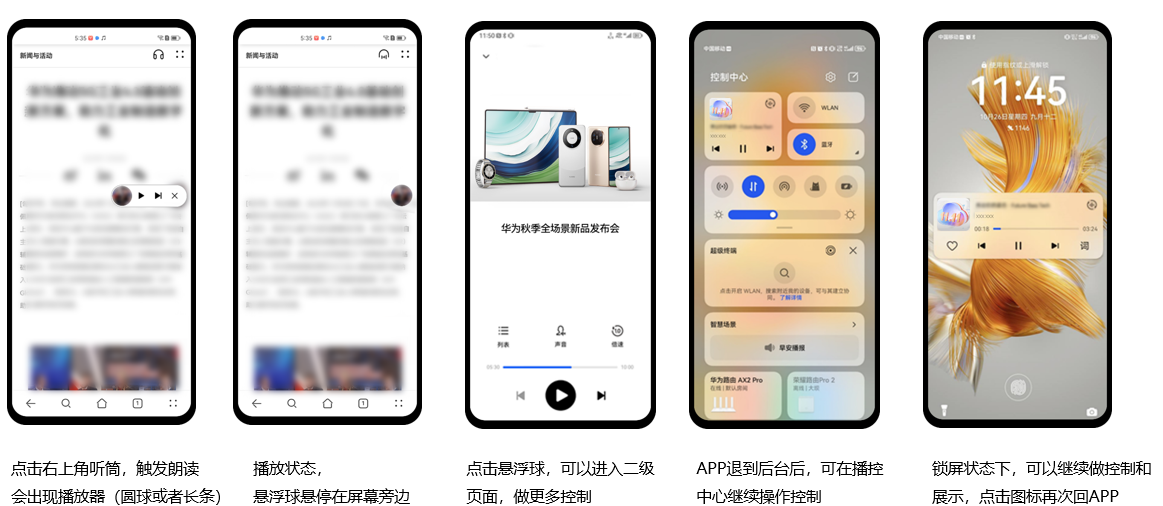
掌上新闻随心播控,HarmonyOS SDK助力新浪新闻打造精致易用的资讯服务新体验
原生智能是HarmonyOS NEXT的核心亮点之一,依托HarmonyOS SDK丰富全面的开放能力,开发者只需通过几行代码,即可快速实现AI功能。新浪新闻作为鸿蒙原生应用开发的先行者之一,从有声资讯入手,将基于Speech Kit朗读控件上线…...
2024年危险化学品经营单位主要负责人证模拟考试题库及危险化学品经营单位主要负责人理论考试试题
题库来源:安全生产模拟考试一点通公众号小程序 2024年危险化学品经营单位主要负责人证模拟考试题库及危险化学品经营单位主要负责人理论考试试题是由安全生产模拟考试一点通提供,危险化学品经营单位主要负责人证模拟考试题库是根据危险化学品经营单位主…...

C/C++如何把指针所指向的指针设为空指针?
实践出真知,指针对于初学的友友来说,头都要大了。喵喵一直遵循在实践中学,在学习中实践,相信你也会有所得! 以下是该问题的解决方案: int** ptrPtr new int*; // 创建指向指针的指针 int* ptr new int;…...
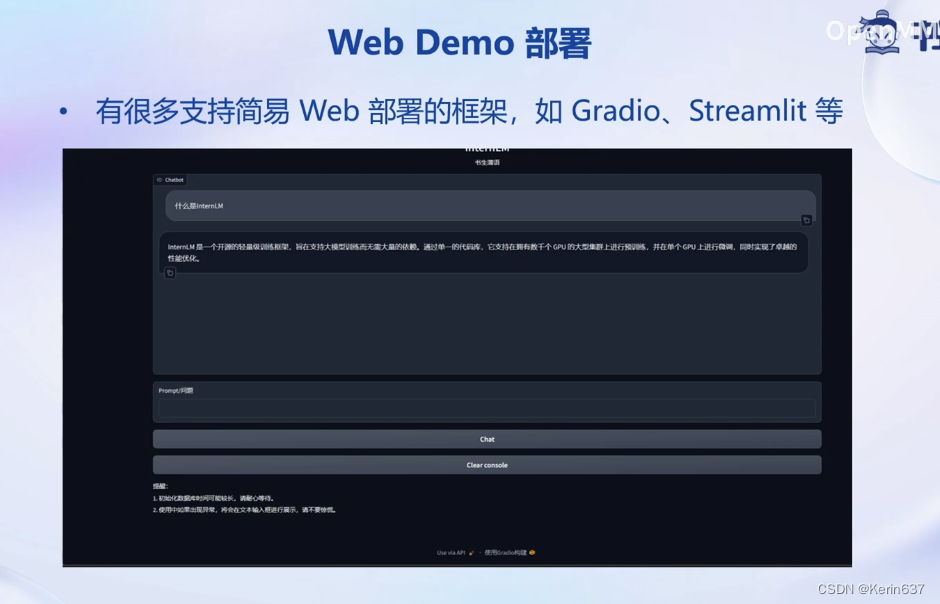
第三节:基于 InternLM 和 LangChain 搭建你的知识库(课程笔记)
视频链接:https://www.bilibili.com/video/BV1sT4y1p71V/?vd_source3bbd0d74033e31cbca9ee35e111ed3d1 文档地址: https://github.com/InternLM/tutorial/tree/main/langchain 课程笔记: 1.仅仅包含训练时间点之前的数据,无法…...
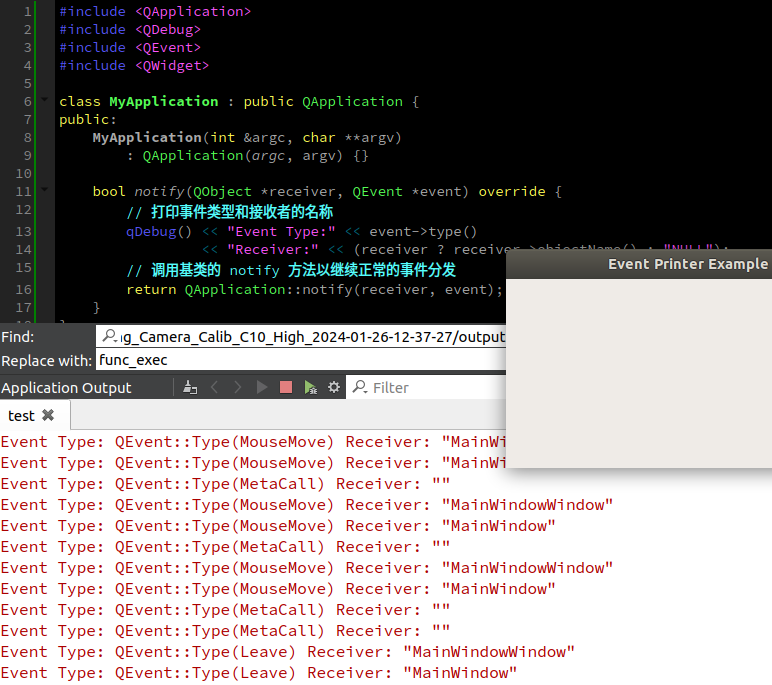
qt-C++笔记之打印所有发生的事件
qt-C笔记之打印所有发生的事件 code review! 文章目录 qt-C笔记之打印所有发生的事件1.ChatGPT问答使用 QApplication 的 notify 方法使用 QObject 的 event 方法 2.使用 QObject 的 event 方法3.使用 QApplication 的 notify 方法 1.ChatGPT问答 在Qt C中,若要打…...

pytorch 实现线性回归(深度学习)
一 查看原始函数 初始化 %matplotlib inline import random import torch from d2l import torch as d2l 1.1 生成原始数据 def synthetic_data(w, b, num_examples):x torch.normal(0, 1, (num_examples, len(w)))y torch.matmul(x, w) bprint(x:, x)print(y:, y)y tor…...
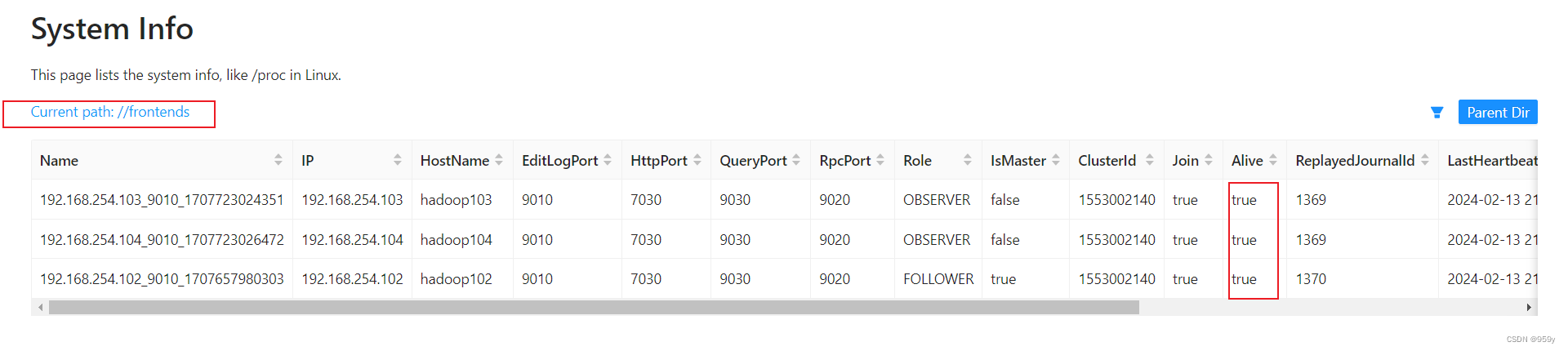
[Doris] Doris的安装和部署 (二)
文章目录 1.安装要求1.1 Linux操作系统要求1.2 软件需求1.3 注意事项1.4 内部端口 2.集群部署2.1 操作系统安装要求2.2 下载安装包2.3 解压2.4 配置FE2.5 配置BE2.6 添加BE2.7 FE 扩容和缩容2.8 Doris 集群群起脚本 3.图形化 1.安装要求 1.1 Linux操作系统要求 1.2 软件需求 1…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
